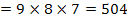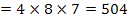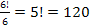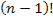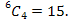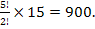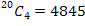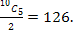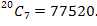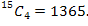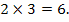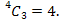How many do we each start with
How many do we each start with
Harry Potter Hogwarts Mystery Barnaby Lee Walkthrough
Guide for Year 3 Chapter 8 Harry Potter Hogwarts Mystery Barnaby Lee Walkthrough – You Know Who is defeated! (the boggart form, anyway) The information in your brother’s room now leads you to the library, which may conceal a Cursed Vault. 
Harry Potter: Hogwarts Mystery by Jam City, Inc. on iOS and Android devices
Harry Potter Hogwarts Mystery Year 3 Chapter 8 Walkthrough
There are a lot of task in year 3 chapter 8 :
1. Jacob’s notes hinted at a Cursed Vault being in the Hogwarts Library. Find it!
2. You need a plan to get into the Restricted Section and find the Cursed Vault. Ask Tulip.
3. Barnaby Lee can help you stay ahead of Merula. Persuade him to join your cause.
4. Barnaby wants you to prove your duelling prowess before he agrees to help you.
5. Barnaby wants to celebrate your new partnership with a Butterbeer.
There’s 1 Lesson to finish in order to finish this chapter :
Potion Class : Doxycide – a paralysing agent that stops obnoxious Doxies
Learning about Barnaby : Befriend Barnaby!
You’re going to think i’m mad…
o People say that about me
v I try not to judge
x I’m quick to judge
Our parents were Death Eaters…
o Your parents don’t define you
v That must have been hard…
x I hope they were punished
Just like You-Know-Who…
o You’re better than that
v Maybe he didn’t have a choice
x You’re supposed to say his name
Barnaby casts his Charms with brute force. His bullheadedness can clear any obstacle, and his knowledge of Slytherin could prove useful…
Here are the questions and answers for friendships if you hanging out with Barnaby :
Let’s join the Gobstones Club
o We founded the Gobstones Club
v Let’s drink Confusing Concoction
x Let’s appreciate the spimplicity
Wait until you see this move…
o I just saw it
v I’ll watch with my eyes closed
x I hope it’s easy to understand
HOGWARTS MYSTERY (Harry Potter) Guide
Pages
Sunday, 23 December 2018
Friendships : Barnaby Lee
Character Info
Meal with Barnaby
Beat Barnaby’s Creature Quiz!
Q: Who specialises in dragons?
A: A Dragonologist
Q: Which creature is from Africa?
A: Fwooper / Phoenix
Q: Which creature can speak?
A: Acromantula / Jarvey
Q: Which creature can fly?
A: Snallygaster / Hippogriff
Q: Name a top creature expert…
A: Gulliver Pokeby / Newt Scamander
Q: Which one makes the best pet?
A: Puffskein
Q: Which creature lays eggs?
A: Chimaera / Augurey
Play Gobstones with Barnaby
Win at Gobstones by confusing Barnaby!
Drink Butterbeer with Barnaby
Prove how well you know Barnaby!
14 comments:
To know more about Chief Dr Lucky you can visit his website (https://chiefdrluckyherbaltherapy.wordpress.com/)
A friend that suffered from Herpes and was cure with the help of this great herbal doctor Chief Lucky so i decided to contact him for help in getting rid of my families genital herpes virus 1/2 which i did and all i was told to provide was just some useful information and some materials used in preparation of the natural cure and that i did and now i am the happiest person on earth because i am writing this testimony of mine with joy and happiness in my heart to the whole world to know that natural remedy is real because i am a living testimony of Chief Lucky traditional herbal cure and i want you all to contact Chief Lucky via his email: chiefdrlucky@gmail.com or WhatsApp him +2348132777335 am sure he will help you too.
i am so glad to write this article today to tell the world how Dr. Ohunyom cured my HPV virus that have been in my body since five years ago, ever since then my life has been in complete,i have used so many drugs that was prescribed to me by several doctors,but it didn’t cure my HPV VIRUS neither did it reduce the pain, i was checking for solution on the internet then miraculously came across Dr. Ohunyom the powerful herbalist that cure HPV INFECTION,then i contacted his email, i explained everything to him and he prepared a herbal cure and send it to me that was how i got cured from HPV disease totally after receiving his herbal medicine, so my friends viewers why waiting and be suffering with this HPV virus when there is someone like Dr. Ohunyom that can get you cured completely. you can contact his Email via:drohunyom@gmail.com and also WhatsApp him +2349060579973 And He also have herbs medicine to cured the following diseases; eczema,urethra wart,chronic problems.Herpes, Cancer, Als,Hepatitis, Diabetes, HPV,Infections,ulcer ETC
Special thanks to Dr.omobhude for helping me get cured from Lupus disease and fibromyalgia, I was tested Positive last 5 months, I contacted him base on the testimonies I’m seeing about him on the Internet, I was cured too by him, this herbal Doctor is capable to heal anything,
1. Fibroid
2. Asthma
3. Diabetes 1/2
4. Cancer stage 1/3
5. Hepatitis B
6. Herpes
7. HPV
kindly contact him today through you can also add Dr.omobhude on WhatsApp +2349050360605 (dr.omobhude1@gmail.com) he can help you
Before people said there is no cure for herpes virus but today many people have now believe that there is a cure,herpes virus can be cured through Africans roots and herbs, Dr.chala he is the one of the great herbal doctor in Africa and he has the cure on this virus last month he share his herbal medicine in some medical hospital and now he is well recognize as one of the best in Africa, you don’t have to be sad any more or share your tears any more on this virus when the cure have already be find by Dr.Chala email him on dr.chalaherbalhome@gmail.com or https://
drchalaherbalhome.godaddysites.com or https://mywa.link/dr.chalaherbalhome
I still cant believe that my herpes is gone after two years of suffering. Thanks to Dr Momoh who cured my herpes with his herbal medication I never thought I will ever be heal again, I was a herpes positive two years ago and I have try so many medication so I can be free of this dearly disease but nothing work out, so one day I go on a research on the internet where I saw someone given testimony on how Dr Momoh help him to cure his herpes virus with his herbal medication, so I said to myself it also the same problem am having so I have to also contact the herbal doctor Dr Momoh on his email which the man recommended to anyone who might also need his help, Wholeheartedly am so grateful to this man as he help me with the cure and make me a happy man again. Anyone out there who might be facing same problem should kindly contact Dr Momoh as is know he will help you with all your problems, contact him through his email dr.momoh9@gmail.com, call or WhatsApp him +2347083724098
Hello, everyone! I,m here to explore blogs and forum about wonderful and most safe cure for (Herpes Virus).I was positive to the deadly virus called herpes and i lost hope because i was out casted and rejected even by my closet friends.i searched on-line to know and enquirer about cure for Herpes and i read someone testimony on how he was cured from Herpes so i decided to contact the same herbalist because i know that nature has the power to heal everything.i contacted him to know how he can help me and he told me never to worry that he will heal me with the natural herbs from God!after 2 days of contacting him, he told me that the cure has been ready and he sent it to me via DHL and it got to me after 3 days!i used the med as he instructed me (MORNING and EVENING) and i was cured!its really like a dream but i am so happy!thats the reason i decided to also add more comment of Him so that more can be saved just like me!and if you need his help, you can email him on drehimare3@gmail.com, or whatsapp +1 (267) 691-1087 I,m neme amber and you can get in touch with me via drehimare3@gmail.com..Contact him for help at Herpes virus HIV/AIDS CANCER COPD BRAIN TUMOR All kind of virus and disease Dr Ehimare
Goodluck in life
and all kind of diseaseHpatities A, B
i am so glad to write this article today to tell the world how Dr. Ohunyom cured my HPV virus that have been in my body since five years ago, ever since then my life has been in complete,i have used so many drugs that was prescribed to me by several doctors,but it didn’t cure my HPV VIRUS neither did it reduce the pain, i was checking for solution on the internet then miraculously came across Dr. Ohunyom the powerful herbalist that cure HPV INFECTION,then i contacted his email, i explained everything to him and he prepared a herbal cure and send it to me that was how i got cured from HPV disease totally after receiving his herbal medicine, so my friends viewers why waiting and be suffering with this HPV virus when there is someone like Dr. Ohunyom that can get you cured completely. you can contact his Email via:drohunyom@gmail.com and also WhatsApp him +2349060579973 And He also have herbs medicine to cured the following diseases; eczema,urethra wart,chronic problems.Herpes, Cancer, Als,Hepatitis, Diabetes, HPV,Infections,ulcer ETC
I had body itching, pain during urination and blistering sores on my genital area. So, I went to the hospital for treatment and was diagnosed for HERPES SIMPLEX VIRUS. I was given some Antiviral medications to reduce the severity, but it got worse with the pain and its reappearing was longer than the disappearing. So, I went seeking other means to cure the disease and that was how I got to know Dr. Oda who helped cure the disease. It’s been a year since I got cured and i haven’t had any pain or symptoms of HSV. Also, i was confirmed negative at the hospital. You too can be rescued by this doctor. Contact: (drodasolution@gmail.com Tel/whatsapp: +234 805 761 6299)
Hi, there. I am Tom Neil and I want to describe how life had been for my younger brother living with schizophrenia and how he had been permanently able to survive this debilitating disorder via a naturopathic, herbal method.
Although he had much academic success as a teenager, his behavior had become increasingly odd during the past year. He quit seeing his friends and no longer seemed to care about his appearance or social pursuits. He began wearing the same clothes each day and seldom bathed. He lived with several family members but rarely spoke to any of them. When he did talk to them, he said he had found clues that his college was just a front for an organized crime operation. He had been suspended from college because of missing many classes. My sister said that she had often seen him mumbling quietly to himself and at times he seemed to be talking to people who were not there. He would emerge from my room and ask my family to be quiet even when they were not making any noise.
My father and sister told the staff that Maicon’s great-grandmother had had a serious illness and had lived for 30 years in a state hospital, which they believed was a mental hospital. Our mother left the family when Maicon was very young. She has been out of touch with us, and they thought she might have been treated for mental health problems.
Maicon agreed to sign himself into the psychiatric unit for treatment. The whole family except I had agreed to have Maicon transferred to a mental asylum. I knew inwardly there was still some plausible means by which my kid brother could overcome this condition. I knew botanical means of treatment will be more favorable than any other type of treatment, and as such, I had taken a keen interest in the research of naturopathic alternative measures suitable for the treatment of schizophrenia. I had pleaded for some little patience from the family in the delay of the transfer, I was looking forward to proving a point to the entire family, of a positive botanical remedy for this condition.
It was during my ceaseless search on the internet I had been fortunate enough to come across Dr. Utu Herbal Cure: an African herbalist and witch doctor whose professional works had majored on the eradication of certain viral conditions, especially schizophrenia, ( improving the memory capacity positively), via a traditional, naturopathic process and distinguished diet plan. It was by the administration of this herbal specialist that my brother had been able to improve his condition for better.
My brother Maicon is just like many other patients out there suffering from this disease. Although he was able to overcome this condition via a naturopathic herbal remedy administered by this African herbal physician and saved completely thus, rekindling the lost joy which had been experienced by the family members.
I wish to use this opportunity to reach across to anyone who may happen to be diagnosed with this disastrous condition to spread the hope of an everlasting herbal remedy that is capable of imposing a permanent end to this disease.
Quick Answer: What’S My Favourite Thing Barnaby?
What is your favorite thing Barnaby
What’s my favourite thing.
How many do we each start with Barnaby
SevenQ. How many do we each start with? – Seven.
How many Gobstones do you start with
fifteenPlayers start the game with fifteen small, round Gobstones each (Gobstones are sold in sets of thirty) and the winner must capture all of his opponent’s stones.
What is the heaviest animal that can fly
great bustardThe great bustard is probably the heaviest living animal that can fly. The males normally weigh between 10 and 16 kilograms, but some can reach 21 kg. For comparison, the wandering albatross has a larger wingspan, but only the biggest reach even 16 kg.
How do you win a Barnaby duel
Most of the times, Barnaby will go with Sneaky stance, so your best bet is to stick with the Aggressive and hit him with Depulso or Incendio. It will take around three casts to beat him, but keep in mind that he will on some occasions go with Defensive.
Which one makes the best pet Barnaby
Q. Which one makes the best pet? – Puffskein.
Where did you meet Barnaby Harry Potter
the Hog’s Head InnWhen Jacob’s sibling learned they were a Legilimens, Barnaby met with them at the Hog’s Head Inn to allow them the opportunity to practice Legilimency on him.
Which creature can fly
The only animals that can truly fly are birds, insects, and bats. Other animals manage to travel through the air by gliding from great heights or leaping from the depths.
Who Spied on your Animagus talk
Q. Who spied on our Animagus talk? – Penny.
What was inside the vault tonks
Q. What was inside the Vault? – Mysterious runes. – A mysterious book.
What creature is from Africa Hogwarts
Magical creatures and plants The Fwooper is native to Africa. The Nundu is native to East Africa. The Phoenix is native to Egypt.
Which makes the best pet Harry Potter
Top Five Coolest Pets in “Harry Potter”Fawkes. Source. Fawkes is basically flawless. … Nagini. Source. Nagini is terrifying but still really cool. … Fluffy. Source. Our favorite three-headed dog has to be included in this list. … Crookshanks. Source. Crookshanks is the best half-Kneazle around and our favorite four-legged detective. … Hedwig.
Who specializes in Harry Potter
A dragonologist is a magizoologist who specialises in the study of dragons.
Does Merula have a crush on MC
People: “There’s no way Merula has a crush on MC.” Me: “oh really?” – HPHogwartsMystery. Find this Pin and more on Harry Potter Still Lives Bois!
Does ismelda like Barnaby
In their fifth year, MC found out Ismelda had a crush on Barnaby after Emily Tyler read Ismelda’s diary out loud in front of everyone. Ismelda asked for MC’s help to deal with her feelings with Barnaby, and MC helped her confess. In the end, this did not work out.
What can fly without wings
The answer to the “what flies without wings” riddle is “time”.
What is a flying animal
A flying animal is any animal that has evolved to fly. There are also gliding animals (volant animals) but they have evolved slightly different to flying animals and they can’t fly on their own. Flying animals have evolved a number of different times without a single ancestor that brings them together.
What happens if you lose Gobstones
A game of Gobstones, “Snake Pit” Rules. Gobstones is a game mostly popular amongst wizarding children played with special stones, similar to the Muggle game of marbles except that when a player loses a point, the gobstone then spits a putrid liquid at the player.
What animals do Porlocks guard
The Porlock guarded horses, and lived on grass. It can either be found nesting in the straw of a stable, or in the middle of the herd it was protecting.
Hogwarts Mystery School
Your source for the Harry Potter: Hogwarts Mystery Video Game
Barnaby Lee Friendship Guide
Who is Barnaby Lee?
Barnaby Lee is a Slytherin in the same year as the Player Character.В He is initially antagonistic towards you as he is friends with Merula Snyde and Ismelda Murk.В You will be able to become friends towards the end of Year 3 as you complete his quests.В Barnaby is considered one of the strongest duelists in the year, however his intelligence is lacking.
Upon becoming friends you will be able to share a meal in the Great Hall, drink butterbeer at the Three Broomsticks in Hogsmeade, and play Gobstones in the Courtyard.В Each activity is a series of four questions which will reward up to three diamonds that translate into experience for Barnaby’s friendship level.В The experience required and reward for each level are as follows:
2 – 80 experience, 5 gem reward.
3 – 100 experience, 5 gem reward
4 – 120 experience, 5 energy reward
5 – 240 experience, 5 energy reward
6 – 360 experience, 10 energy reward
7 – 600 experience, 10 energy reward
8 – 800 experience, 15 energy reward
9 – 1200 experience, 15 energy reward
10 – 1300 experience, Special cosmetic clothing reward: Gray Sweater with your House Crest.
Finally we will go over the answers to every question Barnaby can potentially ask during the activities you complete with him.В Answers in green are worth 10 points while answers in yellow are worth 5.В Some questions will have two 10 point answers.
Meal with a friend
Barnaby likes Magical Creatures and will quiz your character on their knowledge of the field.
Who specializes in dragons?
Dragonologist
Which creature is from Africa?
Fwooper
or
Phoenix
Which creature can speak?
Acromantula
or
Jarvey
Which creature can fly?
Hippogriff
or
Snallygaster
Which creature can lay eggs?
Augurey
or
Chimaera
Which one makes the best pet?
Puffskein
Name a top creature expert
Newt Scamander
or
Gulliver Pokeby
Play Gobstones
Barnaby claims he is good at games as long as he doesn’t get too confused.В Pick the most confusing answers to get maximum points.
Let’s join the Gobstones Club.
We founded the Gobstones Club.
or
Let’s drink confusing Concoction.
What if I lose?
You’ll turn into a Doxy.
or
You’ll get expelled.
Don’t try to confuse me
How does this liquid smell?
or
We’re supposed to be standing.
Let’s play, (your player character’s name)
Why do they call it Gobstones?
or
How do we know who goes first?
How do you like Gobstones?
Gobstones are my favourite food.
or
It’s confusing.
Wait until you see this move…
I just saw it
or
I’ll watch with my eyes closed.
You might beat me…
Just think about Arithmancy.В
or
Just think about exams.
Drink Butterbeer
Who was I friends with before?
Merula
or
Ismelda
Where did we meet?
Potions Class.
Who’s my Head of House?
Professor Snape
Who did my dad used to know?
You-know-who
or
Horace Slugorn
What am I best known for?
Being tough.
What’s my favorite thing?
Creatures
or
Dueling
What’s my surname?
Lee
Permutations and Combinations
A combination of a given number of articles is a set or group of articles selected from those given where the order of the articles in the set or group is not taken into account.
A permutation of a given number of articles is a set or group of articles selected from those given where the order of the articles in the set or group is taken into account.
At that point we looked at straightforward questions and often used the formulae to calculate the number of permutations or combinations. We will now look at some more complicated examples where the formulae do not work directly.
Permutations
Example 1
How many arrangements can be made of three letters chosen from the word PLANTER if the first letter is a vowel and each arrangement contains three different letters?
Solution
We split this into two separate calculations.
Assume we begin with the letter A. Hence the other two letters can be chosen in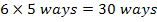 
.
If we begin with the letter E, then the other two letters can also be chosen in 30 ways.
Since these are the only two possibilities for beginning with a vowel, there are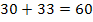 
possible permutations.
Example 2
How many three-digit numbers can be made from the set of integers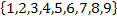 
if
a) the three digits are all different
b) the three digits are all the same
c) the number is greater than 600
d) the number is even and each digit can only be used once?
Solution
a) The first digit can be chosen in nine ways.
The second digit can be chosen in eight ways.
The third digit can be chosen in seven ways.
Total number of three-digit numbers that are all different 
b) If the three digits are all the same then there are nine possible three-digit numbers, since the only possibilities are 111, 222, 333, 444, 555, 666, 777, 888 and 999.
c) If the number is greater than 600 then there are only four choices for the first digit: 6, 7, 8 or 9.
The second and third digits can each be chosen in nine ways.
Total number of three-digit numbers 
d) In this case we start with the last digit as this is the one with the restriction.
The last digit can be chosen in four ways.
The other two digits can be chosen in eight ways and seven ways respectively.
Total number of three-digit numbers that are all different 
Example 3
In how many ways can six people be sat around a circular dining table?
Solution
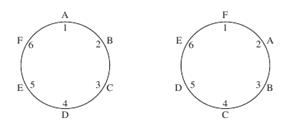
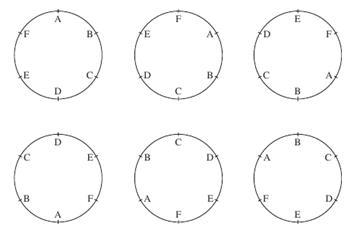
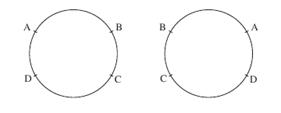
At first this appears to be a simple permutation, where the answer is 6! However, if we look at the two situations below, where the chairs are labelled from 1 to 6 and the people from A to F, we can see that they appear as different permutations, but are actually the same.
Because of the actual situation, every person has the same people on either side in both cases. If the chairs had been distinguishable, then this would no longer be the case. 
Hence for every permutation of people sat around the table, there are five more permutations which are the same and hence the answer is six times too big. These are shown in the diagram below. 
Therefore the number of ways that six people can be sat around a circular dining table is 
NOTE!For any situation like this the answer can be generalised to 
Example 4
Jenny is making a necklace. In how many ways can 4 beads chosen from 12 beads be threaded on a string?
Solution
This is similar to the example above. As with the example above the answer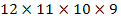 
needs to be divided by 4 because of the repetitions caused by the fact that it is on a circle. However in this situation there is another constraint because the necklace can be turned over giving an equivalent answer. In the diagrams below, these two situations are actually the same, but appear as two separate permutations of the answer.
Hence we need to divide the answer by 2.
Therefore the number of permutations is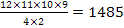 
.
Example 5
a) Find the number of arrangements of the letters of the word LITTER.
b) Find the number of arrangements where the T’s are together.
c) Find the number of arrangements where the T’s are separated.
Solution
a) In this question we treat it as a simple permutation and hence the answer would appear to be 6! However, the two T’s are indistinguishable and hence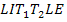 
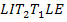
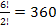
and 
are actually the same arrangement but appear as two separate permutations. As this happens in every single case the number of arrangements is 
.
b) With the T’s together we treat the two T’s as one letter. If we give TT the symbol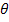 
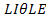
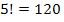
, then we are finding the permutations of 
, which are 
arrangements.
c) For the T’s separated, we remove the T’s initially and find the number of permutations of LIER which is 4!
If we now consider the specific permutation REIL, then the two T’s can be placed in two of five positions. This is shown in the diagram below.
Hence for the permutation REIL there are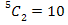 
ways of positioning the T’s. As this can happen with each of the 4! permutations of the four letters, then the total number of permutations is 
arrangements.
We could also think about this another way. As we know the total number of arrangements is 360 and the T’s either have to be together or separated then the number of arrangements where they are separated is 360 minus the number of arrangements where they are together.
This gives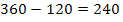 
arrangements.
Example 6
Find the number of arrangements of the letters in the word REFERENCE where the E’s are separated.
Solution
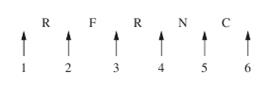
We begin by considering RFRNC. The number of arrangements of these letters is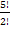 
since the two R’s are indistinguishable.
Again considering one possible arrangement of the letters, say RFNRC, the positions that the three E’s can take are shown below.
We need to find the number of combinations of four from six positions, which is 
Hence the number of arrangements where the E’s are separated is 
Combinations
Example 1
A team of 4 children is to be selected from a class of 20 children, to compete in a quiz game. In how many ways can the team be chosen if
a) any four can be chosen
b) the four chosen must include the oldest in the class?
Solution
a) This is a straightforward combination with an answer of 
b) In this situation we remove the oldest in the class since this child has to be part of every group. Hence the problem is actually to find how many teams of 3 children can be found from 19. Therefore the number of teams is 
Example 2
Ten students in a class are divided into two groups of five to play in a five-a-side soccer tournament. In how many ways can the two teams of five be selected?
Solution
This appears to be very similar to the example above, but there is a subtle difference. The number of ways of selecting a team of five is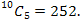 
Let us imagine that the chosen team is ABCDE. Hence the other team would automatically be FGHIJ. However another possible combination of a team of
five would be FGHIJ and this would then automatically select the other team as ABCDE. In other words the calculation picks each pair of teams twice. Hence the actual number of teams is 
Example 3
Anisa goes into her local supermarket and finds that there are 20 different types of chocolate on offer and 15 different types of soft drink. She wants to buy seven different bars of chocolate and four different cans of soft drink for herself and her friends. Find the number of different ways in which she can do this.
Solution
The number of ways she can choose seven bars of chocolate is 
The number of ways she can choose four cans of soft drink is 
Since with any particular combination of chocolate bars she can put all the particular combinations of cans of soft drink, the total number of choices is 77 520 
1365 = 105 814 800.
Example 4
A box contains four red, two blue, one yellow and one pink ball. How many different selections of three balls may be made?
Solution
All three the same: The only possibility here is three red balls and hence there is only one way of doing this.
Two the same, one different: There are two possibilities for two the same, red and blue. The third ball can then be chosen from any of the others, so there are three possibilities because we cannot choose the same colour again. Therefore the total number of ways is 
All three different: Since there are four different colours of ball this is 
Hence the number of different selections that can be made is 
NOTE!Unlike the previous example, we added the combinations here as opposed to multiplying them.
EXERCISES
Exercises (using permutations and combinations)
1. In how many ways can six different files be arranged in a row on a desk?
2. In how many ways can two boys and two girls be chosen from a group of 15 boys and 18 girls?
3. In how many ways can four different letters be put in four different envelopes?
4. In how many ways can three different coats be arranged on five hooks in a row?
5. Giulia has ten different mathematics books and four different chemistry books. In how many ways can she arrange seven of the mathematics books and one chemistry book on a shelf if the chemistry book must always be at one end?
6. In how many ways can the letters of the word PHOTOGRAPH be arranged?
7. Two sets of books contain seven different novels and four different autobiographies. In how many ways can the books be arranged on a shelf if the novels and the autobiographies are not mixed up?
8. In how many ways can ten different examinations be arranged so that the two mathematics examinations are not consecutive and the two French examinations are not consecutive?
9. Given that each digit can be used more than once, how many two-digit numbers can be made from the set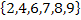 
if
a) any two digits can be used
b) the two digits must be the same
c) the number must be odd
d )the number must be greater than 60?
10. A quiz team of five students is to be chosen from nine students. The two oldest students cannot both be chosen. In how many ways can the quiz team be chosen?
11. Consider the letters of the word DIFFICULT.
a) How many different arrangements of the letters can be found?
b) How many of these arrangements have the two I’s together and the two F’s together?
c) How many of the arrangements begin and end with the letter F?
12. Margaret wants to put eight new plants in her garden. They are all different.
a) She first of all decides to plant them in a row. In how many ways can she do this?
b) She then decides that they would look better in a circle. In how many ways can she do this?
c) She now realizes that two of the plants are identical. How many arrangements are there for planting them in a row and for planting them in a circle?
13. a) How many different arrangements of the word ARRANGEMENT can be made?
b) How many arrangements are there which start with a consonant and end with a vowel?
14. Jim is having a dinner party for four couples.
a) In how many ways can the eight people be seated at Jim’s circular dining table?
b) John and Robin are a couple, but do not want to sit next to each other at the dinner party. In how many ways can the eight people now be seated?
c) Jim decides that the two oldest guests should sit next to each other. In how many ways can the eight people now be seated?
15. a) How many numbers greater than 300 can be made from the set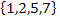 
if each integer can be used only once?
b) How many of these numbers are even?
16. a) A local telephone number has seven digits and cannot start with zero. How many local numbers are there?
b) The telephone company realizes that they do not have enough numbers. It decides to add an eighth digit to each number, but insists that all the eight-digit numbers start with an odd number and end with an even number. The number still cannot start with a zero. Does this increase or decrease the number of possible telephone numbers and if so by how many?
17. a) How many different arrangements are there of the letters of the word INQUISITION?
b) How many arrangements are there where the four I’s are separate?
c) How many arrangements are there where the S and the T are together?
18. Five different letters are written and five different envelopes are addressed. In how many ways can at least one letter be placed in the wrong envelope?
19. On an examination paper of 20 questions a student obtained either 6 or 7 marks for each question. If his total mark is 126, in how many different ways could he have obtained this total?
20. Four boxes each contain six identical coloured counters. In the first box the counters are red, in the second box the counters are orange, in the third box the counters are green and in the fourth box the counters are purple. In how many ways can four counters be arranged in a row if
a) they are all the same
b) three are the same and one is different
c) they are all different
d) there is no restriction on the colours of the counters?
21. a) In how many ways can six different coloured beads be arranged on a ring?
b) If two beads are the same colour, how many ways are there now?
22. a) How many different combinations of six numbers can be chosen from the digits 1, 2, 3, 4, 5, 6, 7, 8 if each digit is only chosen once?
b) In how many ways can the digits be divided into a group of six digits and a group of two digits?
c) In how many ways can the digits be divided into two groups of four digits?
23. A shop stocks ten different types of shampoo. In how many ways can a shopper buy three types of shampoo if
a) each bottle is a different type
b) two bottles are the same type and the third is different?
24. A mixed team of 10 players is chosen from a class of 25 students. 15 students are boys and 10 students are girls. In how many ways can this be done if the team has five boys and five girls?
25. Find the number of ways in which ten people playing five-a-side football can be divided into two teams of five if Alex and Bjorn must be in different teams.
26. A tennis team of four is chosen from seven married couples to represent a club at a match. If the team must consist of two men and two women and a husband and wife cannot both be in the team, in how many ways can the team be formed?
27. Nick goes to the shop to buy seven different packets of snacks and four bottles of drink. At the shop he find he has to choose from 15 different packets of snacks and 12 different bottles of drink. In how many different ways can he make his selection?
28. In how many ways can three letters from the word BOOKS be arranged in a row if at least one of the letters is O?