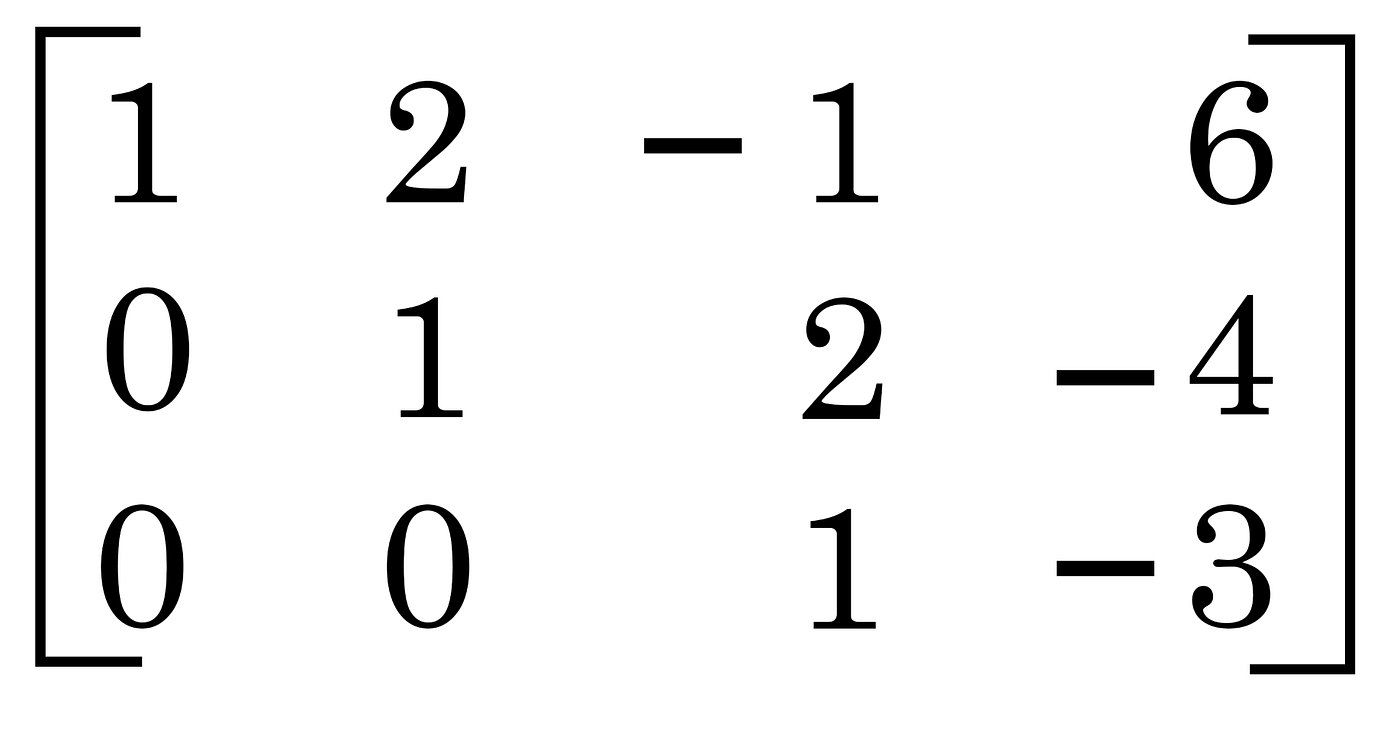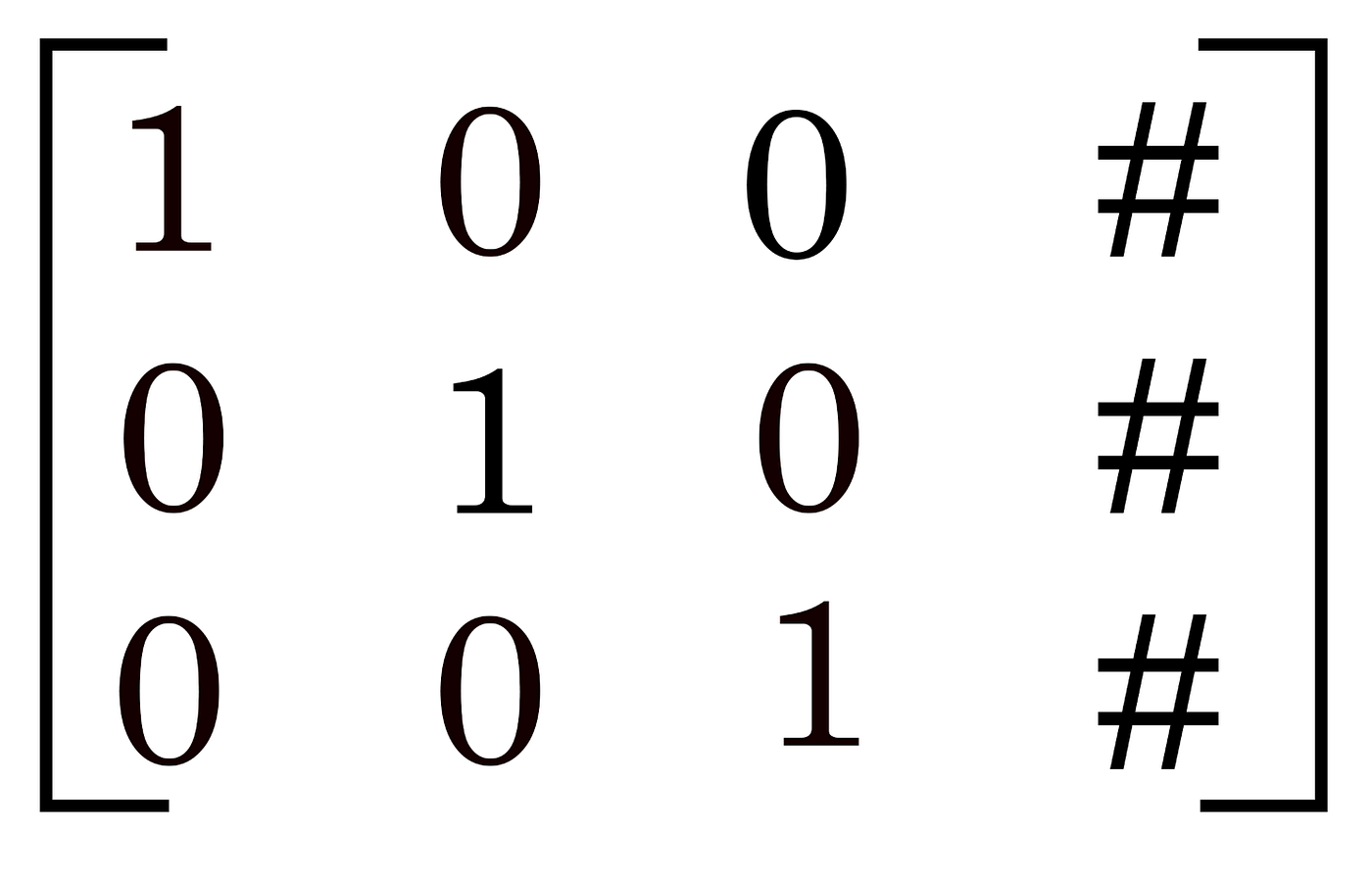How to solve to equations
How to solve to equations
Solving Equations
What is an Equation?
An equation says that two things are equal. It will have an equals sign «=» like this:
That equations says: what is on the left (x − 2) is equal to what is on the right (4)
So an equation is like a statement «this equals that«
What is a Solution?
A Solution is a value we can put in place of a variable (such as x ) that makes the equation true.
Example: x − 2 = 4
When we put 6 in place of x we get:
So x = 6 is a solution.
In this case x = 6 is the only solution.
More Than One Solution
There can be more than one solution.
Example: (x−3)(x−2) = 0
When x is 3 we get:
And when x is 2 we get:
which is also true
So the solutions are:
When we gather all solutions together it is called a Solution Set
The above solution set is:
Solutions Everywhere!
Some equations are true for all allowed values and are then called Identities
Example: sin(в€’θ) = в€’sin(θ) is one of the Trigonometric Identities
So it is true for θ = 30°
So it is also true for θ = 90°
Is it true for all values of θ? Try some values for yourself!
How to Solve an Equation
There is no «one perfect way» to solve all equations.
A Useful Goal
But we often get success when our goal is to end up with:
In other words, we want to move everything except «x» (or whatever name the variable has) over to the right hand side.
Example: Solve 3x−6 = 9
Now we have x = something,
and a short calculation reveals that x = 5
Like a Puzzle
In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.
Here are some things we can do:
Example: Solve √(x/2) = 3
And the more «tricks» and techniques you learn the better you will get.
Special Equations
Check Your Solutions
You should always check that your «solution» really is a solution.
How To Check
Take the solution(s) and put them in the original equation to see if they really work.
Example: solve for x:
2xx − 3 + 3 = 6x − 3 (x≠3)
We have said x≠3 to avoid a division by zero.
Let’s multiply through by (x − 3) :
Bring the 6 to the left:
Expand and solve:
2x + 3x − 9 − 6 = 0
That can be solved by having x=3
2 × 3 3 − 3 + 3 = 6 3 − 3
Hang On!
That means Dividing by Zero!
x = 3 does not actually work, and so:
There is No Solution!
This gives us a moral lesson:
«Solving» only gives us possible solutions, they need to be checked!
How to Solve Two Step Algebraic Equations
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 110 people, some anonymous, worked to edit and improve it over time.
There are 10 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 665,444 times.
\u00a9 2022 wikiHow, Inc. All rights reserved. wikiHow, Inc. is the copyright holder of this image under U.S. and international copyright laws. This image is not licensed under the Creative Commons license applied to text content and some other images posted to the wikiHow website. This image may not be used by other entities without the express written consent of wikiHow, Inc.
\n
\u00a9 2022 wikiHow, Inc. All rights reserved. wikiHow, Inc. is the copyright holder of this image under U.S. and international copyright laws. This image is not licensed under the Creative Commons license applied to text content and some other images posted to the wikiHow website. This image may not be used by other entities without the express written consent of wikiHow, Inc.
\n
\u00a9 2022 wikiHow, Inc. All rights reserved. wikiHow, Inc. is the copyright holder of this image under U.S. and international copyright laws. This image is not licensed under the Creative Commons license applied to text content and some other images posted to the wikiHow website. This image may not be used by other entities without the express written consent of wikiHow, Inc.
\n
\u00a9 2022 wikiHow, Inc. All rights reserved. wikiHow, Inc. is the copyright holder of this image under U.S. and international copyright laws. This image is not licensed under the Creative Commons license applied to text content and some other images posted to the wikiHow website. This image may not be used by other entities without the express written consent of wikiHow, Inc.
\n
Fundamentals in solving equations in one or more steps
Formulas are very common within physics and chemistry, for example, velocity equals distance divided by time. Thus we use the common symbols for velocity (v), distance (d) and time (t) and express it thus:
We may simply describe a formula as being a variable and an expression separated by an equal sign between them. In other words a formula is the same as an equation.
Example
| Number of books | Cost |
| 1 | 10 + 2 ∙ 1 = 12 |
| 2 | 10 + 2 ∙ 2 = 14 |
| 3 | 10 + 2 ∙ 3 = 16 |
| 4 | 10 + 2 ∙ 4 = 18 |
| 5 | 10 + 2 ∙ 5 = 20 |
| x | 10 + 2x |
If we designate the total book club cost as C, we may derive the following formula for the expression:
When we want to solve an equation including one unknown variable, as x in the example above, we always aim at isolating the unknown variable. You can say that we put everything else on the other side of the equal sign. It is always a good idea to first isolate the terms including the variable from the constants to begin with as we did above by subtracting or adding before dividing or multiplying away the coefficient in front of the variable. As long as you do the same thing on both sides of the equal sign you can do whatever you want and in which order you want.
Above we began by subtracting the constant on both sides. We could have begun by dividing by 2 instead. It would have looked like
Again the same answer just proving the point.
If your equation contains like terms it is preferable to begin by combining the like terms before continuing solving the equation.
Example
Begin by combining the like terms (all terms including the same variable x and all constants)
$$\left (5x +2x \right )+\left (14+2 \right )=30$$
Now it’s time to isolate the variable from the constant part. This is done by subtracting 16 from both sides
Divide both sides by 7 to isolate the variable
If you have an equation where you have variables on both sides you do basically the same thing as before. You collect all like terms. Before you have worked by first collecting all constant terms on one side and keep the variable terms on the other side. The same applies here. You collect all constant terms on one side and the variable terms on the other side. It’s usually a good idea to collect all variables on the side that has the variable with the highest coefficient i.e. in the example below there are more x:es on the left side (4x) compared to the right side (2x) and hence we collect all x:es on the left side.
Example
subtract 2x from both sides
Now it looks like any other equation
subtract 3 from both sides
Divide by 2 on both sides
In the beginning of this section we showed the formula for calculating the velocity where velocity (v) equals the distance (d) divided by time (t) or
If we by some chance want to know how far a truck drives in 3 hours at 60 miles per hour we can use the formula above and rewrite it to solve the distance, d.
When that’s done we can just put our numbers in the formula and calculate the answer
The truck travels 180 miles in 3 hours.
This holds true for all formulas and equations.
Video lesson
Solve the equation
$$3\left (x + 2 \right )- 3 + x + 17 = 40$$
Ratios and proportions and how to solve them
Let’s talk about ratios and proportions. When we talk about the speed of a car or an airplane we measure it in miles per hour. This is called a rate and is a type of ratio. A ratio is a way to compare two quantities by using division as in miles per hour where we compare miles and hours.
A ratio can be written in three different ways and all are read as «the ratio of x to y»
A proportion on the other hand is an equation that says that two ratios are equivalent. For instance if one package of cookie mix results in 20 cookies than that would be the same as to say that two packages will result in 40 cookies.
A proportion is read as «x is to y as z is to w»
If one number in a proportion is unknown you can find that number by solving the proportion.
Example
You know that to make 20 pancakes you have to use 2 eggs. How many eggs are needed to make 100 pancakes?
| Eggs | pancakes | |
| Small amount | 2 | 20 |
| Large amount | x | 100 |
If we write the unknown number in the nominator then we can solve this as any other equation
Multiply both sides with 100
If the unknown number is in the denominator we can use another method that involves the cross product. The cross product is the product of the numerator of one of the ratios and the denominator of the second ratio. The cross products of a proportion is always equal
If we again use the example with the cookie mix used above
It is said that in a proportion if
If you look at a map it always tells you in one of the corners that 1 inch of the map correspond to a much bigger distance in reality. This is called a scaling. We often use scaling in order to depict various objects. Scaling involves recreating a model of the object and sharing its proportions, but where the size differs. One may scale up (enlarge) or scale down (reduce). For example, the scale of 1:4 represents a fourth. Thus any measurement we see in the model would be 1/4 of the real measurement. If we wish to calculate the inverse, where we have a 20ft high wall and wish to reproduce it in the scale of 1:4, we simply calculate:
$$20\cdot 1:4=20\cdot \frac<1><4>=5$$
Video lesson
How to Solve 3 Variable Systems of Equations: Beginner’s Guide
So you’ve graduated from two-variable systems of equations to the big leagues, three-variable, three equation systems! Gone are the days of simple Substitution and Elimination methods and welcome to the world of nearly page-long solutions.
In this guide, you’ll learn about two different techniques you can use to solve these complicated systems. Let’s jump in!
What is a Three-Variable System of Equations?
The first question you may have is what exactly is this three-variable system? You may remember from two-variable systems of equations, the equations each represent a line on an XY-coordinate plane, and the solution is the (x,y) intersection point for the two lines. In other words, the solution is the value or values for x and y that hold true for both equations.
Three variable systems of equations aren’t so different. The solution still represents the values for x, y, and z (or whatever variables your equations are using) that when plugged into each equation holds true.
Visually, a three-variable equation is represented in 3-dimensional space as a plane in the xyz-coordinate axis. Don’t worry, you seldom will be asked to graph a set of three variable systems in 3D space. It’s probably sufficient for you to understand that the solution to your three-variable system of equations is the values that will make all three equations true and represents the intersection of three planes in 3D space.
Three Variables, Three Equations
In general, you’ll be given three equations to solve a three-variable system of equations. This is similar to how you need two equations to solve a standard system of linear equations. In some cases, you may be able to solve a three-variable system of equations with only two equations, but it isn’t as common.
Two Methods
If you are in second-year Algebra or PreCalculus, most likely you’ll be using the Backsolving Method. If you are in a Linear Algebra or computer programming course, you’ll probably be asked to solve using Gaussian Elimination with matrices.
The Backsolving Method
The Backsolving Method is reminiscent of the Elimination Method from our standard systems of equations arsenal. In fact, you’ll be using the Elimination method multiple times in the course of the backsolving method.
The basic idea behind the backsolving method is to take your 3 three-variable equations and make 2 two-variable equations so that you can solve them using the traditional substitution or elimination methods. Once you find one variable’s solution, you can then back solve to find the solutions for the other two variables.
It’s a bit tedious, but a fairly simple process once you get the hang of it. In the following video tutorial, I demonstrate how to choose two sets of two equations to perform the elimination method on, and then back solve to solve for all three variables.
The key to completing the backsolving method successfully is to eliminate the same variable from your two sets of three-variable equations. This ensures that the two resulting two-variable equations are capable of being solved using the substitution or elimination methods. Again, this is easier in practice so check out the tutorial below to see it in action 🙂
Gaussian Elimination
If you’re familiar with matrices, Gaussian Elimination is a wonderful way to solve three-variable systems of equations as well as systems with more variables and more equations. There is quite a bit of set up work involved in order to use this method, but the payoff is once you have it set up the system is straightforward to solve.
The basic idea is to translate your system of equations into a matrix using placeholder zeroes and ones where needed. Once you have the matrix set up, you can begin manipulating it by using basic properties of matrices. The process is like a game where you add, subtract, multiply, and divide the rows in your matrix in order to make zeroes and ones in specific locations.
As you work through your matrix, you’ll be working to “row-echelon” and/or “reduced row echelon” form. Row echelon is when you have a diagonal of ones going from the upper left to the second-to-the-right bottom row and under all the ones you have zeroes.
Reduced row echelon form is when in addition to having the diagonal of ones and zeroes beneath, you also have zeroes above the ones. Reduced row echelon form is ideal because you can easily read off the solution to your system of equations without any additional work.
To learn how to solve a 3×3 system of equations using Gaussian Elimination, check out the video tutorial below. Once again it’s easier in practice than it sounds in writing!
Infinitely Many & No Solution Explained
Just like with two variable systems of equations you can have infinitely many solutions or no solution. Since we’re now working with three planes instead of two lines, we have more scenarios that can result in infinite or no solution.
Infinitely Many Solutions
There are multiple ways you could wind up with infinite solutions in a three-variable system of equations. The most obvious is that the three planes could be the same so that a solution to one equation will be the solution to all of the equations. Another possibility is that all of the equations are different but they intersect in a line, and we know from our standard system of equations that a linear solution set is infinitely many solutions. Lastly, we could have two equations that are the same plane that intersect the third plane forming a line.
No Solution
There are a few different scenarios that leave you with no solution when dealing with three variable systems. The most common is that you have three parallel planes that never intersect and therefore have no intersection points. Another possibility is you have two parallel planes and one intersecting plane or three planes that intersect but not at the same location.
In all of the scenarios, you are unable to produce a point or set of points that represent the intersection of all three planes. Fortunately, if you are using Gaussian Elimination no solution results are really easy to detect because you will stumble across a row that translates into a false statement, such as 0=1 or some similar contradiction. This is your indicator that the system has no solution, and remember if it has no solution the system is inconsistent.
Dependent, Independent, & Inconsistent Systems
Any system you have will fall into one of three categories: dependent, independent, or inconsistent.
Dependent System
A dependent system has infinitely many solutions. Recall from above that there are multiple ways your system could produce an infinite number of solutions (all three planes are the same plane or they intersect to form a line).
Independent System
If a dependent system has infinitely many solutions, then an independent system has a single solution. For an intersection of three planes, you’ll end up with an (x, y, z) coordinate as your solution, or in other words a value for each variable in your system.
Inconsistent System
A system is inconsistent if there is no solution.
The Opposite of Inconsistent must be Consistent
And finally, if it’s not inconsistent it must be consistent, which means that it has at least one solution. A system is consistent if it has a solution — it can be one solution (i.e a coordinate point answer) or infinitely many solutions, so long as there is a solution!
Источники информации:
- http://www.wikihow.com/Solve-Two-Step-Algebraic-Equations
- http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/fundamentals-in-solving-equations-in-one-or-more-steps
- http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
- http://medium.com/i-math/how-to-solve-3-variable-systems-of-equations-beginners-guide-72c12cf7434c