How to use abacus
How to use abacus
Using ABACUS
ABACUS: Apps Based Activities for Communicating and Understanding Statistics
Mintu Nath
2019-09-12
Main Features
A Quick Start Guide to ABACUS
There are TWO options to explore ABACUS. A brief outline is given here. See the INPUTS and OUTPUTS sections for further details.
Option 1: Replicable simulation given a seed value
If you are using ABACUS for the first time, consider the default input values and just click the Update button. Explore the outcomes in different tabs.
Option 2: Non-replicable instant simulation
INPUTS
Here is a quick guideline on how to use the apps effectively. Different apps may need different types of inputs and display different outputs, but the general framework remains the same.
The options to provide INPUT values are on the left panel of the apps. All inputs are set at appropriate default values, but one can change the input values if needed.
The required INPUT values will depend on the specific app. These may include:
To use the app at first instance, accept the default INPUT values and click the Update button. The app will produce the outcomes in different tabs. Explore the outcomes to understand the apps in the first instance.
To alter the input values, provide the inputs for the Population Parameters (for example, \(\mu\) and \(\sigma\) ) in the text box and alter the other input values by moving the slider bar within the given range. Depending on the Simulation Feature option, the outputs in different tabs will change with altered inputs.
To fine-tune the INPUT values in the slider to the required value, you may select and drag the point nearer the desired value and then press left or right arrow keys to fine-tune.
Simulation Features
There are two options to run repeated random sampling:
Option 1: Replicable simulation given a seed value
When you press the Update button the first time, it will draw a random sample based on the INPUT values. The random sample will be drawn given the seed value included in the text box for seed value (default is given as 12345).
In the next step, you may wish to alter the inputs again OR keep the inputs unaltered and press the Update button again. This will conduct a second random sampling conditional on the given INPUT values.
For example, reload the app for Normal distribution. Keep all the INPUT values at its default values including the seed value as 12345. Click the Update button THREE times. Note the Sample Mean and SD displayed in the plot on the right (see the app). Three successive values displayed should be as follows:
Since we generated the sample from a pre-specified seed value (here 12345, but you can change it to any value), these outcomes are replicable. That means if you reload the app and do it again, you will get the identical three values of \(\bar
Option 2: Non-replicable instant simulation
If you wish to explore many scenarios and do not necessarily wish to replicate your outputs, then select the option: Check the box to update instantly. The important difference here is that you cannot obtain multiple outcomes for the same input values as in Option 1. You have to change the input values (at least a minor change) to trigger the app to sample data again. In other words, the app in this option only вЂreacts’ when you change the INPUT values. Also, note that the Update button will not respond in this option and the random sampling will not be conducted using the seed value (as in Option 1). In Option 2, the seed value is instantly set based on the current time and process id, therefore, outputs are not replicable.
App-specific Inputs
Normal Distribution
Sampling Distribution
Hypothesis Testing: One-Sample Z-Test
Hypothesis Testing: One-Sample Student’s t-Test
Hypothesis Testing: Two-Sample Independent (Unpaired) t-Test
Hypothesis Testing: One-way Analysis of Variance
OUTPUTS
The outcomes are presented in several tabs depending on the app.
How to use an Abacus for Basic Math Operations?
Aug 19, 2021 | Turito Team USA
Everything in the world is based on Math and counting numbers. The greatness of Math is not just for cracking an examination like the SAT, but an important life skill. Abacus is a fun way to learn Math and perform calculations. Abacus has a long history – when it was invented as just a simple machine back in Babylon about 5000 years ago.
This interesting term Abacus is derived from the Greek term ABAX ( Calculating Table). With the help of an Abacus that allows the users to perform arithmetic and basic calculations such as addition, subtraction, multiplication, and division. The abacus consists of sticks arranged horizontally. The beads of each stick can be moved further or down during the calculation.
Because of the visual representation of numbers, the students can easily understand how the calculations happen. Abacus is a fun-filled math tool that every student enjoys, rather than the pen and paper method of doing lengthy and boring math calculations.
Abacus is mainly used for basic arithmetic and algebraic calculations as well. Scientifically, many students who practice Abacus find their critical thinking levels significantly improve. It no longer makes Math a boring subject but indeed- an exciting one.
It is a resourceful subject that not only helps to excel in mathematical calculations but also improves logical reasoning and calculative abilities. With most of the competitive examinations such as SAT and ACT requiring Maths and Reasoning, learning Abacus can be one big advantage to get higher scores. As a result, many educational institutions are making Abacus an important subject for obvious benefits.
With scientifically proven improvement in math skills using Abacus, one can perform basic arithmetic such as addition, subtraction, multiplication, and division with the help of the Abacus in lesser computational time. Along with basic arithmetic, one can also dwell deeper into Algebra and Polynomial equation solving with Abacus. In this blog, we bring you the simple steps that the students can follow to perform basic arithmetic using Abacus:
Performing counting with the help of Abacus:
Each of the beads in the lower should be arranged as a value 1.
Once the five beads are counted, they should be moved to the upper row.
After the upper beats on the upper row are counted and carried forward to the left-adjacent column.
The right column represents the units column and the result is moved to the left-most adjacent column.
How can Abacus be used for Addition?
Ten Strategy:
In this strategy, if you prefer to add 9 and 6, you will have to add 6 and 9 in the first two columns. After moving from 6 to 9- then 9 becomes 10, and 6 becomes 5.
Two 5 Strategy:
To have 5 and 8, add the same number of beads in the first two wires. A total of two 5 becomes 10 and the remaining beads are three. Added 10 plus three gives 13.
How to add bigger numbers?
If you wish to add two double-digit numbers such as 64 and 78. The first wire on the right will have 8 and the second wire will have 7. Add 8+7=16. Keep the digit 6 and pass on 1 to 7.
The final result occurs after adding the remains of these first numbers.
How do you use Abacus for Multiplication?
Then follow the strategy of five, as mentioned above. So now they have to perform 5+5+5+5 = 20 and 1+1+1+1 = 4. Finally, they will have to add 20+4 = 24.
Well, the above-mentioned strategy can only be utilized in the case of small numbers. There may be situations wherein the student confronts large numbers. In those cases, we will follow a different approach.
Step 1 – Assign one letter into each column. So it will become “3”, “4”, “X”, “1”, “2”, and “=”.
This makes us feel the first six wires. Leave the rest of the columns to the right as it is for the answer.
Remember, “X” and “=” will be represented by blank columns.
Step 2 – Multiply 3 with 1 and then 3 with 2. Next, you will multiply 4 with 1 and then 4 with 2.
Understand the pattern. This is the part which we will apply for all kinds of numbers.
Step 3 – Record the results of the products in the correct order. Start recording the first product i.e. 3×1 = 3 in the seventh wire.
Next, 3×2 = 6, record it after the column in which you recorded 3 i.e. eighth wire.
Step 4 – When you multiply 4×1, add the result i.e. 4 to the previous multiplication which we did i.e. 3×2 = 6. Now, 4+6 becomes 10.
Carry one to the seventh wire which was 3 and now it becomes 4 and the eighth wire becomes 0.
Step 5 – Perform the last multiplication which is 4×2 = 8. Recorded in the ninth wire. So our answer is 408.
Conclusion:
Abacus is a very useful tool and a well-proven method to perform arithmetic calculations and improves the memory of the student. The visual representation of each bead makes the student understand the math concepts much easier. Most schools these days are emphasizing the students learning abacus to get better in math and also improve in lateral thinking and critical thinking skills.
Irrespective of the main professional stream the student would plan to take, Abacus can become a crucial life skill that can come a long way down for helping them in calculations, programming skills, and decision-making skills as well. It is relatively simpler to understand and master at a short notice, and hence young students are easily able to pick it up with ease.
Be ahead of the Mathematical game, Master the art of the Abacus!
Understanding How To Use an Abacus
How To Effectively Use The Abacus
An abacus is basically a wooden calculator, but it’s so much more than that. It’s a math developing tool for kids that’s disguised as a toy. The abacus helps with patterns, color recognition, and aids to develop a visual and tactile relationship with numbers. Best of all it’s fun. You get slide & clank beads loudly back and forth while calculating complex algorithms of data. Who wouldn’t want this for their kids and themselves?
If you pair an abacus with the song Smarter 123s, your kids will be a counting, calculating, math wiz in no time.
Fun fact, “abaci” and “abacuses” are both acceptable plural versions of abacus. I don’t know about you, but I find those plural versions extremely fun to just blurt of nowhere. Try it.
History of Abacuses
Credit to who invented the abacus is under debate. The earliest form of an abacus was used over five thousand years ago and was possibly invented in Greece. However, many scholars have compelling arguments for the Phoenicians, Babylonians and even Chinese.
It is interesting to note that it was in use centuries before any modern written numeral system existed. Abacus is a Latin word which was taken from the Greek word abax, which means “board covered with sand.” This was likely a reference to a type of counting board that was the predecessor of the modern abacus and was simply a portable sand table where marks were made in the sand to record totals.
The more familiar form of the modern abacus was definitely used in Ancient Rome from 753 B.C.E. to 476 C.E. but because it was made of wood, only a small number of these have ever been found. Those that were found in Rome resembled the Chinese abacus suggesting that the use of the abacus spread from Greece and Rome to China, and then to Japan and Russia.
Know Your Abacus
In order to use an abacus, we must first understand how it is constructed and how its parts work to perform counting and mathematical operations. The following descriptions are of the Chinese abacus.
1. Frame
The frame is fairly self-explanatory. It is the outside of the abacus and the part that holds the entire apparatus together and in place.
2. Beam
(Also called the Crosspiece) The beam runs parallel to the top and bottom of the frame. It runs across the entire frame and divides the upper deck from the lower deck.
3. Decks
There are two decks: an upper deck and lower deck. The upper deck is used for keeping track of very large groups of sums and the lower deck is used for individual and smaller sums.
4. Rods
Rods run perpendicular to and through the beam. The rods contain beads that are slid towards the beam or away from it. Each rod contains seven beads. Two beads in the upper deck and five beads in the lower deck.
The rod to the farthest right of the abacus represents the ones column. The rod to the left of the “ones” column represents “tens” and to the left of that is the “hundreds” rod. This progresses for as many rods as the abacus contains.
5. Beads
Beads represent numerical values depending on which rod and deck they are housed in.
6. House Points (also called Unit Points or Separation Dots)
There may be small dots on the front of the abacus, called House points. Or, there may be off-colored beads. These are markers used to separate numbers into sets of three, just like we use commas.
These features can also mark a position if you do not want to start counting from the far right. These features can also be useful for including decimals or fractions for counting or calculations.
How To Use Abacus for Kids?
After kids grasp the concept of counting to ten on their fingers, they are ready to learn how to use an abacus for counting and to make basic mathematical computations such as addition and subtraction. After your child understands the simple operations, he is ready to learn the more difficult concepts such that you can do with an abacus such as multiplication, division, fractions, and decimals.
The easiest abacus to use to teach kids with is the Chinese abacus which has two beads on each rod on the upper deck and five beads on each rod on the lower deck. The modern abacus has one bead on each rod of the top deck and four on the lower rods—if you choose to use this you’ll have adjust your teaching methods accordingly.
First, the child must know that the beads on the far right rod on the upper deck represent two hands. Each hand of course, has five fingers. The beads on the same rod on the deck below represent individual fingers on one hand.
Show the child how to count from one to five on the lower deck by sliding one bead at a time toward the beam using something physical to count. (Toothpicks, marbles, etc. Don’t use coins at this time—that’s a different lesson and we want to avoid confusion!)
When all five beads on the lower deck have been slid toward the beam explain to the child that a bead from the top deck will now “hold” those five things place. Then slide the first bead on the upper deck toward the beam and slide all five of the beads on the lower deck away from the beam.
Explain that the five lower beads are equal to one upper bead. From here the child needs to understand that the next counting operation on that rod will begin from five. Show the child the five items counted and explain how they are represented by that single top bead.
Now count to a sum of ten and slide the second upper deck bead all the way toward the beam and slide the five lower deck beads all the way from the beam. Again show the child how the two beads represent a value of ten and compare them to the ten items you chose to use for comparison.
We are now ready to shift are value over to the “tens” rod which is to the left of the rod we have been adding on. We simply slide the first bead on that lower deck rod all the way toward the beam. Now, we reset the “ones” rod and slide those beads all the way from the beam. From here, you should keep explaining the concept of the “ones” place and the “tens” place on the abacus until the child is ready to move on to the “hundreds” and higher rods.
After a child understands how an abacus operates and can use it to count they are ready to learn the more advanced functions of the abacus.
Advanced Uses of an Abacus
Addition
Addition on the abacus is quite simple. To add the total of 22 and 13 we start with one of those numbers as our input on the abacus.
If we start with 22 then we move two beads on the “ones” rod in the lower deck all the way toward the beam. We do the same on the “tens” rod. Now we simply move three more beads in the lower deck to the beam on the “ones” rod which equals five. We now slide down one bead in the upper deck and reset the lower deck beads by sliding them away from the beam.
The carrying over function in addition works perfectly on an abacus. Let’s add 18 and 6.
We will start by sliding down a bead on the far right rod in the top deck all the way toward the beam. We then slide three beads in the lower deck on the same rod all the way toward the beam. We also slide one bead on the “tens” rod (the next rod to the left) in the lower deck all the way toward the rod. We now add six to our “ones” rod for a total of 14.
The “1” in our total belongs on our “tens” rod so we slide a second bead in the lower deck all the way towards the beam. We then reset the bead in the top deck of the “ones” rod by sliding it all the way from the beam.
We have just carried our “1.”
Now we slide one more bead on the “ones” rod in the lower deck all the ways towards the beam. We should now have two beads in the “tens” place and four beads in the “ones” place in the lower deck for a total of 24.
Subtraction
Subtraction works in exactly the opposite way by starting with the largest input number and sliding the appropriate beads away from the beam.
Multiplication & Division
Multiplication and division can also be performed with an abacus as well as functions involving fractions, decimals and negative numbers. These advanced operations are quite easy on an abacus once the technique for these operations are learned.
There is even a binary abacus which is a tool to explain how computers manipulate information.
What Type of Abacus Should I Use With My Kid?
This article assumes that you are using a Chinese abacus but you may already have or want to use one that is different.
Abaci vary in construction and there are many types and styles. The concept and use of each is very easy to grasp once you learn how to use one of any type or style. As an example, the modern abacus only has one bead on each rod in the top deck and only four beads on each rod in the bottom deck. To represent five in the top deck you simply slide the bead halfway towards the rod. Ten is represented by sliding that same bead all the way toward the beam, of course.
Again, there is no fifth bead on the bottom deck rods, so obviously you omit the step of counting to five on the bottom deck and just move the upper deck bead so that it is dead in the middle of the top of the frame and the beam. You then slide all four of the lower deck beads away from the beam and start working toward ten.
Average Cost and How to Get an Abacus
As an alternative you might shop for abacus kits. You could even fashion an abacus from most anything. You could purchase small wooden dowels, pipe cleaners and small beads from any craft store and fashion your own. Remember: abacus means “sand table” so its origins are very humble for such a powerful tool.
$15.00 is probably a very reasonable price to pay if you consider all the devices in your home that you use to make mathematical computations. An abacus consumes no electricity and doesn’t even need batteries!
The Abacus is an Effective Tool
Abaci have been used for teaching the numeral system and arithmetic in schools for many years and its presence in the classroom clearly demonstrates its importance as a teaching aid.
The ideal ages to start teaching a child how to use an abacus is between five to ten years old, but kids as early as two years old have effectively used it. Children are taught to use their fingers when learning to count and because of this, it is difficult for them to comprehend numbers beyond ten (although, in some countries, children also count their toes).
While performing mathematical computations, children do not have an abstract mental process to perform with beyond a ten digit (two hands of fingers) mental image. An abacus replaces the concrete image of hands and provides a concrete multi-digit, bead-based system as a mental image. This image greatly improves the comprehension of mathematics beyond “base ten” thinking.
Between the ages of five and ten children learn very rapidly because the neuron activity in their brains is significantly higher at these ages then it will ever be. Using an abacus for calculations stimulates the right side of the brain, which is creative and imaginative. The abacus also stimulates the left side of the brain, which is calculating and logical. Learning to use an abacus during this time is ideal because both sides of the brain develop numerous benefits such as:
Abracadabra Abacus
There are so many reasons to use an abacus to teach your child mathematics. Besides the obvious benefits mentioned above, you and your child gain quality time together in a quest to make their education important to them.
By introducing the abacus, you create the opportunity to have one on one time with your child and know how their mind is developing. This time also allows you to further educate your child on other subjects such as history, culture, and finances—because, curiosity of the abacus will lead to questions about it.
And besides, it’s fun man. Get your kid an abacus.
How To Use An Abacus To Teach Maths?
Abacus can help us in many more ways than we know.
Manjiri is a freelance writer with experience in writing on a wide range of topics, including travel, education, yoga, and children’s activities, fun and learning. She is passionate about creative wri. more
If you’re wondering how to use an abacus for performing mathematical calculations, you’ll be surprised at how versatile this instrument can be. Abacus came into existence before the calculator or computer came into existence. For the longest time, Eastern societies have used the abacus to calculate. An abacus is a rectangular wooden frame with horizontal bars that divide it into top and bottom sections. These have beads that allow for elaborate hexadecimal calculations. Addition, subtraction, or multiplication, your kid can do it all if they know the basics of an abacus. With plenty of benefits, it would be worthy of considering introducing the abacus early on. Here we are to help you with some information on how to use it so you can help them develop mental math skills.
What Is An Abacus?
The abacus, also sometimes known as a counting frame, is a calculating tool that was predominantly used in Asia and Africa. The earlier versions were made using stones or beans that moved in grooves on sand or tablets of wood, metal or stone. The modern abacus is mostly constructed in the form of a bamboo frame and has beads that have to be slid on wires.
Benefits Of Teaching The Abacus Method To Your Kid:
Here are a few ways in which learning the abacus will help your kid:
How To Make An Abacus For Kids At Home:
How To Use An Abacus For Kids: Simple Methods
All you need to teach your kid about the abacus is how to use an abacus itself. You can choose one which has two different colored beads in each row or go for a simple one in which all the beads are of the same color. Remember that before your kid learns to do more complex things on the abacus, such as addition, subtraction, multiplication or more, you will first have to teach the concept of the abacus and how to use it. Here are two simple methods with which you can help your kid to learn to use the abacus:
A Short Tutorial on How to Use An Abacus
Before computers, there were abaci (plural of abacus). They were used as a calculation tool for hundreds of years. They were popular to the Greeks, Romans, Chinese, Japanese and Koreans.
However, history tells us that there were way earlier versions of the modern abaci we know. According to Wikipedia, they existed in Sumeria as early as 2700 BC.
Parts of the Abacus
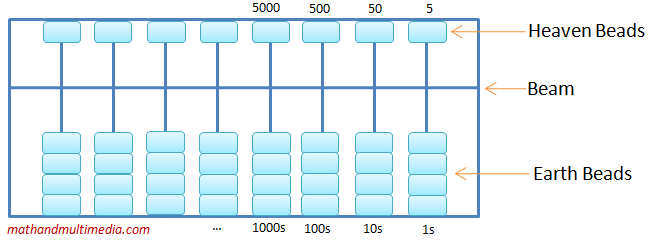
In this post, we are going to learn to use an abacus, particularly the Japanese abacus. The Japanese word for abacus is soroban. It is very similar to other abaci which consist of a frame with beads sliding on wires or rods.
A horizontal beam as shown in the figure above divides the bead into two groups. The beads at the upper part of the beam are called the Heaven Beads, while the beads below it are called Earth Beads.
How to Count Using the Japanese Abacus
Just like writing numbers, rods represent place value. Each bead in the rightmost rod is worth 1, in the next rod worth 10, the third rod is worth 100, and so on. The Heaven Bead is worth 5 times the Earth Bead. So, in the hundreds place, the Heaven Bead is worth 500 as shown above and the Earth Beads are worth 100 each. Below are several numbers represented by the Japanese abacus.
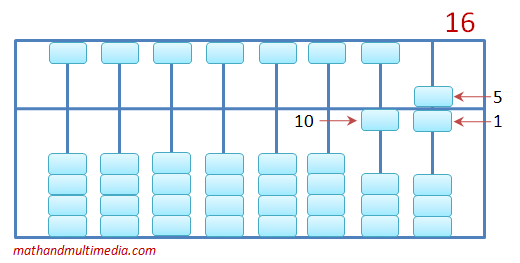
You can represent numbers using the beads by pushing them toward the beam such that the beads and the beam touch. For example, to represent 16, one way is to push 5 and 1 toward beam in the ones place and push 10 towards the beam in the tens place. If we add the value of the beads near the beam, we have 10 + 5 + 1 = 16.
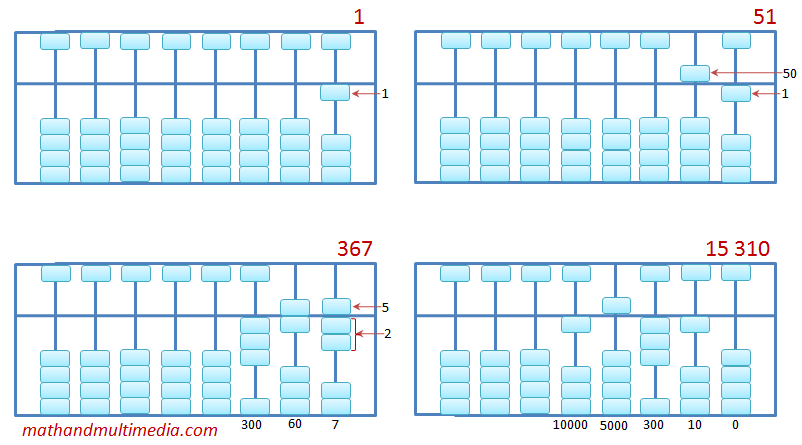
The preceding examples (click image to enlarge) show representations of different numbers. Study these representations and they should be enough for you to calculate using an abacus.