К чему стремится арктангенс бесконечности
arctg бесконечности
Здравствуйте!
Чему равен arctg бесконечности? С тригонометрией сложно у меня все, поэтому нужно подробно.
Спасибо!
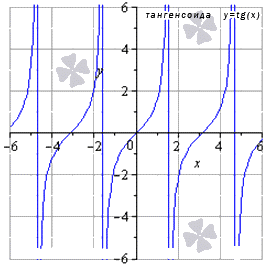
Определим, чему равен arctg бесконечности. Для этого нам понадобятся свойства функции арктангенс, а также ее график.
Арктангенс является обратной функцией к тангенсу. Следовательно, область определения арктангенса является областью значений тангенса, то есть это вся числовая прямая. А областью значений арктангенса является область определения тангенса, то есть это промежуток от –Пи/2 до Пи/2.

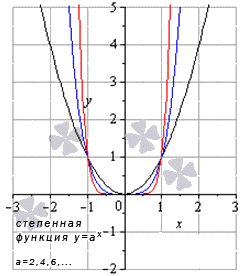
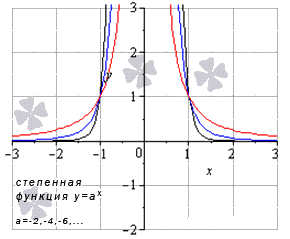
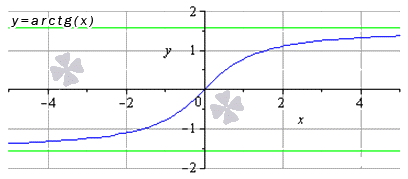
По графику функции арктангенс можно определить как ведет себя функция на бесконечности. При аргументе x, который стремится к бесконечности (точнее, к положительному значению бесконечности), функция арктангенс приближается к Пи/2. При аргументе х, который стремится к отрицательному значению бесконечности, арктангенс приближается к –Пи/2.
Следовательно, можно сделать вывод о границе арктангенса на бесконечности:
При аргументе х, стремящемся к минус бесконечности, арктангенс стремится к –Пи/2.
При аргументе х, стремящемся к плюс бесконечности, арктангенс стремится к Пи/2.
Так как на всей числовой прямой функция арктангенс является непрерывной, то граница арктангенса в любой точке равна значению arctg в данной точке: arctg 0 = 0 и т.д.
Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
arctg бесконечности равен
Здравствуйте!
Чему arctg бесконечности равен? С тригонометрией у меня все сложно, поэтому нужно подробное объяснение.
Спасибо!
Найдем ответ на вопрос: «arctg бесконечности равен». Для этого будем использовать свойства арктангенса и график этой функции.
Поскольку функция арктангенс обратна по отношению к функции тангенс, таким образом, область значений тангенса область определения арктангенса совпадают, а они равны всей числовой прямой. И наоборот, область определения тангенса совпадает с областью значений арктангенса, то есть равна значениям между –Пи/2 и Пи/2.
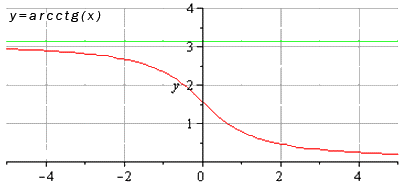
График арктангенса поможет узнать, чему будет равна функция от бесконечности:
если аргумент x будет направляться к бесконечности (более точно, к положительной бесконечности), то функция арктангенс будет все ближе к значению Пи/2;
если аргумент х будет направляться к минус бесконечности, то арктангенс будет все ближе к значению –Пи/2.
Таким образом, напрашивается следующий вывод, который можно сделать относительно границы функции арктангенс от бесконечности:
если х направляется к минус бесконечности, то арктангенс будет стремиться к –Пи/2.
если х направляется к плюс бесконечности, то арктангенс будет стремиться к Пи/2.
Функция арктангенс не прерывается на всей числовой прямой, в таком случае граница функции арктангенс в любой точке числовой прямой равна значению arctg в выбранной точке: arctg 0 = 0 и т.д.
Непосредственное вычисление пределов, таблица пределов функций
Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.
Значение предела в точке непрерывности определено значением функции в этой точке.
При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.
Произвести вычисление предела функции lim x → 5 a r c t g 3 5 · x
Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x 0 = 5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что
lim x → 5 a r c t g 3 5 · x = a r c t g 3 5 · 5 = a r c t g 3 = π 3
Для упрощения выражений применяют свойства пределов:
Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.
Таблица пределов функции
Для упрощения и решения пределов используется данная таблица основных пределов.
Функция корень n-ой степени
Для любых x 0 из опрелеления
lim x → x 0 x n = x 0 n
Функция корень n-ой степени
lim x → x 0 x n = x 0 n
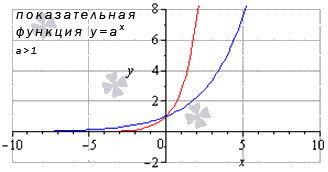
Показательная функия
Для любых x 0 из области опреления lim x → x 0 a x = a x 0
Показательная функия
Для любых знвчений x 0 из област опредения lim x → x 0 a x = a x 0
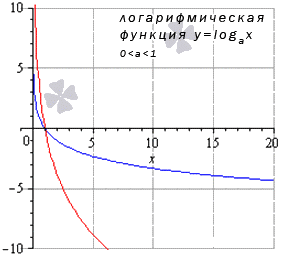
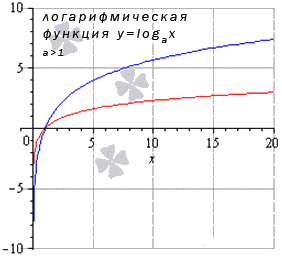
Логарифмическая функция
Для любых x 0 из области опрелеления lim x → x 0 log a x = log a x 0
Логарифмическая функция
Для любых x 0 из области опрелеления
lim x → x 0 log a x = log a x 0
lim x → ∞ t g x не существует
Для любых x 0 из области опрелеления
lim x → x 0 t g x = t g x 0
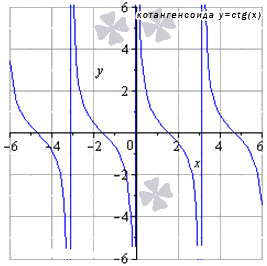
lim x → ∞ c t g x не существует
Для любых x 0 из области опрелеления
lim x → x 0 с t g x = с t g x 0
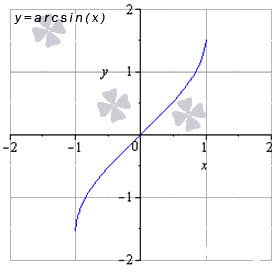
Обратные тригонометрические функции
Для любых x 0 из области опрелеления
lim x → x 0 a r c sin x = a r c sin x 0
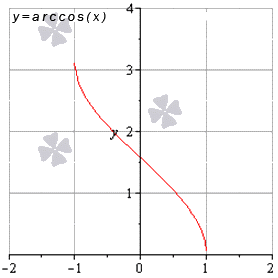
Для любых x 0 из области опрелеления
lim x → x 0 a r c c i s x = a r c cos x 0
Обратные тригонометрические функции
Для любых x 0 из области опрелеления
lim x → x 0 a r c t g x = a r c t g x 0
Для любых x 0 из области опрелеления
lim x → x 0 a r c c t g x = a r c c t g x 0
По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что
Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.
Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.
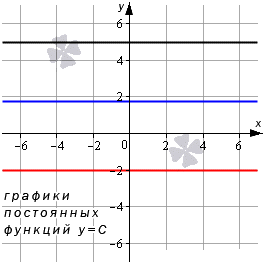
Предел константы
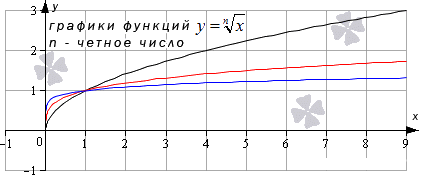
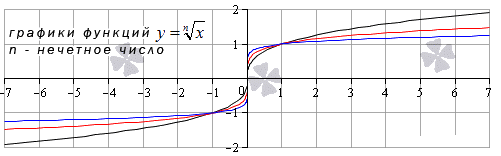
Предел функции корень n-ой степени
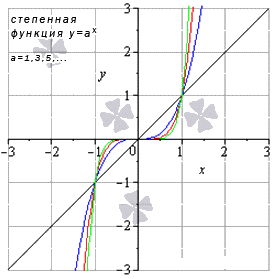
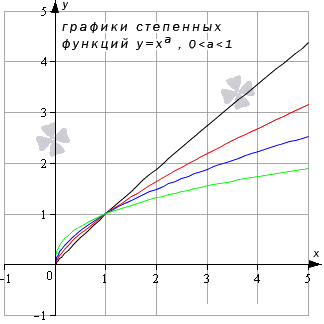
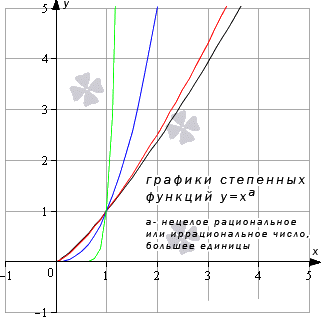
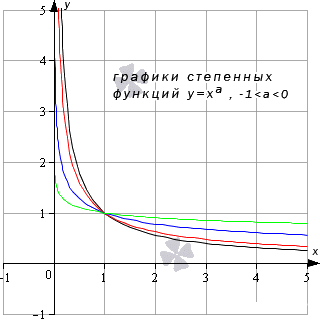
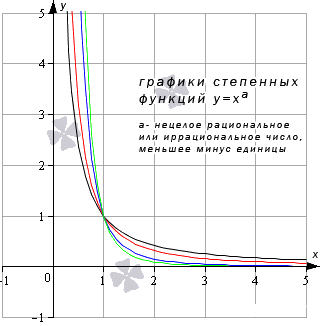
Предел степенной функции
Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.
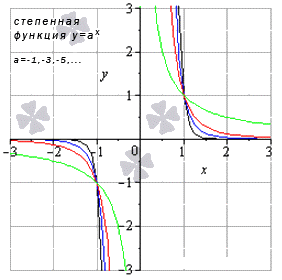
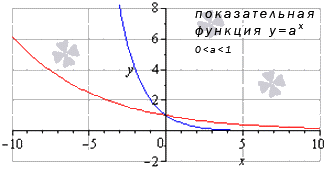
Предел показательной функции
Предел логарифмической функции
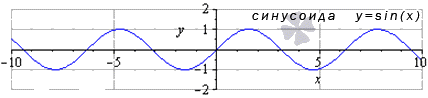
Предел тригонометрических функций
Предел обратных тригонометрических функций
Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.
Пределы с тригонометрическими функциями
Существует множество различных пределов тригонометрических функций. На помощь могут прийти основные методы вычисления:
Рассмотрим примеры подробного решения тригонометрических пределов для разбора каждого способа. Стоит отметить, что все методы можно комбинировать в одной задаче между собой для ускорения процесса вычисления.
Подставляем получившиеся преобразования, чтобы применить формулу первого замечательного предела.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Обратим внимание на корень в числителе. От него нужно избавиться путём умножения и деления на сопряженное к нему число (отличающееся знаком между слагаемыми).
Видим, что в знаменателе появился синус, а это значит, что можно избавиться от него с помощью первого замечательного предела. Как в предыдущем примере одновременно умножаем и делим на аргумент синуса.
Подставляем преобразование синуса, чтобы применить замечательный предел.
Берем производные числителя и знаменателя дроби, стоящей в показателе экспоненты.
Подставляем полученное выражение под знак предела и пременяем свойство предела для показательной функции.
Итак, в пределе неопределенность ноль делить на ноль. Выполним замены на эквивалентные функции.
Подставляем в предел и получаем готовый ответ.
Первый замечательный предел
Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.
Формула
Для применения формулы необходимо, чтобы были соблюдены два условия:
Следствия
Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.
Примеры решений
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей
В статье: «Первый замечательный предел, примеры решения» было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.