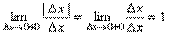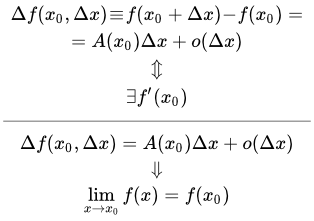Как доказать что функция дифференцируема

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

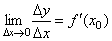
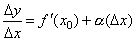
Доказательство. Если , то ,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом,из дифференцируемости функции следует ее непрерывность.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

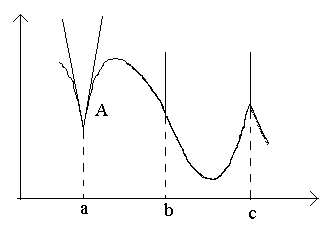
В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками. В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» c вертикальной касательной.

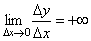
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Пример.

Покажем, что она не имеет производной в этой точке.

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

Источник

Дифференцируемые функции в точке – определение и свойства

Определение дифференцируемой функции

Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?

Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.

Свойства дифференцируемой функции

Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.

Доказательства теорем

Связь дифференцируемости функции с существованием производной

В нашем случае это означает, что
.
Отсюда
.

Связь дифференцируемости функции с ее непрерывностью

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

4.02. Дифференцируемость функции в точке и на промежутке

Производная функции, согласно ее математического определения (1.5) и (1.6) – это некий предел. Но, как и всякий предел, он может оказаться:

А) конечным; б) бесконечным; в) вообще не существовать.

Если для данного X имеет место вариант (а), то есть если при заданном X производная функции Существует и конечна, то эта функция называется Дифференцируемой в точке x.

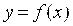
Функция, дифференцируемая в Каждой точке X некоторого промежутка оси Ох (например, интервала (A; B) или отрезка [A; B]) называется Дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее Дифференцированием (продифференцировать функцию – это значит найти ее производную).

Из геометрического смысла производной функции, определяемого равенством (1.11) и рис. 4.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции в заданной точке X:

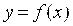
1) Существование касательной к графику функции в его точке с абсциссой X.

2) Невертикальность этой касательной (ибо не существует).

Например, функция 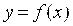, график которой изображен на рис. 4.7, не дифференцируема в точках X1, X2 и X3.

Действительно, точке X1 соответствует на графике функции точка M1 с вертикальной касательной. Точке X2 (точке максимума функции) соответствует остроконечная вершина M2, касательная в которой не существует. Точке X3 соответствует точка M3 – точка излома графика функции, в которой тоже касательная не существует.

Во всех же остальных точках M графика функции касательную к графику провести можно, и она невертикальна. Значит, для всех остальных X, отличных от (X1; X2; X3), существует производная функции. То есть во всех остальных точках X функция 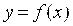дифференцируема.

Источник

Как доказать что функция дифференцируема

3.2.3. дЙЖЖЕТЕОГЙТХЕНПУФШ ЖХОЛГЙК. оЕРТЕТЩЧОПУФШ ДЙЖЖЕТЕОГЙТХЕНПК ЖХОЛГЙЙ

еУМЙ ЖХОЛГЙС ДЙЖЖЕТЕОГЙТХЕНБ Ч ЛБЦДПК ФПЮЛЕ ОЕЛПФПТПЗП ПФТЕЪЛБ [ Б ; b ] ЙМЙ ЙОФЕТЧБМБ ( Б ; b ), ФП ЗПЧПТСФ, ЮФП ПОБ ДЙЖЖЕТЕОГЙТХЕНБ ОБ ПФТЕЪЛЕ [ Б ; b ] ЙМЙ УППФЧЕФУФЧЕООП Ч ЙОФЕТЧБМЕ ( Б ; b ).

уРТБЧЕДМЙЧБ УМЕДХАЭБС ФЕПТЕНБ, ХУФБОБЧМЙЧБАЭБС УЧСЪШ НЕЦДХ ДЙЖЖЕТЕОГЙТХЕНЩНЙ Й ОЕРТЕТЩЧОЩНЙ ЖХОЛГЙСНЙ.

фБЛЙН ПВТБЪПН, ЙЪ ДЙЖЖЕТЕОГЙТХЕНПУФЙ ЖХОЛГЙЙ УМЕДХЕФ ЕЕ ОЕРТЕТЩЧОПУФШ.

еУМЙ , ФП

ЗДЕ ВЕУЛПОЕЮОП НБМБС ЧЕМЙЮЙОБ, Ф.Е. ЧЕМЙЮЙОБ, УФТЕНСЭБСУС Л ОХМА РТЙ . оП ФПЗДБ

фБЛЙН ПВТБЪПН, Ч ФПЮЛБИ ТБЪТЩЧБ ЖХОЛГЙС ОЕ НПЦЕФ ЙНЕФШ РТПЙЪЧПДОПК. пВТБФОПЕ ХФЧЕТЦДЕОЙЕ ОЕЧЕТОП: УХЭЕУФЧХАФ ОЕРТЕТЩЧОЩЕ ЖХОЛГЙЙ, ЛПФПТЩЕ Ч ОЕЛПФПТЩИ ФПЮЛБИ ОЕ СЧМСАФУС ДЙЖЖЕТЕОГЙТХЕНЩНЙ (Ф.Е. ОЕ ЙНЕАФ Ч ЬФЙИ ФПЮЛБИ РТПЙЪЧПДОПК).

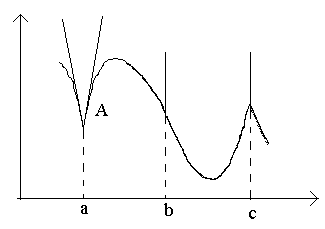
тБУУНПФТЙН ОБ ТЙУХОЛЕ ФПЮЛЙ Б, b, c.

ч ФПЮЛЕ b РТЙ ПФОПЫЕОЙЕ СЧМСЕФУС ЪОБЛПРПУФПСООПК ВЕУЛПОЕЮОП ВПМШЫПК ЧЕМЙЮЙОПК .

жХОЛГЙС ЙНЕЕФ ВЕУЛПОЕЮОХА РТПЙЪЧПДОХА. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ЧЕТФЙЛБМШОХА ЛБУБФЕМШОХА. фЙР ФПЮЛЙ – «ФПЮЛБ РЕТЕЗЙВБ» c ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК.

ч ФПЮЛЕ c ПДОПУФПТПООЙЕ РТПЙЪЧПДОЩЕ СЧМСАФУС ВЕУЛПОЕЮОП ВПМШЫЙНЙ ЧЕМЙЮЙОБНЙ ТБЪОЩИ ЪОБЛПЧ. ч ЬФПК ФПЮЛЕ ЗТБЖЙЛ ЙНЕЕФ ДЧЕ УМЙЧЫЙЕУС ЧЕТФЙЛБМШОЩЕ ЛБУБФЕМШОЩЕ. фЙР – «ФПЮЛБ ЧПЪЧТБФБ» У ЧЕТФЙЛБМШОПК ЛБУБФЕМШОПК – ЮБУФОЩК УМХЮБК ХЗМПЧПК ФПЮЛЙ.

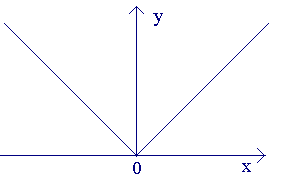
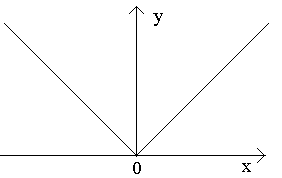
тБУУНПФТЙН ЖХОЛГЙА y=|x|.

ьФБ ЖХОЛГЙС ОЕРТЕТЩЧОБ Ч ФПЮЛЕ x = 0, Ф.Л. .

рПЛБЦЕН, ЮФП ПОБ ОЕ ЙНЕЕФ РТПЙЪЧПДОПК Ч ЬФПК ФПЮЛЕ.

оП ФПЗДБ РТЙ

б РТЙ > 0

ф.П., ПФОПЫЕОЙЕ РТЙ УРТБЧБ Й УМЕЧБ ЙНЕЕФ ТБЪМЙЮОЩЕ РТЕДЕМЩ, Б ЬФП ЪОБЮЙФ, ЮФП ПФОПЫЕОЙЕ РТЕДЕМБ ОЕ ЙНЕЕФ, Ф.Е. РТПЙЪЧПДОБС ЖХОЛГЙЙ y=|x| Ч ФПЮЛЕ x = 0 ОЕ УХЭЕУФЧХЕФ. зЕПНЕФТЙЮЕУЛЙ ЬФП ЪОБЮЙФ, ЮФП Ч ФПЮЛЕ x = 0 ДБООБС «ЛТЙЧБС» ОЕ ЙНЕЕФ ПРТЕДЕМЕООПК ЛБУБФЕМШОПК (Ч ЬФПК ФПЮЛЕ ЙИ ДЧЕ).

Источник

Дифференцируемость функции многих переменных

Частные производные.

Пусть функция
$$
f(x) = f(x_<1>, \ldots, x_)\nonumber
$$
определена в окрестности точки \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>)\). Рассмотрим функцию одной переменной
$$
\varphi (x_<1>) = f(x_<1>,x_<2>^<0>, \ldots, x_^<0>)\nonumber
$$
Функция \(\varphi (x_<1>)\) может иметь производную в точке \(x_<1>^<0>\). По определению такая производная называется частной производной \(\frac<\partial f><\partial x_<1>>(x^<0>)\).

Аналогично определяются частные производные (первого порядка)
$$
\frac<\partial f><\partial x_>(x_<1>^<0>, \ldots, x_^<0>), i = \overline<2, n>.\nonumber
$$

Функция двух переменных может иметь в точке \(x^<0>, y^<0>\) две частные производные первого порядка
$$
\frac<\partial f><\partial x>(x^<0>, y^<0>),\quad \frac<\partial f><\partial y>(x^<0>, y^<0>).\nonumber
$$

Поскольку при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функции одной переменной.

Дифференцируемость функции многих переменных в точке.

Дадим определение дифференцируемости функции в точке.

Функция \(f(x) = f(x_<1>, \ldots, x_)\) называется дифференцируемой в точке \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>)\), если она определена в некоторой окрестности этой точки и существуют такие числа \(A_<1>, \ldots, A_\), что
$$
f(x) — f(x^<0>) = \sum_ <\substack>^<\substack>A_(x_ — x_^<0>) + o(\rho(x, x^<0>)),\quad при \ x \rightarrow x^<0>.\label
$$

Функция \(f(x)\) дифференцируема в точке \(x^<0>\) в том и только том случае, когда в некоторой окрестности точки \(x^<0>\) функция \(f(x)\) может быть представлена в следующем виде:
$$
f(x) = f(x^<0>) + \sum_^f_(x)(x_ — x_^<0>)\label
$$
где функции \(f_(x)\) непрерывны в точке \(x^<0>\).

\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда выполнено условие (1). Заметим, что равенство \(\psi(x) = o(\rho(x, x^<0>))\) при \(x \longrightarrow x^<0>\) означает, что \(\psi(x) = \varepsilon(x)\rho(x, x^<0>)\), где \(\displaystyle\lim_<\substack>>\varepsilon(x) = 0\).

Доопределим функции \(\varepsilon_(x)\) в точке \(x^<0>\) по непрерывности, полагая \(\displaystyle\lim_<\substack>>\varepsilon_(x) = \varepsilon_(x^<0>) = 0\).

Показать, что функция
$$
f(x, y) = \sqrt [3] + y^<4>>\nonumber
$$
дифференцируема в точке \((0,0)\).

\(\vartriangle\) Покажем, что существует число \(C > 0\) такое, что для любых \(x \in \boldsymbol \) и \(y \in \boldsymbol \) справедливо неравенство
$$
|\sqrt [3] + y^<4>> — x| \leq C |y|^<4>\label
$$

Если \(y = 0\), то неравенство \eqref справедливо при любом \(C\). Пусть \(y \neq 0\). Положим \(t = xy^<-4/3>\). Тогда неравенство \eqref эквивалентно неравенству \(\vert \psi(t) \vert Пример 2.

Показать, что функция
$$
f(x, y) = \sqrt [3] + y^<3>>\nonumber
$$
недифференцируема в точке (0,0).

\(\triangle\) Первый способ. Пусть функция дифференцируема в точке \((0,0)\), тогда, согласно определению, существуют числа \(A\) и \(B\) такие, что
$$
f(x, y) — f(0, 0) = Ax + By + o(\rho),\quad \rho = \sqrt + y^<2>>,\nonumber
$$
где \(f(x, y) = \sqrt [3] + y^<3>>, \ f(0, 0) = 0, \ A =\displaystyle \frac<\partial f(0, 0)> <\partial x>= 1, \ B = \frac<\partial f(0, 0)> <\partial y>= 1\).

Пусть \(x = y > 0\), тогда
$$
\sqrt [3] <2>x = 2x + o(x)\nonumber
$$
или \((\sqrt [3] <2>— 2) x = o(x)\) при \(x \rightarrow 0\), что противоречит определению символа \(o(x)\). Следовательно, функция \(\sqrt [3] + y^<3>>\), недифференцируема в точке \((0, 0)\).

Второй способ. Если функция \(f(x, y)\) дифференцируема в точке \((0,0)\), то ее можно в некоторой окрестности этой точки, согласно теореме 1, представить в следующем виде:
$$
\sqrt [3] + y^<3>> = x \varphi (x, y) + y \psi (x, y),\label
$$
где функции \(\varphi (x, y)\) и \(\psi (x, y)\) непрерывны в точке \((0,0)\).

Пусть \(k\) — произвольное число. Положим в \eqref \(y = kx\). Тогда
$$
\sqrt[3]<1 + k^<3>>=\varphi(x,kx)+k\psi(x,kx).\nonumber
$$
Переходя к пределу при \(x \rightarrow 0\) и пользуясь непрерывностью функций \(\varphi (x, y)\) и \(\psi (x, y)\) в точке \((0,0)\), получаем, что при любом \(k\) выполняется равенство
$$
\sqrt [3] <1 + k^<3>> = \varphi (0, 0) + k \psi (0, 0) = a + kb.\nonumber
$$
Это неверно, так как функция \(\sqrt [3] <1 + k^<3>>\) не есть линейная функция (ее вторая производная по \(k\) не обращается тождественно в нуль). \(\blacktriangle\)

Необходимое условие дифференцируемости функции в точке.

Если функция \(f(x)\) дифференцируема в точке \(x^ <0>\in R^\), то она имеет в точке \(x^<0>\) все частные производные \(\displaystyle\frac<\partial f><\partial x_>(x^<0>),\ i = \overline<1, n>\), и
$$
f(x) — f(x^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x^<0>)(x_ — x_^<0>) + o(\rho(x, x^<0>))\quad при\ x \rightarrow x^<0>.\label
$$

\(\circ\) Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда найдутся такие числа \(A_<1>, \ldots, A_\), что при \(x \rightarrow x^<0>\) будет выполнено равенство \eqref. Пусть в этом равенстве \(x_ <1>\neq x_<1>^<0>\), а \(x_ <2>= x_<2>^<0>, \ldots, x_ = x_^<0>\). Тогда равенство \eqref принимает следующий вид:
$$
f(x_<1>, x_<2>^<0>, \ldots, x_^<0>) — f(x_<1>^<0>, \ldots, x_^<0>) = A_ <1>(x_ <1>— x_<1>^<0>) + o (|\Delta x_<1>|)\nonumber
$$
при \(x_ <1>— x_<1>^ <0>= \Delta x_ <1>\longrightarrow 0\).

Аналогично доказывается, что у функции \(f(x)\) в точке \(x^<0>\) существуют и остальные частные производные и что
$$
A_ = \frac<\partial f><\partial x_>(x^<0>),\ i = \overline<2, n>.\nonumber
$$

Подставляя эти выражения в равенство \eqref, получаем \eqref. \(\bullet\)

Так как функция \(f(x, y) = \sqrt [3] + y^<3>>\) примера 2 недифференцируема в точке \((0,0)\), то этот пример показывает, что из существования частных производных в точке не следует дифференцируемость функции в этой точке. Существование частных производных функции в точке не гарантирует даже непрерывности функции в этой точке. Так, функция
$$
f(x, y) = \begin
\displaystyle\frac<2xy> + y^<2>> & \text <при \(x^<2>+ y^ <2>> 0\)>\\
0 & \text<при \(x = y = 0\)>
\end\nonumber
$$
не имеет предела при \(x, y) \rightarrow (0, 0)\), а поэтому и не является непрерывной в точке \((0,0)\). Тем не менее у этой функции в точке \((0,0)\) существуют обе частные производные:
$$
\frac<\partial f><\partial x>(0,0) = \lim_<\substack>\frac = 0,\quad \frac<\partial f><\partial y>(0,0) = 0.\nonumber
$$

Достаточные условия дифференцируемости функции в точке.

Если все частные производные \(\frac<\partial f><\partial x_>(x),\ i = \overline<1, n>\), определены в окрестности точки \(x^ <0>\in R^\) и непрерывны в точке \(x^<0>\), то функция \(f(x)\) дифференцируема в точке \(x^<0>\).

\(\circ\) Рассмотрим случай функции трех переменных. Общий случай рассматривается аналогично. Пусть функции \(\displaystyle \frac<\partial f><\partial x>(x, y, z),\ \frac<\partial f><\partial y>(x, y, z),\ \frac<\partial f><\partial z>(x, y, z)\), определены в некотором шаре \(S_<\varepsilon>(x^<0>, y^<0>, z^<0>)\) и непрерывны в центре шара \((x^<0>, y^<0>, z^<0>)\).

Запишем приращение функции в следующем виде:
$$
f(x, y, z) — f(x^<0>, y^<0>, z^<0>) = f(x, y, z) — f(x^<0>, y, z) +\\+ f(x^<0>, y, z) — f(x^<0>, y^<0>, z) + f(x^<0>, y^<0>, z) — f(x^<0>, y^<0>, z^<0>).\nonumber
$$

Пусть \(x^ <0>0\)>\\
0, & \text<при \(x = y = 0\)>
\end\nonumber
$$
дифференцируема в точке \((0,0)\), так как
$$
f(x, y) = 0 \cdot x + 0 \cdot y + o(\sqrt + y^<2>>)\nonumber
$$
при \((x, y) \rightarrow (0, 0)\).

Но при \(x^ <2>+ y^ <2>> 0\) частная производная
$$
\frac<\partial f><\partial x>(x, y) = 2x \sin \frac<1> <\sqrt+ y^<2>>> — \frac <\sqrt+ y^<2>>> \cos \frac<1> <\sqrt+ y^<2>>>\nonumber
$$
не имеет предела при \((x, y) \rightarrow (0, 0)\) и, следовательно, не является непрерывной функцией в точке \((0,0)\). Чтобы в этом убедиться, достаточно показать, что \(\displaystyle\frac<\partial f (x, 0)><\partial x>\) не имеет предела при \(x \rightarrow 0\).

Дифференцируемость сложной функции.

Пусть функции \(\varphi_ <1>(x), \ldots, \varphi_ (x)\) дифференцируемы в точке \(x^ <0>= (x_<1>^<0>, \ldots, x_^<0>) \in R^,\ y^ <0>= (\varphi_ <1>(x^<0>), \ldots, \varphi_ (x^<0>)) \in R^\) и функция \(f(y) = f(y_<1>, \ldots, y_)\) дифференцируема в точке \(y^<0>\).

\(\circ\) Так как функция \(f(y)\) дифференцируема в точке \(y^<0>\), то в силу теоремы 1 найдутся функции \(f_(y),\ y = \overline<1, m>\), непрерывные в точке \(y^ <0>= (y_<1>^<0>, \ldots, y_^<0>)\) и такие, что
$$
f(y) — f(y^<0>) = \sum_ <\substack>^<\substack>f_(y)(y_ — y_^<0>),\quad f_(y^<0>) = \frac<\partial f><\partial y_>(y^<0>).\label
$$

Воспользовавшись тем, что дифференцируемая в точке функция непрерывна в этой точке, а также теоремой о непрерывности сложной функции, получаем, что функции
$$
\psi_ (x) = f_(\varphi_ <1>(x), \ldots, \varphi_ (x)),\quad j = \overline<1, m>,\label
$$
непрерывны в точке \(x^<0>\), причем
$$
\psi_ (x^<0>) = f_(\varphi_ <1>(x^<0>), \ldots, \varphi_ (x^<0>)) = f_(y^<0>) = \frac<\partial f><\partial y_>(y^<0>).\label
$$

Подставив в \eqref \(y_ <1>= \varphi_ <1>(x), \ldots, y_ = \varphi_ (x)\) и воспользовавшись обозначениями \eqref, получаем
$$
\Phi (x) — \Phi (x^<0>) = \sum_ <\substack>^<\substack>\psi_(x)(\varphi_ (x^<0>) — \varphi_ (x^<0>)).\label
$$

Но функции \(\varphi_ (x^<0>),\ j = \overline<1, m>\), дифференцируемы в точке \(x^<0>\), поэтому найдутся такие непрерывные в точке \(x^<0>\) функции \(\varphi_(x)\), что
$$
\begin
\displaystyle \varphi_ (x) — \varphi_ (x^<0>) = \sum_ <\substack>^<\substack>\varphi_(x)(x_ — x_^<0>),\quad \varphi_(x^<0>)=\frac<\partial \varphi_><\partial x_>(x^<0>),\\ i = \overline<1, n>,\quad j = \overline<1, m>.
\end\label
$$

Так как функции \(\psi_(x)\) и \(\varphi_(x)\) непрерывны в точке \(x^<0>\), то и функции \(\Phi_(x)\) непрерывны в точке \(x^<0>\). А это означает, что сложная функция \(\Phi(x)\) дифференцируема в точке \(x^<0>\) (теорема 1).

Вторая из формул \eqref дает правило нахождения частных производных сложной функции, аналогичное соответствующему правилу для функций одной переменной.

Пусть функция \(f(x, y)\) дифференцируема во всех точках пространства \(R^<2>\). Перейти к полярным координатам и найти выражения для \(\displaystyle\frac<\partial f><\partial r>\) и \(\displaystyle\frac<\partial f><\partial \varphi>\).

Дифференциал. Инвариантность формы первого дифференциала. Правила дифференцирования.

Пусть функция \(f(x)\) дифференцируема в точке \(x^<0>\). Тогда при \(x \rightarrow x^<0>\) ее можно записать в виде \eqref:
$$
f(x) = f(x^<0>) + \sum_ <\substack>^<\substack>\frac<\partial f(x^<0>)><\partial x_>(x^<0>)(x_ — x_^<0>) + o(\rho(x, x^<0>)).\nonumber
$$

Положим по определению
$$
dx_ = \Delta x_ = x_ — x_^<0>.\nonumber
$$

Если функция \(f(x)\) дифференцируема в точке \(x^<0>\), то линейную форму относительно приращений независимых переменных
$$
df(x^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x^<0>)dx_\label
$$
назовем дифференциалом функции \(f(x)\) в точке \(x^<0>\). Тогда
$$
f(x) = f(x^<0>) + d f(x^<0>) + o(\rho(x, x^<0>)) \ \mbox <при>\ x \rightarrow x^<0>.\nonumber
$$

Иногда выражение \eqref называют первым дифференциалом функции \(f(x)\) в точке \(x^<0>\).

Если бы \(y_<1>, \ldots, y_\) были независимыми переменными, то \(df(y^<0>)\) отличался бы от дифференциала сложной функции \eqref только тем, что в выражении \eqref \(dy_(x^<0>)\) — дифференциалы функций \(\varphi_\), а в
$$
df(y^<0>) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial y_>(y^<0>)dy_\nonumber
$$
\(dy_\) — дифференциалы независимых переменных. Формальная запись дифференциала в обоих случаях одинакова. Говорят, что форма первого дифференциала инвариантна относительно замены переменных.

Инвариантность формы первого дифференциала является весьма удобным его свойством. При записи \(df(y^<0>)\) в виде \eqref мы можем не задумываться о том, являются ли переменные \(y_<1>, \ldots, y_\) независимыми. Заметим, что во многих прикладных задачах часто бывает затруднительно выяснить вопрос о независимости переменных.

Пусть функция \(f(x)\) дифференцируема во всех точках некоторого открытого множества \(G \subset R^\). Тогда в каждой точке \(x \in G\) можно вычислить дифференциал
$$
df(x) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(y^<0>)dx_.\nonumber
$$

Он будет функцией \(2n\) переменных \(x_<1>, \ldots, x_\), \(dx_<1>, \ldots, dx_\), причем при фиксированных \(x_<1>, \ldots, x_\) дифференциал есть линейная функция \(dx_<1>, \ldots, dx_\). Правила дифференцирования такие же, как и для функций одной переменной:

Докажем, например, что \(d(uv) = u\ dv + v\ du\).

Найти дифференциал функции \(\displaystyle\operatorname\frac\).

Формула конечных приращений Лагранжа.

Пусть функция \(f(x)\) дифференцируема в выпуклой области \(G \subset R^\). Напомним, что выпуклая область есть открытое множество, любые две точки которого можно соединить отрезком, лежащим в области. Тогда для любых двух точек \(x = (x_<1>, \ldots, x_) \in G,\ y = (y_<1>, \ldots, y_) \in G\) найдется число \(\theta \in (0, 1)\) такое, что
$$
f(y) — f(x) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial y_>(x + \theta(y — x))(y_ — x_).\label
$$

Формула \eqref называется формулой конечных приращений Лагранжа. Докажем ее.

\(\circ\) Пусть точки \(x, y \in G\). Так как область \(G\) выпукла, то отрезок, соединяющий точки \(x\) и \(y\), лежит в области \(G\). Поэтому определена функция одной переменной
$$
\varphi (t) = f(x_ <1>+ t(y_ <1>— x_<1>), \ldots, x_ + t(y_ — x_)),\ 0 \leq t \leq 1.\label
$$

Очевидно, что \(\varphi (0) = f(x),\ \varphi (1) = f(y)\) и что функция \(\varphi (t)\) дифференцируема на отрезке [0,1]. По правилу нахождения производной сложной функции имеем
$$
\varphi'(t) = \sum_ <\substack>^<\substack>\frac<\partial f><\partial x_>(x_ <1>+ t(y_ <1>— x_<1>), \ldots, x_ + t(y_ — x_))(y_ — x_).\label
$$

Применим к функции \(\varphi (t)\) формулу конечных приращений Лагранжа для функции одной переменной. Получаем, что найдется число \(\theta \in (0, 1)\) такое, что \(\varphi (1) — \varphi (0) = \varphi’ (\theta)\). Используя формулы \eqref и \eqref, теперь легко получаем формулу \eqref. \(\bullet\)

Касательная плоскость к графику функции двух переменных. Геометрический смысл дифференциала.

Пусть функция \(f(x, y)\) дифференцируема на открытом множестве \(G \subset R^<2>\). Рассмотрим ее график
$$
\operatorname f = \<(x, y, z):\ z = f(x, y),\ (x, y) \in G\>.\nonumber
$$

Пусть точка \(P(x_<0>, y_<0>, z_<0>)\) лежит на \(\operatorname f\), то есть \(z_ <0>= f(x_<0>, y_<0>)\), и пусть гладкая кривая
$$
\Gamma = \\nonumber
$$
лежит на графике и проходит через точку \((x_<0>, y_<0>, z_<0>)\). Это означает, что
$$
z(t) = f(x(t), y(t));\ (x(t_<0>),\ y(t_<0>),\ z(t_<0>) = (x_<0>, y_<0>, z_<0>),\ t_ <0>\in (\alpha, \beta).\label
$$

Дифференцируя тождество \eqref в точке \(t_<0>\) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
dz = \frac<\partial f><\partial x>(x_<0>, y_<0>)dx + \frac<\partial f><\partial y>(x_<0>, y_<0>)dy.\label
$$

Вектор \(d \tau = (dx, dy, dz)\) есть касательный вектор к кривой \(\Gamma\) в точке \((x_<0>, y_<0>, z_<0>)\). Введем вектор
$$
\textbf = \left(- \frac<\partial f><\partial x>(x_<0>, y_<0>),\ — \frac<\partial f><\partial y>(x_<0>, y_<0>),\ 1\right).\label
$$

Условие \eqref означает, что вектор \(\textbf\) ортогонален к касательной к кривой \(\Gamma\) в точке \((x_<0>, y_<0>, z_<0>)\). Говорят, что вектор \(\textbf\) ортогонален к кривой \(\Gamma\) в точке \(P\). Но \(\Gamma\) — любая гладкая кривая, лежащая на \(\operatorname f\) и проходящая через точку \(P\). Поэтому вектор \(\textbf\) ортогонален к любой кривой, лежащей на \(\operatorname f\) и проходящей через точку \(P\). Он называется вектором нормали к \(\operatorname f\) в точке \(P\).

Плоскость, проходящая через точку \(P\) и ортогональная вектору нормали \(\textbf\), называется касательной плоскостью к \(\operatorname f\) в точке \(P\). Ее уравнение есть
$$
Z — f(x_<0>, y_<0>) = \frac<\partial f><\partial x>(x_<0>, y_<0>)(X — x_<0>) + \frac<\partial f><\partial y>(x_<0>, y_<0>)(Y — y_<0>).\label
$$

Прямая, проходящая через точку \(P\) и параллельная вектору \(N\), называется нормалью к \(\operatorname f\) в точке \(P\). Ее уравнение —
$$
\frac><- f_(x_<0>, y_<0>)> = \frac><- f_(x_<0>, y_<0>)> = Z — f(x_<0>, y_<0>).
$$

Найдем значение аппликаты касательной плоскости, построенной в точке \(P(x_<0>, y_<0>, z_<0>) \in \operatorname f\).

Таким образом, \(d\ f(x_<0>, y_<0>)\) есть приращение аппликаты касательной плоскости (рис. 26.1).

Рис. 26.1

Производная по направлению. Градиент.

Пусть функция \(f(x, y, z)\) определена в области \(G \subset R^<3>\), и пусть точка \(P(x_<0>, y_<0>, z_<0>) \in G\). Рассмотрим луч, проходящий через точку и параллельный направлению
$$
\textbf = (\cos \alpha, \cos \beta, \cos \gamma),\nonumber
$$
где
$$
\cos^ <2>\alpha + \cos^ <2>\beta + \cos^ <2>\gamma = 1.\nonumber
$$

Если функция \(f(x, y, z)\) дифференцируема в точке \(P(x_<0>, y_<0>, z_<0>) \in G\), то производную по направлению \(\textbf\) в этой точке можно вычислить при помощи следующей формулы:
$$
\frac<\partial f><\partial l>(x_<0>, y_<0>, z_<0>) = \left.\frac