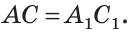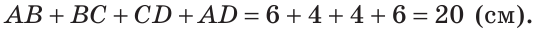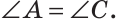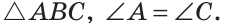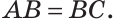Как доказать что отрезки равны геометрия 7

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения:

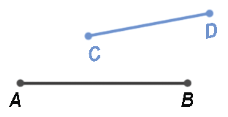
Пусть нам даны два отрезка AB и СD:

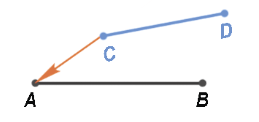
Совместим начало отрезка AB и СD (точки A и С).

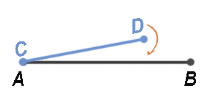
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

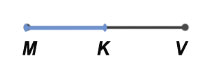
Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

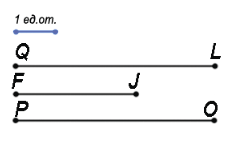
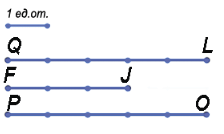
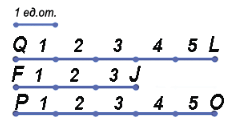
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Поделись с друзьями в социальных сетях:

Источник

Геометрия. 7 класс

Конспект урока

Решение задач на признаки равенства треугольников

Перечень рассматриваемых вопросов:

Теорема – это утверждение, справедливость которого устанавливается путём рассуждений в данной системе аксиом.

Стороны треугольника – отрезки, соединяющие вершины треугольника.

Равные треугольники – треугольники, которые можно совместить наложением.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения

В предыдущих уроках были рассмотрены различные способы определения и доказательства равенства треугольников, такие как: способ наложения, признаки равенства треугольников.

Сегодня мы будем решать задачи на вычисления и доказательство равенства треугольников.

Для успешного понимания материалов урока вспомним, какие треугольники называются равными.

‑ Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.

‑ Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.

Повторим теоремы о равенстве треугольников, так называемые признаки равенства треугольников.

1) Первый признак равенства треугольников.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2) Второй признак равенства треугольников.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

3) Третий признак равенства треугольников.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Решим задачи, используя признаки равенства треугольников.

Отрезки AB и CD – диаметры окружности с центром в точке O. Найдите периметр треугольника AOD, если отрезок CB = 13 см, а отрезок AB = 18 см.

окружность с центром O;

1) ∆AOD = ∆OBC (по первому признаку равенства треугольников).

2) Т. к. AO = OB = OC = OD = 18:2 = 9 см (как радиусы окружностей); ∠AOD = ∠COB (т. к. вертикальные углы) → CB = AD = 13 см.

3) P_∆AOD = AO + OD + AD = 9 + 9 +13 = 31 см

В четырёхугольнике ABCD, AB = CD, AD = CB, BE – биссектриса ∠B, DF – биссектриса ∠D.

Докажите, что ∠ABE = ∠ADF, ∆ABE = ∆CDF.

BE – биссектриса ∠B ∆ABС,

DF– биссектриса ∠D ∆CDА

1) ∆ABC = ∆ACD (по третьему признаку равенства треугольников).

2) Т. к. AC – общая сторона, AB = CD, AD = CB (по условию) →∠B = ∠D.

3) По условию BE – биссектриса ∠B ∆ABС, DF– биссектриса ∠D ∆CDА →∠B = ∠CBE +∠ABE = ∠ADF + ∠CDF = ∠D.

При этом ∠CBE = ∠ABE, ∠ADF = ∠CDF→∠B = 2∠ABE = 2∠ADF = ∠D→∠ABE = ∠ADF.

Т. к. AB = CD (по условию), ∠ABE = ∠ADF (доказано), ∠EAB = ∠CDF (т. к. ∆ABC = ∆ACD по третьему признаку равенства треугольников). Что и требовалось доказать.

Материал для углубленного изучения темы.

1) Приложим треугольник ∆ ABC к ∆ А₁В₁С₁, так чтобы вершина A совместилась с вершиной A₁, вершина B с B₁, вершины C и C₁ лежали по разные стороны от прямой A₁B₁.

2) Соединим точки C и C_1, так чтобы получился треугольник CC₁B.

3) Так как BC = B₁C₁, → ∆CC₁B – равнобедренный, по теореме о свойстве углов равнобедренного треугольника, →∠C = ∠С₁.

4) ∆CC₁A – также равнобедренный (по теореме о свойстве углов равнобедренного треугольника) → ∠ CС₁A = ∠С₁CA → ∠ACB = ∠AС₁B

Разбор заданий тренировочного модуля.

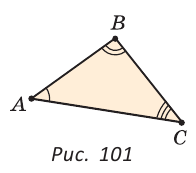
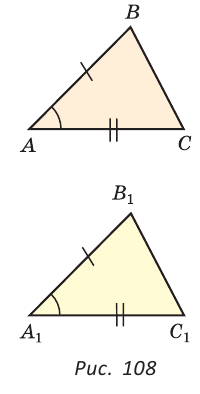
№ 1. На рисунке изображены треугольники ABD и BCD. По какому признаку, используя данные рисунка, можно доказать их равенство?

По рисунку видно, что ∠ADB = ∠DBC(углы отмечены двойной линией), ∠ABD = ∠BDC (углы отмечены одной линией), сторона DB – общая, следовательно, ∆ABD = ∆BCD (по второму признаку равенства треугольников: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны).

Ответ: используя данные рисунка, можно доказать равенство треугольников, используя второй признак равенства треугольников.

№ 2. На рисунке CD = AB, O – центр окружности. Точки A, B, C, D лежат на окружности. CD = 17 см, CO = 15 см. Найдите периметр ∆AOB.

1) Так как по условию O – центр окружности и так как точки A, B, C, D лежат на окружности, то отрезки OA = OB = OD = OC = 15 см (как радиусы окружности). CD = AB = 17 см (по условию). Периметр ∆AOB – это сумма всех его сторон.

Р_∆AOB = OA + OB + AB = 15 +15 + 17 = 47 см

Источник

Что такое аксиома, теорема и доказательство теоремы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие аксиомы

Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.

Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.

Синоним аксиомы — постулат. Антоним — гипотеза.

Основные аксиомы евклидовой геометрии

Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.

А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.

Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:

Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:

Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:

Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.

На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.

Понятие теоремы

Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.

Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.

Состав теоремы: условие и заключение или следствие.

Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.

Примеры следствий из аксиомы о параллельности прямых:

Доказательство теоремы — это процесс обоснования истинности утверждения.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.

Способы доказательства геометрических теорем

Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.

Приемы для доказательства в геометрии:

Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.

Прямая и обратная теорема взаимно-обратные. Например:

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.

Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.

Вот, как выглядит взаимное отношение теорем на примере:

В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.

Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!

Доказательство через синтез

Рассмотрим пример синтетического способа доказательства.

Теорема: сумма углов треугольника равна двум прямым.

Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.

Доказательство:

Проведем прямую DE, так чтобы она была параллельна AC.

Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.

Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.

Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.

Доказательство через анализ

Рассмотрим пример аналитического способа доказательства.

Теорема: диагонали параллелограмма пересекаются пополам.

Дан параллелограмм: ABCD.

Доказательство:

Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.

Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.

Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.

Теоремы без доказательств

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:

Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:

где a, b и c — стороны плоского треугольника,

α — угол напротив стороны а.

Следствия из теоремы косинусов:

Понятия свойств и признаков

У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.

Свойства и признаки — понятия из обычной жизни, которые мы часто используем.

Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.

Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.

Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.

Признак — это то, по чему мы однозначно распознаем объект.

Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.

А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.

Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.

Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:

Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.

Такие утверждения называют необходимым и достаточным признаком.

Источник

Содержание:

Если на плоскости отметить три точки А, В и С, не лежащие на одной прямой, и соединить их отрезками, то получим треугольник ABC. Можно сказать, что треугольник — это трехзвенная замкнутая ломаная. Обозначают:

Определения

Определение. Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.

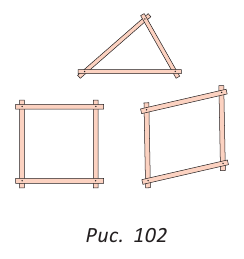
Если соединить концами три деревянных планки, то получится треугольник, который нельзя подвергнуть деформации — он будет сохранять свою форму. Тогда как четырехугольник может менять свою форму (рис. 102)? Это свойство «жесткости» треугольника широко используется в технике, производстве, строительстве.

Равные треугольники

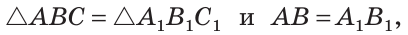
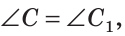
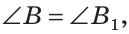
Равные треугольники можно совместить наложением так, что соответственно совпадут все три стороны и все три угла (рис. 103). В совпавших, то есть в равных треугольниках, против равных сторон лежат равные углы, а против равных углов — равные стороны. Если то а если то

Для совмещения равных отрезков достаточно совпадения их концов, а для совмещения равных треугольников — совпадения их вершин.

Виды треугольников

Если у треугольника все три стороны имеют разную длину, то такой треугольник называется разносторонним.

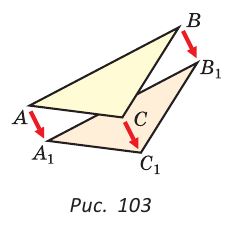
Треугольник, у которого две стороны равны, называется равнобедренным. Его равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника (рис. 104).

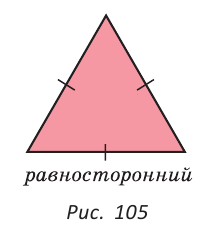
Если у треугольника равны все три стороны, то он называется равносторонним (рис. 105). Равносторонний треугольник является также и равнобедренным, где любую пару сторон можно принять за боковые стороны.

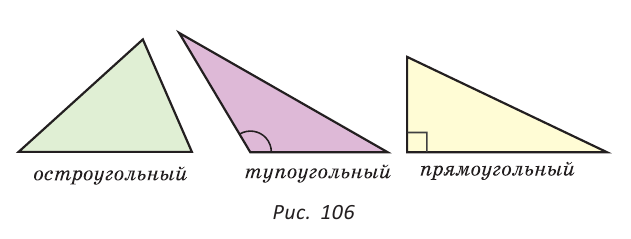
По величине углов треугольники делятся на остроугольные (у них все углы острые), тупоугольные (есть тупой угол) и прямоугольные (есть прямой угол) (рис. 106).

Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.

Периметром треугольника (многоугольника) называется сумма длин его сторон.

Равными треугольниками называются треугольники, которые можно совместить наложением.

Равнобедренным треугольником называется треугольник, у которого две стороны равны.

Равносторонним треугольником называется треугольник, у которого все стороны равны.

Свойство равных треугольников. В равных треугольниках против равных сторон лежат равные углы, а против равных углов — равные стороны.

Замечание. Называя или записывая равные треугольники, стараются соблюдать последовательность соответствующих вершин. Во многих случаях это удобно. Однако делать это необязательно. Обе записи: АВС =KNM и BAC =KNM — правильные. Иногда соответствующие вершины равных треугольников обозначают одними и теми же буквами, добавляя к буквам одного из треугольников индекс: АВС = = А₁В₁С₁. При такой записи имеют в виду, что соответствующими являются вершины А и А₁, В и В₁, С и С₁.

Первый и второй признаки равенства треугольников

При выяснении равны ли треугольники нет необходимости устанавливать равенство всех их соответствующих элементов путем наложения или измерения. Следующие две теоремы гарантируют равенство треугольников при равенстве некоторых сторон и углов.

Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

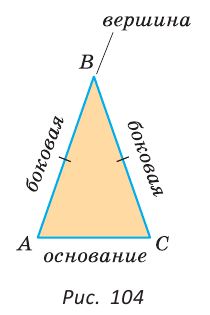
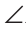
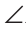
Дано: АВ =А₁В₁, АС =А₁С₁, A = A₁ (рис. 108).

Доказать: АВС = А₁В₁С₁.

Доказательство:

Наложим треугольник ABC на треугольник А₁В₁С₁ так, чтобы совпали равные углы А и А₁, луч АВ совпал с лучом А₁В₁, а луч АС совпал с лучом А₁С1. Так как отрезки АВ и А₁В₁ равны, то они совпадут при наложении, и вершина В совпадет с вершиной В₁. Аналогично совпадут равные отрезки АС и A₁C₁, вершина С совпадет с вершиной C₁. Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, АВС = А₁В₁С₁. Теорема доказана.

Говорят, что две стороны и угол между ними задают треугольник однозначно.

Теорема (второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

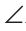
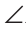
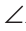
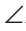
AC =А₁С₁, A = А₁, C = С₁ (рис. 109).

Доказать: АВС = А₁В₁С₁.

Доказательство:

Наложим треугольник ABC на треугольник А₁В₁С₁ так, чтобы совпали равные стороны АС и А₁С₁, угол А совпал с равным углом А₁, а угол С — с равным углом Сх. Тогда луч АВ совпадет с лучом А₁В₁, луч СВ — с лучом С₁В₁, а вершина В совпадет с вершиной В₁ (точка В будет принадлежать и прямой
А₁В₁, и прямой С₁В₁, и поэтому совпадет с точкой их пересечения В₁). Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, АВС = А₁В₁С₁. Теорема доказана.

Говорят, что сторона и два прилежащих к ней угла задают треугольник однозначно

Пример №1

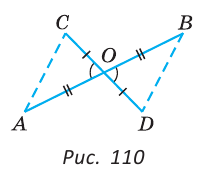
Отрезки АВ и CD пересекаются в их серединах. Доказать, что расстояния между точками А и С, В и D равны.

Доказательство:

Пусть О — точка пересечения отрезков АВ и CD (рис. 110). Рассмотрим АОС и BOD. У них АО = ОВ, CO = OD по условию, AOC = BOD как вертикальные. Треугольники равны по двум сторонам и углу между ними, то есть по 1-му признаку равенства треугольников. Стороны АС и BD равны, так как в равных треугольниках против равных углов лежат равные стороны.

Возможно краткое оформление решения задачи.

Пример №2

Решение:

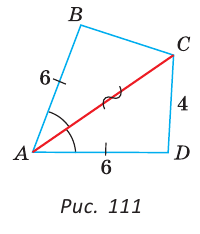
У треугольников ABC и ADC сторона АС — общая (рис. 111), AB=AD по условию, BAC =DAC, так как АС — биссектриса угла BAD.

Эти треугольники равны по 1-му признаку равенства треугольников.

Отсюда ВС = CD как соответствующие (соответственные) стороны в двух равных треугольниках.

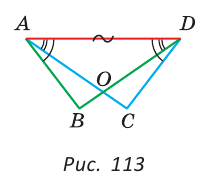
Длина ломаной ABCD:

Пример №3

На сторонах угла В отложены отрезки: ВА = ВС, КА-МС (рис. 112). Доказать, что A = С.

Доказательство:

Пример №4

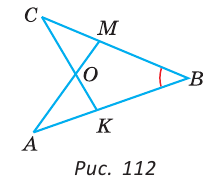
На рисунке 113 BAD = CDA, CAD = BDA. Доказать равенство треугольников АОВ и DOC.

Доказательство:

Так как ABD =DCA по 2-му признаку равенства треугольников (сторона AD — общая, углы при стороне AD соответственно равны по условию), то АВ = DC, B =C.

Высота, медиана и биссектриса треугольника

У треугольника, помимо трех сторон, трех вершин и трех углов, имеются также и другие элементы — высота, медиана и биссектриса.

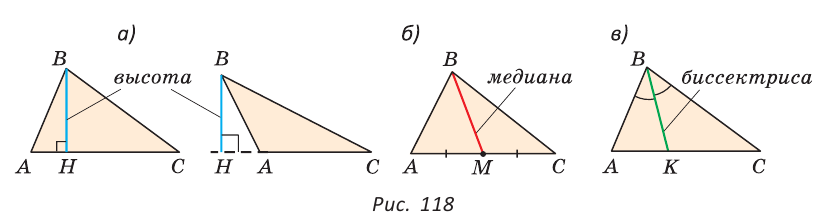
Определение. Высотой треугольника (рис. 118, а) называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на ее продолжение (отрезок ВН).

Определение. Медианой треугольника (рис. 118, б) называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны (отрезок ВМ).

Определение. Биссектрисой треугольника (рис. 118, в) называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения биссектрисы с противоположной стороной (отрезок ВК).

В равных треугольниках равны соответствующие высоты, медианы и биссектрисы.

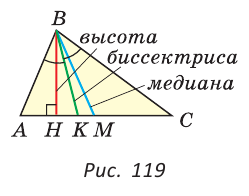
Если треугольник не равнобедренный, то высота, медиана и биссектриса, проведенные из одной вершины треугольника, не совпадают (рис. 119).

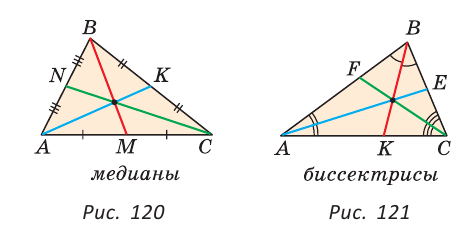
Поскольку у треугольника три вершины, то у него и три высоты, три медианы, три биссектрисы. Позже мы докажем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Это же касается медиан треугольника (рис. 120) и его биссектрис (рис. 121).

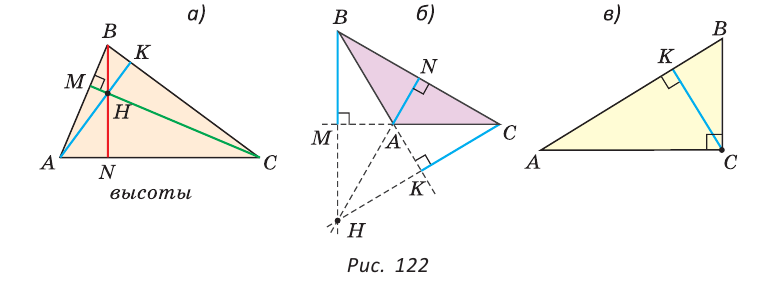
Если треугольник остроугольный (рис. 122, а), то точка пересечения его высот находится внутри треугольника ABC. Если треугольник тупоугольный или прямоугольный (рис. 122, б, в), то продолжения высот пересекаются соответственно вне треугольника или в вершине прямого угла.

Точки пересечения высот, биссектрис и медиан называются замечательными точками треугольника.

Геометрия 3D

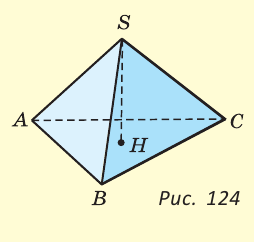
Тетраэдром или треугольной пирамидой называется многогранник, у которого все четыре грани — треугольники. Любую его грань можно принять за основание, а противолежащую вершину — за вершину пирамиды. Если точка S — вершина, а треугольник ABC — основание пирамиды, то перпендикуляр SH к плоскости ABC является высотой тетраэдра (рис. 124).

Равнобедренный треугольник

Определение. Треугольник называется равнобедренным, если у него две стороны равны.

Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника.

Рассмотрим некоторые свойства равнобедренного треугольника и один из его признаков.

Теорема (о свойстве углов при основании). В равнобедренном треугольнике углы при основании равны.

Дано: 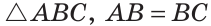(рис. 126).

Доказать:

Доказательство:

Проведем биссектрису ВК треугольника ABC. Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК — общая, АВ = ВС по условию, углы АВК и СВК равны по определению биссектрисы. Из равенства этих треугольников следует, что 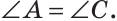Теорема доказана.

Теорема (о свойстве биссектрисы равнобедренного треугольника).

В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.

Дано: 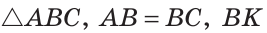— биссектриса (рис. 127).

Доказать: ВК — медиана и высота.

Доказательство:

Треугольники АВК и СВК равны по двум сторонам и углу между ними (см. предыдущую теорему). Из равенства треугольников следует, что АК=КС и 1 =2. Так как углы 1 и 2 смежные, то их сумма равна 180°, поэтому Следовательно, ВК — медиана и высота. Теорема доказана.

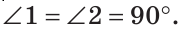
Замечание. Поскольку из вершины треугольника можно провести только одну биссектрису, одну высоту и одну медиану, то теорему можно сформулировать так: «Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают». То есть если по условию задачи дана высота равнобедренного треугольника, проведенная к основанию, то согласно данной теореме она является биссектрисой и медианой. Аналогично, если дана медиана равнобедренного треугольника, проведенная к основанию, то она является высотой и биссектрисой.

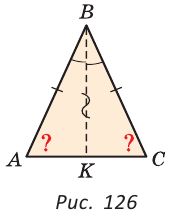
Теорема (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.

Дано:

Доказать:

Доказательство:

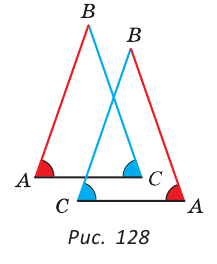
Мысленно перевернем треугольник ABC обратной стороной (рис. 128) и наложим перевернутый треугольник на треугольник ABC так, чтобы их стороны АС совпали, угол С совпал с углом А, угол А совпал с углом С.

Тогда перевернутый треугольник совместится с данным, и сторона ВС совместится со стороной АВ. Следовательно, АВ = ВС, т. е. АВС — равнобедренный. Теорема доказана.

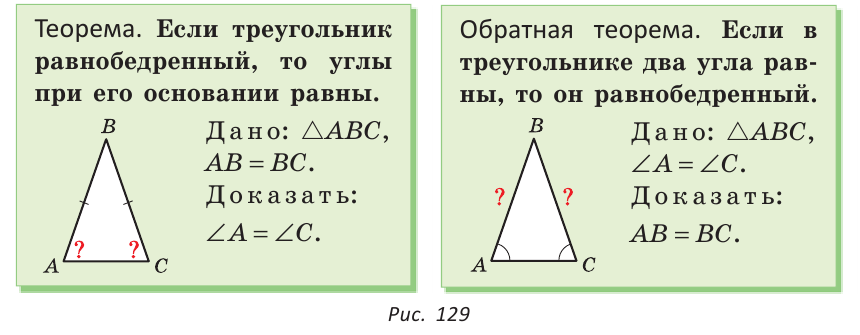
Доказанный признак равнобедренного треугольника является теоремой, обратной теореме о свойстве углов при основании равнобедренного треугольника (рис. 129).

Напомним, что любая теорема состоит из условия — того, что дано, и заключения — того, что нужно доказать. У теоремы, обратной данной, условием является заключение данной теоремы, а заключением — условие данной.

Пример №5

Доказать, что в равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

Доказательство:

Пусть в АВС АВ =ВС, АК и СМ — биссектрисы (рис. 130). Нужно доказать, что АК = СМ. Рассмотрим АКВ и СМВ. У них B — общий, АВ = ВС по условию, BAK = BCM как половины равных углов А и С при основании равнобедренного треугольника. Тогда АКВ = СМВ по 2-му признаку равенства треугольников, откуда АК = СМ. Что и требовалось доказать.

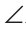
Замечание. Вторым способом доказательства будет рассмотрениеАКС иСМА и доказательство их равенства.

Пример №6

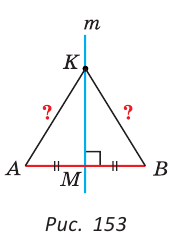
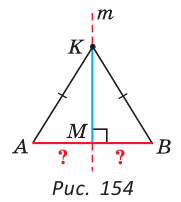
Доказать, что перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду пополам.

Доказательство:

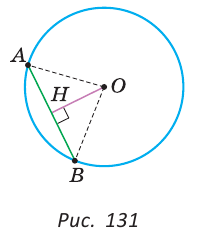
Пусть О — центр окружности, АВ — хорда, ОН — перпендикуляр к хорде АВ (рис. 131).

Отрезки OA и ОВ равны как радиусы. Поэтому треугольник АОВ — равнобедренный, а ОН — его высота, проведенная к основанию. Мы знаем, что высота равнобедренного треугольника, проведенная к основанию, является и медианой. А медиана делит сторону треугольника пополам, то есть АН = НВ. Что и требовалось доказать.

Признаки равнобедренного треугольника

Вы уже знаете один признак равнобедренного треугольника: «Если в треугольнике два угла равны, то треугольник равнобедренный». Докажем еще три признака равнобедренного треугольника, связанных с его высотой, медианой и биссектрисой.

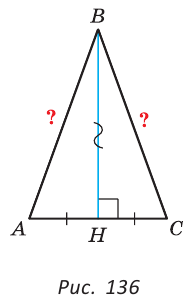
Теорема. Если в треугольнике высота является медианой, то треугольник равнобедренный.

Дано: ВН — высота и медиана АВС (рис. 136).

Доказательство:

Рассмотрим АВН и СВН. У них сторона ВН — общая, (так как ВН — высота), АН = СН (так как ВН — медиана). Треугольники АВН и СВН равны по двум сторонам и углу между ними. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.

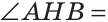
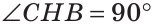
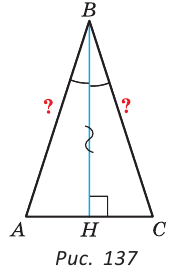
Теорема. Если в треугольнике высота является биссектрисой, то треугольник равнобедренный.

Дано: ВН — высота и биссектриса АВС.

Доказать: АВ = ВС (рис. 137).

Доказательство:

Рассмотрим АВН и СВН. У них сторона ВН — общая, (так как ВН — высота), (так как ВН — биссектриса). Треугольники АВН и СВН равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.

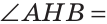
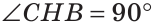
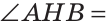
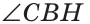
Теорема. Если в треугольнике медиана является биссектрисой, то треугольник равнобедренный.

Дано: ВМ — медиана и биссектриса АВС.

Доказать: АВ = ВС (рис. 138).

Доказательство:

Продлим медиану ВМ на ее длину за точку М. Получим МВХ = ВМ. Треугольники АМВ₁ и СМВ равны по двум сторонам и углу между ними (МВ₁ = ВМ по построению; AM = МС, так как ВМ — медиана; AMВ₁ =CMB как вертикальные). Из равенства этих треугольников следует, что АВ₁=ВС и AB₁M = =CBM. Но ZCBM = ZABM, так как ВМ — биссектриса по условию. Тогда AB₁B = ABB₁ и АВВ₁ — равнобедренный по признаку равнобедренного треугольника. Следовательно, АВ=АВ₁. А так как АВ₁=ВС, то АВ = ВС. Теорема доказана.

Замечание. Прием продления (продолжения) медианы часто используется при решении геометрических задач.

Пример №7

В треугольнике ABC с периметром 54 см медиана АК перпендикулярна стороне ВС, а высота ВМ составляет равные углы со сторонами ВА и ВС. Найти стороны треугольника ABC.

Решение:

Так как медиана АК является и высотой, то АВС — равнобедренный с основанием ВС и АВ =АС. Так как высота ВМ является и биссектрисой, то АВС — равнобедренный с основанием АС и АВ = ВС. Тогда АВС — равносторонний, (см).

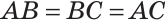
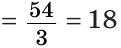
Пример №8

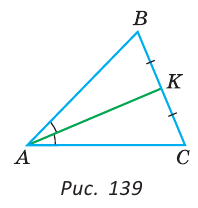
Биссектриса АК треугольника АБС делит сторону ВС пополам. Периметр треугольника ABC равен 36 см, периметр треугольника АКС равен 30 см. Найти длину биссектрисы АК.

Решение:

Из условия следует, что биссектриса АК является и медианой АВС (рис. 139).

Геометрия 3D

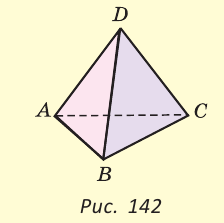
У правильной треугольной пирамиды DABC в основании лежит равносторонний треугольник ABC, а боковые грани ADB, ADC, BDC — равные равнобедренные треугольники с общей вершиной D (рис. 142).

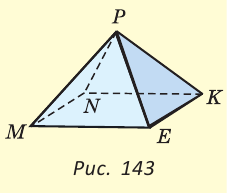
У правильной четырехугольной пирамиды в основании лежит квадрат MNKE, а боковые грани МРЕ, MPN, NPK, ЕРК — равные равнобедренные треугольники с общей вершиной Р (рис. 143).

Третий признак равенства треугольников

Вам уже известны два признака равенства треугольников. Рассмотрим еще один.

Теорема (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказать: АВС = А₁В₁С₁.

Доказательство:

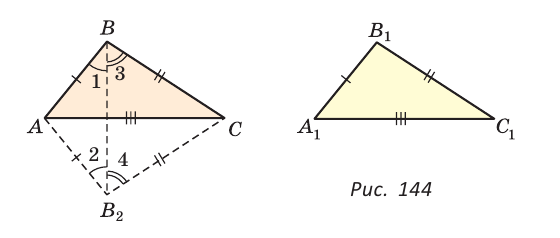
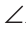
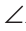
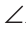
Приложим треугольник А₁В₁С₁ к треугольнику ABC так, чтобы у них совместились равные стороны А₁С₁ и АС, а вершины В₁ и В оказались в разных полуплоскостях относительно прямой АС. Треугольник А₁В₁С₁ займет положение треугольника АВ₂С. Проведем отрезок ВВ₂. Так как АВ₂=АВ и В₂С = ВС, то треугольники АВВ₂ и СВВ₂ — равнобедренные. Откуда l =2 и 3 =4 (как углы при основании равнобедренного треугольника). Тогда ABC =AB₂C, и треугольники ABC и АВ₂С равны по двум сторонам и углу между ними. Следовательно, АВС =А₁В₁С₁. Теорема доказана.

Замечание. Чтобы отрезок ВВ₂ проходил внутри треугольника ABC, следует прикладывать треугольники большей стороной.

Говорят, что три стороны задают треугольник однозначно.

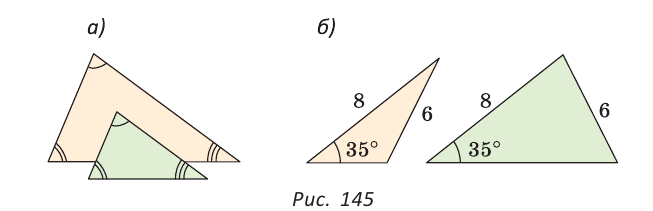
Итак, теперь вы знаете три признака равенства треугольников. Можно сформулировать и другие признаки равенства треугольников, в которых неизбежно будет присутствовать соответственное равенство каких-то трех элементов двух треугольников. Однако не любые три элемента задают треугольник. Так, например, если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники не обязательно равны. То же касается треугольников, у которых соответственно равны две стороны и угол, противолежащий одной из этих сторон.

На рисунке 145, а, б вы видите пары таких неравных треугольников.

Пример №9

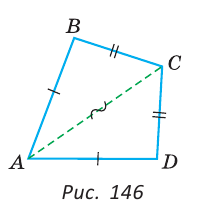
У простой замкнутой ломаной ABCD AB=AD, BC = DC. Доказать, что 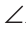B = D и луч АС — биссектриса угла BAD.

Доказательство:

Проведем отрезок АС (рис. 146).

Треугольники ABC и ADC равны по 3-му признаку равенства треугольников (AB=AD и BC = DC по условию, сторона АС — общая). Поэтому B =D и BAC =DAC как соответствующие в двух равных треугольниках и луч АС — биссектриса угла BAD.

Пример №10

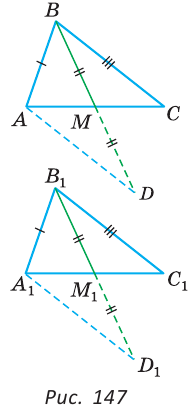
Доказать равенство треугольников по двум сторонам и медиане между ними.

Доказательство:

Нужно доказать, что АВС =А₁В₁С₁. Продлим в каждом треугольнике данную медиану на ее длину так, что MD = ВМ, M₁D₁=B₁M₁. Так как AMD =СМВ по 1-му признаку равенства треугольников (AM = МС, AMD =CMB как вертикальные, ВМ = MD по построению), то AD = BC. Аналогично AXMXDX = С₁М₁В₁, откуда A₁D₁ = B₁C₁. По условию ВС = В₁С₁, следовательно, AD=A₁D₁ и ABD =A₁B₁D₁ по трем сторонам. Тогда ABM =A₁B₁M₁ и АВМ =А₁В₁М₁ по 1-му признаку равенства треугольников. Отсюда AM =А₁М₁, АС =А₁С₁ (так как ВМ и В₁М₁ — медианы) и АВС =А₁В₁С₁ по трем сторонам.

Пример №11

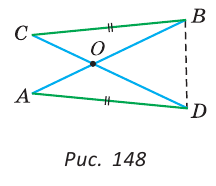
Два равных отрезка АВ и CD пересекаются в точке О и AD = BC. Доказать, что ВО = DO.

Доказательство:

Соединим точки В и D отрезком (рис. 148).

Треугольники ABD и CDB равны по трем сторонам (сторона BD — общая, AB=CD и AD=СВ по условию). Из равенства треугольников следует, что ABD =CDB. Тогда BOD — равнобедренный (по признаку равнобедренного треугольника), откуда ВО=DO.

Серединный перпендикуляр к отрезку

Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

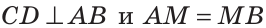
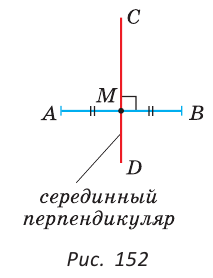
Прямая CD — серединный перпендикуляр к отрезку АВ, то есть (рис. 152).

Теорема (о серединном перпендикуляре).

Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

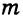
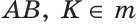
1) Дано: — серединный перпендикуляр к отрезку (рис. 153).

Доказательство:

По определению серединного перпендикуляра 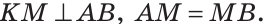Тогда в треугольнике АКВ высота КМ является медианой. По признаку равнобедренного треугольника АКВ — равнобедренный, поэтому КА=КВ.

2) Дано: 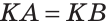(рис. 154).

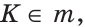
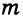
Доказать: где — серединный перпендикуляр к отрезку АВ.

Доказательство:

Проведем в равнобедренном АКВ высоту КМ, которая по свойству равнобедренного треугольника будет и медианой. Получим Прямая , проходящая через высоту КМ, — серединный перпендикуляр к отрезку АВ.

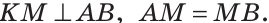
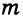
Геометрическим местом точек плоскости (или пространства) называется множество всех точек плоскости (или пространства), обладающих общим свойством.

Из доказанной теоремы следует, что серединный перпендикуляр к отрезку — это геометрическое место точек плоскости, равноудаленных от концов отрезка.

Пример №12

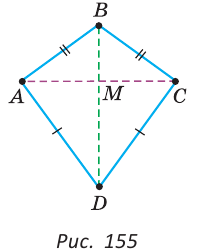
В четырехугольнике (рис. 155) ABCD AB=BC, AD=DC.

Доказать, что AC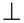BD.

Доказательство:

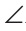
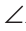
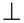
1-й способ. Из равенства треугольников ABD и CBD по трем сторонам следует, что ABD =CBD. В равнобедренном треугольнике ABC биссектриса ВМ является и высотой. Поэтому ACBD.

2-й способ. Точки В и D равноудалены от концов отрезка АС, поэтому они лежат на серединном перпендикуляре к отрезку АС. Так как через две точки проходит единственная прямая, то BD — серединный перпендикуляр к отрезку АС. Отсюда AC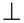BD. и AM = МС.

Пример №13 (1-я замечательная точка треугольника).

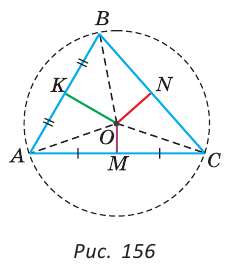
Доказать, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство:

Пусть два серединных перпендикуляра к сторонам АС и АВ пересекаются в точке О (рис. 156).

Точка О лежит на серединном перпендикуляре ОМ, поэтому ОА = ОС. Точка О лежит на серединном перпендикуляре ОК, поэтому ОА = ОВ. Отсюда ОВ = ОС. Поскольку точка О равноудалена от концов отрезка ВС, то она лежит на серединном перпендикуляре к отрезку ВС. Таким образом, третий серединный перпендикуляр пройдет через точку О, и все три серединных перпендикуляра к сторонам треугольника пересекутся в одной точке.

Напомню:

Три признака равенства треугольников:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник