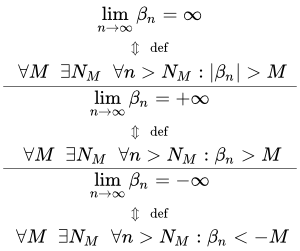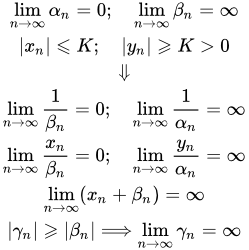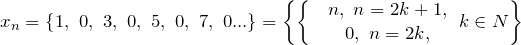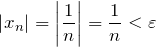Как доказать что предел последовательности равен бесконечности
Предел последовательности
п.1. Определение последовательности
С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:
Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.
Например:
1) Формула \(y_n=\frac1n,\ n\in\mathbb
2) Формула \(y_n=(-1)^n,\ n\in\mathbb
3) Рекуррентная формула \(y_1=1,\ y_2=1,\ y_(n+2)=y_(n+1)+y_n\) задает бесконечную последовательность чисел Фибоначчи:
4) Описание «число π точностью до \(10^<-n>\)» задает бесконечную последовательность все более «подробных» значений числа π:
Этот ряд можно также задать формулой \(y_n=\frac<[\pi\cdot 10^n]><10^n>\), где квадратные скобки обозначают целую часть от числа.
п.2. Предел последовательности
Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.
1) \(y_n=\frac1n\) Последовательность сходится к 0 |
2) \(y_n=(-1)^n\) Последовательность ни к чему не сходится |
3) числа Фибоначчи \(y_1=1,\ y_2=1,\ y_ Последовательность уходит на бесконечность |
4) приближения числа π Последовательность сходится к π |
п.3. Как доказать сходимость последовательности к пределу?
| \(\varepsilon\) | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 7 | 97 | 997 | 9997 | 99997 | 999997 |
| \(\lg \varepsilon\) | -1 | -2 | -3 | -4 | -5 | -6 |
| \(\lg N_<\varepsilon>\) | 0,845 | 1,987 | 2,999 | 4,000 | 5,000 | 6,000 |
И построим график (в логарифмическом масштабе):
Мы видим, что чем меньше ε, тем больше \(N_<\varepsilon>\). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно \(\lim_
Ведь для любого сколь угодно малого \(\varepsilon\gt 0\) мы можем указать такой номер \(N_<\varepsilon>=\left[\frac1\varepsilon-4\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_<\varepsilon>\) разность \(\left|\frac<1>
Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.
п.4. Ограниченные и неограниченные последовательности
п.5. Как доказать неограниченность последовательности?
Таким образом, мы доказали, что действительно \(\lim_
Ведь для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=[\sqrt
п.6. Примеры
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 15 | 128 | 1253 | 12503 | 125003 | 1250003 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac12\left(\frac<5><2\varepsilon>+3\right)\right]+1\), начиная с которого
\(\left|\frac
Что и требовалось доказать.
Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное \(N_<\varepsilon>\) немного больше «точного» значения, которое следует из исходной дроби \(\frac
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих \(y_n,\ n\geq N_<\varepsilon>\) в ε окрестности предела b.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac<1><3\sqrt<\varepsilon>>\right]\), начиная с которого \(\left|\frac
Что и требовалось доказать.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[-\log_3\varepsilon\right]\), начиная с которого \(\left|\frac<3^n+1><3^n>-1\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| \(N_<\varepsilon>\) | 2 | 362 | 39602 | 3996002 | 4·10 8 | 4·10 10 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\left(\frac<1><5\varepsilon>-1\right)^2\right]\), начиная с которого \(\left|\frac<\sqrt
Что и требовалось доказать.
Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) \( \lim_
По условию: \(y_n=2^n\)
Записываем неравенство \(|y_n|\gt M\):
\begin
Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[\log_2M\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=2^n\gt M\).
Что и требовалось доказать.
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 100 | 10 000 | 1 000 000 | 10 8 | 10 10 | 10 12 |
Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[M^2\right]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=\sqrt
Что и требовалось доказать.
Определение бесконечно большой последовательности
Определение
Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.
Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.
Окрестности бесконечно удаленных точек
Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.
Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.
Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.
С помощью логических символов существования и всеобщности, это определение запишется так:
.
Примеры бесконечно больших последовательностей
Все примеры Сначала мы рассмотрим три простых похожих примера, а затем решим более сложный.
Пользуясь определением бесконечно большой последовательности показать, что
⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Пример 2
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Пример 3
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Пример 4
Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Свойства бесконечно больших последовательностей
Формулировки свойств
Связь между бесконечно большой и бесконечно малой последовательностью
Сумма бесконечно большой и ограниченной последовательности
Произведение бесконечно большой и ограниченной снизу последовательности
Частное ограниченной и бесконечно большой последовательности
Если последовательность < βn > бесконечно большая, с неравными нулю членами, а последовательность < xn > ограничена, то
.
Доказательство ⇓
Частное ограниченной снизу и бесконечно малой последовательностью
Если абсолютные значения элементов последовательности < yn > ограничены снизу положительным числом ( | yn | ≥ K > 0 ), а < αn > – бесконечно малая с неравными нулю членами, то
.
Доказательство ⇓
Свойство неравенств бесконечно больших последовательностей
Это свойство имеет два частных случая, которые доказываются аналогичным способом.
Арифметические свойства бесконечно больших и бесконечно малых последовательностей
Приведенные выше свойства выполняются, если последовательность ограничена, а последовательность абсолютных членов ограничена снизу положительным числом. При этом эти последовательности не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти последовательности будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых последовательностей.
Доказательство свойств
Связь между бесконечно большой и бесконечно малой последовательностью
Первая часть свойства доказана.
Умножим первое неравенство (1.2) на положительное число :
.
Тогда вместо (1.2) имеем:
.
Подставим :
.
Сумма бесконечно большой и ограниченной последовательности
Произведение бесконечно большой и ограниченной снизу последовательности
Частное ограниченной и бесконечно большой последовательности
Все свойства ⇑ Если последовательность < βn > бесконечно большая, с неравными нулю членами, а последовательность < xn > ограничена, то
.
Поскольку последовательность является бесконечно большой, то, согласно свойству 1, последовательность с членами является бесконечно малой. Но произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью. См. «Произведение ограниченной последовательности на бесконечно малую». Поэтому
.
Частное ограниченной снизу и бесконечно малой последовательностью
Все свойства ⇑ Если абсолютные значения элементов последовательности < yn > ограничены снизу положительным числом ( | yn | ≥ K > 0 ), а < αn > – бесконечно малая с неравными нулю членами, то
.
Свойство неравенств бесконечно больших последовательностей
Бесконечно малые и бесконечно большие последовательности
Бесконечно большие последовательности
Следствие. Любая бесконечно большая последовательность является неограниченной.
Замечание 2. Обратное утверждение в общем случае неверно.
является неограниченной, но не является бесконечно большой. Покажем это.
Бесконечно малые последовательности
Замечание 3. Любая бесконечно малая последовательность является ограниченной, но не наоборот.
Примеры решения задач
| Задание | Доказать, что последовательность 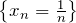 является бесконечно малой. является бесконечно малой. |
| Доказательство | Зададим произвольное положительное число  и найдем такой номер и найдем такой номер 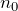 элемента этой последовательности, что для всех элемента этой последовательности, что для всех  выполняется соотношение выполняется соотношение |
Что и требовалось доказать.
Математический анализ
Записки лекций
Илья Щуров (НИУ ВШЭ)
12 Бесконечные пределы и асимптоты
12.1 Бесконечные пределы в конечных точках
12.1.1 Существование предела и ограниченность
12.1.2 Бесконечные пределы
Опять же, аналогично последовательностям, помимо просто бесконечности, бывает плюс бесконечность и минус бесконечность:
Наконец, можно рассматривать односторонние бесконечные пределы.
12.2 Пределы на бесконечности
12.2.1 Конечные пределы на бесконечности и горизонтальные асимптоты
Верный ответ. Это правда. Например, у тангенса их бесконечно много.
Неверный ответ. У функции f ( x ) = 1 / ( x ( x − 1 ) ( x + 1 ) ) их три!
Неверный ответ. Что насчёт тангенса?
Неверный ответ. Этого не может быть из определения предела по Гейне.
Неверный ответ. А что вы можете сказать про последовательность < sin ( π n ) >? Найдите несколько её членов.
Неверный ответ. Этого не может быть из определения предела по Гейне.
12.2.2 Бесконечные пределы на бесконечности
12.2.3 Наклонные асимптоты
Как искать наклонные асимптоты? На эту тему есть рецепт.
Со вторым пределом ещё проще: