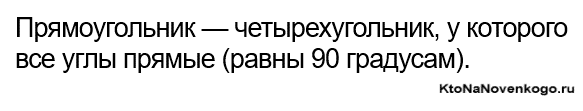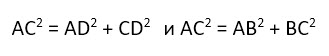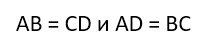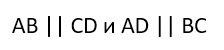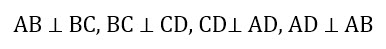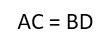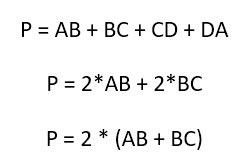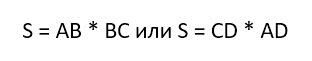Как доказать что прямоугольник это прямоугольник в окружности

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

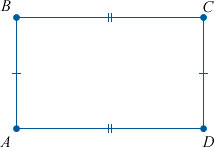
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

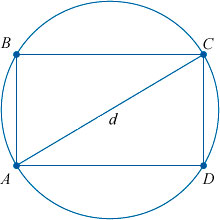
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

где \( \small a \) и \( \small b \) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем \( \small b \) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

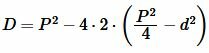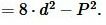(11)

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Источник

Прямоугольник

Частным видом параллелограмма является прямоугольник.

Особое свойство прямоугольника

Доказательство

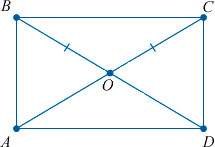
Доказать: AC = DB

Доказательство:

Теорема

Доказательство

Доказательство:

Рассмотрим ABD иACB:

Теорема

Доказательство

Доказательство:

Противолежащие углы параллелограмма равны, A = C = 90 0 и В = D = 90 0

Две теоремы, доказанные выше, называют признаками прямоугольника.

Поделись с друзьями в социальных сетях:

Источник

Прямоугольник, свойства, признаки и формулы

Прямоугольник, свойства, признаки и формулы.

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник (понятие, определение):

Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).

Прямоугольник – это четырехугольник, у которого каждый угол является прямым.

Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник

В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.

Свойства прямоугольника:

1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник

2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник

3. Стороны прямоугольника являются его высотами.

4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник

5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник

6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник

Рис. 7. Прямоугольник

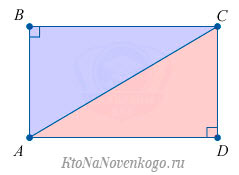
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник

9. Диагонали прямоугольника делятся точкой пересечения пополам.

10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

АС и BD – диаметр описанной окружности и диагональ прямоугольника

11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.

12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Признаки прямоугольника:

– если диагонали параллелограмма равны, то он является прямоугольником;

– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;

– если углы параллелограмма равны, то он является прямоугольником.

Формулы прямоугольника:

Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.

Формула стороны прямоугольника (длины и ширины прямоугольника):

,

,

,

.

Формула диагонали прямоугольника:

,

Формулы периметра прямоугольника:

Формулы площади прямоугольника:

Формула радиуса окружности, описанной вокруг прямоугольника:

.

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Мировая экономика

Справочники

Востребованные технологии

Поиск технологий

О чём данный сайт?

Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.

Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.

Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!

Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.

О Второй индустриализации

Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.

Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.

Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.

Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.

Источник

Прямоугольник — это одна из основ геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.

Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.

Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.

Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».

Прямоугольник — это.

Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).

У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.

То есть выглядит это так:

Так вот, прямоугольник в данном случае является частным случаем параллелограмма.

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.

У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.

Признаки прямоугольника

Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.

В случае с прямоугольником их всего три:

Диагонали прямоугольника

Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.

Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».

В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:

Свойства прямоугольника

К свойствам прямоугольника относятся следующие утверждения:

Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:

Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:

К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (5)

Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.

Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.

Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.

Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.

Источник