Как доказать что прямые перпендикулярны в призме

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Источник

Перпендикулярность прямой и плоскости (ЕГЭ 2022)

В пространстве перпендикулярными могут быть:

Давай для полного понимания рассмотрим не только перпендикулярность прямой и плоскости, а все три случая перпендикулярности в пространстве.

Все относящиеся к ним определения и формулировки теорем.

А потом обсудим очень важную теорему о трёх перпендикулярах.

И ты будешь знать о перпендикулярности в пространстве все!

Поехали!

Перпендикулярность в пространстве — коротко о главном

Перпендикулярность двух прямых

Две прямые в пространстве перпендикулярны, если угол между ними \( 90<>^\circ \).

Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.

Перпендикулярность плоскостей

Плоскости перпендикулярны, если двугранный угол между ними равен \( 90<>^\circ \).

Критерий перпендикулярности плоскостей

Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.

Теорема о трех перпендикулярах

Прямая \( a\), не лежащая в плоскости \( \alpha \), перпендикулярна прямой \( b\), лежащей в плоскости \( \alpha \), тогда и только тогда, когда проекция \( a\prime \) прямой a перпендикулярна прямой \( b\).

Перпендикулярность двух прямых

Определение:

Две прямые в пространстве перпендикулярны, если угол между ними \( \displaystyle 90<>^\circ \).

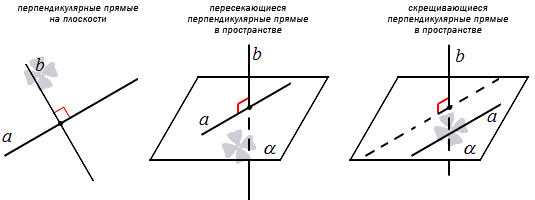
Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.

На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):

А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:

Прямая \( \displaystyle a\) перпендикулярна прямой \( \displaystyle b\), хотя и не пересекается с нею. Как так?

Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми \( \displaystyle a\) и \( \displaystyle b\), нужно через произвольную точку \( \displaystyle O\) на прямой a провести прямую \( \displaystyle ’\parallel b\).

И тогда угол между \( \displaystyle a\) и \( \displaystyle b\) (по определению!) будет равен углу между \( \displaystyle a\) и \( \displaystyle <’>\).

Вспомнили? Ну вот, а в нашем случае – если окажутся перпендикулярны прямые \( \displaystyle a\) и \( \displaystyle <’>\), то нужно считать перпендикулярными прямые \( \displaystyle a\) и \( \displaystyle b\).

Для полной ясности давай рассмотрим пример

Эти прямые не пересекаются – они скрещиваются. Чтобы найти угол между \( \displaystyle AC\) и \( \displaystyle <_<1>><_<1>>\), проведём \( \displaystyle BD\).

Из-за того, что \( \displaystyle B<_<1>><_<1>>D\) — параллелограмм (и даже прямоугольник!), получается, что \( \displaystyle <_<1>><_<1>>\parallel BD\).

А из-за того, что \( \displaystyle ABCD\) – квадрат, выходит, что \( \displaystyle AC\bot BD\). Ну, и значит \( \displaystyle AC\bot <_<1>><_<1>>\).

Перпендикулярность прямой и плоскости

Определение:

Прямая \( \displaystyle h\) перпендикулярна плоскости \( \displaystyle \alpha \), если она перпендикулярна всем-всем прямым в этой плоскости: и \( \displaystyle a\), и \( \displaystyle b\), и \( \displaystyle c\), и даже \( \displaystyle d\)!

И ещё миллиарду других прямых!

Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит!

Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Если найдутся всего лишь две пересекающиеся прямые (\( \displaystyle a\) и \( \displaystyle b\)) в плоскости \( \displaystyle\alpha\), которым перпендикулярна прямая \( \displaystyle h\), то эта прямая сразу окажется перпендикулярна плоскости \( \displaystyle \alpha \),

То есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой \( \displaystyle c\)).

Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.

Что это за арка? Это значок «пересечение»! Хороший способ быстрее писать конспекты 🙂

Прямая перпендикулярна двум пересекающимся прямым!

И опять рассмотрим пример

Пусть нам дан правильный тетраэдр \( \displaystyle ABCD\).

Задача: доказать, что \( \displaystyle BD\bot AC\).

Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!

Давай отметим середину \( \displaystyle M\) ребра \( \displaystyle AC\) и проведём \( \displaystyle BM\) и \( \displaystyle DM\).

Это медианы в \( \displaystyle \Delta ABC\) и \( \displaystyle \Delta ADC\).

Треугольники – правильные \( \displaystyle \Rightarrow BM\bot AC\) и \( \displaystyle DM\bot AC\).

Вот оно, чудо: получается, что \( \displaystyle AC\bot BMD\), так как \( \displaystyle AC\bot BM\) и \( \displaystyle AC\bot DM\).

И далее, \( \displaystyle AC\bot BMD\Rightarrow AC\bot \) всем прямым в плоскости \( \displaystyle BMD\), а значит, и \( \displaystyle AC\bot BD\).

И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.

Перпендикулярность плоскостей

Определение:

Плоскости перпендикулярны, если двугранный угол между ними равен \( \displaystyle 90<>^\circ \).

То есть (подробнее смотри в теме «двугранный угол») две плоскости (\( \displaystyle \alpha\) и \( \displaystyle \beta\)) перпендикулярны, если окажется, что угол между двумя перпендикулярами (\( \displaystyle a\) и \( \displaystyle b\)) к линии пересечения этих плоскостей равен \( \displaystyle 90<>^\circ \).

И есть теорема, которая связывает понятие перпендикулярных плоскостей с понятием перпендикулярность в пространстве прямой и плоскости.

Теорема эта называется: Критерий перпендикулярности плоскостей.

Критерий перпендикулярности плоскостей

Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.

Как всегда, расшифровка слов «тогда и только тогда» выглядит так:

(естественно, здесь \( \displaystyle \alpha \) и \( \displaystyle \beta \) — плоскости).

Теорема о трёх перпендикулярах

Эта теорема – одна из самых важных в стереометрии, но, к сожалению, и одна из самых непростых в применении.

Так что нужно быть очень внимательным!

Прямая \( \displaystyle a\), не лежащая в плоскости \( \displaystyle \alpha \), перпендикулярна прямой \( \displaystyle b\), лежащей в плоскости \( \displaystyle \alpha \), тогда и только тогда, когда проекция \( \displaystyle <’>\) прямой a перпендикулярна прямой \( \displaystyle b\).

И снова расшифровка слов «тогда и только тогда». Теорема утверждает сразу две вещи (смотри на картинку):

Давай попробуем применить эту теорему для решения задачи.

Задача: дана правильная шестиугольная пирамида \( \displaystyle SABCDEF\). Найти угол между прямыми \( \displaystyle AS\) и \( \displaystyle CE\).

Решение:

Из-за того, что в правильной пирамиде вершина при проекции попадает в центр основания, оказывается, что прямая \( \displaystyle AD\) — проекция прямой \( \displaystyle AS\).

Но мы знаем, что в правильном шестиугольнике \( \displaystyle AD\bot CE\). Применяем теорему о трёх перпендикулярах:

\( \displaystyle AD\bot CE\Rightarrow AS\bot CE\)

И пишем ответ: \( \displaystyle 90<>^\circ \).

Источник

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Решение

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Источник

Как доказать что прямые перпендикулярны в призме

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Стереометрия. Страница 3

Главная > Учебные материалы > Математика: Стереометрия. Страница 3

1.Перпендикулярность прямых в пространстве. 2.Признак перпендикулярности прямой и плоскости. 3.Теорема о трех перпендикулярах. 4.Признак перпендикулярности плоскостей. 5.Расстояние между скрещивающимися прямыми. 6.Примеры.

1. Перпендикулярность прямых в пространстве

Теорема. Если две пересекающиеся прямые параллельны двум перпендикулярным прямым, то они перпендикулярны и между собой.

Рис. 1 Перпендикулярность прямых в пространстве.

2.Признак перпендикулярности прямой и плоскости

Теорема. Прямая, перпендикулярная двум пересекающимся прямым на плоскости, перпендикулярна данной плоскости.

Доказательство. Пусть прямые k и b две пересекающиеся прямые на плоскости α. Прямая а перпендикулярна прямым k и b. Доказать, что прямая а перпендикулярна плоскости α. (Рис.2)

Проведем произвольную прямую х от точки А и прямую АВ, которая пересечет прямые k и b в точках К и В на плоскости α. Отложим на прямой а два равных отрезка в разные стороны АА’ и AA». Тогда треугольники АА’K и AA»K будут равны по двум сторонам и углу между ними. Так же как и треугольники АА’В и AA»В. Отсюда следует, что треугольники А’BK и А»BK равны по третьему признаку равенства треугольников. И следовательно, треугольники А’BE и A»BE равны, т.к. одна сторона у них общая ВЕ, стороны А’B и А»B равны из предыдущих рассуждений. Углы между этими сторонами также равны. Следовательно мы приходим к выводу, что треугольники А’AE и A»AE равны по трем сторонам. АЕ является медианой, биссектрисой и высотой, так как стороны А’Е и A»Е у них равные. И следовательно, угол между сторонами АА’ и АЕ равен 90°. Это значит, что прямая а перпендикулярна плоскости α.

Рис.2 Признак перпендикулярности прямой и плоскости

3. Теорема о трех перпендикулярах

Теорема: если прямая, проведенная на плоскости и проходящая через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной.

Доказательство.

Проведем прямую через основание наклонной AD и параллельную прямой СВ. Тогда прямая AD также перпендикулярна плоскости α и соответственно прямой а. Проведем плоскость β через прямые АD и CB. Тогда, если прямая а перпендикулярна проекции наклонной АВ, то она перпендикулярна плоскости β. А следовательно, любой прямой в этой плоскости, т.е. самой наклонной АС.

Следует отметить, что верно и обратное утверждение. Если прямая, проведенная на плоскости через основание наклонной ей перпендикулярна, то она перпендикулярна и проекции наклонной на эту плоскость.

Рис. 3 Теорема отрех перпендикулярах.

4. Признак перпендикулярности плоскостей

Теорема: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярна их прямой пересечения и пересекает их по перпендикулярным прямым.

Пусть даны две плоскости α и β, которые пересекаются по прямой с (Рис.4). Проведем плоскость γ, которая пересекает плоскости α и β по прямым а и b. Плоскость γ перпендикулярна прямой с. Прямые а и b также перпендикулярны прямой с. Следовательно плоскости α и β перпендикулярны.

Если взять другую плоскость, параллельную плоскости γ, например плоскость γ’, которая пересекает прямую с под прямым углом, она пересечет плоскости α и β по прямым a’ и b’, которые будут параллельны прямым а и b. По теореме о перпендикулярности прямых в пространстве прямые a’ и b’ также будут перпендикулярны, как и прямые а и b. Что и требовалось доказать.

Рис. 4 Признак перпендикулярности плоскостей.

Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Проведем через точку А на плоскости α прямую b, перпендикулярную прямой а. Через прямые b и с проведем плоскость γ. Она перпендикулярна прямой а, так как прямая а перпендикулярна двум прямым b и с. Тогда плоскость β пересекает две плоскости α и γ по двум перпендикулярным прямым а и с. И пересекает прямую пересечения b под прямым углом. Следовательно плоскости α и β перпендикулярны.

Рис. 4.1 Перпендикулярность плоскостей.

5. Расстояние между скрещивающимися прямыми

Теорема. Две скрещивающиеся прямые имеют только один общий перпендикуляр, который также является перпендикуляром между параллельными плоскостями, проведенными через эти прямые.

Доказательство. Пусть а и b две скрещивающиеся прямые (Рис.5). Проведем через них две плоскости α и β, параллельные друг другу. А от прямой а проведем перпендикуляры на плоскость β. Таким образом, получим плоскость γ, которая перпендикулярна обоим плоскостям α и β и пересекает плоскость β по прямой a’. Прямые а и a’ параллельны. Прямая a’ пересекает прямую b в точке А. Следовательно, один из перпендикуляров, проведенных от каждой точки прямой а на плоскость β, т.е. отрезок АВ и есть общий перпендикуляр между прямыми а и b.

Допустим, что существует еще один общий перпендикуляр между прямыми а и b это CD. Тогда два перпендикуляра пересекают прямые а и b в точках А,В,С,D, которые в свою очередь параллельны между собой. Следовательно через них можно провести плоскость. А в этой плоскости лежат и две прямые а и b, которые также будут параллельны между собой. А это противоречит условию, т.к. прямые а и b являются скрещивающимися. Следовательно у двух скрещивающихся прямых может быть только один общий перпендикуляр.

Отсюда следует, что расстояние между двумя скрещивающимися прямыми равно длине их общего перпендикуляра.

Рис. 5 Расстояние между скрещивающимися прямыми.