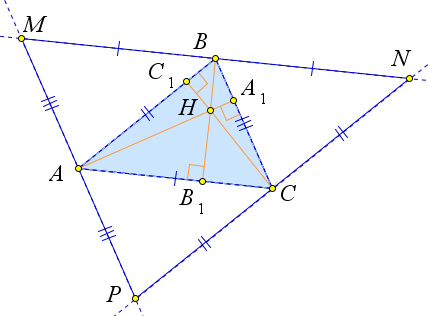
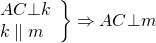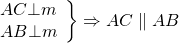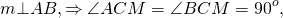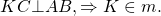Как доказать что серединные перпендикуляры пересекаются в одной точке
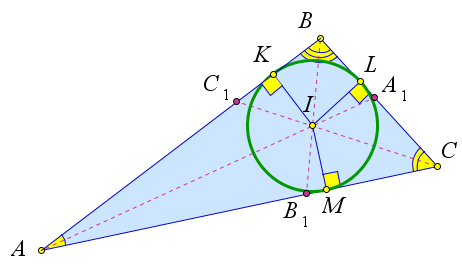
Серединные перпендикуляры к сторонам треугольника
Свойство серединных перпендикуляров к сторонам треугольника
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Д ано:
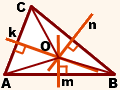
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
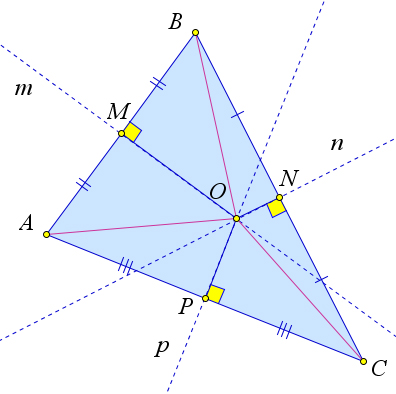
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
Что и требовалось доказать.
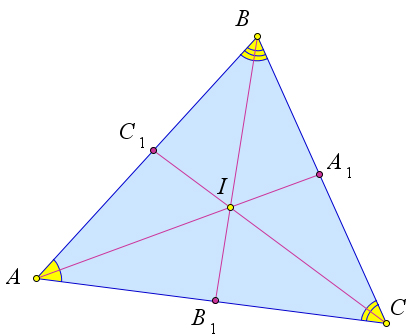
Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной около этого треугольника окружности
Точка пересечения серединных перпендикуляров к сторонам треугольника — одна из четырех замечательных точек треугольника.
Инструменты пользователя
Инструменты сайта
Содержание
Четыре замечательные точки треугольника
Определение
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в таком случае называется описанным.
Определение
Окружность называется описанной около многоугольника, если она проходит через все его вершины. Многоугольник в таком случае называется вписанным в данную окружность.
Определение
Точка пересечения медиан треугольника называется центроидом или центром масс.
Замечение
Медианы треугольника пересекаются в одной точке по теореме.
Теорема о биссектрисе, как ГМТ
Биссектриса неразвернутого угла – это геометрическое место точек, равноудаленных от его сторон.
Доказательство
Докажем, что любая точка, принадлежащая биссектрисе равноудалена от сторон этого угла.
Обратно: докажем, что если точка равноудалена от сторон угла, то она лежит на биссектрисе.
Теорема
Биссектрисы треугольника пересекаются в одной точке.
Доказательство
Первый способ.
Второй способ.
Докажем, что все биссектрисы пересекаются в одной точке.
Следствие
В любой треугольник можно вписать окружность, центром которой будет являться точка пересечения его биссектрис. Такая окружность единственна.
Доказательство
Докажем, что такая окружность единственна.
В самом деле, допустим, что в треугольник можно вписать две окружности.
Следовательно, эти окружности совпадают.
Следствие
Если все биссектрисы выпуклого многоугольника пересекаются в одной точке, то в него можно вписать окружность, центром которой будет точка пересечения биссектрис.
Доказательство
Если все биссектрисы пересекаются в одной точке, то эта точка будет равноудалена от всех её сторон, то есть перпендикуляры к сторонам многоугольника будут равны, а окружность с центром в этой точке и с радиусом, равным расстоянию от точки пересечения биссектрис до стороны, будет касаться всех сторон.
Теорема о серединном перпендикуляре, как ГМТ
Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.
Доказательство
Докажем, что любая точка, принадлежащая серединному перпендикуляру, равноудалена от сторон.
Обратно, докажем, что любая точка равноудалённая от сторон, принадлежит серединному перпендикуляру.
Следствие
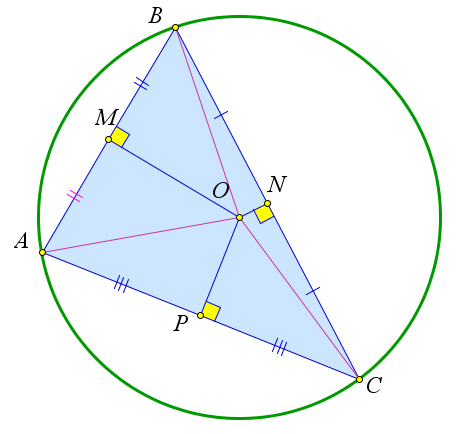
Все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Доказательство
Докажем, что эти серединные перпендикуляры пересекаются в одной точке.
Следствие
Около любого треугольника можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров к его сторонам. Такая окружность единственна.
Доказательство
Докажем, что такая окружность единственна.
Предположим, что в треугольник можно вписать две окружности.
Тогда, центры этих окружностей равноудалены от вершин треугольника.
Но такая точка только одна – это точка пересечения серединных перпендикуляров.
Следствие
Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то около него можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров.
Доказательство
Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то эта точка равноудалена от всех его вершин, и, следовательно, окружность с центром в этой точке и с радиусом, равным расстоянию от этой точки до какой-либо из его вершин, будет описанной около этого многоугольника.
Теорема
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство
Докажем, что все высоты пересекаются в одной точке.
Следствие
Следствие
Серединные перпендикуляры треугольника являются высотами серединного треугольника. Следовательно, ортоцентр серединного треугольника является центром окружности, описанной около исходного треугольника.
Доказательство
Утверждение полностью следует из доказательства теоремы.
Определение
Точка пересечения высот треугольника называется ортоцентром треугольника.
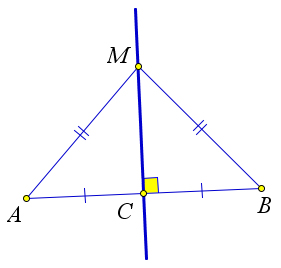
Свойства серединного перпендикуляра
Рассмотрим свойства серединного перпендикуляра. Начнем со свойства серединного перпендикуляра к отрезку.
I) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
II) И обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
I)
AB- отрезок, C — середина AB,
m — серединный перпендикуляр к AB,
1. Если точка M совпадает с точкой C.
Так как AC=BC по условию, то и AM=BM.
2. Если точка M не совпадает с точкой C.
Рассмотрим треугольники ACM и BCM
то есть треугольники ACM и BCM — прямоугольные.
AC=BC (по условию), CM — общий катет.
Из равенства треугольников следует равенство соответствующих сторон: AM=BM.
Что и требовалось доказать.
II) Дано: AB — отрезок, C — середина AB,
m — серединный перпендикуляр к AB,
Так как AK=BK (по условию), то треугольник AKB — равнобедренный с основанием AB (по определению). Так как C — середина AB, то KC — медиана треугольника AKB.
По свойству равнобедренного треугольника медиана, проведенная к основанию, является также его высотой, то есть
Что и требовалось доказать.
Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.
В следующий раз рассмотрим свойство серединных перпендикуляров к сторонам треугольника.
Докажите что серединные перпендикуляры к сторонам треугольника
Здравствуйте!
На зачете было задание «Докажите что серединные перпендикуляры к сторонам треугольника…». Дальше не помню. Кто знает что там дальше и как это доказать? Срочно нужно!
Спасибо!
Докажем, что серединные перпендикуляры к сторонам треугольника будут пересекаться в одной точке.
Данное свойство серединных перпендикуляров будем доказывать от противоположного.
Доказательство.
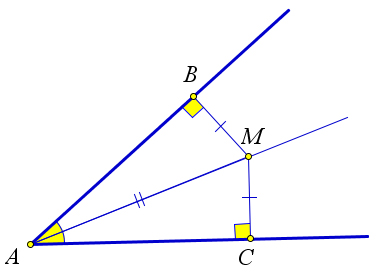
Рассмотрим произвольный треугольник NRP. Точкой M сторона NR делится пополам, а точкой S — сторона RP.
Проведем к его боковым сторонам NR и RP перпендикуляры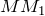 
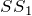
и 
. Данные перпендикуляры пересекутся в точке О.
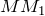
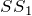
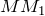
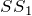
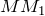
Предположим, что перпендикуляры и не пересекутся. Это значит, что они параллельны. В таком случае прямая RN, которая перпендикулярна прямой , будет перпендикулярной и к прямой , которая параллельна .
Это невозможно, так как тогда через точку R должны проходить две прямые RN и RP, которые перпендикулярны к прямой .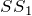
Так как любая точка серединного перпендикуляра, проведенного к стороне, равноудалена от его вершин, то ON=OR и OR=OP. Из этого следует, что ON=OP, что означает равноудаленность точки О от концов стороны NP. Таким образом, все три серединных перпендикуляра, проведенных к сторонам произвольного треугольника NRP, пересекаются в одной точке, что и требовалось доказать.
Доказательство завершено.
Серединный перпендикуляр к отрезку:
Рассмотрим понятие серединного перпендикуляра к отрезку.
Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Следующая теорема характеризует свойства точек серединного перпендикуляра к отрезку.
Теорема 5 (о серединном перпендикуляре). Каждая точка серединного перпендикуляра к отрезку находится на равном расстоянии от концов этого отрезка. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
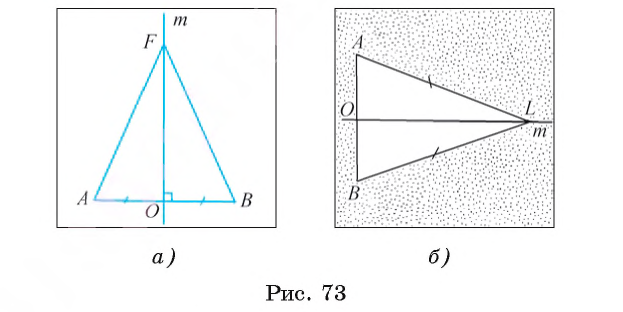
1) Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина отрезка АВ (рис. 73, а).
Пусть точка F — произвольная точка серединного перпендикуляра. Докажем, что FА = FВ. Если точка F совпадает с точкой О, то это равенство верно, так как точка О — середина отрезка АВ. Пусть точка F не совпадает с точкой О. В этом случае треугольник АОF равен треугольнику ВОF по первому признаку равенства треугольников (АО = ОВ по условию, сторона ОF — общая, 
90°). Отсюда следует, что АF = ВF.
2) Пусть точка L равноудалена от концов отрезка АВ, т. е. АL = ВL (рис. 73, б). Докажем, что точка L лежит на прямой m. Если точка L лежит на прямой АВ, то она совпадает с серединой О отрезка АВ, т. е. лежит на прямой m. Если точка В не лежит на прямой АВ, то треугольник АLВ равнобедренный. Отрезок LO — медиана этого треугольника, а следовательно, и высота. Таким образом, LО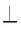
АВ, а, значит, прямые LО и m совпадают. Отсюда вытекает, что точка L лежит на прямой m.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.