Как

Как доказать что треугольник вписанный в окружность

19.01.202314.02.2023 admin 0 Comments

Окружность, вписанная в треугольник. Теоремы и их рассмотрение

Вам будет интересно: Казахская академия спорта и туризма. Факультеты, структура вуза

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:

В треугольник можно вписать только одну окружность.

Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:

Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.

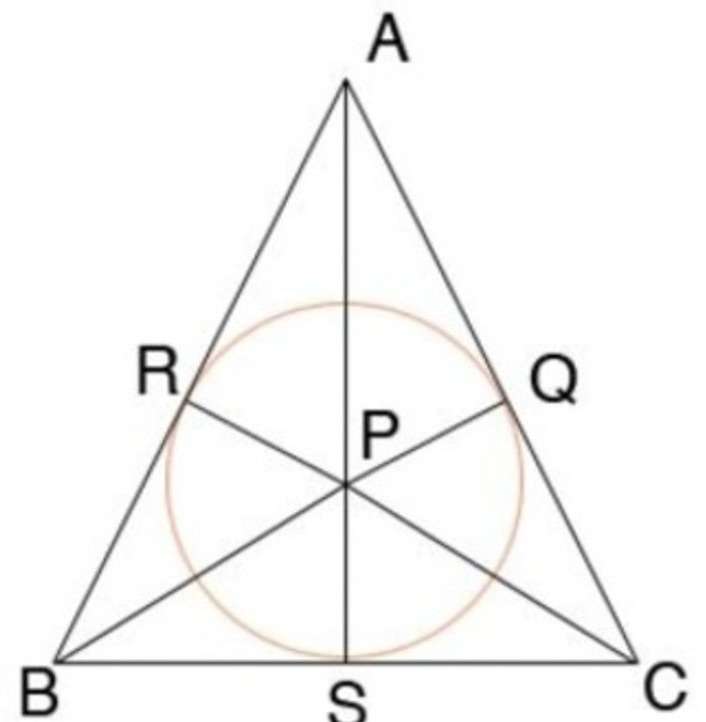
Окружность, вписанная в равнобедренный треугольник

Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.

Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).

Свойства теоремы об окружности, вписанной в треугольник:

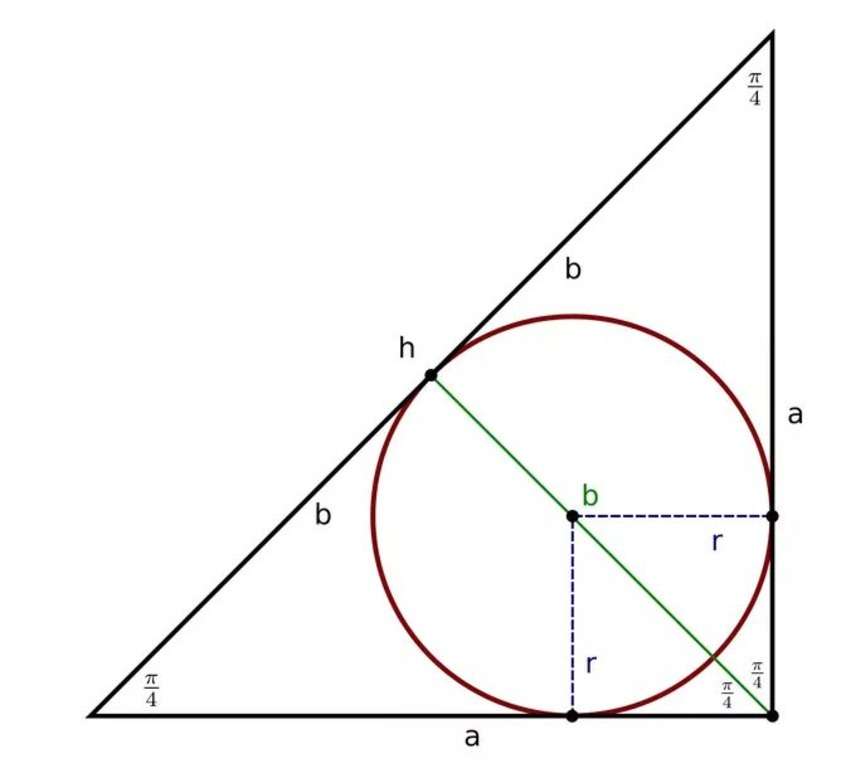
Окружность, вписанная в прямоугольный треугольник

Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.

Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.

Формулировка теоремы о вписанной окружности

В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:

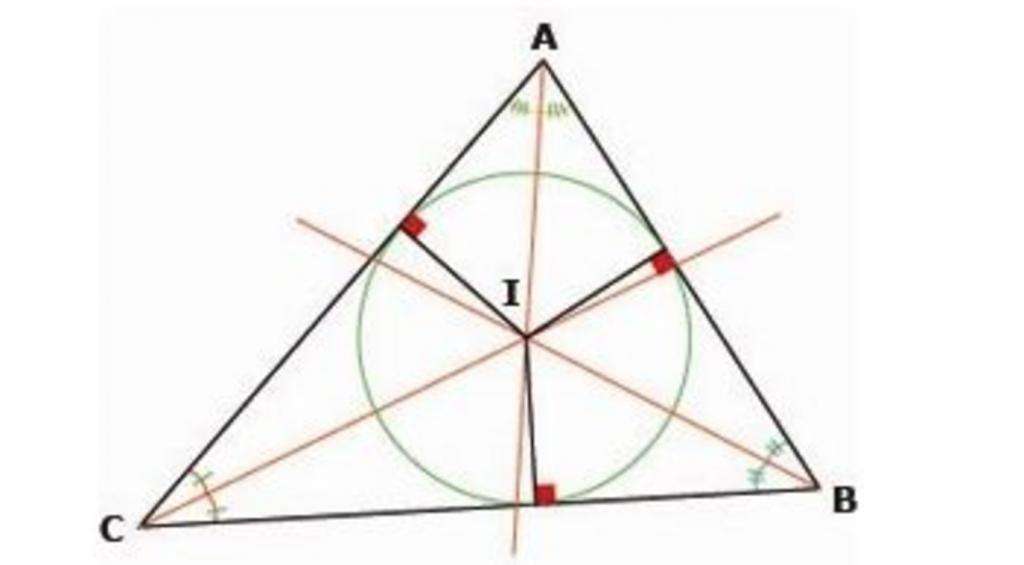
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.

Теорема о центре окружности, вписанной в треугольник

Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.

Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.

Источник

Исследовательская работа на тему «Треугольники. Вписанная окружность»

Тема: Треугольник. Вписанная окружность.

«Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу

геометрии, но и возвысите душу свою»
(Клавдий Птолемей)

«Треугольник является первой фигурой,

которую нельзя разложить на более простые

фигуры…и поэтому считается фундаментом

любой вещи, имеющей границы и форму»

Расширить и углубить знания по теме «Вписанная окружность в треугольниках»

Систематизировать знания по этой теме

Выделить основные свойства, применяемые при решении задач

Привести блок полезных фактов по применению свойств описанного треугольника

Подготовиться к решению задач повышенной сложности в ОГЭ и ЕГЭ

Проверить умение учащихся решать задачи

Основные теоретические сведения

Определение. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника

В этом случае треугольник называют треугольником, описанным около окружности.

Три биссектрисы треугольника пересекаются в одной точке, лежащей строго внутри треугольника. Точка пересечения биссектрис равноудалена от сторон треугольника и является центром вписанной окружности.

Точки касания вписанной окружности сторон треугольника отсекают от его сторон три пары равных между собой отрезков: AK = AM ; BМ = BL; С L = = C К

Вывод. Если окружность вписана в треугольник, то она касается всех его углов, поэтому на основе свойств окружности, вписанной в угол, получаем:

Свойства окружности, вписанной в треугольник

Центр окружности является точкой пересечения биссектрис углов треугольника.

Радиусы, проведенные в точки касания, перпендикулярны к сторонам треугольника.

Равны расстояния от вершины угла до точек касания.

Важно помнить, что в общем случае точка пересечения стороны с биссектрисой треугольника ( D ) и точка касания стороны с вписанной окружностью ( E ) не совпадают. Их совпадение возможно только на основании равнобедренного треугольника. Эти точки полностью совпадают у равностороннего треугольника.

Радиус окружности, вписанной в равнобедренный треугольник

Из пропорции получаем r = .

Аналогично получается формула r = .

Радиус окружности, вписанной в прямоугольный треугольник

Длина гипотенузы ( c ) и полупериметр ( р ) прямоугольного треугольника связаны с радиусом ( r ) вписанной в него окружности следующей простой формулой: r + c = p

Интересны также еще два частных случая для прямоугольного треугольника

Если в условии задачи говорится об описанной около треугольника окружности, то в большинстве случаев строить её не нужно. И наоборот, когда речь идёт о вписанной в треугольник окружности. Здесь не только нужно строить саму окружность, но и проводить радиусы к точкам касания (перпендикуляры к сторонам), а также соединять центр окружности с вершинами треугольника. При этом образуются равные треугольники.

Окружность, вписанная в остроугольный треугольник АВС, касается сторон ВА и ВС в точках Е и F.

а) Докажите что центр окружности, вписанной в треугольник BEF, лежит на окружности, вписанной в треугольник АВС.

б) Найдите расстояние между центрами этих окружностей, если АВ = ВС, BE = 13, EF = 10, S BEF : S ABC = 4:9.

а) Пусть точка O — центр вписанной окружности ΔABC. Тогда O лежит на биссектрисе угла B.

Биссектриса BO пересекает дугу EF в точке M, а отрезок EF в точке K. BE = BF как отрезки касательных, проведённых к окружности из одной точки, отсюда ΔBEF — равнобедренный, значит, биссектриса BK является медианой и высотой. ΔMKE = ΔMKF по двум катетам (EK = KF, MK — общая сторона). Из равенства треугольников следует: EM = MF, а так как равные хорды стягивают равные дуги, то ◡ ME = ◡ MF.

Докажем, что M — центр окружности, вписанной в ΔBEF.

∠ MEF = 1/2 ◡ MF как вписанный, ∠ MEB = 1/2 ◡ ME как угол между касательной BE и хордой ME, а так как ◡ MF = ◡ ME, то ∠ MEF = ∠ MEB, поэтому EM — биссектриса угла BEF. Биссектрисы BK и EM прямоугольника BFE пересекаются в точке M, следовательно, M — центр вписанной окружности.

б) По доказанному в пункте а) центр вписанной окружности ΔBEF — точка M — лежит на вписанной окружности треугольника ABC, следовательно, искомое расстояние равно радиусу вписанной окружности треугольника ABC. В равнобедренном треугольнике BEF BE = BF = 13, EK = KF = 10 : 2 = 5.

В прямоугольном треугольнике BEK по теореме Пифагора

S BEF = 1/2 ∙ EF ∙ BK = 1/2 ∙ P BEF ∙ r, где r — радиус вписанной окружности;

r = (EF ∙ BK) / P ABC = (10 ∙ 12) / (13 + 13 + 10) = 10/3.

ΔBEF ∼ ΔABC по второму признаку подобия ( ∠ B — общий). Из подобия следует: MK/MO = k как радиусы окружностей, вписанных в подобные треугольники. S BEF / S ABC = k 2 = 4/9, k = 2/3.

MO = MK/k = (10 ∙ 3) / (3 ∙ 2) = 5.

Одна из сторон треугольника равна 30 см, а другая делится точкой касания вписанной окружности на отрезки длиной 12 см и 14 см, считая от конца неизвестной стороны. Найти радиус вписанной окружности.

Дано: ∆ ABC,