Как доказать что три точки лежат на одной прямой в плоскости
Как доказать что три точки лежат на одной прямой в плоскости
Если три точки A, B и C лежат на одной прямой, то треугольник ABC обратится в отрезок прямой, а потому его площадь должна быть равна нулю. Полагая в формуле
S = 0, получим условие, при котором три точки лежат на одной прямой
В более удобной форме условие, при котором три точки лежат на одной прямой, можно записать так:
(1)
Подставляя сюда координаты данных точек, получим, что левая часть (1) будет равна
Требование (1) выполнено:
и, значит, три данные точки лежат на одной прямой.
Когда 3 точки лежат на одной прямой
Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.
Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.
Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.
Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.
Решим поставленную задачу
Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:
После преобразования получим:
Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.
Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)
Высшая математика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
Приведённый ознакомительный фрагмент книги Высшая математика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых. Расстояние от точки до прямой
3. Пусть имеются точка М (х1, у1) и некоторая прямая L, представленная уравнением у = ах + с. Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М, описывается уравнением А(х — х1) + В(у — у1) = 0.
Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М:
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М(х1, у1), описывается уравнением А (у — у1) — В(х — х1) = 0.
4. Пусть даны две точки А1 (х1, у1), А2 (х2, у2) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:
1) точки А1, А2 лежат по одну сторону от данной прямой, если выражения (Ах1 + Ву1 + С) и (Ах2 + Ву2 + С) имеют одинаковые знаки;
3) одна или обе точки А1, А2 лежат на данной прямой, если одно или оба выражения соответственно (Ах1 + + Ву1 + С) и (Ах2 + Ву2 + С) принимают нулевое значение.
5. Центральный пучок — это множество прямых, проходящих через одну точку М (х1, у1), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у — у1 = к (х — х1) (параметр пучка к для каждой прямой свой).
Все прямые пучка можно представить уравнением: l(y — y1) = m(x — x1), где l, m — не равные одновременно нулю произвольные числа.
6. Пусть даны точка М (х1, у1) и прямая, заданная уравнением Ах + Ву + С = 0. Расстояние d от этой точки М до прямой:
Отсюда следует: если три точки лежат на одной прямой, то проходящая через них плоскость единственная.
Введение.
В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул. Раздел геометрии, в котором изучаются такие задачи, называется стереометрией (от греческого «стереос»- объемный, пространственный).
План.
I. Основные аксиомы стереометрии————— 4 II. Прямые, плоскости, параллельность———— 6

I.Основные аксиомы стереометрии
· Имеется четыре точки, не лежащие в одной плоскости (рис. 1)
|






· Через любые три точки проходит плоскость.


·
|
Если две плоскости имеют общую точку, то их пересечение есть прямая.
· (рис.2)
Отсюда следует: если три точки лежат на одной прямой, то проходящая через них плоскость единственная.

В качестве следствия выведем прямо из аксиом одно полезное следствие: прямая, имеющая с плоскостью хотя бы две общие точки, целиком лежит в этой плоскости.
|
|
|
|
|
|
|
|
|



Путем несложных доказательств мы находим, что:
· На каждой плоскости выполняются все утвержде-ния планиметрии.
 |
II. Прямые, плоскости, параллельность.
Уже такое основное понятие, как параллельность прямых, нуждается в новом определении:
две прямые в пространстве называются парал-лельнылт, если они лежат в одной плоскости и не имеют общих точек. Так что не попадайтесь в одну из излюбленных экзаменаторами ловушек — не пытайтесь «доказывать», что через две параллельные прямые можно провести плоскость: это верно по определению параллельности прямых! Знаменитую планиметрическую аксиому о единственности параллельной включают и в аксиомы стереометрии, а с её помощью доказывают главное свойство параллельных прямых в пространстве:
· Через точку, не лежащую на прямой, можно провести одну и только одну прямую параллельно данной.
Сохраняется и другое важное свойство параллельных прямых, называемое транзитивностью параллельности:
· Если две прямые а и b параллельны третьей прямой с, то они параллельны друг другу.
Но доказать это свойство в стереометрии сложнее. На плоскости непараллельные прямые обязаны пересекаться и потому не могут быть одновременно параллельны третьей (иначе нарушается аксиома параллельных). В пространстве существуют непараллельные и притом непересекающиеся прямые — если они лежат в разных плоскостях. О таких прямых говорят, что они скрещиваются.
|
|
|
|
|
|















|
|
|
В стереометрии отношение параллельности рассматривается и для плоскостей: две плоскости или прямая и плоскость параллельны, если они не имеют общих точек. Прямую и плоскость удобно считать параллельными и в том случае, когда лежит в плоскости. Для плоскостей и прямых справедливы теоремы о транзитивности:
· Если две плоскости параллельны третьей плоскости, то они параллельны между собой.
· Если прямая и плоскость параллельны некоторой прямой( или плоскости), то они параллельны друг другу.
Наиболее важный частный случай второй теоремы- признак параллельности прямой и плоскости:
· Прямая параллельна плоскости, если она параллельна некоторой прямой в этой плоскости.
А вот признак параллельности плоскостей:
· Если две пересекающиеся прямые в одной плоскости соответственно параллельны двум пересекающимся прямым в другой плоскости, то и плоскости параллельны.
Часто используется и такая простая теорема:
· Прямые, по которым две параллельные плоскости пересекаются третьей, параллельны друг другу.
Посмотрим еще раз на куб (рис. 4). Из признака параллельности прямой и плоскости следует, например, что прямая А¹В¹ параллельна плоскости АВСD (так как она параллельна прямой АВ в этой плоскости), а противоположные грани куба, в частности А¹В¹С¹D¹ и ABCD, параллельны по признаку параллельности плоскостей: прямые A¹B¹ и B¹С¹ в одной грани соответственно параллельны прямым АВ и ВС в другой. И чуть менее простой пример. Плоскость, содержащая параллельные прямые AA¹ и СС¹, пересекают параллельные плоскости АВСD и A¹B¹C¹D¹ по прямым АС и А¹С¹, значит, эти прямые параллельны: аналогично, параллельные прямые В¹С и А¹D. Следовательно, параллельные плоскости АВ¹С и А¹DC, пересекающие куб по треугольникам.
Через три точки можно провести плоскость








Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Существование плоскости, проходящей через три данные точки
Существование плоскости, проходящей через три данные точки
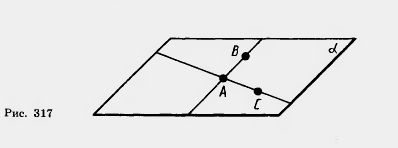
Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Доказательство. Пусть А, В, С — три данные точки, не лежащие на одной прямой (рис. 317). Проведем прямые АВ и АС; они различны, так как точки А, В, С не лежат на одной прямой. По аксиоме Сз через прямые АВ и АС можно провести плоскость 
Докажем, что плоскость а, проходящая через точки А, В, С, единственна. Действительно, плоскость, проходящая через точки А, В, С, по теореме 15.2 содержит прямые АВ и АС. А по аксиоме Сз такая плоскость единственна.
Задача (13). Можно ли провести плоскость через три точки, если они лежат на одной прямой? Объясните ответ.
Решение. Пусть А, В, С — три точки, лежащие на прямой 


Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
сколько плоскостей можно провести через
две различные точки
три различные точки
четыре точки никакие три из которых не лежат на одной прямой.
В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.
Как найти уравнение плоскости, которая проходит через 3 заданные точки
Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:
Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.
Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.
Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.
Из этого мы и будем исходить в дальнейшем.
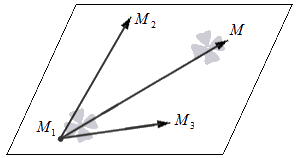
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1
На схеме это будет выглядеть так:
Запишем полученное уравнение в координатной форме:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.
В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.
Примеры задач на составление уравнения плоскости, проходящих через 3 точки
Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.
Решение
Используем поочередно оба способа.
Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →
Это и есть нужное нам уравнение плоскости, которая проходит через три точки.
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73
Мы получили нужное нам уравнение.
А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.
Решение
Векторное произведение будет равно:
M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →
Если мы используем второй способ, у нас получится:
x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0
Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги: