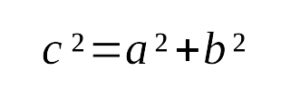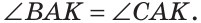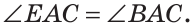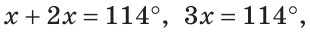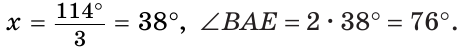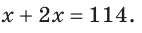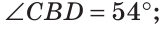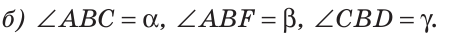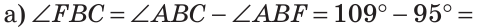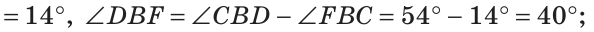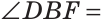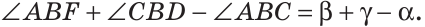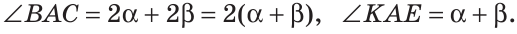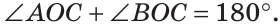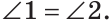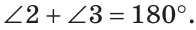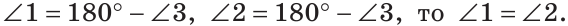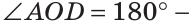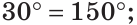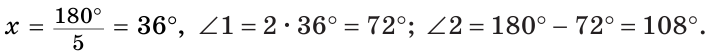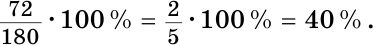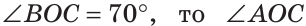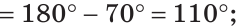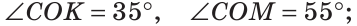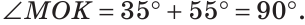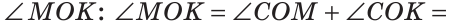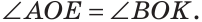Как доказать что угол острый

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

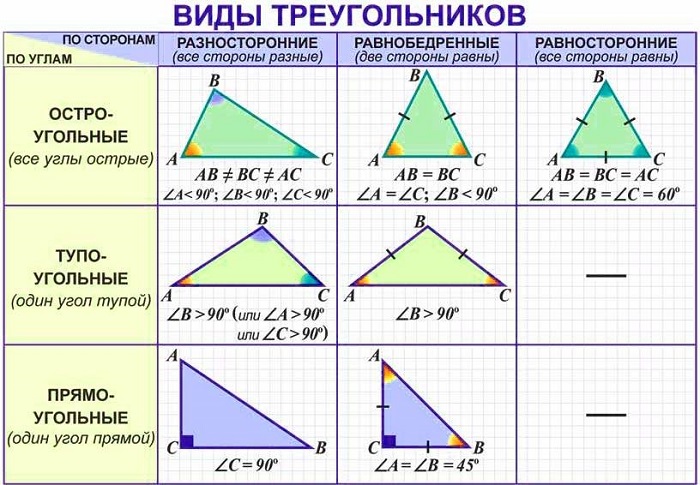
Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

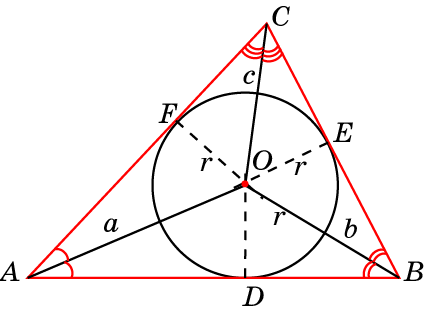
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

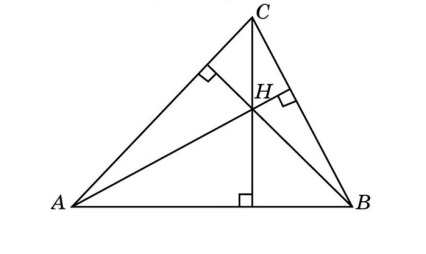
2. Высоты пересекаются в одной точке, образуя ортоцентр.

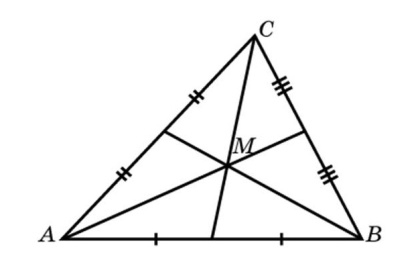
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

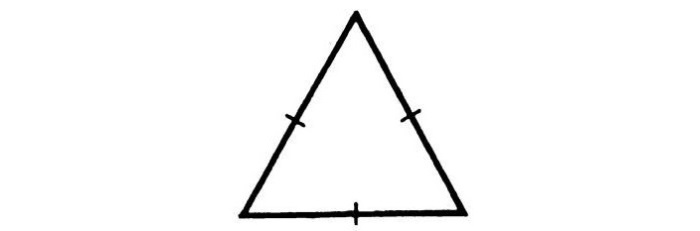
Равносторонний треугольник

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

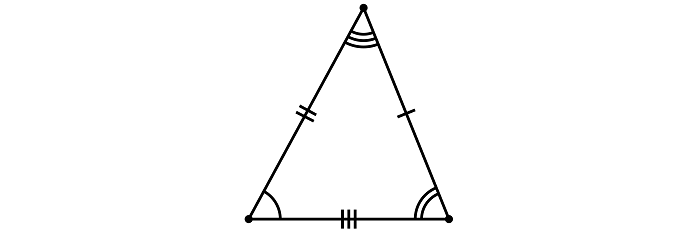
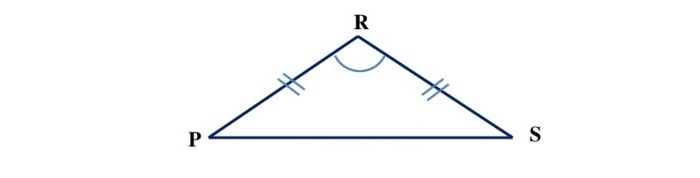
Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

Источник

Прямоугольный треугольник: Признаки Равенства и Подобия

Определение

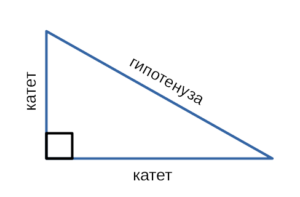
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

Формулы:

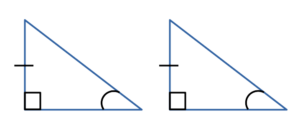
Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Источник

Геометрия

План урока:

Сумма углов треугольника

Рассмотрим произвольный треугольник АВС. Точки А, В и С не лежат на одной прямой, а потому через В можно провести прямую a, параллельную АС. При этом прямые СВ и АВ окажутся секущими для двух параллельных прямых:

Известно, что секущие образуют пары накрест лежащие углы, причем они равны. Отметим на рисунке эти пары и обозначим их как ∠1, ∠2, ∠3 и ∠ 4.

Равные углы (∠1 = ∠2, ∠3 = ∠4) отметим одним цветом. Также обозначим ∠АВС как ∠5:

С одной стороны, углы 2, 4 и 5 вместе образуют развернутый угол, то есть их сумма равна 180°:

В результате мы получили, что сумма углов треугольника АВС в точности равна 180°! В итоге мы можем сформулировать следующую теорему:

Задание. В треуг-ке один угол равен 50°, а второй – 60°. Чему равен третий угол этого треуг-ка?

Решение. Обозначим углы треугольника как ∠1, ∠2 и ∠3.

Получили обыкновенное уравнение с одной переменной. Для его решения просто перенесем слагаемые 50° и 60° из левой части в правую:

Задание. Докажите, что у любого треуг-ка есть хотя бы один угол, который не превосходит 60°.

Решение. Докажем это утверждение методом «от противного». Пусть существует такой треуг-к, у которого каждый из углов больше 60°. Это можно записать в виде трех неравенств:

В итоге имеем, что в сумме эти углы больше 180°, а это невозможно. Это противоречие, следовательно, треуг-к с тремя углами, каждый из которых больше 60°, не существует.

Задание. Основанием рав-бедр. ∆АВС является сторона АС. Известно, что ∠В = 40°. Чему равны ∠А и ∠С этого треуг-ка?

Решение. Сначала необходимо вспомнить важное свойство – углы равнобедренного треугольника при его основании равны друг другу. В нашем случае это значит, что ∠А = ∠С:

Задание. Один из углов при основании рав-бедр. треуг-ка равен 50°. Найдите два других угла.

Решение. Построим рисунок по условию задачи:

Отдельного внимания заслуживает равносторонний треуг-к. Напомним, что у него равны все три стороны. Построим его:

Теперь подумаем о том, чему равны его углы. С одной стороны, мы можем рассматривать ∆АВС как рав-бедр. с основанием АС, ведь AB = BC. Тогда∠А = ∠С. Но с другой стороны, всё тот же ∆АВС мы можем одновременно считать и рав-бедр. с основанием АВ, ведь АС = ВС. Из этого следует, что ∠А = ∠С. В итоге получаем, что все три угла ∆АВС равны:

Итак, получили удивительный факт – в равностороннем треуг-ке все углы равны 60°!

Рассмотрим чуть более сложную задачу, где неизвестен ни один из углов треуг-ка, однако известны некоторые соотношения между ними.

Задание. Первый угол треуг-ка больше второго в 2 раза, а третий равен сумме первых двух углов. Чему равны углы треуг-ка?

Решение. Для большей наглядности примем первый угол треуг-ка за неизвестную величину, то есть за х. Тогда второй угол будет равен 2х, а третий окажется равным их сумме:

Внешние углы треугольника

Построим некоторый треуг-к, а потом продлим одну из его сторон. На рисунке мы продлили сторону АС. В результате образуется угол, который называют внешним углом треугольника:

На рисунке видно, что ∠ВСD является внешним. Но одновременно можно утверждать и ещё один факт – углы ∠АСВ и ∠ВСD являются смежными. Это позволяет нам дать следующее определение:

В итоге мы доказали, что внешний угол треугольника равен сумме двух углов треуг-ка, которые с ним не смежны.

Задание. У ∆АВС ∠А = 50°, ∠В = 75°. Найдите величину внешнего угла, смежного с ∠С.

Решение. В данном случае, согласно доказанному нами правилу, достаточно просто сложить ∠А и ∠B:

Рассмотрим ещё несколько более тяжелых задач.

Задание. В ∆АВС проведены биссектрисы угловА и B. Они пересекаются в точке М. Известно, что ∠А = 58°, ∠B = 96°. Найдите ∠АМB.

Решение. Устно такую задачу не решить, поэтому построим рисунок:

АМ – это биссектриса, а она разбивает∠ВАС на два равных угла. Поэтому мы можем вычислить ∠ВАМ:

Отметим найденные углы на рисунке:

Обратите внимание на ∆АВМ, который выделен красным цветом. Теперь мы знаем два угла в нем. Значит, можно найти и третий! Запишем для ∆АВМ сумму его углов:

Задание. Построен внешний угол равнобедренного треугольника, который смежен с вершиной, лежащей против основания. Далее построили биссектрису этого внешнего угла. Докажите, что эта биссектриса будет параллельна основанию.

Решение. Выполним построение:

Пусть АС – это основание рав-бедр. ∆АВС. Тогда внешний угол должен быть проведен к вершине В, ведь именно она лежит против основания. Обозначим внешний угол как ∠СВD (для этого мы просто добавили точку Dна продолжение отрезка АВ). Далее проводим биссектрису ВК. Нам требуется доказать, что ВК||АС.

Поступим очень просто – обозначим неизвестную нам величину угла при основании как х. То есть

В результате мы получили, что и ∠С, и ∠CBK равны х, то есть они равны и друг другу. Однако эти углы являются накрест лежащими для прямых АС и ВК и секущей ВС. Из равенства накрест лежащих углов следует, что АС||ВК.

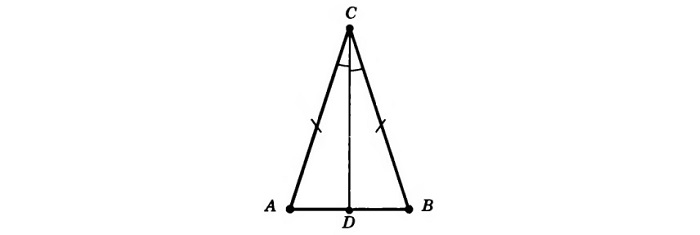
Задание. В ∆АВС проведена медиана АМ, причем ее длина равна ВМ. Найдите ∠А.

Решение. Напомним, что медиана – это прямая, разбивающая сторону на два равных отрезка. То есть ВМ = МС. По условию АМ = ВМ, значит, имеет место двойное равенство:

Посмотрите на рисунок – здесь есть сразу два рав-бедр. треуг-ка! Это ∆АВМ (с основанием АВ) и ∆АМС (с основанием АМС). Обозначим∠В как х, а ∠С – как у. Углы при основании рав-бедр. треуг-ков одинаковы, а потому

Сравнение сторон и углов треугольника

Докажем следующую теорему:

Построим ∆АВС, в котором сторона АВ будет длиннее, чем АС. Нам надо доказать, что ∠С >∠B:

Выполним дополнительное построение – отметим на прямой АВ такую точку D, что AD = АС. Точка D будет располагаться на отрезке АВ, ведь АВ больше АС, а, значит, и больше АD. Также соединим C и D отрезком:

Теперь рассмотрим ∆ADC. Он является рав-бедр., ведь AD = AC. Из этого следует, что ∠ADC = ∠ACD.

Можно заметить, что ∠АDС является внешним углом для ∆BDC. Это значит, что

Мы доказали только первую часть теоремы. Теперь надо доказать обратное утверждение – против большего угла находится большая сторона треугольника. Предположим обратное, что существует ∆АВС, в котором ∠С>∠B, но не выполняется условие АВ >AC. Тогда либо АВ = ВС, либо АВ AC.

Задание. В ∆АВС известны углы:

Запишите стороны этого треуг-ка в порядке возрастания.

Решение. Всё очень просто – чем больше сторона, тем против большего угла она лежит. Поэтому самая большая сторона – это АВ, вторая по длине – АС, а наименьшая сторона – ВС. То есть BС

Доказанная теорема помогает сформулировать важный признак рав-бедр. треуг-ка:

Действительно, против равных углов должны лежать равные стороны, в противном случае сложится ситуация, когда в треуг-ке против сторон разной длины будут лежать равные углы, что невозможно.

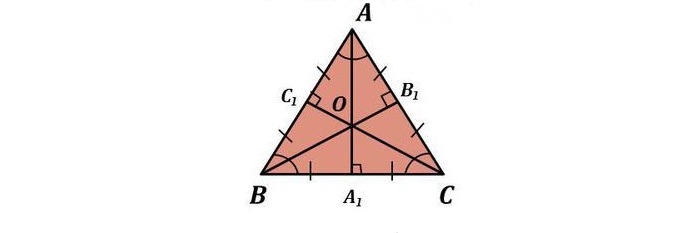
Задание. В рав-бедр. ∆АВС основанием является АС. Из точек А и С проведены биссектрисы, которые пересеклись в точке О. Докажите, что ∆АОС также является рав-бедр.

Ясно, что ∠ВАС = ∠ВСА, так как это углы при основании рав-бедр. ∆АВС. С другой стороны, ∠ОАС равен половине ∠ВАС, ведь АО – биссектриса:

В итоге имеем, что ∠ОАС и ∠АСО равны. Но тогда в ∆АОС есть два одинаковых угла, а потому он является рав-бедр. (АО = ОС).

Неравенство треугольника

Следующая важная теорема называется неравенством треугольника:

Попробуем доказать неравенство треугольника. Возьмем произвольный ∆АВС и покажем, что сторона АВ меньше, чем величина ВС + АС. Для этого «дорисуем» к отрезку АС ещё один отрезок СD, равный BC, при этом АС и СD должны лежать на одной прямой:

Так как AD = АС + СD, то нам достаточно показать, что АВ

Получается, что в ∆АВD сторона АВ лежит против меньшего угла по сравнению со стороной АD. Значит, эта сторона должна быть меньше АD, что мы и пытаемся доказать.

Доказанная теорема означает, что не всякий треуг-к можно построить по его сторонам. Так, у нас никогда не получится построить треуг-к, у которого стороны равны 2, 3 и 7 см, так как одна из этих длин больше, чем сумма двух других:

Верно обратное утверждение – если все заданные длины удовлетворяют неравенству, то треуг-к построить можно.

Задание. Известны две стороны равнобедренного треугольника, они равны 25 и 10 см. Какая из них является основанием?

Решение. Рассмотрим сперва случай, когда основание равно 25 см. Тогда две другие стороны имеют длину 10 см. Их сумма (10 см + 10 см = 20 см) меньше основания. Такая ситуация невозможно из-за неравенства треуг-ка.

Ситуация же, при которой основание имеет длину 10 см, вполне допустима. Тогда две другие стороны равны 25 см, и для каждой стороны неравенство треуг-ка выполняется:

Источник

Содержание:

Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.

Два угла называются равными, если их можно совместить наложением.

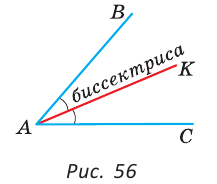
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.

Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.

На рисунке 56 луч АК — биссектриса угла ВАС и

На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.

Углы измеряются в градусах, минутах, секундах.

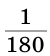
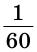
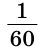
Развернутый угол равен 180°; часть развернутого угла называется градусом и обозначается 1°; часть одного градуса называется минутой и обозначается 1′; часть минуты называется секундой и обозначается 1″.

Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».

Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».

Определения

Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.

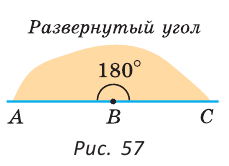
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).

На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.

Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.

Аксиомы

Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.

Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.

Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.

Пример №1

Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.

Решение:

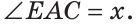
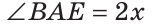
Пусть Тогда (рис. 61).

По аксиоме измерения углов

Тогда

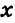
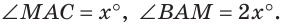
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой пишут знак градуса: Тогда в уравнении знак градуса писать не нужно:

2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.

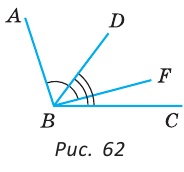
Пример №2

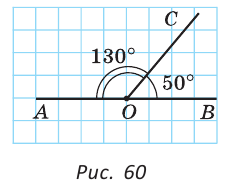
Внутри угла проведены лучи BD и BF (рис. 62).

Найти величину угла DBF, если:

Решение:

Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.

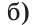
Отсюда

Ответ:

Пример №3

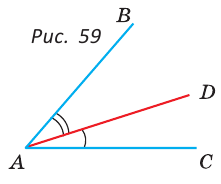
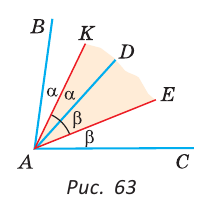
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).

Доказательство:

Так как АК иАЕ — биссектрисы, то 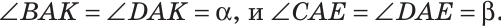Тогда

Следовательно, 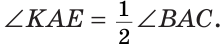Что и требовалось доказать.

Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».

Геометрия 3D

В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.

Геометрия 3D

В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 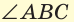— линейный угол изображенного двугранного угла.

Смежные углы. Вертикальные углы

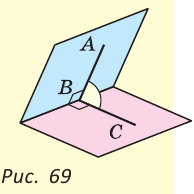
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.

Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.

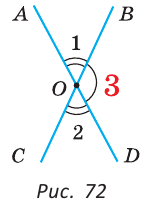
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.

Дано: 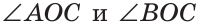— смежные.

Доказать:

Доказательство:

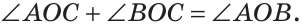
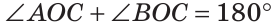
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов Поэтому . Теорема доказана.

Следствия.

Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.

Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.

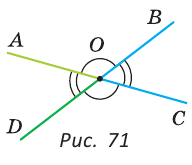
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.

Теорема (свойство вертикальных углов). Вертикальные углы равны.

Дано: 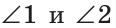— вертикальные (рис. 72).

Доказать:

Доказательство:

Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов 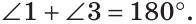Углы 2 и 3 также смежные,

Так как

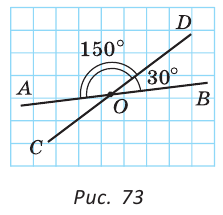
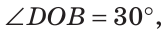
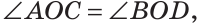
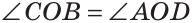
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73) то как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.

При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.

Угол между параллельными прямыми считается равным 0°.

Пример №4

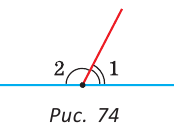
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.

Решение:

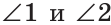
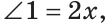
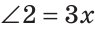
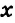
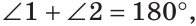
а) Пусть — данные смежные углы (рис. 74). Согласно условию (градусную меру одной части принимаем за ). По свойству смежных углов

то есть

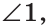
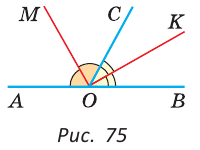
б) Меньшим является а 72° от 180° составляют

Пример №5

а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если 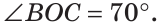б) Доказать, что биссектрисы смежных углов образуют прямой угол.

Решение:

а) Если

б) Так как ОМ и ОК — биссектрисы, то

Найдем градусную меру По свойству смежных углов Тогда . Что и требовалось доказать.

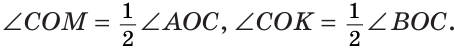
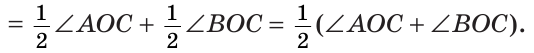
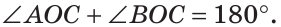
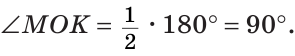
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.

Пример №6

Доказать, что биссектрисы вертикальных углов образуют развернутый угол.

Решение:

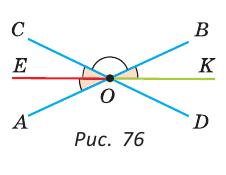
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что — развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому

б) так как лучи OA и ОВ дополнительные, и поэтому — развернутый. Заменив в последнем равенстве на равный ему получим Отсюда следует, что — развернутый.

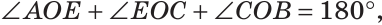
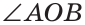
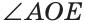
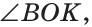
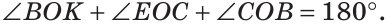
Замечание. Из решения задачи следует свойство: если 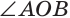— развернутый и — вертикальные.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник