Как доказать что угол равен другому углу
Как доказать, что углы треугольников равны
Как доказать, что углы треугольников равны? Рассмотрим возможные варианты.
Углы треугольников могут быть равны в следующих случаях:
1) Угол — общий (один и тот же угол принадлежит одновременно двум различным треугольникам).
3) Углы при основании равнобедренного треугольника равны.
4) Если дана биссектриса треугольника, то исходный угол разделен ею на два равных угла.
5) Если дана высота треугольника, то она образует два прямых (а значит, равных) угла.
6) Угол, смежный с прямым, есть прямой угол (а значит, они равны между собой).
7) Углы, смежные с равными, равны между собой.
8) Соответствующие углы равных треугольников равны между собой.
9) Если к равным углам прибавить равные углы, то получим равные углы.
10) Если из равных углов вычесть равные углы, то получим равные углы.
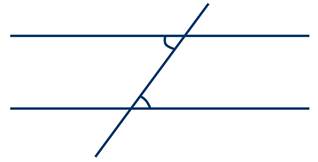
11) Внутренние накрест лежащие углы при параллельных прямых и секущей равны между собой.
12) Соответственные углы при параллельных прямых и секущей равны между собой.
13) Углы равны по условию.
14) Углы равны по построению.
15) Углы равны по доказанному.
5 Comments
На вопрос вы так и не ответили. «Как доказать, что углы равны?» а не «В каких случаях углы равны?». Как-то так; информация не полная, а так все отлично.
Равенство углов следует из равенства треугольников. Значит, в большинстве задач, чтобы доказать, что углы равны, нужно доказать равенство треугольников.
Еще можно доказать, что два угла являются углами при основании равнобедренного треугольника, соответственными или внутренними накрест лежащими углами при параллельных прямых и т.д. — об этом сказано выше.
А если в «моём» случае не подходит?
Значит, искать «свой», подходящий вариант.
Спасибо, очень много вариантов! Я уж думала никогда не найду ответ, а тут белая куча ответов! Спасибо!
Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов
Урок 18. Геометрия 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов»
Вспомним теорему о равенстве накрест лежащих углов:
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
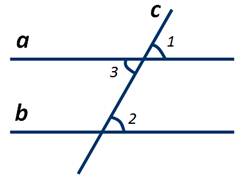
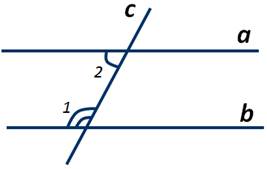
Пусть параллельные прямые а и b пересечены секущей c. Необходимо доказать, что соответственные углы 1 и 2 равны. Так как прямая а параллельна прямой b, то накрест лежащие углы 2 и 3 равны. ∠1 и ∠3 равны как вертикальные. Из равенств ∠2=∠3 и ∠1=∠3 следует, что ∠1=∠2. Теорема доказана.
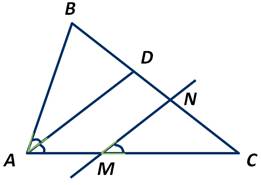
Пусть прямая MN параллельная биссектрисе AD треугольника АВС.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.
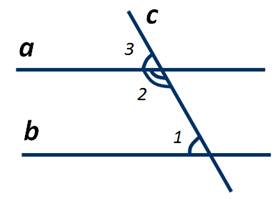
Пусть параллельные прямые а и b пересечены секущей c. Доказать, ∠1+∠2=180 градусов. Так как прямая а параллельна прямой b, то соответственные ∠1 и ∠3 равны. ∠2+∠3=180 градусов, так как углы 2 и 3 смежные. Тогда, из равенств угол ∠1=∠3 и ∠2+∠3=180 градусов, следует, что ∠1+∠2=180 градусов. Теорема доказана.
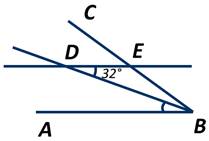
Например: пусть прямая DE параллельна стороне АВ треугольника АВС. Тогда ∠BAD+∠ADE=180 градусов.
Углы АВС и CED являются соответственными углами при параллельных прямых АВ и DE и секущей ВС, а значит, они равны. Следовательно, ∠CED=64 градуса.
Градусная мера одного из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, меньше градусной меры другого на 26 градусов. Вычислить градусные меры этих углов.
Пусть ∠1=x, тогда ∠2=x-26. Так как ∠1 и ∠2 являются внутренними односторонними при параллельных прямых а и b и секущей с, то их сумма равна 180 градусов, то есть ∠1+∠2=180 градусов.
Как доказать равенство треуголников? Примеры!
Первый признак равенства треугольников
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство. Пусть в треугольниках АВС и А 1 В 1 С 1 имеют место равенства
AB= A1B1,
ÐBAC = ÐB1A1C1,
ÐАВС= ÐА1В1С1.
Поступим так же, как и в предыдущем случае. Наложим треугольник А1В1С1 на треугольник АВС так, чтобы совпали стороны AB и A1B1 и прилегающие к ним углы. Как и в предыдущем случае, при необходимости треугольник А1В1С1 можно «перевернуть обратной стороной».
Тогда треугольники совпадут полностью. Значит, они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Пусть для треугольников ABC и A1B1C1
имеют место равенства АВ = А1В1,
ВС = В1С1,
СА = С1А1.
Перенесем треугольник А1В1С1 так, чтобы сторона А1В1 совпала со стороной АВ, при этом должны совпасть вершины A1 и A, B1 и B.
Рассмотрим две окружности с центрами в A и B и радиусами соответственно AC и BC.
Эти окружности пересекаются в двух симметричных относительно AB точках: C и C2. Значит, точка C1 после переноса указанным образом треугольника A1B1C1 должна совпасть либо с точкой C, либо с точкой C2.
В обоих случаях это будет означать равенство треугольников ABC и A1B1C1, поскольку треугольники ABC и ABC2 равны (эти треугольники симметричны относительно прямой AB.)
Геометрия, Признаки равенства треугольников
Рис. 1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Признаки равенства треугольников, геометрия ЕГЭ и ГИА
Рис. 2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис. 2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Признаки равенства треугольников, ГИА, ЕГЭ
Рис. 3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Геометрия, Признаки равенства треугольников
Рис. 1
Два треугольника называются равными, если их можно совместить наложением. На рисунке 1 изображены равные треугольники ABC и А1В1С1. Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т. е. попарно совместятся их вершины и стороны. Ясно, что при этом совместятся попарно и углы этих треугольников.
Таким образом, если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Отметим, что в равных треугольниках против соответственно равных сторон (т. е. совмещающихся при наложении) лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.
Так, например, в равных треугольниках ABC и A1B1C1, изображенных на рисунке 1, против соответственно равных сторон АВ и А1В1 лежат равные углы С и С1. Равенство треугольников ABC и А1В1С1 будем обозначать так: Δ ABC = Δ А1В1С1. Оказывается, что равенство двух треугольников можно установить, сравнивая некоторые их элементы.
Признаки равенства треугольников, геометрия ЕГЭ и ГИА
Рис. 2
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны (рис. 2).
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1 (см. рис. 2). Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Аналогично методом наложения доказывается теорема 2.
Признаки равенства треугольников, ГИА, ЕГЭ
Рис. 3
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (рис. 34).
Замечание. На основе теоремы 2 устанавливается теорема 3.
Теорема 3. Сумма любых двух внутренних углов треугольника меньше 180°.
Из последней теоремы вытекает теорема 4.
Теорема 4. Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Признаки равенства треугольников:
1)По 2 сторонам и углу между ними
Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого
треугольника то такие треугольники равны.
2)По стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам
другого треугольника то такие треугольники равны.
3)По трём сторонам
Если три стороны одного треугольника соответственно равны
трём сторонам другого треугольника то такие треугольники равны.
Как доказать, что треугольники равны
Как доказать, что треугольники равны? Для этого надо знать признаки равенства треугольников и уметь определять в треугольниках равные стороны и равные углы.
Очень удобный и эффективный инструмент, облегчающий доказательство равенства треугольников, — визуализация задачи. Выделение треугольников разными цветами помогает лучше понять условие и может подсказать ход решения. Если у треугольников есть общий угол либо общая сторона, цветовая визуализация позволяет сразу же увидеть это.
Рекомендую завести специальную тетрадь для записи теоретического материала.
На отдельных страницах запишите:
План доказательства равенства треугольников.
1) Определяем, какие именно треугольники равны (название треугольников).
2) Выделяем треугольники, равенство которых надо доказать, разными цветами.
3) Отмечаем на чертеже стороны и углы, равенство которых дано по условию.
4) Проверяем, есть ли у данных треугольников общая сторона либо общий угол.
5) Анализируем, что имеем с точки зрения признаков равенства треугольников. Например, если у треугольников уже есть две пары равных сторон, то нужно доказывать либо равенство углов между этими сторонами, либо равенство третьей пары сторон.
6) Если треугольники имеют прямой угол, используем признаки равенства прямоугольных треугольников.
7) Ищем недостающие пары равных углов или равных сторон ( при необходимости используем подсказки).
8) Если данных недостаточно, выясняем, можно ли доказать равенство других треугольников, чтобы из него получить равенство сторон или (и) равенство углов для наших треугольников.
9) Если необходимо, проводим дополнительные построения.
На следующем этапе на конкретных задачах рассмотрим, как доказывать, что треугольники равны.
5 Comments
Большое спасибо:) информация очень полезная)) теперь хоть умею доказывать равенство треугольников
Эля, я рада, что эта информация помогла Вам разобраться в данной теме. Желаю дальнейших успехов в изучении геометрии!
Спасибо огромное очень помогло наконец научился доказывать равенства треугольников!
Спасибо вам большое) наверно из всех сайтов про геометрию выбираю только ваш.Очень подробно и хорошо объясняетте. ещё спасибо за то что ваш сайт и вы помогли мне подняться с оценками по данному предмету. СПАСИБО!
Alex, желаю Вам дальнейших успехов в освоении геометрии!
Теоремы за 7 класс по геометрии
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
Прежде чем перейти к доказательству теоремы необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.
Что такое треугольник и когда они считаются равными?
Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами ).
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными ). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Два треугольника: ABC и DEF (рисунок 2).
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠ АСВ = ∠ EFD).
Поскольку имеется равенство углов ( ∠ АСВ = ∠ EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
MN = PR ∡ N = ∡ R ∡ M = ∡ P
Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
4. Совмещены все вершины треугольников, то есть Δ MNK и Δ PRT полностью совместятся, значит они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
MN = PRKN = TRMK = PT
Опять попробуем совместить треугольники Δ MNK и Δ PRT наложением и убедится, что соответственно равные стороны гарантирует и равенство соответственных углов этих треугольников и они полностью совпадут.
Доказательство. Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.
Докажем единственность перпендикуляра АВ. Допустим,
существует другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это, как мы знаем, невозможно. Теорема доказана.
Медианы, биссектрисы и высоты треугольника
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Поэтому для построения медианы необходимо выполнить следующие действия:
1. Найти середину стороны;
2. Соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.
У треугольника три стороны, следовательно, можно построить три медианы.
Все медианы пересекаются в одной точке.
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Поэтому, для построения биссектрисы необходимо выполнить следующие действия:
1. Построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части );
2. Найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3. Соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.
У треугольника три угла и три биссектрисы.
Все биссектрисы пересекаются в одной точке.
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
Поэтому, для построения высоты необходимо выполнить следующие действия:
1. Провести прямую, содержащую одну из сторон треугольника ( в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике );
2. Из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней ( перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90° ) — это и будет высота.
Также как медианы и биссектрисы, треугольник имеет три высоты.
Высоты треугольника пересекаются в одной точке.
Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличается.
Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.
Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.
Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самим коротким отрезком.
Если у треугольника две стороны равны, то такой треугольник называют равнобедренным .
Если у треугольника все три стороны равны, то такой треугольник является равносторонним.
Равнобедренный треугольник имеет некоторые свойства, которые не имеют треугольники с разными сторонами.
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
4. В равнобедренном треугольнике высота, проведённая к основанию, является биссектрисой и медианой.
У равных треугольников равны все соответствующие элементы:
1. ∡ A = ∡ C — доказано, что прилежащие основанию углы равны.
2. AD = DC — доказано, что биссектриса является медианой.
Можно очень легко самостоятельно доказать и третье и четвёртое свойство.
1. Первый признак параллельности.
Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.
Пусть прямые АВ и СD пересечены прямой ЕF и / 1 = / 2. Возьмём точку О — середину отрезка КL секущей ЕF (черт. 189).
Опустим из точки О перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD, АВ_|_МN. Докажем, что и СD_|_МN.
Для этого рассмотрим два треугольника: МОЕ и NОК. Эти треугольники равны между собой. В самом деле: / 1 = / 2 по условию теоремы; ОK = ОL — по построению;
/ МОL = / NОК, как вертикальные углы. Таким образом, сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника; следовательно, /\ МОL = /\ NОК, а отсюда и
/ LМО = / КNО, но / LМО прямой, значит, и / КNО тоже прямой. Таким образом, прямые АВ и СD перпендикулярны к одной и той же прямой МN, следовательно, они параллельны (§ 33), что и требовалось доказать.
Примечание. Пересечение прямых МО и СD может быть установлено путём поворота треугольника МОL вокруг точки О на 180°.
2. Второй признак параллельности.
Посмотрим, будут ли параллельны прямые АВ и СD, если при пересечении их третьей прямой ЕF равны соответственные углы.
Пусть какие-нибудь соответственные углы равны, например / 3 = / 2 (черт. 190);
/ 3 = / 1, как углы вертикальные; значит, / 2 будет равен / 1. Но углы 2 и 1 — внутренние накрест лежащие углы, а мы уже знаем, что если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны. Следовательно, АВ || СD.
Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые параллельны.
На этом свойстве основано построение параллельных прямых при помощи линейки и чертёжного треугольника. Выполняется это следующим образом.
Приложим треугольник к линейке так, как это показано на чертеже 191. Будем передвигать треугольник так, чтобы одна его сторона скользила по линейке, а по какой-либо другой стороне треугольника проведём несколько прямых. Эти прямые будут параллельны.
3. Третий признак параллельности.
Пусть нам известно, что при пересечении двух прямых АВ и СD третьей прямой сумма каких-нибудь внутренних односторонних углов равна 2 d (или 180°). Будут ли в этом случае прямые АВ и СD параллельны (черт. 192).
Отсюда / 1 = / 3, а эти углы внутренние накрест лежащие. Следовательно, АВ || СD.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 2 d, то эти две прямые параллельны.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти две прямые параллельны.
Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.
Аксиома параллельных прямых.
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Иногда эту аксиому называют как одно из свойств параллельных прямых, но на справедливости этой аксиомы строятся многие доказательства в геометрии.
Другие свойства параллельных прямых.
1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.
2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Эти свойства в отличии от аксиомы нужно доказать.
Докажем 1. Свойство.
Используем противоположное суждение.
Попробуй доказать самостоятельно 2. Свойство.
Таким же методом от противоположного суждения попробуй представить, что возможно ситуация, когда прямая пересекает одну из параллельных прямых, но не пересекает другую.
Свойства углов, которые образуются при пересечении двух параллельных прямых с третьей секущей мы уже назвали в первой части теории.
При пересечении двух параллельных прямых третьей секущей:
— накрест лежащие углы равны,
— соответственные углы равны,
Теорема об углах, образованных двумя параллельными прямыми и секущей
Теорема об углах, образованных двумя параллельными прямыми и секущей
Теоремы
Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Если при пересечении двух прямых секущей накрест лежащие углы равны, топрямые параллельны.
Доказательство
3.4. Углы с соответственно параллельными и перпендикулярными сторонами
1. Сумма углов треугольника
Теория:
Следствия из теоремы о сумме углов треугольника
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Остроугольный, прямоугольный и тупоугольный треугольники
Как гласит четвёртое следствие из теоремы о сумме углов треугольника, можно выделить три вида треугольников в зависимости от углов.
У треугольника KLM все углы острые.
На рисунке MN — гипотенуза, MK и KN — катеты.
У треугольника KLM один угол тупой.
Соотношения между сторонами и углами треугольника. Неравенство треугольника
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство. Пусть в треугольнике ABC сторона АВ больше стороны АС (рис.1, а).
Докажем, что ∠ С > ∠ В. Отложим на стороне АВ отрезок AD, равный стороне АС (рис.1, б). Так как AD ∠ C > ∠ 1. Угол 2 — внешний угол треугольника BDC, поэтому Z 2 > Z В. Углы 1 и 2 равны как углы при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В.
Справедлива и обратная теорема (ее доказательство проводится методом от противного).
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Из теоремы 1 вытекает
Следствие 1. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
Доказательство следствия проводится методом от противного.
Из следствия 1 следует, что если три угла треугольника равны, то треугольник равносторонний.
Из теоремы 2 получаем
Следствие 3. В прямоугольном треугольнике гипотенуза больше катета.
С использованием теоремы 2 устанавливается следующая теорема.
Теорема 3. Каждая сторона треугольника меньше суммы двух других сторон.
Следствие 4. Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства:
АВ
Каждое из этих неравенств называется неравенством треугольника.
1. Прямоугольные треугольники
Теория:
Свойства прямоугольного треугольника
Справедливо и обратное суждение.
Признаки равенства прямоугольных треугольников
В прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны. Поэтому согласно теоремам о первом и втором признаках равенства треугольников справедливы следующие утверждения:
если катеты одного прямоугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны (рис. 101);
если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 102).
Учитывая, что сумма двух острых углов прямоугольного треугольника равна 90°, получаем еще два признака равенства прямоугольных треугольников:
если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны (рис. 103);
если катет и противолежащий ему угол одного прямоугольного треугольника соответственно равны катету и противолежащему углу другого прямоугольного треугольника, то такие треугольники равны (рис. 104).
В самом деле, в таких треугольниках два других острых угла также равны, поэтому указанные треугольники равны по второму признаку равенства треугольников.
Рассмотрим еще один признак равенства прямоугольных треугольников.
Теорема. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Расстояние между двумя параллельными прямыми – определение.
Расстояние между двумя параллельными прямыми – это расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Приведенное определение расстояния между двумя параллельными прямыми справедливо как для параллельных прямых на плоскости, так и для прямых в трехмерном пространстве. Более того, такое определение расстояния между двумя параллельными прямыми принято не случайно. Оно тесно связано со следующей теоремой.
Все точки одной из двух параллельных прямых удалены на одинаковое расстояние от другой прямой.