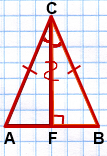
Как доказать что высота это биссектриса
Если биссектриса треугольника является его высотой
Какой вывод следует из того, что биссектриса треугольника является его высотой?
Если в треугольнике биссектриса является также его высотой, то такой треугольник — равнобедренный.

CD — биссектриса и высота.
Проведем анализ задачи.
Какой треугольник — равнобедренный? Треугольник, у которого две стороны равны. Значит, нам нужно доказать, что две стороны ∆ ABC равны: AC=BC.
Равенство сторон вытекает из равенства треугольников. Следовательно, задача сводится к доказательству равенства двух треугольников.
Докажем, что ∆ADC и ∆ BDC равны.
Что нам известно об этих треугольниках?
Поскольку CD — биссектриса ∆ ABC, то она делит угол ACB на два равных угла. Значит, углы ACD и BCD равны.
Так как CD — высота ∆ ABC, то она образует со стороной AB два прямых угла.
Таким образом, у треугольников ADC и BDC уже есть две пары равных углов.

Этот прием дает возможность увидеть подсказку, что сторона CD — общая.
Три пары равных элементов для доказательства равенства треугольников есть.
Переходим непосредственно к доказательству.
Рассмотрим ∆ ADC и ∆ BDC.
1) ∠ACD=∠BCD (так как CD — биссектриса треугольника ABC по условию).
2) ∠ADC=∠BDC=90º (так как CD — высота треугольника ABC по условию).
3) Сторона CD — общая.
Следовательно, ∆ ADC = ∆ BDC (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AC=BC. Значит, ∆ ABC — равнобедренный с основанием AB (по определению равнобедренного треугольника).
Что и требовалось доказать.
Если в треугольнике совпадают биссектрисы и высоты, проведенные к каждой из сторон, то такой треугольник — равносторонний (по доказанному выше, у него каждый две стороны равны между собой, а значит, все три стороны равны).
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
Доказательство
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
Высота равнобедренного треугольника, проведенная к основанию
Теорема (свойство высоты равнобедренного треугольника)
Высота равнобедренного треугольника, проведенная к основанию, является его медианой и биссектрисой.
(как боковые стороны равнобедренного треугольника))
2) сторона CF — общая
∠ AFC= ∠ BFC=90º (как смежные)
Сумма углов треугольника равна 180º.
Если из 180º вычесть сумму равных углов, то получим равные углы:
2) ∆ ACF=∆ BCF ( по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AF=BF.
Поэтому CF является также медианой треугольника ABC.
Что и требовалось доказать.
One Comment
Ну вобщем доказательство этой теоремы не совсем корректно. Потому что предполагает предварительное введение признаков равенства треугольников, включая признаки равенства прямоугольных треугольников. Потому что тут напрямую можно воспользоваться равенством тр. AFC и тр. FCB по общему катету CF и гипотенузам AC и BC… Но дело в том, что введение этих признаков требует доказательства ряда теорем и свойств и по курсу геометрии предполагается после этой теоремы. Поэтому по логике такое доказательство не совсем уместно… Мы приходим к логическому противоречию. И потому требуется другое доказательство, не требующее использования признаков равенства треугольников. Это же доказательство ещё хуже, поскольку тут потребовали ещё и равенства углов противолежащих равным сторонам. (Это отдельная теорема, которая так же излагается после). Хотя этот недостаток легко устраняется… Но доказательство получается довольно таки запутанным. Вначале надо провести биссектрису(как обычно и доказывается эта теорема) и доказать равенство этих углов. Но если выбрать такой путь, то гораздо проще провести сразу биссектрису(не высоту. ) и доказать всю теорему. А потом ввести следствия и доказать эту на основании уже доказанной скажем методом от противного. Так обычно и излагается этот материал. Но если мы хотим доказать все свойства через высоту, то надо придумать что-то другое…
Биссектриса угла
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.
Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…
Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!
Биссектриса угла — коротко о главном
Биссектриса угла — это линия, делящая угол пополам.
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.
Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.
Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.
А теперь подробнее…
Определение биссектрисы угла
Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?
Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):
Биссектриса угла – это линия, делящая угол пополам.
Или еще вот такое определение биссектрисы:
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
А вот определение биссектрисы треугольника:
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
Биссектриса равнобедренного треугольника
Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.
Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Мы скоро докажем обе этих теоремы, а пока твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь?
А вот представь, что у тебя задача:
Дано: \( AB=5,
Найти: \( \displaystyle BC. \)
Ты тут же соображаешь, \(\displaystyle BD \) биссектриса и, о чудо, она разделила сторону \( \displaystyle AC \) пополам! (по условию…).
Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.
Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике
Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Смотри: у \( \triangle ABL \) и \( \triangle CBL \) равны стороны \( AB \) и \( BC \), сторона \( BL \) у них вообще общая и \( \angle 1=\angle 2\). (\( BL \) – биссектриса!)
И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что \( \triangle ABL=\triangle CBL \), а значит \( AL \)= \( CL \) и \( \angle 3=\angle 4 \).
\( AL \) = \( CL \) – это уже хорошо – значит, \( BL \) оказалась медианой.
А вот что такое \( \angle 3=\angle 4 \)?
Читать далее…
Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:
Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.
Биссектриса, медиана, высота — определения и отличия
Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?
Если нет, не страшно. Сейчас разберемся.
Чем биссектриса, медиана и высота похожи между собой?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
Чем биссектриса, медиана и высота отличаются между собой?
Вернемся к нашим баранам — к свойствам биссектрисы…
Угол между биссектрисами любого треугольника
B \( \triangle ABC \)проведем две биссектрисы \( AO \)и \( OC \).
Они пересеклись. Какой же угол получился у точки \( O \)?
Применим этот потрясающий факт. С одной стороны, из \( \triangle ABC \):
\( \angle A+\angle B+\angle C=180<>^\circ \), то есть \( \angle B=180<>^\circ \text< >-\text< >\left( \angle A+\angle C \right) \).
Теперь посмотрим на \( \triangle AOC \):
\( \angle 2+\angle 6+\angle 3=180<>^\circ \)
Но биссектрисы, биссектрисы же!
Значит \( \left( \triangle AOC \right) \)
Теперь через буквы
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?
Равнобедренный треугольник: свойства, признаки и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Для доказательства следующих теорем нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
В каждом из доказательств мы пользуемся признаком равенства треугольников, вот и повод их повторить.
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.


















