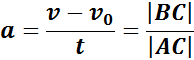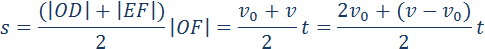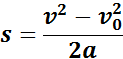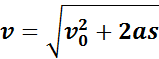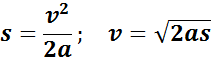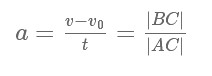Как доказать на практике что движение равноускоренное
Равноускоренное движение
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 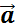
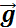
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 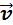
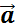
Проекции векторов скорости 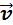
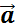
При равноускоренном прямолинейном движении скорость тела определяется формулой
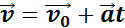
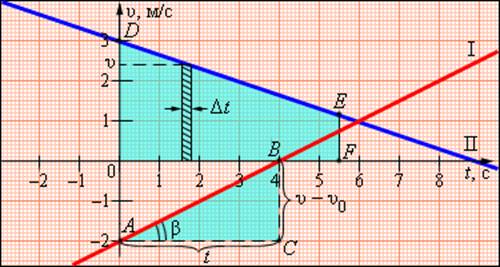
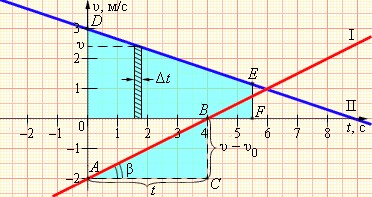
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).
Графики скорости равноускоренного движения
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с 2
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
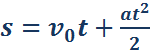
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
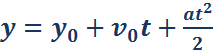
Это выражение называют законом равноускоренного движения.
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
Если начальная скорость υ0 равна нулю, эти формулы принимают вид
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
Равноускоренное движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.
Зависимость скорости от времени.
При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
Закон движения.
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:
Подставляем сюда выражение для скорости, даваемое формулой (3) :
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
Прямолинейное равноускоренное движение.
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
и подставим в формулу для перемещения:
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
Свободное падение.
Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи км.
Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Горизонтальный бросок.
Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.
 |
| Рис. 1. Горизонтальный бросок |
Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:
Бросок под углом к горизонту.
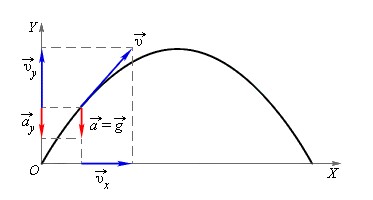
Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.
 |
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
Равноускоренное движение: формулы и примеры
Содержание:
Определение
Равноускоренным движением в физике считается такое движение, вектор ускорения которого не меняется по модулю и направлению. Говоря простым языком, равноускоренное движение представляет собой неравномерное движение (то есть идущее с разной скоростью), ускорение которого является постоянным на протяжении определенного промежутка времени. Представим себе автомобиль, который начинает двигаться, первые 2 секунды его скорость равна 10 м/с, следующие 2 секунды он уже движется со скоростью 20 м/с, а еще через 2 секунды уже со скоростью 30 м/с. То есть каждые 2 секунды он ускоряется на 10 м/с, такое движение и есть равноускоренным.
Отсюда можно вывести предельно простое определение равноускоренного движения: это такое движение любого физического тела, при котором его скорость за равные промежутки времени изменяется одинаково.
Примеры
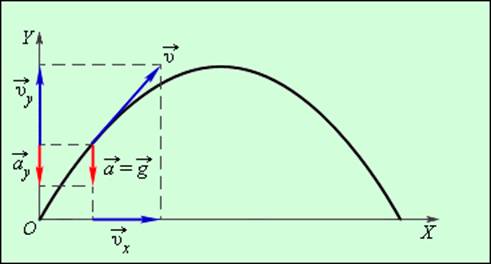
Наглядным примером равноускоренного движения в повседневной жизни может быть велосипед, едущий с горки вниз (но не велосипед, управляемый велосипедистом), или брошенный камень под определенным углом к горизонту.
К слову пример с камнем можно рассмотреть более детально. В любой точке траектории полета на камень действует ускорение свободного падения g. Ускорение g не меняется, то есть остается константой и всегда направлено в одну сторону (по сути, это главное условие равноускоренного движения).
Полет брошенного камня удобно представить в виде сумы движений относительно вертикальной и горизонтальной оси системы координат.
Если вдоль оси Х движение камня будет равномерным и прямолинейным, то вдоль оси Y равноускоренным и прямолинейным.
Формула
Формула скорости при равноускоренном движении будет иметь такой вид:
Где V0 – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.
При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.
Ускорение может быть определено по углу наклона графика скорости. На этом рисунке оно равно отношению сторон треугольника АВС.
Чем больше угол β, тем больше наклон и как следствие, крутизна графика по отношению к оси времени, и тем больше будет ускорение тела.
Рекомендуемая литература по теме
Видео
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.
Похожие посты:
Один комментарий
Уравнения равноускоренного движения
При постоянном ускорении скорость физического тела равномерно возрастает, начиная с нуля.
Расстояние, пройденное равноускоренным телом, начиная с нулевой скорости, пропорционально квадрату времени.
Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял — в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки.
Движение физических тел изучалось с незапамятных времен, и основы кинематики были заложены задолго до рождения Галилея. Элементарные задачи описания движения сегодня изучают уже в начальной школе. Например, все знают, что если автомобиль равномерно движется со скоростью 20 км/ч, то за 1 час он проедет 20 км, за 2 часа — 40 км, за 3 часа — 60 км и т. д. И до тех пор, пока машина движется с постоянной скоростью (стрелка спидометра не отклоняется от заданного деления на его шкале), рассчитать пройденное расстояние труда не составляет — достаточно умножить скорость машины на время, которое она находится в пути. Этот факт известен настолько давно, что имя его первооткрывателя наглухо затерялось в тумане античных времен.
Сложности возникают, как только объект начинает двигаться с переменной скоростью. Трогаетесь вы, к примеру, от светофора — и стрелка спидометра ползет от нуля вверх, пока вы не отпустите педаль газа и не нажмете педаль тормоза. На самом деле стрелка спидометра на месте практически не стоит — она всё время движется вверх или вниз. В начале каждой отдельно взятой секунды реальная скорость машины одна, а в конце секунды — уже другая, и пройденный ею за секунду путь точно рассчитать не так-то просто. Эта проблема — описание движения с ускорением — волновала естествоиспытателей задолго до Галилея.
Сам же Галилео Галилей подошел к ней новаторски и, фактически, задал направление всего дальнейшего развития современной методологии естествознания. Вместо того чтобы сидеть и умозрительно решать вопрос о движении ускоряющихся тел, он придумал гениальные по своей простоте опыты, позволяющие экспериментально проследить, что в действительности происходит с ускоряющимися телами. Нам может показаться, что ничего особенно новаторского в таком подходе нет, однако до Галилея основным методом решения проблем «натурфилософии» — о чем говорит само название тогдашней естественной науки — было умозрительное осмысление происходящего, а не его экспериментальная проверка. Сама идея проведения физических экспериментов была в то время по-настоящему радикальной. Чтобы понять идею опытов Галилея, представьте себе тело, падающее под воздействием силы земного притяжения. Выпустите какой-нибудь предмет из рук — и он упадет на пол; при этом в первое мгновение скорость его движения будет равна нулю, но он тут же начнет ускоряться — и будет продолжать ускоряться, пока не упадет на землю. Если мы сможем описать падение предмета на землю, мы затем сможем распространить это описание и на общий случай равноускоренного движения.
Сегодня измерить динамику падения предмета не сложно — можно с большой точностью зафиксировать время от начала падения до любой промежуточной точки. Однако во времена Галилея точных секундомеров не было, да и любые механические часы по современным стандартам были весьма примитивны и неточны. Поэтому ученый первым делом разработал экспериментальный аппарат, позволяющий обойти эту проблему. Во-первых, он «разбавил» силу тяжести, замедлив время падения до разумных, с точки зрения имеющихся инструментов измерения, пределов, а именно — заставил тела скатываться по наклонной плоскости, а не просто падать отвесно. Затем он придумал, как обойти неточность современных ему механических часов, натянув на пути скатывающегося по наклонной поверхности шара ряд струн, чтобы он задевал их по дороге и можно было хронометрировать его движение по извлекаемым звукам. Раз за разом спуская шар по наклонной под рядом струн, Галилей перемещал струны, пока не добился, чтобы шар на всем своем пути, задевая натянутые струны, извлекал звуки через равные промежутки времени.
В конце концов Галилею удалось накопить достаточный объем экспериментальной информации о равноускоренном движении. Тело, стартующее из состояния покоя, далее движется так, как это описано в самом начале данной статьи. В переводе на язык математических символов равноускоренное движение описывается следующими уравнениями:
где a — ускорение, v — скорость, d — расстояние, пройденное телом за время t. Чтобы прочувствовать смысл этих уравнений, достаточно пристально пронаблюдать за падением предметов. Скорость падения зримо возрастает со временем, прошедшим с начала падения. Это следует из первого уравнения. Очевидно и то, что в процессе падения на прохождение первой части пути у тела уходит больше времени, чем на оставшуюся часть пути. Именно это и описывает вторая формула, поскольку из неё следует, что чем дольше тело ускоряется, тем больший отрезок пути оно преодолевает за одно и то же время.
Галилей сделал и еще одно важное наблюдение о теле, находящемся в состоянии свободного падения под воздействием силы гравитационного притяжения, хотя и не смог подтвердить его непосредственными измерениями. Экстраполировав результаты, полученные им при наблюдении скатывающихся по наклонной плоскости предметов, он сумел определить ускорение свободного падения тела на поверхность Земли. Ускорение свободного падения принято обозначать g, и оно равняется (приблизительно):
g = 9,8 м/с 2 (метра в секунду за секунду)
То есть, если уронить предмет из состояния покоя, за каждую секунду падения его скорость будет возрастать на 9,8 метра в секунду. На исходе первой секунды падения тело будет двигаться со скоростью 9,8 м/с, на исходе второй — со скоростью 2 × 9,8 = 18,6 м/с и так далее. Величина g определяет коэффициент ускорения падения тела, находящегося в непосредственной близости от земной поверхности, в связи с чем g принято называть ускорением свободного падения, или гравитационным ускорением.
Здесь следует сделать два важных замечания относительно полученных Галилеем результатов. Во-первых, ученый получил чисто экспериментальное значение величины g, ни на каких теоретических прогнозах не основывающееся. Значительно позже Исаак Ньютон в своих знаменитых работах показал, что величину g можно рассчитать теоретически, исходя из сочетания сформулированных им законов механики Ньютона и закона всемирного тяготения Ньютона. Именно первопроходческий труд Галилея и проложил дорогу последующим триумфальным открытиям Ньютона и формированию классической механики в её общеизвестном виде.
Второй важнейший момент состоит в том, что ускорение свободного падения не зависит от массы падающего тела. По сути, сила притяжения пропорциональна массе тела, но это полностью компенсируется большей инерцией, присущей более массивному телу (его нежеланию двигаться, если хотите), а посему (если не учитывать сопротивление воздуха) все тела падают с одинаковым ускорением. Это практическое заключение вступало в полное противоречие с умозрительными предсказаниями древних и средневековых натурфилософов, которые были уверены, что всякой вещи свойственно стремиться к центру мироздания (коим им, естественно, представлялся центр Земли) и что чем массивнее предмет, тем с большей скоростью он к этому центру устремляется.
Свое видение Галилей, конечно же, подкрепил экспериментальными данными, но вот опыта, который ему традиционно приписывают, он, скорее всего, вовсе не проводил. Согласно околонаучному фольклору, он сбрасывал предметы различной массы с «падающей» Пизанской башни, чтобы продемонстрировать, что они достигают поверхности земли одновременно. В этом случае, однако, Галилея ждало бы разочарование, поскольку более тяжелые предметы неизбежно падали бы на землю раньше легких из-за разницы в удельном сопротивлении воздуха. Если бы сбрасываемые с башни предметы были одного размера, сила сопротивления воздуха, тормозящая их падение, была бы одинаковой для всех предметов. При этом из законов Ньютона следует, что более легкие предметы затормаживались бы воздухом интенсивнее тяжелых и падали на землю позднее тяжелых предметов. А это, естественно, противоречило бы предсказанию Галилея.
10 класс
§ 7. Ускорение. Равноускоренное прямолинейное движение
Среднее ускорение.
Введём ещё одну физическую величину, описывающую механическое движение, — ускорение. Оно характеризует быстроту изменения скорости движения тела. Ускорение является важнейшей физической величиной, так как действия одних тел на другие определяют не скорости тел, а быстроту изменения скоростей.
Среднее ускорение cp за промежуток времени Δt равно:
Если ускорение постоянно, то его можно вычислять как изменение скорости в единицу времени. Это позволяет установить единицу ускорения в СИ — метр на секунду в квадрате (м/с 2 ).
Мгновенное ускорение.
На практике нужно уметь определять ускорение в каждой точке траектории. Это ускорение называют мгновенным. На разных участках траектории за одинаковые промежутки времени Δt изменение скорости Δ может быть различным как по модулю, так и по направлению. При уменьшении интервала времени Δt изменения скорости Δ уменьшаются по модулю и меняются по направлению (рис. 2.27).
Соответственно, средние ускорения также меняются по модулю и по направлению. Но по мере приближения интервала Δt к нулю отношение Δ / Δt стремится к определённому предельному значению. Это предельное значение и есть мгновенное ускорение, или просто ускорение.
В то время как мгновенная скорость тела направлена по касательной к траектории, направление ускорения совпадает с направлением изменения скорости Δ за малый промежуток времени. Изменение же скорости только при прямолинейном движении совпадает с направлением самой скорости или противоположно ему. Поэтому ускорение может быть направлено под различными углами по отношению к траектории.
Равноускоренное прямолинейное движение.
Движение тела называют равноускоренным, если его ускорение остаётся постоянным, т. е. не изменяется с течением времени (как по модулю, так и по направлению).
Равноускоренное движение может быть как прямолинейным, так и криволинейным. Далее мы рассмотрим равноускоренное прямолинейное движение.
Для равноускоренного движения в одной плоскости уравнению (1) будут соответствовать две формулы для проекций вектора скорости на оси X и Y:
Графическое представление равноускоренного прямолинейного движения.
Если тело движется равноускоренно, то графиками модуля и проекции ускорения будут прямые, параллельные оси времени. Важно понимать, что модуль — неотрицательная величина, поэтому график модуля ускорения не может быть расположен ниже оси времени (рис. 2.28).
В то же время проекции ускорения могут иметь как положительные (рис. 2.29, а), так и отрицательные значения (рис. 2.29, б).
Из рисунка 2.29, б следует, что ускорение направлено противоположно оси X. По графику проекции ускорения можно найти, кроме αх, изменение проекции скорости Δυx. Оно численно равно площади прямоугольника OABC или OKMN, так как Δυx = αхt, а произведение axt численно равно площади прямоугольника OABC или OKMN.
Значение площади берётся со знаком «минус», если она расположена ниже оси времени, что соответствует рисунку 2.29, б, где Δυx = αхt 0, то α1х > 0. Второе тело движется противоположно оси X и так как Δυx 0) с равномерно уменьшающимся до нуля (остановка) значением проекции скорости. После этого проекция скорости становится отрицательной. Это означает, что тело стало двигаться в направлении, противоположном положительному направлению оси X. Проекция ускорения тела отрицательна. Так как проекция скорости точки равномерно убывает, то проекция ускорения остаётся постоянной. Следовательно, тело движется равноускоренно.
Координата и радиус-вектор при равноускоренном движении
Запишем уравнение для одной из координат движущегося тела:
В случае равноускоренного движения изменение координаты можно определить с помощью графика зависимости проекции скорости от времени. Ранее мы показали, что изменение координаты Δx при равномерном прямолинейном движении можно найти по площади прямоугольника под графиком проекции скорости:
Задача упрощалась тем, что υx = const.
При движении с постоянным ускорением проекция скорости тела изменяется в зависимости от времени по линейному закону. В курсе физики 9 класса было получено выражение для изменения координаты тела:
Подставляя значения изменения координат в кинематические уравнения: х = x0 + Δx, y = y0 + Δy, получим выражения для координат при движении тела с постоянным ускорением как функции времени:
Формулы (2) применимы для описания как прямолинейного движения (в этом случае целесообразно ось X направить по прямой, вдоль которой движется тело), так и криволинейного движения. Важно лишь, чтобы оно было равноускоренным.
Двум уравнениям (2) соответствует одно векторное уравнение:
Отметим, что при помощи уравнений (2) или (3) можно найти только положение движущегося тела в любой момент времени, но не пройденный путь. При равноускоренном прямолинейном движении возможно изменение направления скорости на противоположное (например, при движении брошенного вверх тела). В таком случае нужно определить, в какой точке траектории произошло изменение направления скорости. Путь находится в результате суммирования длин отрезков траектории, пройденных телом за указанное время.
Вопросы:
1. Как можно определить среднее ускорение?
2. Какое движение тела называют равноускоренным прямолинейным?
3. Запишите выражение для скорости движения тела при равноускоренном прямолинейном движении.
4. Как можно определить координаты тела, совершающего равноускоренное движение?
5. Какую информацию можно получить, анализируя графики равноускоренного прямолинейного движения?
Вопросы для обсуждения:
2. На рисунке 2.33 приведены графики зависимости проекции скорости υx от времени t для тел 1 и 2. Как изменяются модули скоростей тел? Чему соответствуют отрезки ОС и OD?
3. В трактате «Беседы и математические доказательства, касающиеся двух новых отраслей науки» (1638) Галилей приводит определения двух видов движения тел:
а) «. движением я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собою»;
б) «. движением называется такое, при котором после выхода из состояния покоя в равные промежутки времени прибавляются и равные приращения скорости».
О каких видах движения идёт речь в первом и во втором случаях?
Пример решения задачи
Ружейная пуля движется равноускоренно внутри ствола длиной 0,6 м в течение 0,004 с. Найдите модуль скорости пули при вылете из ствола ружья и модуль ускорения её движения внутри ствола. Модуль начальной скорости движения пули считайте равным нулю.
Запишем кинематическое уравнение для пули: x(t) = αt 2 / 2 (так как υ0 = 0 по условию задачи).
В момент вылета пули из ствола ружья (рис. 2.34) t = τ x(τ) = l. C учётом этого получим:
Подставим числовые данные:
α = 2 • 0,6 / 0,004 2 м/с 2 = 75000 м/с 2 = 75 км/с 2
Найдём модуль скорости вылета υп пули:
υп = ατ; υп = 75000 • 0,004 м/с = 300 м/с.
Ответ: υп = 300 м/с, α = 75 км/с 2
Упражнения:
1. Какой должна быть длина взлётной полосы, если самолёт для взлёта должен приобрести скорость, равную 240 км/ч, за 30 с?
2. Автомобиль, двигаясь равноускоренно и прямолинейно, через 10 с после начала движения достиг скорости, модуль которой равен 36 км/ч. Определите модуль ускорения, с которым двигался автомобиль.
Какой путь он прошёл:
б) за последнюю секунду движения?
4. Космическая ракета разгоняется из состояния покоя и, пройдя путь 200 км, достигает скорости, модуль которой равен 11 км/с. C каким по модулю ускорением она двигалась? Чему равно время разгона ракеты?
5. Покажите, что при равноускоренном движении по заданным значениям υ0x, υx и αx можно определить проекцию перемещения sx по