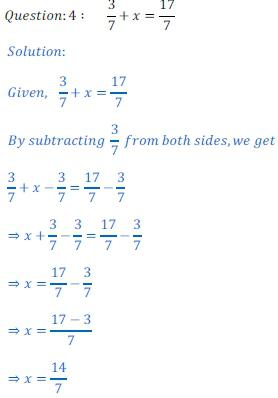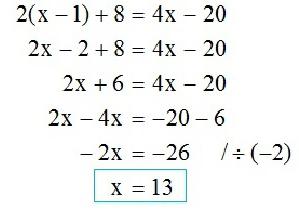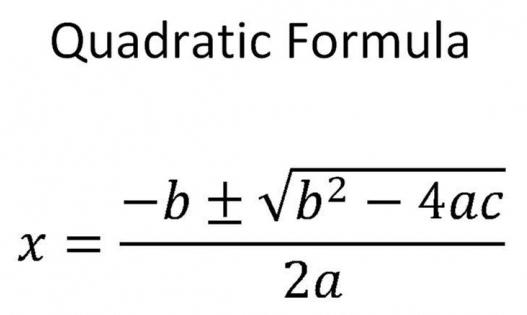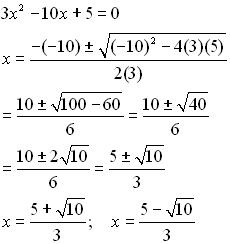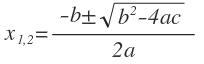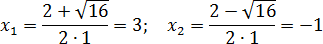Как найти чему равен корень уравнения
Найти корень уравнения? Это просто!
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Неполные квадратные уравнения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.
Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три формулы неполных квадратных уравнений:
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
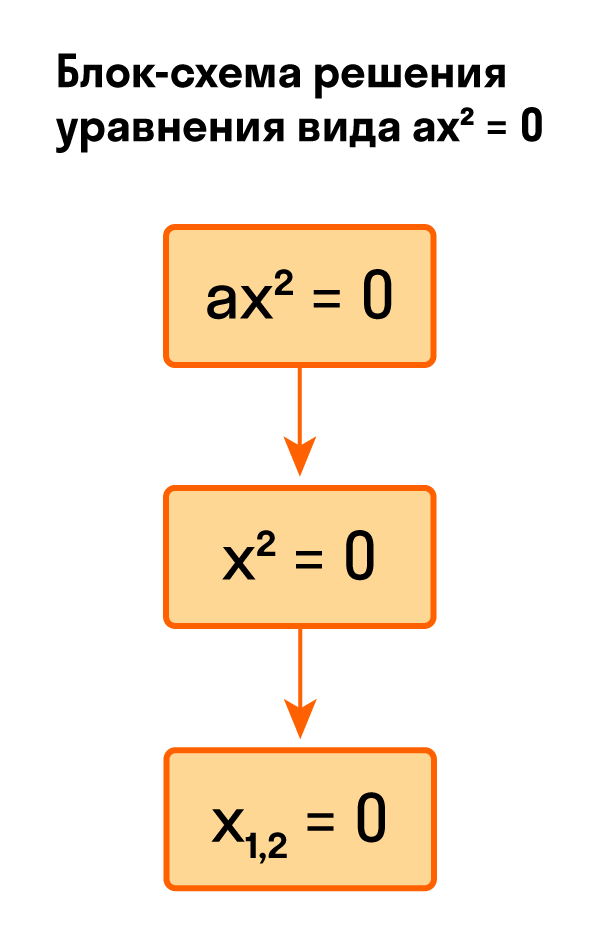
Как решить уравнение ax² = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.
Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.
Пример 1. Решить −5x² = 0.
Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!
Как решить уравнение ax² + с = 0
Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:
В двух словах
Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:
Пример 1. Найти решение уравнения 9x² + 4 = 0.
Ответ: уравнение 9x² + 4 = 0 не имеет корней.
Как решить уравнение ax² + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.
Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:
Ответ: х = 0 и х = 16.
Разложить левую часть уравнения на множители и найти корни:
Как найти дискриминант квадратного уравнения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие квадратного уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 8 + 4 = 12. При вычислении левой части получается верное числовое равенство, то есть 12 = 12.
Уравнением можно назвать выражение 8 + x = 12, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени, значит, такое уравнение является квадратным.
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Есть три вида квадратных уравнений:
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Чаще всего для поиска дискриминанта используют формулу:
В этом ключе универсальная формула для поиска корней квадратного уравнения выглядит так:
Эта формула подходит даже для неполных квадратных уравнений.
Но есть и другие формулы — все зависит от вида уравнения. Чтобы в них не запутаться, сохраняйте табличку или распечатайте ее и храните в учебнике.
Как решать квадратные уравнения через дискриминант
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный. Только после этого вычисляем значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
А вот и еще одна табличка: в ней вы найдете формулы для поиска корней квадратных уравнений при помощи дискриминанта:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, важно практиковаться. Вперед!
Примеры решения квадратных уравнений с помощью дискриминанта
Ответ: корень уравнения 3.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
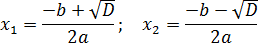
Первое уравнение:
x 2 − 2 x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2 x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
Наконец, третье уравнение:
x 2 + 12 x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид a x 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
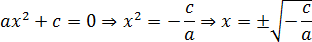
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (− c / a ) ≥ 0. Вывод:
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
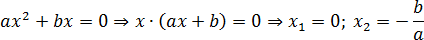
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7 x = 0 ⇒ x · ( x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5 x 2 + 30 = 0 ⇒ 5 x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4 x 2 − 9 = 0 ⇒ 4 x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Решение квадратных уравнений: формула корней, примеры
В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.
Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.
Квадратное уравнение, его виды
Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.
Приведенные и неприведенные квадратные уравнения
По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.
Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.
Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.
Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.
Решение
Полные и неполные квадратные уравнения
В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.
Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.
Порассуждаем, почему типам квадратных уравнений даны именно такие названия.
Решение неполных квадратных уравнений
Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:
Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.
Решение уравнения a·x 2 =0
Кратко решение оформляется так:
Решение уравнения a · x 2 + c = 0
Резюмируем все рассуждения выше.
Решение
Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.
Решение
Решение уравнения a·x 2 +b·x=0
Закрепим материал примером.
Решение
Кратко решение уравнения запишем так:
Дискриминант, формула корней квадратного уравнения
Для нахождения решения квадратных уравнений существует формула корней:
Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.
Вывод формулы корней квадратного уравнения
Вновь сформулируем выводы:
Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:
Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.
Алгоритм решения квадратных уравнений по формулам корней
Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.
В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.
Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.
Примеры решения квадратных уравнений
Приведем решение примеров при различных значениях дискриминанта.
Решение
Решение
Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0
Решение
В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:
В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.
Формула корней для четных вторых коэффициентов
Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:
Решение
Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.
Упрощение вида квадратных уравнений
Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.
Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Связь между корнями и коэффициентами
Самыми известными и применимыми являются формулы теоремы Виета:
Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты: