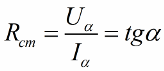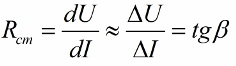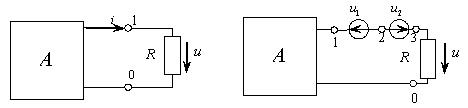Линейные и нелинейные элементы электрической цепи

Те элементы электрической цепи, для которых зависимость тока от напряжения I(U) или напряжения от тока U(I), а также сопротивление R, постоянны, называются линейными элементами электрической цепи. Соответственно и цепь, состоящая из таких элементов, именуется линейной электрической цепью.

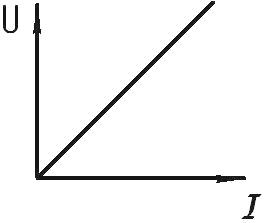
Для линейных элементов характерна линейная симметричная вольт-амперная характеристика (ВАХ), выглядящая как прямая линия, проходящая через начало координат под определенным углом к координатным осям. Это свидетельствует о том, что для линейных элементов и для линейных электрических цепей закон Ома строго выполняется.

Яркий пример линейного элемента — проволочный резистор. Ток через такой резистор в определенном диапазоне рабочих напряжений линейно зависит от величины сопротивления и от приложенного к резистору напряжения.

Характеристика проводника (вольтамперная характеристика) — зависимость между напряжением, подводимым к проводнику, и силой тока в нем (обычно выраженная в виде графика).

Для металлического проводника, например, сила тока в нем пропорциональна приложенному напряжению, и поэтому характеристика представляет собой прямую линию. Чем круче идет прямая, тем меньше сопротивление проводника. Однако некоторые проводники, в которых ток не пропорционален приложенному напряжению (например, газоразрядные лампы), имеют более сложную, не прямолинейную вольтамперную характеристику.

Если же для элемента электрической цепи зависимость тока от напряжения или напряжения от тока, а также сопротивление R, непостоянны, то есть изменяются в зависимости от тока или от приложенного напряжения, то такие элементы называются нелинейными, и соответственно электрическая цепь, содержащая минимум один нелинейный элемент, окажется нелинейной электрической цепью.

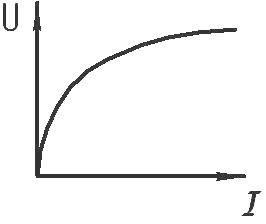
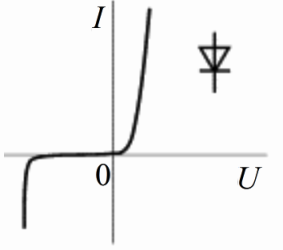
Вольт-амперная характеристика нелинейного элемента уже не является прямой линией на графике, она непрямолинейна и часто несимметрична, как например у полупроводникового диода. Для нелинейных элементов электрической цепи закон Ома не выполняется.

В данном контексте речь может идти не только о лампе накаливания или о полупроводниковом приборе, но и о нелинейных индуктивностях и емкостях, у которых магнитный поток Ф и заряд q нелинейно связаны с током катушки или с напряжением между обкладками конденсатора. Поэтому для них вебер-амперные характеристики и кулон-вольтные характеристики будут нелинейными, они задаются таблицами, графиками или аналитическими функциями.

Пример нелинейного элемента — лампа накаливания. С ростом тока через нить накаливания лампы, ее температура увеличивается и сопротивление возрастает, а значит оно непостоянно, и следовательно данный элемент электрической цепи нелинеен.

Такой подход делает возможным простейший анализ и расчет простых нелинейных цепей.

На рисунке выше показана ВАХ типичного диода. Она располагается в первом и в третьем квадрантах координатной плоскости, это говорит нам о том, что при положительном или отрицательном приложенном к p-n-переходу диода напряжении (в том или ином направлении) будет иметь место прямое либо обратное смещение p-n-перехода диода. С ростом напряжения на диоде в любом из направлений ток сначала слабо увеличивается, а после резко возрастает. По этой причине диод относится к неуправляемым нелинейным двухполюсникам.

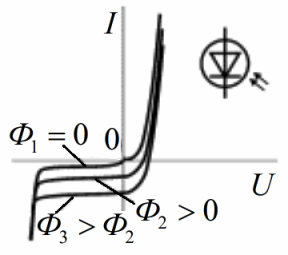
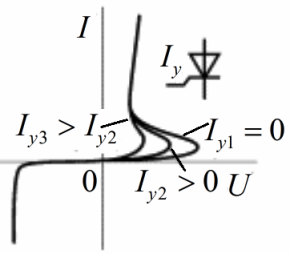
Это ВАХ тиристора, здесь видна ее явная зависимость от величины тока управляющего электрода. В первом квадранте — рабочий участок тиристора. В третьем квадранте начало ВАХ — малый ток и большое приложенное напряжение (в запертом состоянии сопротивление тиристора очень велико). В первом квадранте ток велик, падение напряжения мало — тиристор в данный момент открыт.

Момент перехода из закрытого — в открытое состояние наступает тогда, когда на управляющий электрод подан определенный ток. Переключение из открытого состояния — в закрытое происходит при снижении тока через тиристор. Таким образом, тиристор — это управляемый нелинейный трехполюсник (как и транзистор, у которого ток коллектора зависит от тока базы).

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Также двухполюсники можно разделить на линейные (содержат только линейные элементы) и нелинейные. У линейных двухполюсников свойства не зависят от величин токов и напряжений в двухполюснике.

Также можно произвести деление двухполюсников на активные и пассивные. Активные двухполюсники отдают больше энергии, чем потребляют; пассивные двухполюсники больше потребляют, чем отдают или столько же отдают. В данном случае вводят понятие средней мощности за период: Для пассивных двухполюсников , а для активных .

По элементам можно разделить двухполюсники с элементами с сосредоточенными параметрами (R, L, C элементы) и с распределенными параметрами (например, длинными линиями).

Можно выделить двухполюсники без потерь энергии (реактивные, содержащие L, C элементы), двухполюсники с малыми потерями (содержат катушки индуктивности, конденсаторы) и двухполюсники с потерями энергии (диссипативные, т.е. содержат резисторы).

В общем случае при нахождении характеристик двухполюсников используют операторные функции, т.е. операторное напряжение и операторный ток.

Операторное сопротивление двухполюсника и его свойства

Под операторным сопротивлением двухполюсника понимают отношение операторного изображения напряжения к операторному изображению тока через двухполюсник (обычно при нулевых независимых начальных условиях).

Операторное сопротивление представляет собой некоторую функцию комплексной переменной . Эта функция зависит от типа двухполюсника. Она может быть трансцендентной функцией, если в двухполюснике имеется участок с распределенными параметрами, и рациональной, если таких участков нет.

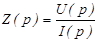
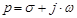
В дальнейшем будем рассматривать только двухполюсники без участков с распределенными параметрами.

Если при каком-то значении комплексной переменной p сопротивление , то это называется нулем сопротивления двухполюсника. Если при каком-то p сопротивление , то это называется полюсом.

Для пассивных двухполюсников все нули и полюсы располагаются в левой полуплоскости комплексной переменной p. В крайнем случае могут быть нули и полюсы на мнимой оси. Полиномы, у которых нули располагаются в левой полуплоскости, называют полиномами Гурвица.

Если двухполюсник пассивный, то цепь будет устойчивой; если двухполюсник активный, то цепь может быть и неустойчивой.

Для пассивных двухполюсников функция сопротивления или проводимости является положительной вещественной функцией. Она вещественна, если p – вещественная величина, ее вещественная часть положительна, если положительна вещественная часть p.

Из операторного сопротивления можно получить комплексное:

Для пассивных двухполюсников , а для активных может выполняться соотношение: .

Функции являются частотными характеристиками. Используя определенный математический аппарат от операторных функций можно перейти к временным функциям и получить временные характеристики двухполюсника, которые оценивают реакцию двухполюсника на стандартное воздействие. Для пассивного двухполюсника по свободным составляющим эта реакция должна носить затухающий характер, т.е. стремиться к 0 (за исключением крайнего случая, когда какие-то нули или полюсы располагаются на мнимой оси).

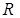
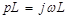
Простейшие двухполюсники имеют сопротивления , , . Сложные двухполюсники составляются из различных комбинаций простых.

Активные двухполюсники содержат по схемам замещения управляемые или зависимые источники. Автономные двухполюсники содержат независимые источники.

Реактивные двухполюсники

Реактивные двухполюсники содержат только реактивные элементы (L и C). В принципе они неавтономные и могут быть линейными и нелинейными. Эти двухполюсники относят к разряду пассивных, так как они, сколько получают энергии, столько отдают. Соответственно все нули и полюсы располагаются на мнимой оси.

Практически, для реальных цепей реактивные двухполюсники – это двухполюсники из катушек индуктивности и конденсаторов (двухполюсники с малыми потерями).

Простейшие реактивные двухполюсники

Схемы простейших реактивных двухполюсников:

Таблица 1. Простейшие реактивные двухполюсники

И их свойства

У всех реактивных двухполюсников комплексное сопротивление чисто мнимое: . Соответственно мнимая часть или реактивное сопротивление характеризует частотные свойства двухполюсника.

Иногда вместо графиков сопротивлений изображают характеристические оси:

Значение величины сопротивления реактивного двухполюсника в крайних точках, на крайних частотах 0 и ∞ называют классом реактивного двухполюсника.

Источник

№8 Пассивный и активный двухполюсники. Теорема об активном двухполюснике.

Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов).

Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным. Если в схеме двухполюсника имеются нескомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 8.1). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.

Пассивный двухполюсник является потребителем энергии и может быть заменен эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 8.2).

Активный двухполюсник ведет себя как генератор. Находящиеся внутри него нескомпенсированные источники отдают энергию во внешнюю цепь (рис. 8.3, а). Можно попытаться подобрать источник энергии с ЭДС ЕЭ и внутренним сопротивлением RЭ, который будет эквивалентен двухполюснику, то есть будет создавать во внешней цепи тот же самый ток (рис. 8.3, б).

Полученный генератор должен быть эквивалентен двухполюснику в любом режиме, в том числе и в режимах холостого хода и короткого замыкания. Источники энергии, входящие в состав активного двухполюсника, в режиме холостого хода создают на его зажимах напряжение UХ (рис. 8.4, а), а при коротком замыкании вызывают ток IK (рис. 8.4, б).

Из схем, приведенных на рис. 8.4, следует:

Итак, любой активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого ЕЭ равна напряжению холостого хода двухполюсника, а внутреннее сопротивление RЭ напряжению холостого хода, деленному на ток короткого замыкания.

Это утверждение и есть теорема об активном двухполюснике (эквивалентном генераторе).

Пример 1.4. Заменить активный двухполюсник, выделенный пунктиром на рис. 8.5, а, эквивалентным генератором (рис. 8.5, б). Численные значения параметров цепи составляют: Е1 = 200 В, Е2 = 100 В, R1 = 50 Ом, R2 = 20 Ом, R3 = 20 Ом.

Р е ш е н и е. Напряжение холостого хода, определяющее величину ЭДС эквивалентного генератора, можно найти по схеме на рис. 8.6, а любым известным способом.

Воспользуемся, например, методом контурных токов. Принимая в качестве контурных токи I1Х для левого контура и I3Х для правого, записываем контурные уравнения, из которых определяем контурные токи:

Напряжение холостого хода – это напряжение между точками m и n. Оно равно падению напряжения на сопротивлении R3:

Применим теперь метод узловых потенциалов.

Принимая потенциал узла n равным нулю (φn = 0), для узла m запишем узловое уравнение:

Из уравнения (1.12) имеем:

Получили тот же самый результат.

Приступаем к расчету режима короткого замыкания. Ток IK в схеме на рис. 8.6, б найдем методом наложения. При действии только первой ЭДС ее ток проходит по первой ветви и, минуя вторую и третью ветви, замыкается по проводнику, закорачивающему зажимы двухполюсника:

Аналогично находим ток, вызываем второй ЭДС:

Ток в третьей ветви равен нулю, так как она закорочена. Поэтому:

В соответствии с теоремой об эквивалентном генераторе

Источник

Пассивный и активный двухполюсники

Пассивный и активный двухполюсники. Теорема об активном двухполюснике

Двухполюсником называется часть электрической цепи любой сложности и произвольной конфигурации, выделенная относительно двух зажимов (двух полюсов). Двухполюсник, не содержащий источников энергии или содержащий скомпенсированные источники (суммарное действие которых равно нулю), называется пассивным.

Если в схеме двухполюсника имеются не скомпенсированные источники, он называется активным. На схеме двухполюсник обозначают прямоугольником с двумя выводами (рис. 1.14). Это обозначение можно условно рассматривать как коробку, внутри которой находится электрическая цепь.

Пассивный двухполюсник является потребителем энергии и может быть заменен

эквивалентным сопротивлением, величина которого равна входному сопротивлению двухполюсника (см., например, рис. 1.15).

Активный двухполюсник ведет себя как генератор. Находящиеся внутри него нескомпенсированные источники отдают энергию во внешнюю цепь (рис. 1.16, а). Можно попытаться подобрать источник энергии с ЭДС Е_Э и внутренним сопротивлением R_Э, который будет эквивалентен двухполюснику, то есть будет создавать во внешней цепи тот же самый ток (рис. 1.16, б).

Полученный генератор должен быть эквивалентен двухполюснику в любом режиме, в том числе и в режимах холостого хода и короткого замыкания. Источники энергии, входящие в состав активного двухполюсника, в режиме холостого хода создают на его зажимах напряжение U_Х (рис. 1.17, а), а при коротком замыкании вызывают ток I_K (рис. 1.17, б).

Из схем, приведенных на рис. 1.17, следует:

То есть, любой активный двухполюсник может быть заменен эквивалентным генератором, ЭДС которого Е_Э равна напряжению холостого хода двухполюсника, а внутреннее сопротивление R_Э напряжению холостого хода, деленному на ток короткого замыкания.

Это утверждение и есть теорема об активном двухполюснике (эквивалентном генераторе).

Пример 1.4. Заменить активный двухполюсник, выделенный пунктиром на рис. 1.18, а, эквивалентным генератором (рис. 1.18, б). Численные значения параметров цепи составляют: Е₁ = 200 В, Е₂ = 100 В, R₁ = 50 Ом, R₂ = 20 Ом, R₃ = 20 Ом.

Рис. 1.18. Замена активного двухполюсника (а) эквивалентным генератором (б).

Решение. Напряжение холостого хода, определяющее величину ЭДС эквивалентного генератора, можно найти по схеме на рис. 1.19, а любым известным способом.

Рис. 1.19. Режимы холостого хода (а) и короткого замыкания (б)

Воспользуемся, например, методом контурных токов. Принимая в качестве контурных токи I_1Х для левого контура и I_3Х для правого, записываем контурные уравнения, из которых определяем контурные токи:

Напряжение холостого хода – это напряжение между точками m и n. Оно равно падению напряжения на сопротивлении R₃:

Таким образом, ЭДС эквивалентного генератора Е_Э = 75 В.

Применим теперь метод узловых потенциалов.

Принимая потенциал узла n равным нулю (j _n = 0), для узла m запишем узловое уравнение:

(1.12)

Из уравнения (1.12) имеем:

Получили тот же самый результат.

Приступаем к расчету режима короткого замыкания. Ток I_K в схеме на рис. 1.19, б найдем методом наложения. При действии только первой ЭДС ее ток проходит по первой ветви и, минуя вторую и третью ветви, замыкается по проводнику, закорачивающему зажимы двухполюсника:

Аналогично находим ток, вызываемый второй ЭДС:

Ток в третьей ветви равен нулю, так как она закорочена.

В соответствии с теоремой об эквивалентном генераторе

Источник

Основы теории двухполюсников

Двухполюсником называется электрическая цепь (или часть ЭЦ), имеющая два зажима (вывода, полюса) для подключения к внешней цепи (остальной части ЭЦ).

Двухполюсник называется активным, если он содержит хотя бы один источник электрической энергии и напряжение холостого хода на его зажимах не равно нулю, и пассивным в противном случае.

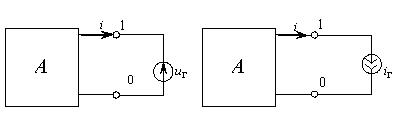
Двухполюсники, обладающие одинаковыми входными характеристиками, называются эквивалентными. На структурных схемах двухполюсники обозначаются прямоугольниками, как показано на рис 4.1.

Если двухполюсник пассивный, то прямоугольник не содержит обозначения “А”.

Для расчета разветвленных ЭЦ можно использовать две теоремы двухполюсников, если интересоваться значением тока и напряжения только одной ветви. Тогда остальную электрическую цепь можно считать некоторым двухполюсником. На рис. 4.1,а) оставшаяся цепь показана активным двухполюсником, а ветвь, которую необходимо рассчитать, представлена некоторым сопротивление R.

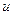
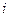
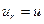
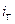
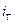
Теорема замещения: значение всех токов и напряжений в цепи не изменится, если любую ветвь цепи с напряжением и током заменить источником напряжения с задающим напряжением или источником тока с задающим током = i. Доказательство теоремы основано на искусственном включении в разрыв ветви между полюсами 1-2-3 двух встречно направленных источников напряжения u₁ и u₂, как показано на рис. 4.1,б), причем u₁ = u₂ = u. В цепи от такого включения ничего не изменится, а часть ветви между полюсами 2 и 0 далее можно убрать, поскольку u₂ = u и направлены встречно друг другу. В результате приходим к схеме рис. 4.2,а), где u_Г = u. По аналогии можно доказать, что рассматриваемую ветвь можно заменить источником тока с задающим током = i (рис. 4.2,б). Доказанная теорема справедлива как для линейных, так и для нелинейных цепей.

Для доказательства второй теоремы необходимо рассмотреть принцип (метод)

наложения (суперпозиции), который справедлив только для линейных цепей.

В основе метода наложения лежит принцип суперпозиции (наложения): напряжения и токи в отдельных ветвях цепи равны алгебраической сумме соответственно напряжений и токов в данных ветвях от каждого напряжения (ЭДС) и тока источников в отдельности. Этот метод применяется в случае, когда в цепи действует несколько источников напряжения или тока. При этом рассчитывают частичные токи и напряжения от каждого из источников, включенных в цепи, а результирующие токи и напряжения определяют путем алгебраического суммирования частичных токов и напряжений. При этом, когда ведется расчет токов и напряжений, вызванных каким-либо одним источником напряжения (ЭДС) или тока, то воздействие остальных источников считается равным нулю, т.е. остальные источники напряжения (ЭДС) в схеме заменяются короткозамкнутыми участками, а ветви с источниками тока размыкаются.

Источник