Как понять что функция симметрична
Четные и нечетные функции
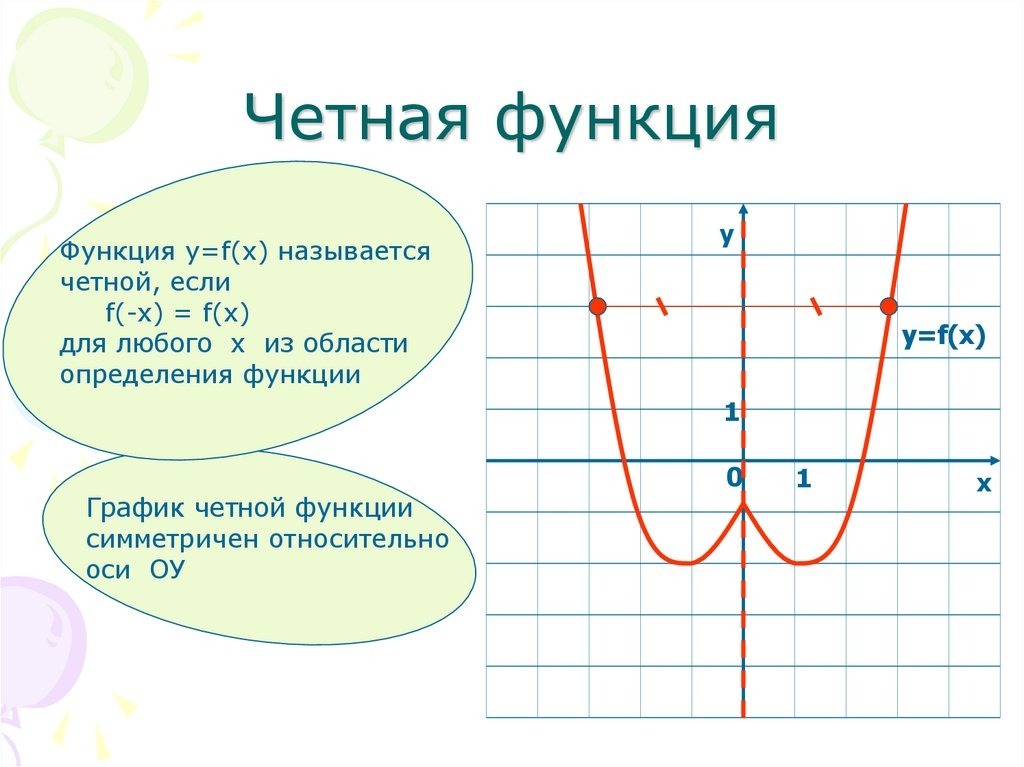
Функция называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График четной функции симметричен относительно оси ординат.
Например, — четные функции.
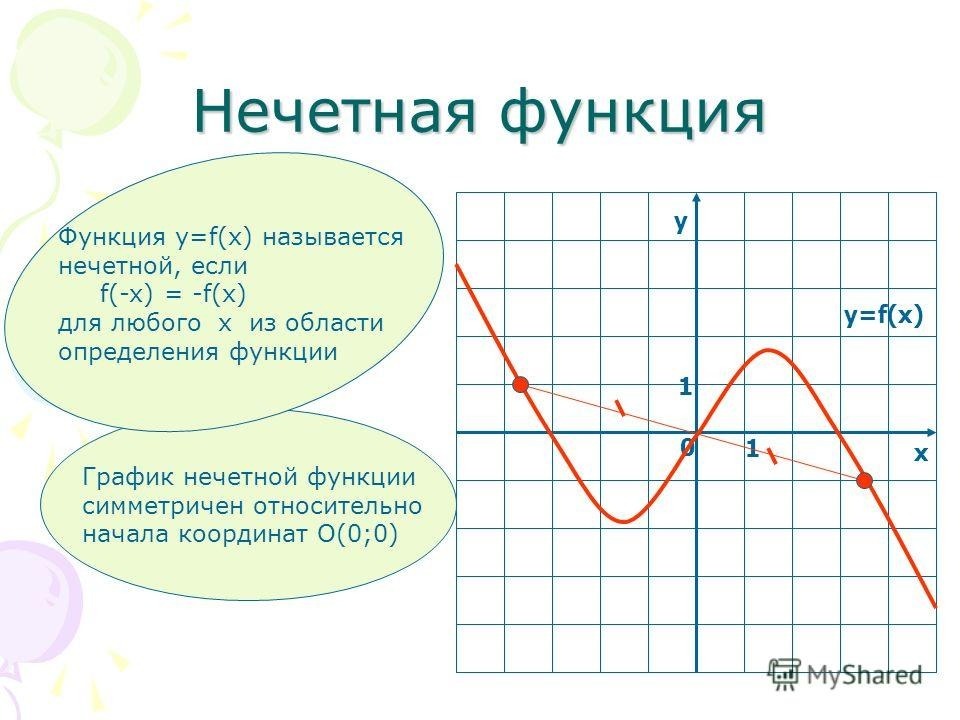
Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.
Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
— значит, функция нечётная, её график симметричен относительно нуля.
2. Проверьте, является ли функция четной (нечетной)
Область определения: все действительные числа.
— чётная, как сумма двух чётных функций.
Её график симметричен относительно оси y.
3. Проверьте, является ли функция четной (нечетной).
Область определения функции симметрична относительно нуля.
— чётная, её график симметричен относительно оси y.
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
№47 Виды симметрии периодических функций.
Различают следующие виды симметрии периодических несинусоидальных функций.
1) Нечетная симметрия: функция симметрична относительно начала координат и удовлетворяет условию f(t)=-f(-t) (рис. 47.1).
Функции, обладающие нечетной симметрией, получили название нечетных. В разложении таких функций содержатся только синусные составляющие отдельных гармоник Bk и отсутствуют постоянная составляющая A0 и косинусные составляющие отдельных гармоник Сk:
При определении коэффициентов ряда Фурье нечетной функции интегрирование в формуле достаточно выполнить за половину периода T/2:
2) Четная симметрия: функция симметрична относительно оси ординат и удовлетворяет условию f(t)=f(-t) (рис. 47.2).
Функции, обладающие четной симметрией, получили название четных. В разложении таких функций содержатся только постоянная составляющая А0 и косинусные составляющие отдельных гармоник Ck и отсутствуют синусные составляющие отдельных гармоник Вк:
При определении коэффициентов ряда Фурье четной функции интегрирование в формулах достаточно выполнить за половину периода:
3) Косая симметрия: функция симметрична относительно оси абсцисс при смещении ее положительной части [f(t)>0] или отрицательной части [f(t)
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Связанное с этим понятие чередующиеся многочлены, которые меняют знак при замене переменных. Помимо полиномиальных функций, тензоры которые действуют как функции нескольких векторов, могут быть симметричными, и фактически пространство симметричных k-тензоры на векторное пространство V является изоморфный в пространство однородные многочлены степени k на В. Симметричные функции не следует путать с четные и нечетные функции, которые обладают другой симметрией.
Содержание
Симметризация
Учитывая любую функцию ж в п переменные со значениями в абелева группа, симметричную функцию можно построить, суммируя значения ж по всем перестановкам аргументов. Точно так же антисимметричная функция может быть построена путем суммирования по даже перестановки и вычитая сумму из нечетные перестановки. Эти операции, конечно, не обратимы и вполне могут привести к функции, которая тождественно равна нулю для нетривиальных функций ж. Единственный общий случай, когда ж может быть восстановлен, если известны его симметризация и антисимметризация, когда п = 2 и абелева группа допускает деление на 2 (обратное удвоению); тогда ж равна половине суммы его симметризации и антисимметризации.
Примеры
Приложения
U-статистика
В статистика, п-выборочная статистика (функция в п переменных), который получается самонастройка симметризация k-выборочная статистика, дающая симметричную функцию в п переменных, называется U-статистика. Примеры включают выборочное среднее и выборочная дисперсия.