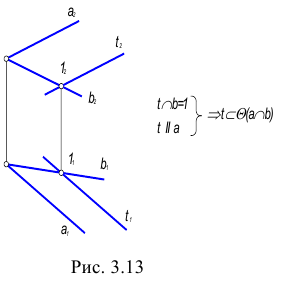
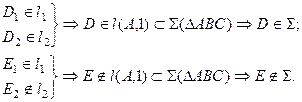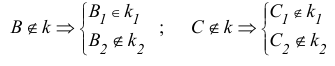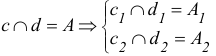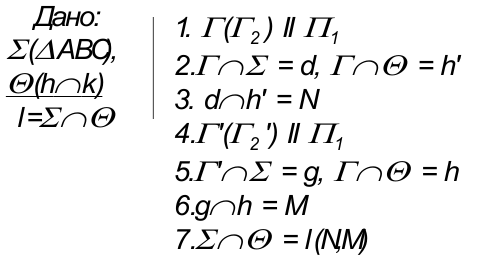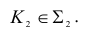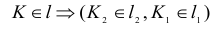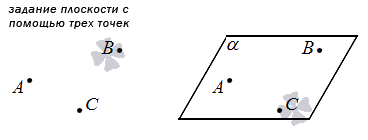Как понять что точка лежит в плоскости
Принадлежность прямой и точки плоскости



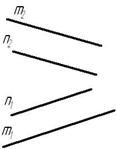
Рис. 3.2 Взаимное расположение прямых
Прямые в пространстве могут занимать относительно друг друга одно из трех положений:
1) быть параллельными;
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
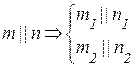
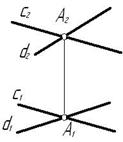
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная (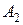
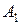
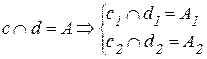
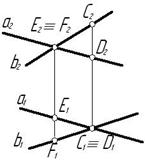
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
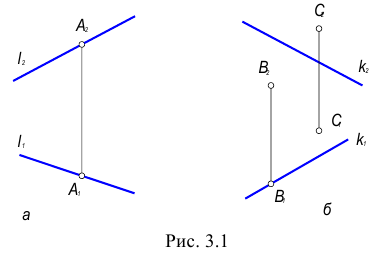
На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.
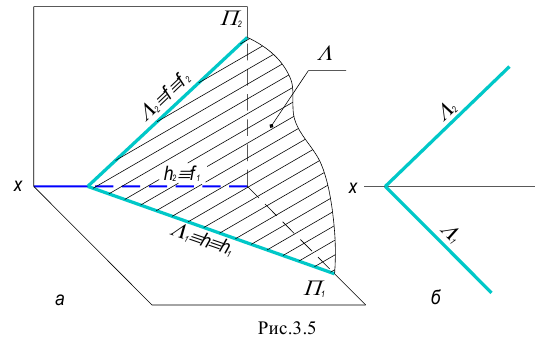
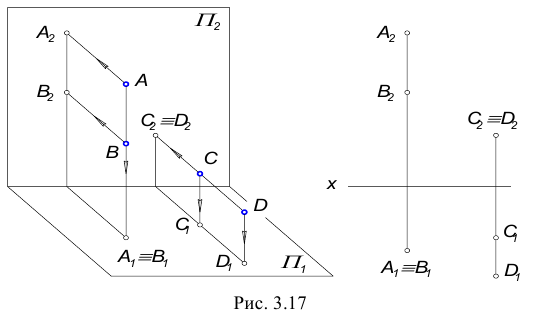
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).
Признак принадлежности точки и прямой плоскости:
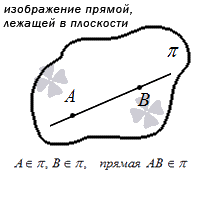
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
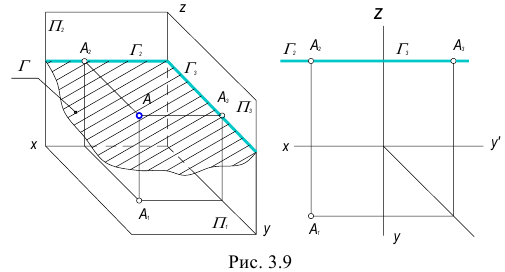
На рис. 3.5 изображена плоскость 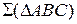
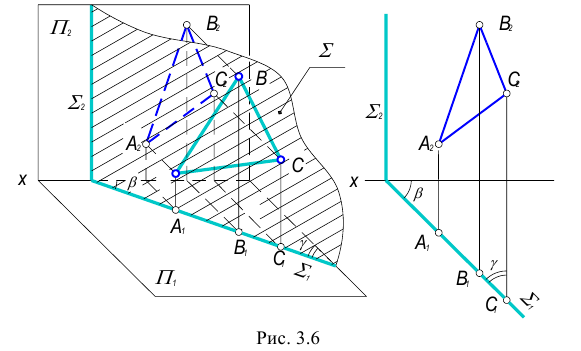
На рис. 3.6 показана плоскость 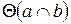
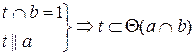
Общее уравнение плоскости : описание, примеры, решение задач
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
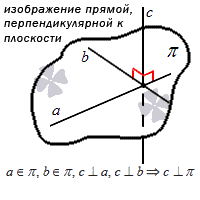
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.
Раскроем чуть шире смысл теорем.
Укажем пример как иллюстрацию этих утверждений.
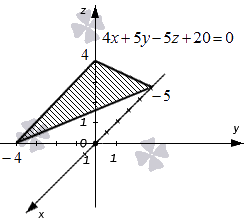
Общее уравнение плоскости, проходящей через точку
Решение
Подставим координаты точки М 0 в исходной уравнение плоскости:
Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.
Решение
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Возможно получить это уравнение другим способом.
Решение
Рассмотрим два способа решения.
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
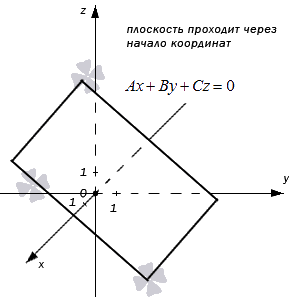
Неполное общее уравнение плоскости
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Решение
Задачу возможно решить еще одним способом.
Решение
Взаимное расположение точки, прямых и плоскостей с примерами
Содержание:
Взаимное расположение точки и прямой:
Возможны два варианта расположения точки относительно прямой:
Взаимное расположение прямых
Прямые в пространстве могут занимать друг к другу одно из трех положений:
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная 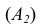
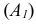
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
На рис. 3.4 точка С принадлежит прямой b, а точка D на прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций.
Плоскость. Способы ее задания, положение относительно плоскостей проекций
Положение плоскости в пространстве может быть однозначно определено:
Всегда от одного способа задания плоскостей можно перейти к другому.
След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.
Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.
Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.
Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.
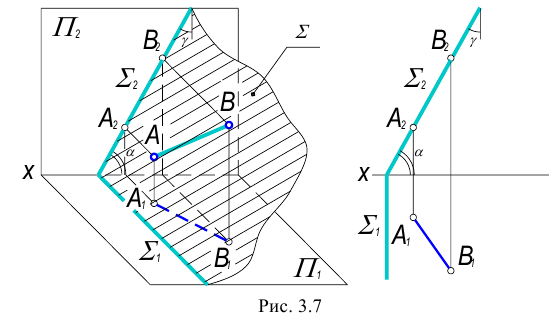
Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.
Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.
2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.
3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
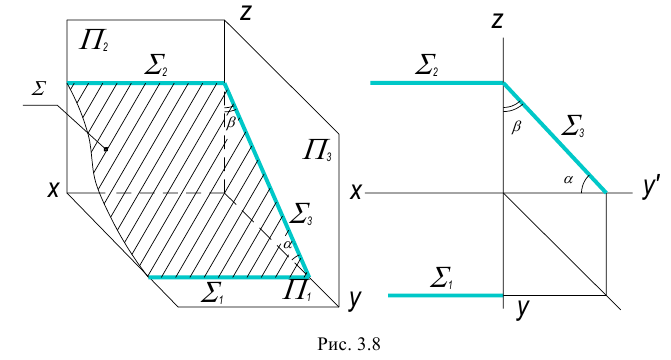
Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.
Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.
1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.
3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.
Принадлежность прямой и точки плоскости
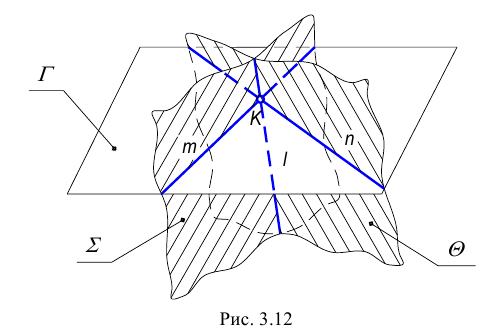
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.12).
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
На рис. 3.12 изображена плоскость 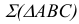
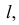
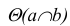
Взаимное расположение прямой и плоскости
Для прямой и плоскости возможны три случая их взаимного расположения:
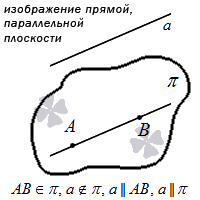
Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.
Этот признак параллельности прямой и плоскости хорошо известен из курса стереометрии.
Взаимное расположение плоскостей
Плоскости по отношению друг к другу могут занимать два положения: быть параллельными или пересекаться.
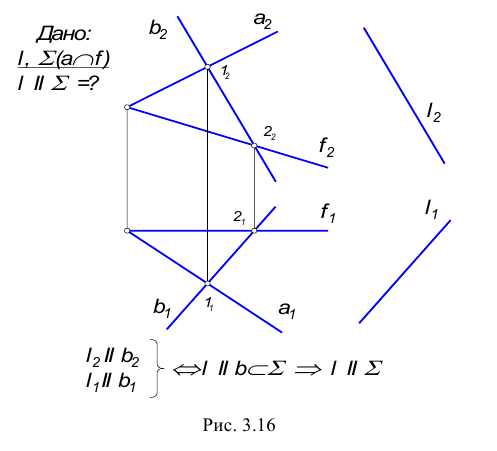
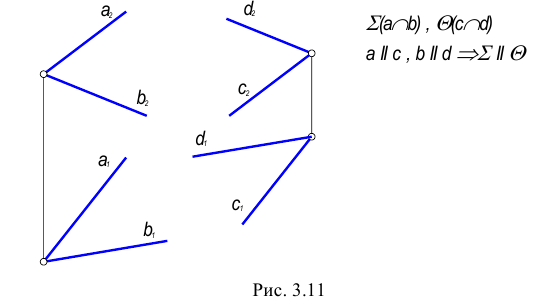
Плоскости параллельны, если пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости
Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая.
Для построения линии пересечения плоскостей необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения.
Направление линии пересечения известно в том случае, если:
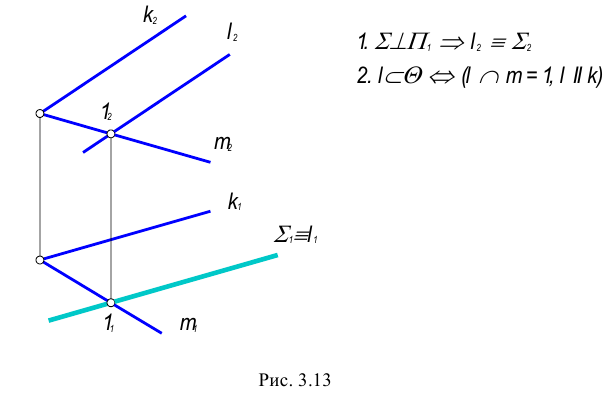
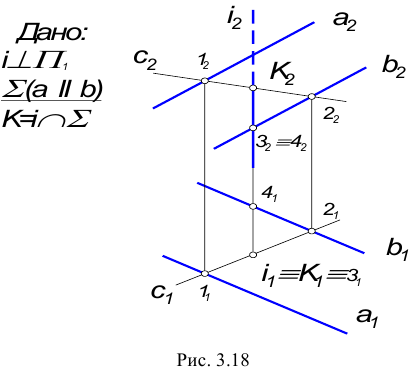
Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 3.12).
Рассмотрим сначала частные случаи пересечение двух плоскостей:
1. Пересекаются плоскость общего положения 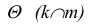
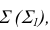
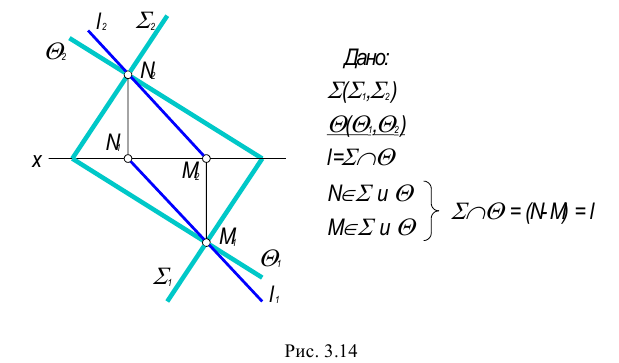
2. Пересекаются плоскости общего положения заданные следами.
В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей.
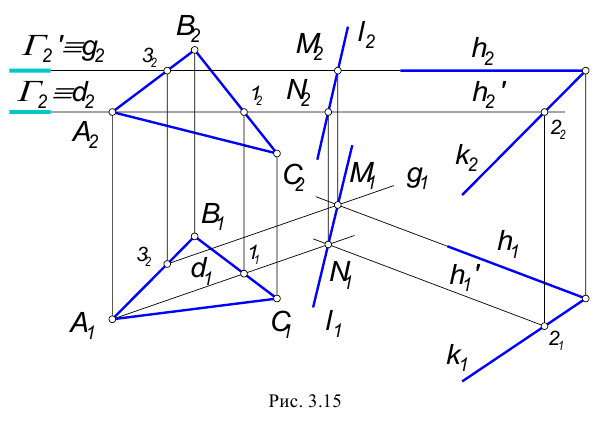
Рассмотрим общий случай пересечения плоскостей:
3. Пересекаются плоскости общего положения.
Определение видимости на КЧ
Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые штриховыми линиями. При этом предполагается, что:
Даны две пары точек:
Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций.
Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой на КЧ находится дальше от оси проекций.
Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – метод конкурирующих точек.
Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам.
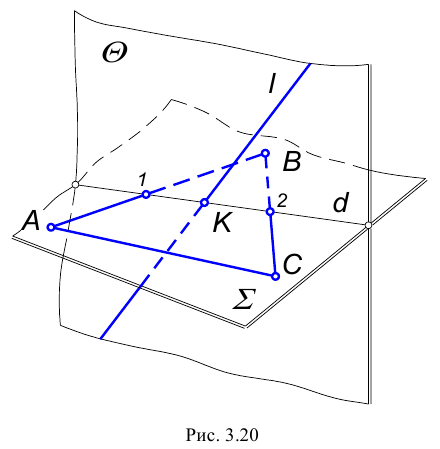
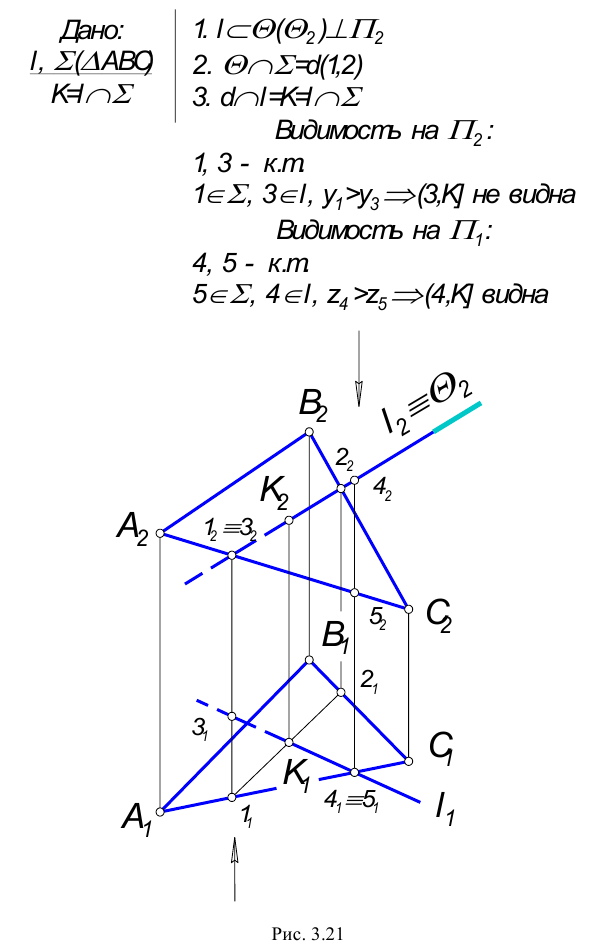
Пересечение прямой с плоскостью
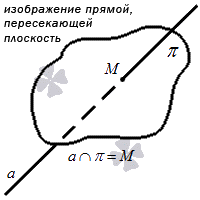
Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости,
1. Прямая – проецирующая, плоскость – частного положения.
На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций. Точка К должна одновременно принадлежать и прямой, и плоскости.
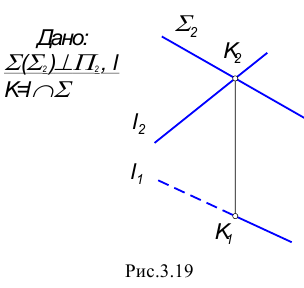
В данном случае фронтальная проекция точки пересечения лежит на следе плоскости
Построение недостающей горизонтальной проекции точки пересечения сводится к задаче на принадлежность точки прямой:
Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).
В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:
Порядок нахождения точки пересечения прямой с плоскостью:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Принадлежность точки и прямой плоскости
Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
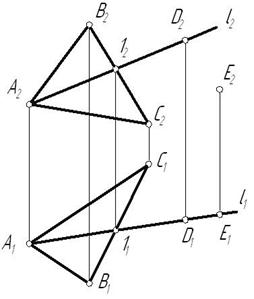
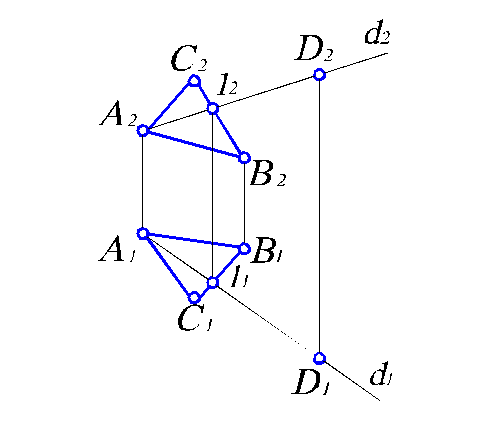
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D1 точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
Через точку D2 проводим проекцию прямой d, лежащей в плоскости DАВС, пересекающую одну из сторон треугольника и точку А2. Тогда точка 12 принадлежит прямым А2D2 и C2В2. Следовательно, можно получить ее горизонтальную проекцию 11 на C1В1 по линии связи. Соединив точки 11 и А1, получаем горизонтальную проекцию d1. Ясно, что точка D1 принадлежит ей и лежит на линии проекционной связи с точкой D2.
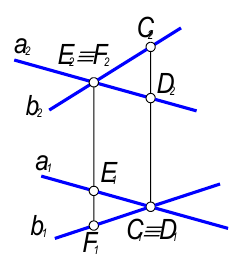
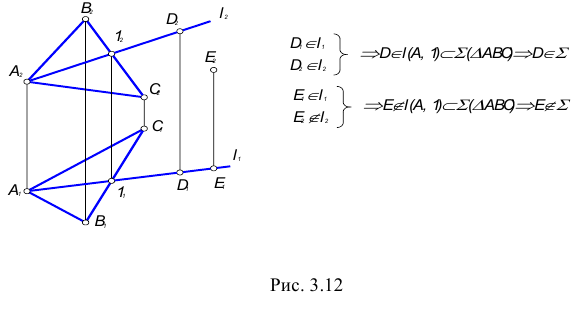
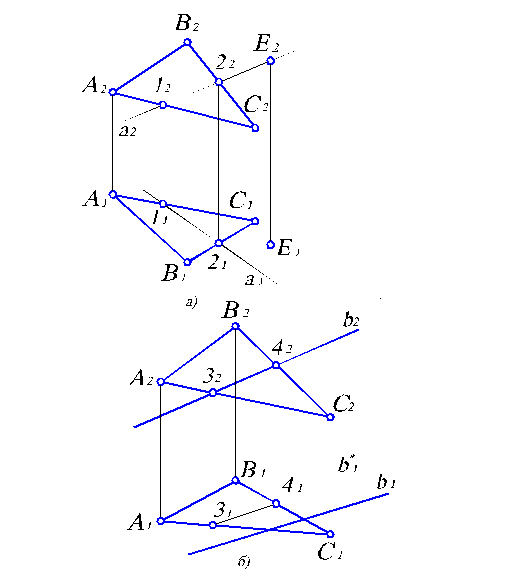
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости DАВС, проведем через ее фронтальную проекцию Е2 прямую а2. Считая, что прямая а принадлежит плоскости DАВС, построим ее горизонтальную проекцию а1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а1 не проходит через точку Е1. Следовательно, точка Е ÏDАВС.
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в2 построить другую в1* считая, что вÌDАВС. Как видим, в1* и в1 не совпадают. Следовательно, прямая в Ë DАВС.
Дата добавления: 2019-10-16 ; просмотров: 627 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
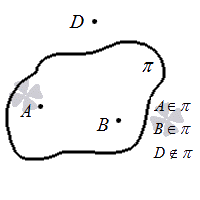
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
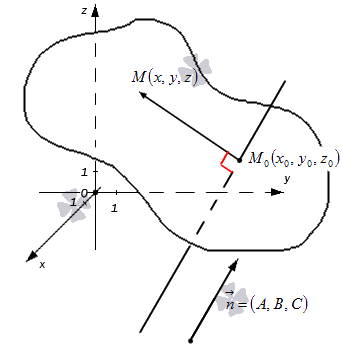
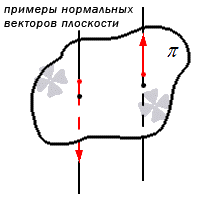
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
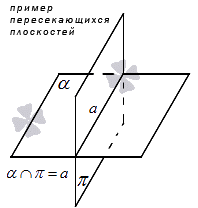
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
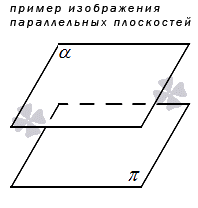
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
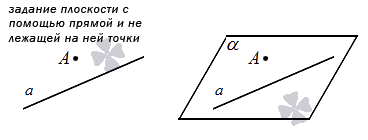
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
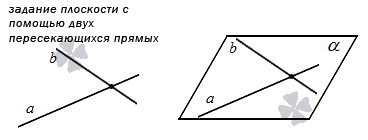
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
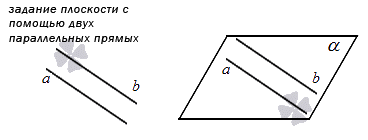
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
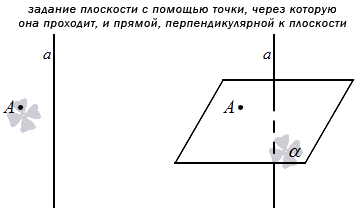
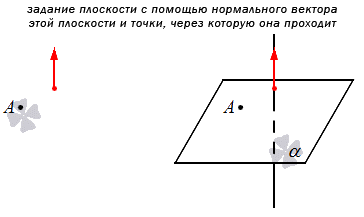
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.