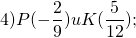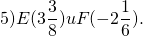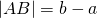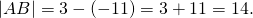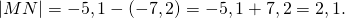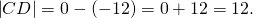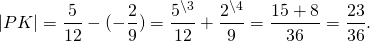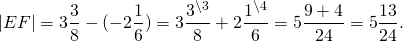Как записать на математическом языке чему равно расстояние между точками
Расстояние между точками на координатной прямой
Расстояние между двумя точками на координатной прямой равно модулю разности их координат.
Формула расстояния между точками на координатной прямой:
где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Пример 1. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.
Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата:
Ответ. Расстояние между точками L и M равно 8.
Пример 2. Найдите координаты середины отрезка AB, если A(-5) и B(5).
Решение. Обозначим середину отрезка точкой C. Так как C — середина отрезка AB, то |AC| = |CB|. Значит, чтобы найти координату точки C, надо сначала вычислить длину отрезка AB и разделить её на 2, то есть, на две равные части AC и CB:
10 : 2 = 5, значит |AC| = |CB| = 5.
Как видно из чертежа, чтобы найти координату середины отрезка, надо половину длины отрезка либо прибавить к точке с наименьшей координатой, либо отнять от точки с наибольшей координатой:
Ответ. Координата середины отрезка C(0).
Пример 3. Найдите координату точки C, которая является серединой отрезка с концами в точках A(7) и B(25).
Ответ. Координата точки C — 16.
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.
Предупреждение
Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
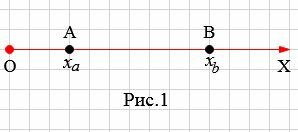 |
Расстояние между точками A и В равно:
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
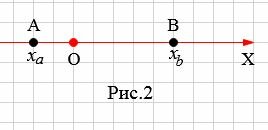 |
На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
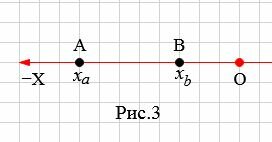 |
B этом случае рассояние между точками A и B равно:
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
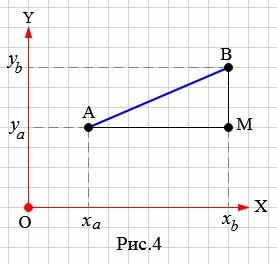 |
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:
Тогда, учитывая (8), получим:
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
 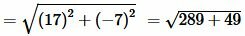 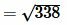 , , |
Ответ: 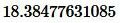
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
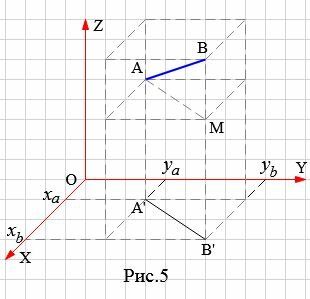 |
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:
Учитывая, что BM равно разности третьих координат точек B и A, получим:
Из предыдующего параграфа следует, что:
Но AM=A’B’. Тогда из (10) и (11) следует:
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
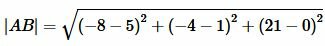 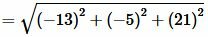 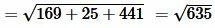 , , |
Ответ: 
Расстояние между точками на координатной прямой
Расстоянием между двумя точками A и B называется длина отрезка, соединяющего эти точки.
Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату левого конца.
Найти расстояние в единичных отрезках между точками:
Чтобы найти расстояние между точками на координатной прямой, определим, какая из точек находится правее, и из координаты правого конца отрезка вычтем координату его левого конца.
Из двух точек на координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.
Для точек A(a) и B(b) это означает, что если b>a, то точка B на координатной прямой лежит правее точки A и расстояние между точками A и B равно
3) Так как 0>-12, точка C (0) на координатной прямой лежит правее точки D(-12). Расстояние между точками C и D:
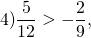
поэтому точка K на координатной прямой расположена правее, чем точка P.
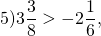
значит, точка E на координатной прямой находится справа от точки F. Поэтому длина отрезка EF, а значит, и расстояние между точками E и F
2 Comments
Для чего находить наибольшее число, если |a-b|=|b-a|?
Дмитрий, всё зависит от учебника. Если данную тему изучают после того, как ввели понятие модуля, то расстояния между точками на координатной прямой можно искать как модуль разности координат этих точек. В противном случае действуем, как описано выше.
Время, скорость, расстояние
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 м
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 м
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Как определить расстояние между двумя точками?
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения. Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе.
Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние от точки до точки: формулы, примеры, решения, формула расстояния между двумя точками
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB). Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек: AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс: AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат: AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее: AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение: AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом: AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
Расстояние между точками на координатной плоскости — формулы и расчеты
Аналитическая геометрия — важная ветвь математики, которая позволяет рассчитать любые характеристики расположения объектов в пространстве, например, углы и дистанции.
Формула расстояния между точками на координатной плоскости является основным инструментом, применяемым при решении ряда задач в двумерном пространстве.
Система координат
Прежде чем говорить о расстоянии между точками по координатам, следует ввести систему отчета, в которой каждый геометрический объект можно будет однозначно определять.
Для этой цели часто используют декартову систему координат. Она представляет собой взаимно перпендикулярные прямые, на каждой из которых отмечены единичные отрезки.
Именно в них определяется положение тел в пространстве, на плоскости или на прямой линии. Для названных трех случаев декартова система координат отличается количеством осей:
Единичные отрезки на координатных осях в общем случае могут иметь разную длину. Однако ввиду симметричности пространства и для удобства выполнения практических расчетов применяют, как правило, единичные отрезки равной длины. Каждому из них соответствует единичный вектор.
Понятие о векторе
Чтобы уметь вычислять расстояние от точки до точки по координатам, удобно пользоваться понятием вектора. Из школьного курса геометрии известно, что под ним принято понимать отрезок, имеющий некоторое определенное направление. Обозначают его в виде прямой линии конечной длины, на конце которой изображена стрелка.
Пользу использования указанного геометрического объекта трудно переоценить. Например, в физике все величины делятся на 2 большие группы:
К первым относятся масса, электрический заряд, энергия и другие. Вторая группа более обширная. Здесь следует назвать скорость, ускорение, силу тока, напряженности магнитного и электрического полей, силу любой природы и многие другие.
Характеристики объекта
Как любой геометрический объект, вектор обладает набором математических свойств, которые используются при решении задач. Основные из них:
Для всех свойств существуют определяющие их правила. Например, при осуществлении вычитания вектора a- из b- необходимо соединить концы этих объектов отрезком и направить его к концу a-, тогда получается результирующий вектор разницы.
Умножение a- и b- векторным способом является полезной операцией при определении площадей и объемов фигур. Для ее выполнения следует уметь работать с матрицами второго и третьего порядка, в частности, знать, как рассчитывается детерминант (определитель).
Универсальный способ
Речь идет о координатном представлении нульмерных, одномерных, двумерных и трехмерных геометрических фигур. Параметры точек, треугольников, квадратов, прямых, плоскостей и других более сложных объектов могут быть однозначно выражены в виде наборов чисел, привязанных к соответствующей координатной системе.
Поскольку существует задача определения расстояния от точки до точки по координатам, имеет смысл рассмотреть только указанный одномерный объект и вектор.
Точка на плоскости
Первое число здесь означает количество единичных отрезков, которые необходимо отсечь на оси x, второе значение — на оси y. Точка D лежит в начале координат, то есть на пересечении x и y. В общем случае удобно обозначить произвольную точку Q (x0; y0).
Направленный отрезок в двумерном пространстве
На плоскости координаты направленного отрезка так же, как и точки, представляют собой набор двух чисел. Оба обозначают число отрезков единичной длины, которые следует отложить на каждой оси, чтобы получить проекции вектора на x и y.
На плоскости и в трехмерном пространстве всего 2 точки однозначно определяют направленный отрезок. Если его начало переместить в пересечение осей x и y, его конец легко можно найти, вычитая соответствующие координаты точек друг из друга. Следующий простой пример демонстрирует сказанное.
Даны точки A (x1; y1), B (x2; y2), тогда AB- будет иметь координаты: AB- = B — A = (x2-x1; y2-y1).
Вторая точка показывает место расположения конца AB-.
Формула дистанции
Имея полученные представления и знания о свойствах точек и векторов, можно перейти к вопросу нахождения формулы расстояния. Согласно геометрическому определению, под дистанцией между двумя точками понимают длину отрезка, который их соединяет. Эта величина также равна модулю вектора, построенного на нульмерных объектах.
Длину направленного отрезка на плоскости определить просто: необходимо возвести в квадрат каждую его координату, сложить полученные значения, и взять квадратный корень из результирующей суммы. Для вектора a- (x; y) длина будет равна следующей величине: |a-| = (x 2 + y 2 )^0,5.
Возведение суммы в степень 0,5 эквивалентно взятию из нее квадратного корня. Поскольку определение координат вектора по соответствующим значениям точек известно, можно получить следующую простую формулу для A (x1; y1) и B (x2; y2): |AB-| = ((x2-x1)^2 + (y2-y1)^2)^0,5.
В трехмерном пространстве соответствующее выражение будет иметь подобную форму, только добавится третья координата z.
Расстояние между Q и прямой
Полученные знания можно с легкостью применять для решения разнообразных задач по геометрии. Часто приходится находить дистанцию между точкой и прямой. Определить эту величину можно, если знать направляющий вектор прямой. Предположим, что он имеет следующие координаты: a- (x1; y1). Прямая проходит через A (x2; y2). Точка задается так: Q (x0; y0).
В параметрическом виде прямая записывается следующим образом: (x;y) = (x2;y2) + t*(x1;y1).
Здесь t — параметр, который может принимать любое действительное число. Это выражение позволяет записать равенство (1): (x-x2)/x1 = (y-y2)/y1 (1).
Пусть точка P (x;y) является проекцией Q (x0;y0) на прямую, тогда расстояние PQ является искомой дистанцией, которую следует найти по условию задачи. Поскольку вектора PQ- и a- перпендикулярны друг другу, их скалярное произведение будет равно нулю (угол между векторами равен 90 градусов, его косинус равен нулю). Исходя из этих рассуждений, можно записать выражение (2): (x-x0)*x1 + (y-y0)*y1 = 0 (2).
Поскольку имеющиеся равенства (1) и (2) содержат 2 неизвестные переменные, объединение их в систему и решение ее позволит определить точку P (x;y). Зная ее координаты и используя формулу дистанции между двумя точками на плоскости, можно получить искомое расстояние PQ.
Пример задачи
Чтобы определить направляющий вектор, достаточно взять 2 любые точки на прямой. Подставляя в выражение произвольные значения x, можно определить эти точки A, B и вместе с ними направляющий вектор AB-:
Вектор QP-, который пересекает прямую под прямым углом, должен подчиняться следующему уравнению (свойство скалярного произведения):
В это выражение нужно подставить значение y из уравнения прямой.
Получается:
Рассчитанное значение округлено до сотых долей и выражается в единицах единичных векторов координатной системы.
При решении подобных задач для сокращения последующих вычислений рекомендуется проверять принадлежность точки прямой, для чего следует подставить координаты в уравнение. Если этот факт подтверждается, искомое расстояние равно нулю.
Углы треугольника
Польза от использования формулы дистанции между точками на плоскости наглядно показывается на примере решения задач на нахождение углов фигур. Пусть нужно определить все углы треугольника, который построен на вершинах A (x1;y1), B (x2;y2), C (x3;y3).
На первый взгляд сложная задача решается легко, если вспомнить о понятии векторного произведения. Например, для векторов AB- и AC- записывается оно так:
Произведение [AB-*AC-] является вектором, который находится как детерминант матрицы третьего порядка. Его модуль, а также длины |AB-| и |AC-| вычисляются по формуле расстояния между двумя точками.
Чтобы определить угол при вершине A треугольника, остается взять функцию арксинуса от отношения векторного произведения к произведению длин сторон AB и AC.