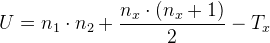Коэффициент манна уитни что показывает
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
U-КРИТЕРИЙ МАННА-УИТНИ
– непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
1. История разработки U-критерия
Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном.
В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.
Хенри Манн
2. Для чего используется U-критерий Манна-Уитни?
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.
3. В каких случаях можно использовать U-критерий Манна-Уитни?
U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.
U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.
Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.
4. Как рассчитать U-критерий Манна-Уитни?
Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.
В составленном едином ранжированном ряду общее количество рангов получится равным:
Наконец, находим значение U-критерия Манна-Уитни по формуле:
5. Как интерпретировать значение U-критерия Манна-Уитни?
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок:
U-критерий Манна-Уитни в дипломной, курсовой и магистерской работе по психологии
Подавляющее большинство психологических исследований направлены на достижение двух главных целей:
В данной статье мы рассмотрим основные аспекты использования критерия Манна-Уитни при обработке результатов эмпирического исследования в курсовых и дипломных работах, а также магистерских диссертациях по психологии.
Зачем нужен критерий Манна-Уитни
В психологическом исследовании изучаются не результаты отдельных испытуемых, а обобщенные данные. Например, при изучении особенностей психологических параметров в двух группах изучаются средние значения в этих группах.
Напомним, что среднее (среднее арифметическое) отражает усредненный по группе показатель. Рассчитывается среднее значение следующим образом:
Таким образом, когда мы сравниваем психологические показатели у двух испытуемых, то никакие статистические критерии не нужны. Действительно, пусть в ходе тестирования уровень личностной тревожности Иванова оказался 40 баллов, а Петрова – 50 баллов. В этом случае мы смело говорим, что Петров более тревожен, чем Иванов. Однако, если речь идет о сравнении двух групп, то ситуация усложняется.
Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. Но как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?
Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.
Для анализа различий средних значений в двух группах используется t-критерий Стъюдента. U-критерий Манна-Уитни позволяет сравнивать не средние значения, а выраженность показателей, но в этом случае и средние значения параметров в группах будут различаться соответствующим образом.
Расчет критерия Манна-Уитни: объяснение простыми словами
В подавляющем большинство психологических исследований расчет статистических критериев в том числе и критерия Манна-Уитни производится с помощью статистических программ. Наиболее известные – это SPSS и STATISTICA. Однако несмотря на это важно в общих чертах представлять себе сущность расчета – это придаст студенту-психологу на защите диплома.
Вернёмся к нашему пример с тревожностью мужчин и женщин. Предположим у нас две группы по 10 человек. У каждого испытуемого есть определенное значение личностной тревожности. Нам нужно выяснить, различаются ли уровни тревожности в группах мужчин и женщин. Расчет критерия Манна-Уитни примерно будет проходить по следующим шагам:
Мы привели объяснение на пальцах. Статистические программы для расчета используют специальные алгоритмы, которые позволяют численно оценить эти пересечения данных обеих групп (синих и красных чисел) и сделать вывод о существовании или не существовании различий.
Что нужно знать про критерий Манна-Уитни на защите диплома
U-критерий Манна-Уитни – это непараметрический статистический критерий, использующийся для сравнения выраженности показателей в двух несвязных выборках.
Что такое непараметрический? Не вдаваясь в статистические тонкости, нужно понимать следующее. Параметрические статистические критерии более точные, но они предъявляют более строгие требования к данным. То есть, перед расчетом нужно все данные в группах проверять, например, на нормальность распределение. Это значит, что на графике распределения такие данные должны располагаться в виде колокола – больше всего испытуемых со средними значениями, а меньшинство имеют низкие и высокие показатели. t-критерий Стъюдента является параметрическим критерием.
Непараметрические критерии менее точные, но зато у них нет жестких требований к данным. Эти данные могут быть почти любыми.
Что значит несвязные выборки? Это означает, что группы не пресекаются, то есть в них разные испытуемые. Расчет различий в связных выборках используется, например, при выявлении эффективности тренингов, когда производятся замеры «до» и «после», а потом сравниваются. У критерия Стъюдента есть вариант для связных выборок. Критерий Манна-Уитни используется только для несвязных.
Ограничения критерия Манна-Уитни
«Почему вы выбрали для расчета критерий Манна-Уитни?»
Очень многих студентов-психологов перед защитой диплома пугает именно этот вопрос. Предлагаем в качестве основы для индивидуальных модификаций следующий ответ:
«В данной работе мы не проверяли данные на нормальность распределения, поэтому мы использовали непараметрический статистический критерий анна-Уитни, предназначенный для выявления различий показателей в двух несвязных выборках».
Важно понимать, что фактически этот вопрос означает следующее: «Почему вы выбрали критерий Манна-Уитни, а не критерий Стъюдента». Именно эти критерии наиболее часто используются для сравнительного анализа в психологических исследованиях.
Поэтому в ответе и надо указать, что на нормальность данные не проверяли, например, из-за небольшого объема групп. Поэтому решили остановиться на непараметрическом критерии.
Уровень статистической значимости
Если вы будет пользоваться для расчета критерия Манна-Уитни статистической программой, то в выдаче результатов будут присутствовать два важных показателя:
Пример анализа данных с помощью критерия Манна-Уитни в дипломе по психологии
Результаты сравнительного анализа показателей жизнестойкости у молодежи и людей зрелого возраста
Автоматический расчет U-критерия Манна-Уитни
U-критерия Манна-Уитни
Инструкция по использованию скрипта (FAQ)
Составлено по материалам книги: Сидоренко Е. В. «Методы математической обработки в психологии». СПб.: ООО «Речь», 2007 г.
Назначение U-критерия Манна-Уитни
Настоящий статистический метод был предложен Фрэнком Вилкоксоном (см. фото) в 1945 году. Однако в 1947 году метод был улучшен и расширен Х. Б. Манном и Д. Р. Уитни, посему U-критерий чаще называют их именами.
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n1,n2≥3 или n1=2, n2≥5, и является более мощным, чем критерий Розенбаума.
Описание U-критерия Манна-Уитни
Существует несколько способов использования критерия и несколько вариантов таблиц критических значений, соответствующих этим способам (Гублер Е. В., 1978; Рунион Р., 1982; Захаров В. П., 1985; McCall R., 1970; Krauth J., 1988).
Чем меньше область перекрещивающихся значений, тем более вероятно, что различия достоверны. Иногда эти различия называют различиями в расположении двух выборок (Welkowitz J. et al., 1982).
Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше Uэмп, тем более вероятно, что различия достоверны.
H0: Уровень признака в группе 2 не ниже уровня признака в группе 1.
H1: Уровень признака в группе 2 ниже уровня признака в группе 1.
Ограничения U-критерия Манна-Уитни
1. В каждой выборке должно быть не менее 3 наблюдений: n1,n2 ≥ З; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; n1, n2 ≤ 60.
Автоматический расчет U-критерия Манна-Уитни
Шаг 1
Введите в первую колонку («Выборка 1») данные первой выборки, а во вторую колонку («Выборка 2») данные второй выборки. Данные вводятся по одному числу на строку; без пробелов, пропусков и т.д. Вводятся только цифры. Дробные числа вводятся со знаком «.» (точка). После заполнения колонок нажмите на кнопку «Шаг 2», чтобы произвести автоматический расчет U-критерия Манна-Уитни.
Книга представляет собой практическое руководство для исследователей, поставивших целью статистически обосновать свои научные и практические выводы. Принцип отбора методов — ясность и простота. Методы рассматриваются на реальных примерах и сопровождаются алгоритмами и графическими иллюстрациями. Все они могут быть использованы для быстрой обработки данных. Руководство предназначено для психологов и специалистов в области социологии, педагогики, медицины, биологии, экономики.
Многие задают вопрос: «Кто я, интроверт или экстраверт?». Я приведу примеры, каким способом те и другие восполняют свою энергию. Прислушайтесь к себе, что вам больше отзывается.
Обычное дело — встречаются два человека, например, мужчина и женщина, желающие знакомства и общения, а поговорить им не о чем. «Неловкое молчание» сковывает их, а мысли о том, что «надо о чем-то разговаривать» усугубляют напряжение и желание «побега».
Основные статистические критерии. Непараметрический критерий Манна-Уитни (U-критерий Манна — Уитни,. Mann–Whitney U-test). Понятие и порядок практического использования
При проведении психологических исследований важно уметь пользоваться не только информацией, но и грамотно ее преобразовывать, интерпретировать и анализировать в целях получения достоверного результата.
При проведении психологических исследований важно уметь пользоваться не только информацией, но и грамотно ее преобразовывать, интерпретировать и анализировать в целях получения достоверного результата.
Одной из распространенных практических методик, позволяющих систематизировать имеющиеся материалы и проанализировать их, является непараметрический критерий манна-Уитни. Этот механизм пришел в психологическую науку из статистики и успешно используется вплоть до настоящего времени.
Зачем необходим критерий Манна-Уитни?
Научно-исследовательский проект по психологии предполагает изучение конкретных объектов с целью установления сходств и различий, особенностей поведения и иных мотивов. Зачастую в качестве объекта научных изысканий выступают отдельные индивиды или целые группы ли, разбитые на несколько групп по определенным признакам. В целях упрощения анализа данных исследователь изучает средние значения конкретных критериев, коэффициентов или «симптомов».
Расчет «среднего» значения производится аналогично среднему арифметическому: суммируют показатели всех испытуемых и делят на количество испытуемых объектов исследования.
Особенность применения критерия Манна-Уитни
Далеко не всегда анализ показателей испытуемых позволяет сделать определенный вывод. Если в исследовании принимает участие всего 2 объекта со схожими параметрами, то получить результат и вывод можно легко. Но если речь идет о группе лиц с разными критериями, то задача усложняется. Решить ее становится возможно при помощи специальной статистической методики «различий». Именно к этому виду относят критерий Манна-Уитни.
Данный механизм позволяет определить степень совпадения или несовпадения в отношении разных выборок, объектов исследования.
Суть непараметрического критерия Манна-Уитни
На сегодняшний день благодаря развитию НТП рассчитывать критерий U-test можно с помощью специальных сервисов: Ststistica, SPSS. Но при написании студенческих и научных работ студенты чаще используют «ручной способ».
Схема применения критерия Манна-Уитни
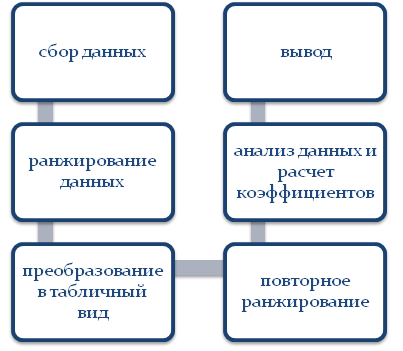
Рассмотрим действие алгоритма на конкретном примере. Допустим, исследователь намерен оценить уровень обеспокоенности (взволнованности, тревожности) у разнополых объектов. В каждой группе будет принимать участие по 10 человек. У каждого индивида зафиксирован определенный уровень обеспокоенности, который был оценен по 10-балльной шкале. Исследователю важно определить, сильно ли отличается значение исследуемого параметра мужчин и женщин. Для этого достаточно следовать по этапам:
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Использование специальных программ для расчета критерия Манна-Уитни позволяет в считанные минуты провести численный анализ и представить результаты в виде графиков, где будет очевидно пересечение или не пересечение исследуемых групп. Программа укажет два важных параметра:
В ходе использования непараметрического критерия U-test важно учесть определенные ограничения: количество испытуемых лиц не должно превосходить 60, минимальное количество объектов исследования – 3. Выборка может быть равномерной или неравномерной. Сравнивать можно самые разные показатели (психологические и непсихологические), главное располагать нужными данными.
Пример использования критерия Манна-Уитни в психологическом исследовании
Команда Дисхелп готова выполнить студенческую или научно-исследовательскую работу по психологии. Наши специалисты помогут в формировании информационной базы проекта, проведении эксперимента и анализа полученных данных. У нас работают преподаватели ведущих ВУЗов, кандидаты и доктора наук, практикующие эксперты. Мы гарантируем соблюдение дедлайнов и всех заявленных заказчиком требований. Высокое качество, конфиденциальность данных и индивидуальный подход – всегда в нашем арсенале. Убедитесь в этом лично, оформив заявку на нашем сайте.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
Критерий Уилкоксона-Манна-Уитни
Материал из MachineLearning.
U-критерий Манна-Уитни (Mann-Whitney U test) — непараметрический статистический критерий, используемый для оценки различий между двумя выборками по признаку, измеренному в количественной или порядковой шкале. U-критерий является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения.
Другие названия: критерий Манна-Уитни-Уилкоксона (Mann-Whitney-Wilcoxon, MWW), критерий суммы рангов Уилкоксона (Wilcoxon rank-sum test) или критерий Уилкоксона-Манна-Уитни (Wilcoxon-Mann-Whitney test, WMW).
Содержание
Примеры задач
Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.
Пример 2. Первая выборка — это поля, обработанные агротехническим методом А. Вторая выборка — поля, обработанные агротехническим методом Б. Значения в выборках — это урожайность. Требуется выяснить, является ли один из методов эффективнее другого, или различия урожайности обусловлены случайными факторами.
Пример 3. Первая выборка — это дни, когда в супермаркете проходила промо-акция типа А (красные ценники со скидкой). Вторая выборка — дни промо-акции типа Б (каждая пятая пачка бесплатно). Значения в выборках — это показатель эффективности промо-акции (объём продаж, либо выручка в рублях). Требуется выяснить, какой из типов промо-акции более эффективен.
Описание критерия
Замечание: менее рациональный способ вычисления статистик Манна-Уитни :
y_j\right].» alt= «U_y = \sum_
Асимптотический критерий: нормированная и центрированная статистика Манна-Уитни
асимптотически имеет стандартное нормальное распределение при 8″ alt= «m,\,n > 8» />.
Свойства и границы применимости U-критерия
Иногда ошибочно считают, что U-критерий проверяет нулевую гипотезу равенства медиан в двух выборках. Существуют распределения, для которых гипотеза верна, но их медианы различны.
U-критерий является непараметрическим аналогом критерия Стьюдента. Если выборки нормальные, то для проверки гипотезы сдвига предпочтительно применить более мощный критерий Стьюдента.
История
Данный метод выявления различий между выборками был предложен в 1945 году Френком Уилкоксоном. В 1947 году он был существенно переработан и расширен Манном и Уитни, по именам которых сегодня обычно и называется.