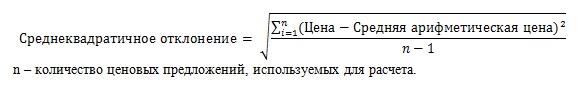Коэффициент вариации для чего

Расчет коэффициента вариации

Понятие коэффициента вариации

В статистике под вариацией величин того или иного показателя в совокупности понимается различие его уровней у тех или иных единиц анализируемого состава в один и тот же период либо момент исследования. В том случае, когда выполняется анализ отличий величин показателя у одного и того же предмета, у одной и той же единицы совокупности в различные периоды или моменты времени, то это будет уже именоваться не вариацией, а колебаниями или изменениями в течении определенного периода.

Размещено на www.rnz.ru

Формула расчета коэффициента вариации

Являясь отношением среднего квадратического отклонения к средней величине, в общем случае анализируемый показатель вычисляется по следующей формуле:

Формула расчета коэффициента вариации

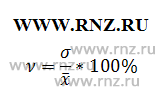
Вычисление рассматриваемого показателя посредством расчета отклонений от средней величины отражает его объективное содержание, но его получение достаточно трудоемко, и для повышения точности выводов требуются расчеты среднего показателя и отклонений без округлений или со значительным количеством цифр после запятой. Поэтому в практических вычислениях делимое может быть вычислено с использованием другой, полученной из общей, формуле вычисления среднего квадратического отклонения в форме разности среднего квадрата элемента и квадрата среднего значения. Таким образом, формула расчета исследуемого показателя, дающая более точный результат, выглядит следующим образом:

Формула расчета точного значения коэффициента вариации

Пример расчета коэффициента вариации

Приведем пример расчета коэффициента вариации цены. Исходные данные для вычисления коэффициента вариации и необходимые промежуточные расчеты приведены в таблице:

Для вычисления используем следующую формулу:

Определим средне значение: х_{среднее} = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.

Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.

Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.

Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.

Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ

Онлайн калькулятор расчета коэффициента вариации

В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.

Онлайн-калькулятор расчета коэффициента вариации:

Источник

Коэффициент вариации по 44-ФЗ. Пример расчёта, формула

Одной из ключевых стадий подготовки закупочной документации становится расчет начальной максимальной цены контракта (НМЦК). Законодательно предусмотрено несколько способов, с помощью которых можно производить расчеты. Чаще всего используется метод сопоставимых рыночных цен. При этом итоговая НМЦК должна определяться с учетом коэффициента вариации. Поэтому всем заказчикам необходимо понять, что включает в себя этот показатель и как его правильно определить.

Что такое коэффициент вариации

Размер НМЦК определяется еще на этапе планирования. Эта сумма должна быть отражена в плане и план-графике. Непосредственно перед подготовкой извещения она корректируется с учетом сложившейся на тот момент экономической обстановки. Вопросы, связанные с НМЦК рассматриваются в статье 22 44-ФЗ. Методики ее расчета описаны в Приказе Министерства экономики и развития № 567 от 02 октября 2013 года. В этом же документе приводятся правила определения коэффициента вариации.

Разработано несколько методик выявления НМЦК: нормативная, тарифная, проектно-сметная, затратная. Самым приоритетным считается метод сопоставимых рыночных цен. Именно его рекомендуется использовать при определении стартовой цены. Он предполагает сравнение коммерческих предложений, предоставляемых потенциальными поставщиками по запросу заказчика. Для проведения такого анализа и применяется коэффициент вариации. Он выражается в процентах.

Под коэффициентом вариации понимается мера относительного разброса предлагаемых цен. Он показывает, какую долю занимает средний разброс цен от среднего значения цены. Этот показатель может принимать следующие значения:

Для определения коэффициента разработана специальная формула. По ней легко подсчитать параметр, подставив соответствующие данные. Упростить себе задачу можно, используя калькуляторы, которые сегодня широко представлены в интернете.

Что делать, если коэффициент завышен

Если при расчете коэффициента вариации получилось значение меньше 33%, то выборка признается однородной. Следовательно, полученное значение можно использовать для определения НМЦК.

Если возникла такая ситуация, что значение коэффициента оказывается выше 33 процентов, тогда потребуется внесение корректировок в используемые данные. Для этого проводится дополнительное исследование рынка. Необходимо собрать коммерческие предложения от большего количества поставщиков и повторить расчет на основе новых данных. Если собрать дополнительные предложения не получается, можно воспользоваться сведениями из ранее заключенных договоров, которые хранятся в реестре контрактов.

В крайней ситуации, когда никак не получается добиться нужного коэффициента вариации можно исключить из выборки неподходящие предложения. Вы также можете попросить поставщика указать в своем предложении нужную вам сумму.

Правила расчета

Методика расчета коэффициента вариации прописана в приказе Минэкономразвития № 567. Согласно действующим нормам заказчик должен направить не менее пяти запросов коммерческих предложений потенциальным поставщикам. Для расчета используются не менее трех предложений, полностью соответствующих требованиям заказчика.

Стоит отметить, что приказ № 567 не является нормативным актом, следовательно, его исполнение не обязательно. За его нарушение никаких штрафных санкций не предусматривается. Однако во избежание спорных ситуаций заказчика рекомендуется пользоваться именно этими правилами расчета.

Для определения коэффициента вариации применяется следующая формула:

Среднеквадратичное отклонение позволяет определить разброс данных. Для его определения выбирают среднюю цену и меру разброса. Вычислить среднеквадратичное отклонение удается по следующей формуле:

В ситуациях, когда закупка включает в себя одновременно несколько позиций, расчет ведется по каждой из них. Это позволяет выявить товары с наибольшим разбросом цен.

Пример расчета

Предположим, что государственное учреждение проводит закупку принтеров для собственных нужд. Потенциальным поставщикам были отправлены соответствующие запросы. Было получено четыре коммерческих предложения цен: 2500 рублей, 2800 рублей, 2450 рублей и 2600 рублей.

В первую очередь необходимо рассчитать среднеарифметическое значение цены

Следующим шагом становится расчет среднеквадратичного отклонения

Осталось только рассчитать коэффициент вариации

Полученное значение коэффициента меньше 33%, следовательно, все собранные данные подходят для расчета стартовой цены контракта. Расчет НМЦК и коэффициента вариации оформляются в форме отчета, который становится обязательной частью закупочной документации.

Коэффициент вариации – важный инструмент, позволяющий оценить правильность ценовых предложений, полученных от поставщиков. Поэтому при составлении документации заказчикам необходимо учитывать правила расчета этого показателя и особенности его применения.

Источник

Коэффициент вариации (CV)

Коэффициент вариации (coefficient of variation, CV) — это статистическая мера дисперсии (разброса) данных вокруг некоторого среднего значения. Коэффициент вариации представляет собой отношение среднеквадратичного отклонения к среднему значению и является весьма полезной величиной для сравнения степени вариации при переходе от одного ряда данных к другому, даже если их средние значения резко отличаются друг от друга.

Понимание коэффициента вариации

Коэффициент вариации показывает степень изменчивости некоторой выборки данных по отношению к среднему их значению. В финансах данный коэффициент позволяет инвесторам определить, насколько велика волатильность, или риск, по сравнению с величиной ожидаемой прибыли от инвестиций.

Чем меньше значение CV, тем лучший компромисс наблюдается между риском и доходностью. Обратите внимание, что если ожидаемая доходность в знаменателе отрицательна или равна нулю, полученное значение коэффициента может ввести вас в заблуждение.

Коэффициент вариации может быть весьма полезен при использовании соотношения риск/прибыль для выбора объекта инвестиций. Например, инвестор не склонный к риску будет рассматривать активы с исторически низкой степенью волатильности и высокой степенью доходности по отношению к общему рынку (или к отдельной отрасли). И наоборот, инвесторы склонные к риску, будут стремиться инвестировать в активы с исторически высокой степенью волатильности.

Формула CV может использоваться для определения дисперсии между исторической средней ценой и текущими показателями цены акции, товара или облигации.

Обычно данный коэффициент используют в таких целях как:

КЛЮЧЕВЫЕ МОМЕНТЫ

Формула CV

Ниже приведена формула для расчета коэффициента вариации:

Обратите внимание, что если значение ожидаемой доходности в знаменателе формулы коэффициента вариации отрицательна или равна нулю, то результат расчёта по ней нельзя считать корректным.

Коэффициент вариации в Excel и Open Office

Коэффициент вариации можно достаточно легко рассчитать в Excel. Несмотря на то, что в нём нет стандартной функции для расчёта CV, но зато есть функции позволяющие рассчитать стандартное отклонение (СТАНДОТКЛОН) и среднее значение (СРЗНАЧ). Сначала используйте функцию стандартного отклонения, затем вычислите среднее значение, а после этого разделите ячейку, содержащую стандартное отклонение, на ячейку содержащую среднее значение.

В Open Office данный показатель рассчитывается аналогично. Функция стандартного отклонения здесь — STDEV, а функция среднего значения — AVERAGE.

Давайте рассмотрим пример расчёта коэффициента вариации в Open Office. Предположим, что у нас есть три потенциальных объекта для инвестиций — объект А, объект Б и объект В. Прибыль по каждому из этих проектов за последние 6 лет занесена в таблицу представленную ниже:

Давайте рассчитаем значение CV для каждого из этих объектов. Начнём с расчёта стандартных отклонений. Для этого применим к ряду значений прибыли отдельно по каждому объекту функцию STDEV:

Аналогичным образом рассчитаем среднее значение для каждого ряда данных:

Наконец рассчитаем CV. Для этого разделим полученные значения отклонений на средние значения. В результате получим следующую таблицу:

Кликните по картинке для увеличения

Очевидно, что из всех представленных объектов инвестиций предпочтительным будет объект Б имеющий наименьшее значение коэффициента CV.

Пример использования коэффициента вариации для выбора объекта инвестиций

Рассмотрим инвестора не склонного к риску, который хочет инвестировать в биржевой фонд (ETF) состоящий из корзины ценных бумаг отслеживающей индекс широкого рынка. Инвестор выбирает SPDR S&P 500 ETF, Invesco QQQ ETF и iShares Russell 2000 ETF. Затем он анализирует доходность и волатильность выбранных ETF за последние 15 лет и предполагает, что в будущем они могут иметь аналогичную доходность в отношении к своим долгосрочным средним значениям.

Для принятия решения инвестором используется следующая 15-летняя историческая информация:

Исходя из этих данных, инвестор может инвестировать либо в SPDR S&P 500 ETF, либо в iShares Russell 2000 ETF, так как соотношение риска и вознаграждения для них является сравнительно одинаковым. А для Invesco QQQ ETF соотношение риск-доходность, как видите, будет несколько хуже.

Источник

Тема 9 Показатели вариации

Показатели вариации в анализе взаимосвязей

Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.

Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Осо­бое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

Основными показателями, характеризующими вариацию, являются:

1) Размах вариации

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:

где –абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.

3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:

5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:

Таблица 9.1 ‑ Данные о продаже основных марок холодильников:

Рассчитаем размах вариации.

R= 1200-460=740$

Пример вычисления размаха вариации

Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.

Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.

Между индиви­дуальными отклонениями от средней и колеблемостью признака существует прямая зави­симость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.

Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной

По приведенным выше данным определим средневзвешенную цену холодильника:

Далее рассчитаем дисперсию:

. Следует отметить, что дисперсия еще не дает представления об однородности со­вокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рас­считан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, на­сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .

Рассчитаем среднее квадратическое отклонение

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости ка­кого-либо одного признака или для определения однородности совокупности рассчиты­вают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации, среднего линейно­го отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.

Определим значение показателя вариации по вышеприведенным данным таблицы

Совокупность считается однородной, если V не превышает 33%.

Если V 25% – вариация сильная.

Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

!! Следует отметить, что коэффициент вариации может быть более 100%, что, в част­ности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Изучая вариацию интересующего нас признака в пределах исследуемой совокупно­сти и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подвер­женным влиянию).

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации резуль­тативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индиви­дуальных значений признака, используют правило сложения дисперсий.

Общая дисперсия представляет собой сумму средней из виутригрупповой и меж­групповой и дисперсий:

Общая дисперсия характеризует вариацию признака по всей совокупности как ре­зультат влияния всех факторов, определяющих индивидуальные различия единиц сово­купности.

Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результа­тивного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рас­считывается отдельно по каждой j-ой группе.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении об­щей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчле­нения общей совокупности.

Теснота связи между факторным и результативным признаками оценивается на ос­нове эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Пример. На следующем условном примере исследуем зависимость объема выполненных ра­бот от формы собственности проектно-изыскательских организаций.

Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности

Объем выполненных работ

Форма собственности	Количество предприятий	Итого
Государственная	4	10,30,20,40	100
Негосударственная	6	20, 40, 60, 20, 50, 50	240
Итого	10	340

1) Определим средний объем работ для предприятий двух форм собственности.

2) Определим средний объем работ для каждой формы собственности.

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.

Таблица 9.3. – Вспомогательная таблица

Государственная425125Негосударственная640233Итого10

Пример. Средняя из внутригрупповых дисперсий

Пример. Межгрупповая дисперсия

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

Проверка закона сложения дисперсий: 54,0+189,8=243,8

Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фак­тора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.

Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика

Контрольные задания

Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.

2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.

Источник