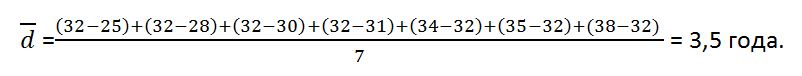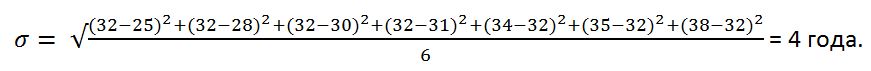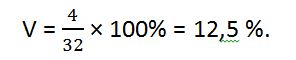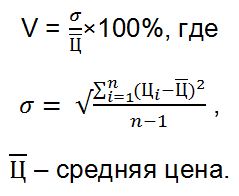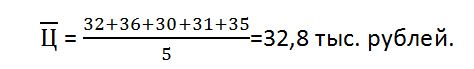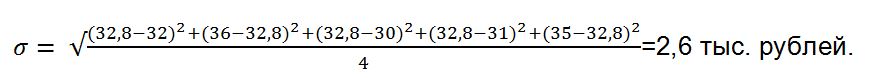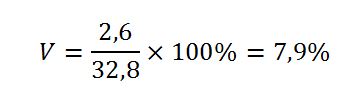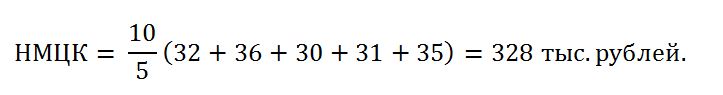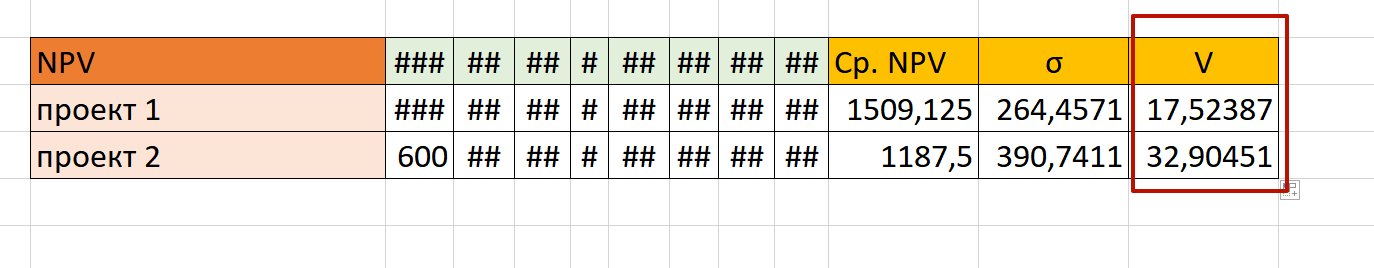Коэффициент вариации составляет 0 3 это означает что

Коэффициент вариации: для чего нужен, расчет, примеры, упражнения

Содержание:

В коэффициент вариации (CV) выражает стандартное отклонение относительно среднего. То есть он пытается объяснить, насколько велико значение стандартного отклонения по отношению к среднему.

Например, переменный рост четвероклассников имеет коэффициент вариации 12%, что означает, что стандартное отклонение составляет 12% от среднего значения.

Обозначается CV, коэффициент вариации является безразмерным и получается делением стандартного отклонения на среднее значение и умножением на сто.

Чем меньше коэффициент вариации, тем меньше отклонение данных от среднего. Например, в переменной со средним значением 10 и другой со средним значением 25, обе со стандартным отклонением 5, их коэффициенты вариации составляют 50% и 20% соответственно. Конечно, первая переменная более изменчива (дисперсия), чем вторая.

Рекомендуется работать с коэффициентом вариации для переменных, измеряемых в шкале пропорций, то есть шкалах с абсолютным нулем независимо от единицы измерения. Примером может служить переменная расстояния, которая не имеет значения, измеряется она в ярдах или метрах, ноль ярдов или ноль метров означает одно и то же: нулевое расстояние или смещение.

Для чего нужен коэффициент вариации?

Коэффициент вариации служит для:

— Коэффициент вариации часто используется как показатель надежности в научных экспериментах. Говорят, что если коэффициент вариации составляет 30% или больше, результаты эксперимента следует отбросить из-за их низкой надежности.

— Это позволяет предсказать, насколько сгруппированы вокруг среднего значения изучаемой переменной, даже не зная ее распределения. Это очень помогает при оценке ошибок и вычислении размеров выборки.

Предположим, что переменные вес и рост людей измеряются в совокупности. Вес с CV 5% и рост с CV 14%. Если вы хотите взять выборку из этой совокупности, размер выборки должен быть больше для оценок роста, чем для веса, поскольку существует большая вариативность в измерении роста, чем в измерении веса.

Важное наблюдение за полезностью коэффициента вариации заключается в том, что он теряет смысл, когда значение среднего близко к нулю. Среднее значение является делителем вычисления CV, и, следовательно, очень маленькие его значения приводят к тому, что значения CV будут очень большими и, возможно, не поддающимися вычислению.

Как рассчитывается?

Расчет коэффициента вариации относительно прост, достаточно знать среднее арифметическое и стандартное отклонение набора данных, чтобы рассчитать его по формуле:

Если они неизвестны, но данные доступны, можно предварительно рассчитать среднее арифметическое и стандартное отклонение, используя следующие формулы:

Примеры

Пример 1

Были измерены веса в кг группы из 6 человек: 45, 62, 38, 55, 48, 52. Мы хотим знать коэффициент вариации переменной веса.

Он начинается с вычисления среднего арифметического и стандартного отклонения:

Ответ: коэффициент вариации переменного веса 6 человек в выборке составляет 16,64%, при среднем весе 50 кг и стандартном отклонении 8,32 кг.

Пример 2

В отделении неотложной помощи больницы измеряют температуру тела в градусах Цельсия у 5 детей, находящихся на лечении. Результаты 39-е, 38-е, 40-е, 38-е и 40-е. Какой коэффициент вариации переменной температуры?

Он начинается с вычисления среднего арифметического и стандартного отклонения:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной для 5 детей в выборке составляет 2,56%, при средней температуре 39 ° C и стандартном отклонении 1 ° C.

Что касается температуры, то следует проявлять осторожность при обращении с весами, поскольку, будучи переменной, измеряемой в интервальной шкале, она не имеет абсолютного нуля. В рассматриваемом случае, что бы произошло, если бы температуры были преобразованы из градусов Цельсия в градусы Фаренгейта:

Рассчитываются среднее арифметическое и стандартное отклонение:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации температурной переменной у 5 детей в выборке составляет 1,76%, при средней температуре 102,2 ° F и стандартном отклонении 1,80 ° F.

Решенные упражнения

Упражнение 1

Вес в кг 10 сотрудников почтового отделения был измерен: 85, 62, 88, 55, 98, 52, 75, 70, 76, 77. Мы хотим знать коэффициент вариации переменной веса.

Рассчитываются среднее арифметическое и стандартное отклонение:

Теперь он подставляется в формулу для коэффициента вариации:

Ответ: коэффициент вариации переменного веса 10 человек в почтовом отделении составляет 19,74%, при среднем весе 73,80 кг и стандартном отклонении 14,57 кг.

Упражнение 2.

В одном городе измеряется рост 9 465 детей во всех школах первого класса, средний рост составляет 109,90 см со стандартным отклонением 13,59 см. Рассчитайте коэффициент вариации.

Ответ: коэффициент вариации переменного роста первоклассников города составляет 12,37%.

Упражнение 3.

Смотритель парка подозревает, что популяции черных и белых кроликов в его парке не имеют одинаковой изменчивости в размерах. Чтобы продемонстрировать это, он взял образцы по 25 кроликов из каждой популяции и получил следующие результаты:

— Белые кролики: средний вес 7,65 кг и стандартное отклонение 2,55 кг.
-Черные кролики: средний вес 6,00 кг и стандартное отклонение 2,43 кг.

Смотритель парка прав? Ответ на гипотезу смотрителя парка можно получить с помощью коэффициента вариации:

Ответ: коэффициент вариации веса черных кроликов почти на 7% больше, чем у белых кроликов, поэтому можно сказать, что смотритель парка прав в своем подозрении, что вариабельность веса двух популяций кроликов не равны.

Ссылки

37 животных в Чили под угрозой исчезновения

18 продуктов, богатых витамином К (натуральный)

Источник

Расчет коэффициента вариации

Понятие коэффициента вариации

В статистике под вариацией величин того или иного показателя в совокупности понимается различие его уровней у тех или иных единиц анализируемого состава в один и тот же период либо момент исследования. В том случае, когда выполняется анализ отличий величин показателя у одного и того же предмета, у одной и той же единицы совокупности в различные периоды или моменты времени, то это будет уже именоваться не вариацией, а колебаниями или изменениями в течении определенного периода.

Размещено на www.rnz.ru

Формула расчета коэффициента вариации

Являясь отношением среднего квадратического отклонения к средней величине, в общем случае анализируемый показатель вычисляется по следующей формуле:

Формула расчета коэффициента вариации

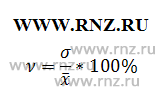
Вычисление рассматриваемого показателя посредством расчета отклонений от средней величины отражает его объективное содержание, но его получение достаточно трудоемко, и для повышения точности выводов требуются расчеты среднего показателя и отклонений без округлений или со значительным количеством цифр после запятой. Поэтому в практических вычислениях делимое может быть вычислено с использованием другой, полученной из общей, формуле вычисления среднего квадратического отклонения в форме разности среднего квадрата элемента и квадрата среднего значения. Таким образом, формула расчета исследуемого показателя, дающая более точный результат, выглядит следующим образом:

Формула расчета точного значения коэффициента вариации

Пример расчета коэффициента вариации

Приведем пример расчета коэффициента вариации цены. Исходные данные для вычисления коэффициента вариации и необходимые промежуточные расчеты приведены в таблице:

Для вычисления используем следующую формулу:

Определим средне значение: х_{среднее} = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.

Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.

Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.

Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.

Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ

Онлайн калькулятор расчета коэффициента вариации

В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.

Онлайн-калькулятор расчета коэффициента вариации:

Источник

Тестовые задания с ответами. 1. Коэффициент вариации составляет 0,3:

1. Коэффициент вариации составляет 0,3:

а) это означает, что риск высокий,

б) это означает, что риск актива средний,

в) это означает, что степень риска низкая,

г) это означает, что риск равен нулю.

2. В управлении рисками используют следующие подходы:

г) верного ответа нет.

3. Ковариация имеет отрицательное значение, если:

а) доходности активов, входящих в портфель, изменяются однонаправлено,

б) доходности активов, входящих в портфель, изменяются разнонаправлено,

в) доходности активов, входящих в портфель, не связаны друг с другом,

г) нет верного ответа.

4. При допустимом финансовом риске уровень потерь не превышает:

а) прибыли по осуществляемой операции,

б) выручки от реализации,

в) частичной потери собственного капитала,

г) верного ответа нет.

5. Для получения безрисковой комбинации при формировании портфеля необходимо:

а) объединение активов, доходности которых связаны прямой функциональной зависимостью,

б) объединение активов, доходности которых связаны обратной функциональной зависимостью.

6. Для оценки риска портфеля используются:

б) коэффициент корреляции,

в) коэффициент вариации,

г) все вышеперечисленное верно.

7. Какой из методов оценки риска предполагает обратную связь между экспертом и организацией, заказавшей определение степени риска:

б) оценка вероятности наступления неблагоприятного события,

в) оценка финансового состояния организации,

г) верного ответа нет.

8. Определите вид риска: «Он связан с возможностью невыплаты процентов и основной суммы долга заемщиком»:

9. К проявлениям налогового риска относятся:

а) увеличение темпов инфляции,

б) возникновение финансовых потерь в процессе осуществления инвестиционной деятельности организации,

в) изменение порядка и условий уплаты ряда налогов,

г) верного ответа нет.

10. Для управления рисками возможно использование следующих методов:

г) все вышеперечисленное можно использовать.

11. К финансовым рискам относятся:

а) коммерческий риск,

в) инфляционный риск,

г) нет верного ответа.

12. Активный метод управления риском предполагает:

а) осуществление всех операций после проведения мероприятий по предупреждению финансовых потерь,

б) учет в процессе управления риском сложившихся условий хозяйствования,

в) меры по минимизации риска принимаются после наступления рискового события,

г) верного ответа нет.

13. По мнению Марковица инвестор должен принимать решение по выбору портфеля, основываясь на:

а) ковариации и коэффициенте корреляции,

б) ожидаемой доходности и среднеквадратическом отклонении бумаг, входящих в портфель,

в) ожидаемой доходности и среднеквадратическом отклонении портфеля,

г) верного ответа нет.

14. В каком случае дисперсия и среднеквадратическое отклонение дают неверную оценку риска:

а) распределение является симметричным,

б) распределение вероятностей имеет правостороннюю ассиметрию,

в) распределение вероятностей имеет левостороннюю ассиметрию,

г) во всех перечисленных случаях.

15. Модель САРМ:

б) не имеет допущений.

16. β – коэффициент измеряет относительную изменчивость ценной бумаги, рассчитываемую с помощью рыночного индекса ценных бумаг:

а) утверждение верно,

б) утверждение неверно.

17. В модели САРМ наградой за ожидание называется:

в) рыночная доходность,

г) безрисковая доходность.

18. Выберите верное утверждение:

а) добавление в портфель акции, имеющей β>1, увеличивает значение β портфеля,

б) добавление в портфель акции, имеющей β

б) отсутствие безрисковой доходности,

в) операционные издержки подлежат обязательному учету,

г) все вышеперечисленное верно.

22. Безрисковая доходность состоит из:

а) реальной безинфляционной доходности,

б) инфляционной премии,

в) рыночной премии за риск,

г) нет верного ответа.

23. Бета портфеля представляет собой взвешенное среднее коэффициентов бета, входящих в него ценных бумаг, где в качестве весов выступают доли инвестиций в эти бумаги:

а) утверждение верно,

б) утверждение неверно.

24. Если ценная бумага имеет бета менее 1, то:

Источник

Показатели вариации

Классификация показателей вариации

Числовые характеристики вариационного ряда

Относительные показатели вариации

Рассмотрим показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).
Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции (V_R): .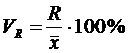

Линейный коэффициент вариации (V):
.
Коэффициент вариации (V_σ): .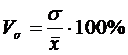

Решение. В разделе «Вид статистического ряда» выбираем Интервальный ряд (рис. 1).

3. На странице ввода данных заполняем исходные данные (рис. 2). При этом открытые интервалы корректируем на закрытые: из открытого интервала «до 3» формируем закрытый 3, из интервала «15 и более» создаем интервал 20.

По умолчанию в отчет включается расчет следующих показателей вариации:
средняя взвешенная, мода, медиана, абсолютные показатели вариации (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение), относительные показатели вариации (коэффициент вариации, линейный коэффициент вариации).

Примечание: несмещенная оценка дисперсии и оценка среднеквадратического отклонения используются при проверке гипотезы о виде распределения, определении относительной ошибки выборки, и в случаях, когда это непосредственно требуется в задании. Во всех остальных случаях данные показатели можно исключить из отчета.

Расчет показателей вариации

Типы вариации

Меры вариации

Вариация существует и в пространстве и во времени.
Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Под вариацией во времени подразумевают изменение значений признака в различные моменты времени. Так, со временем изменяются средняя продолжительность жизни, мнения людей и т.д.
Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).

Прежде, чем определить величину размаха вариации необходимо очистить совокупность от аномальных наблюдений.
Например, нельзя вычислять размах вариации работников какого-либо частного предприятия, если наряду с заработками его работников включен заработок его владельца.
Размах вариации – важный показатель колеблемости признака, но не исчерпывающий его характеристику.

Рассмотрим среднее линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант x_i от по формуле:

(простая средняя),

(взвешенная средняя).

Источник

Что такое коэффициент вариации и для чего он нужен

Коэффициент вариации – это статистический показатель, какой широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько любая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обыкновенно исключают минимальное и максимальное число.

Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна опираться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В цельном, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический разбор, социология, маркетинг и т.д.

Формулы расчета в статистике

Для оценки совокупности значений и их однородности применяют следующие инструменты:

Рассмотрим применение указанных формул на примере оценки среднего возраста трудящихся в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в году между самым младшим и самым старшим из них:

Рассчитаем среднее линейное отклонение. Для этого для начала найдем посредственный возраст в отделе: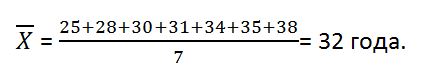Теперь посчитаем среднее линейное отклонение:

Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.

Среднеквадратичное отклонение покажет то же самое, но немало точно:

Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:

Оценка коэффициента вариации

Если со посредственными значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное смысл и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что посредственный возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно выделяться от полученного значения?

В статистике определены следующие критерии оценки:

Если показатель вариации превышает 33%, то выборка почитается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем образце вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.

Если посмотреть на числовой ряд, то видать, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное смыслы, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем образце это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности смыслов.

Читайте также! Выплата дивидендов учредителям ООО и АО в 2019 году

Применение при закупках по 44-ФЗ

Федеральный закон 44-ФЗ регулирует распорядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным стоимостям. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с какой и будут начинаться торги.

Методика определения начальной минимальной цены

Законом предусмотрено 5 методов определения НМЦК:

При этом наиболее предпочтительным и рекомендуемым является именно первоначальный. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко установлены:

Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было привнесено несколько изменений:

Как рассчитать НМЦК

Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать вытекающими способами:

Обычно используется первый способ. Нескольким поставщикам отправляются запросы введённой формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:

Коэффициент вариации в данном случае предзнаменований вид:

Пример расчета

Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков бывальщины получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.

Оценим однородность ценовых предложений линией расчета коэффициента вариации. Для начала рассчитаем среднюю цену:

Теперь необходимо найти среднеквадратичное отклонение:

И, наконец, рассчитываем коэффициент вариации:

V меньше 10%, таким манером, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.

Посчитаем минимальную цену контракта:

Использование в оценке рисков

В финансовом разборе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно всходит, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при неплохом росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.

Декламируйте также! Организация и внедрение бережливого производства на предприятии

Инвестиционные проекты

Как правило, при оценке рисков инвестиционных проектов используются:

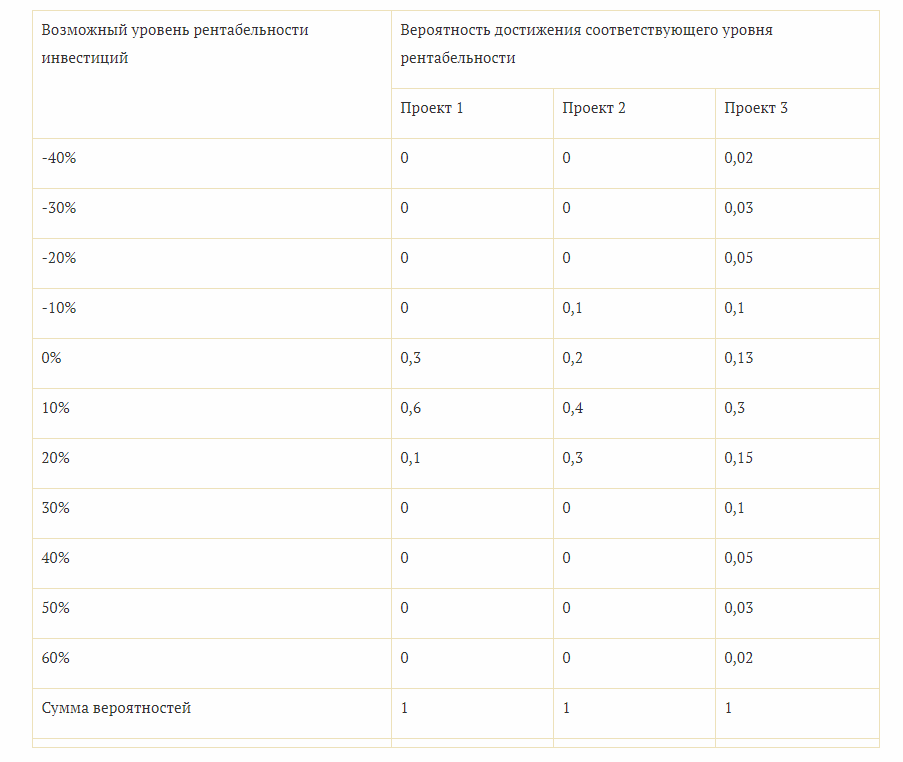
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или другого уровня рентабельности:

В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому немало чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.

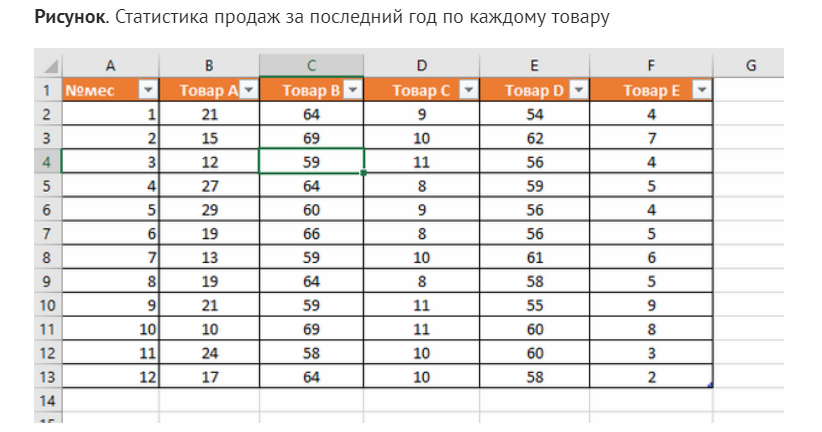
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Так, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:

В этом примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и мощно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.

Ценные бумаги

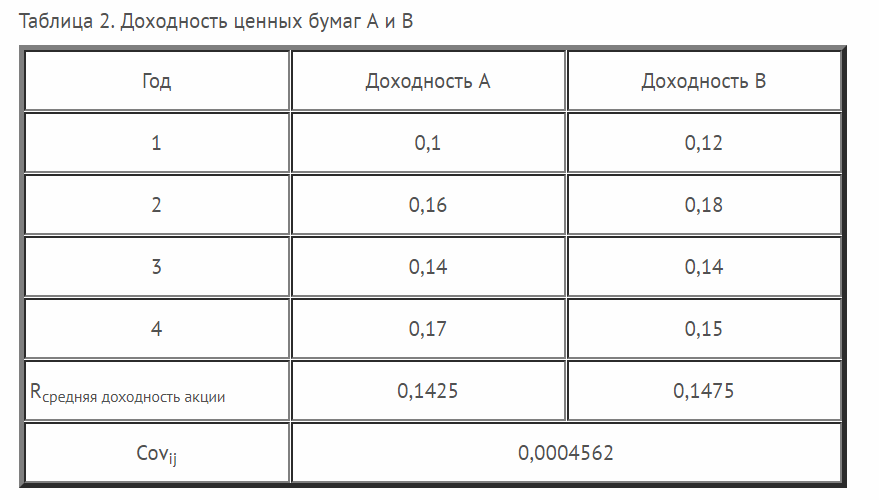
Что касается торговли на бирже, то тут можно оценивать в двух вариантах:

В первом случае, имея эти о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности любой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном интервале. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.

Расчет в MS Excel

Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную весьма трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.

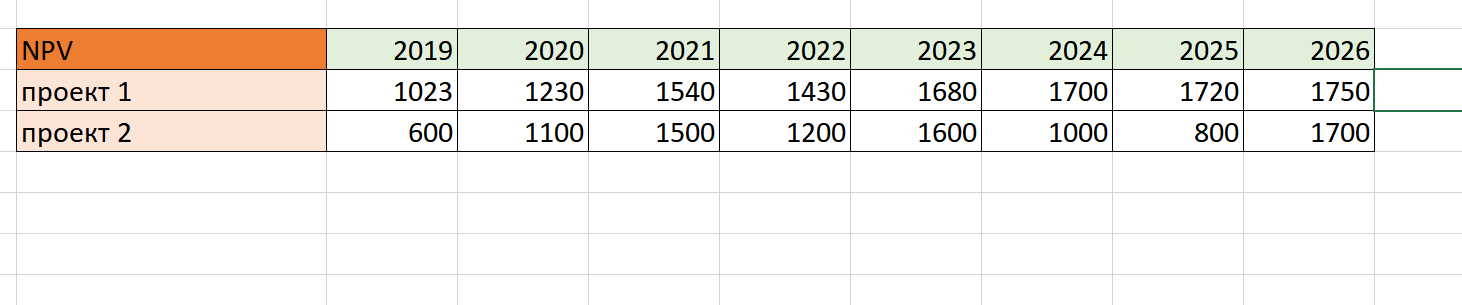
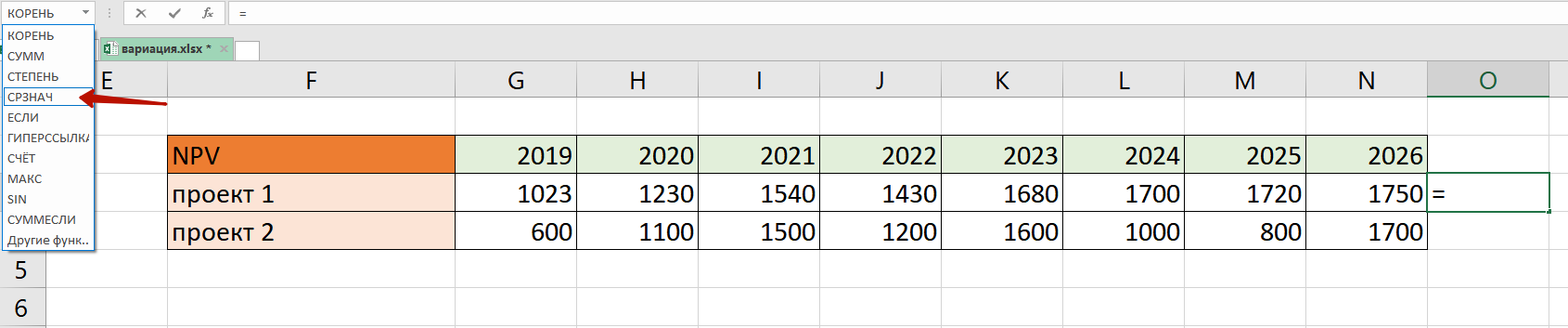
Для начала открываем редактор и создаем таблицу с отправными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.

Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:

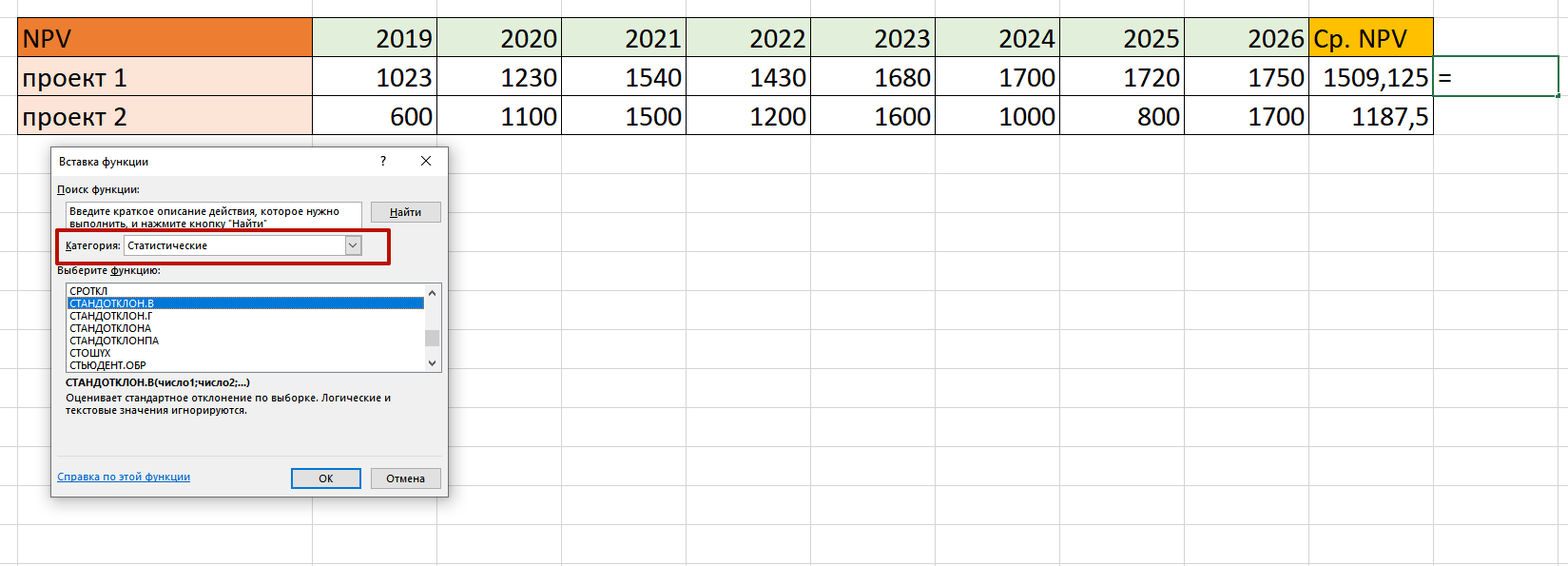
Вышли вот такие значения:

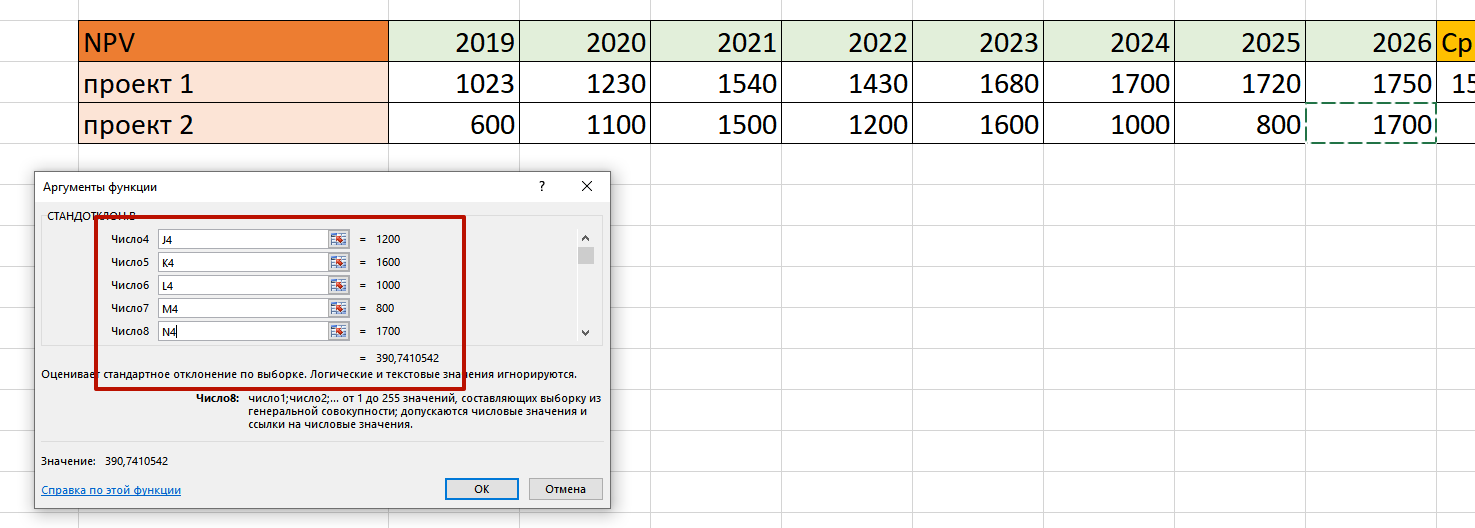
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В

Обратите внимание, что в любую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:

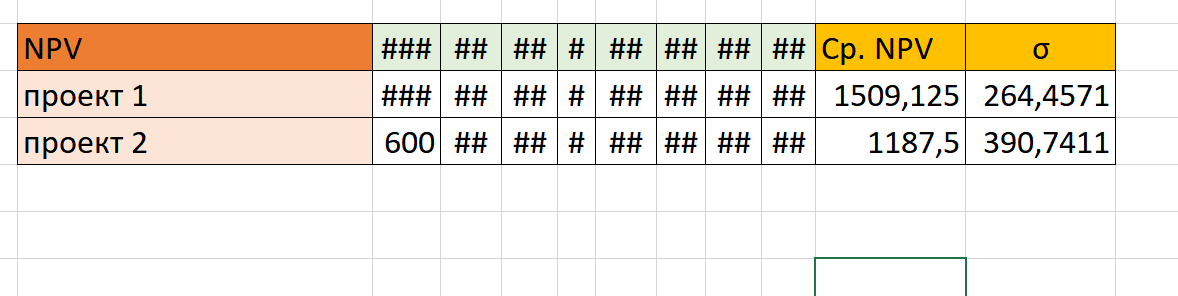
Таким образом, у нас есть рассчитанные посредственные значения доходности и среднеквадратичного отклонения по двум проектам:

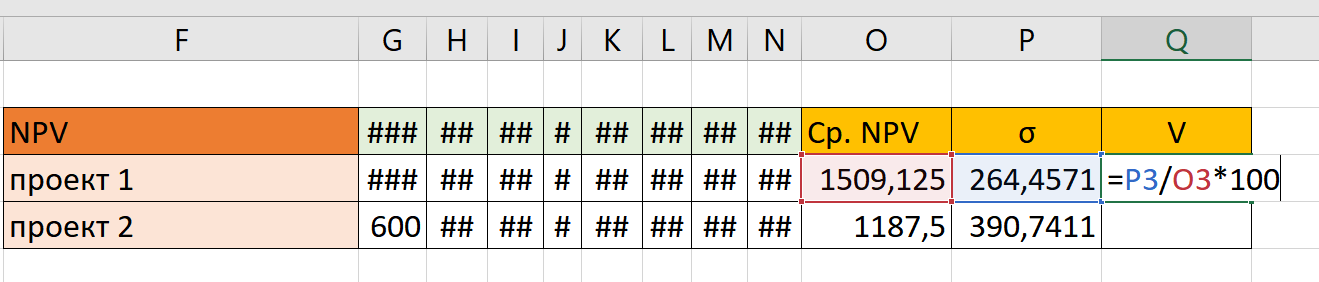
Теперь нам нужно найти коэффициент вариации. Для этого мы попросту вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:

Таким образом, получаем следующие смыслы коэффициента вариации:

Можно сделать вывод о том, что первый проект менее рисковый, чем второй.

Источник