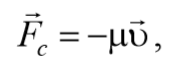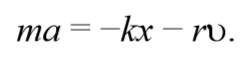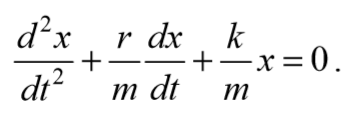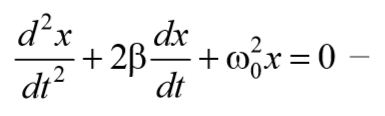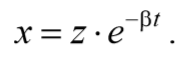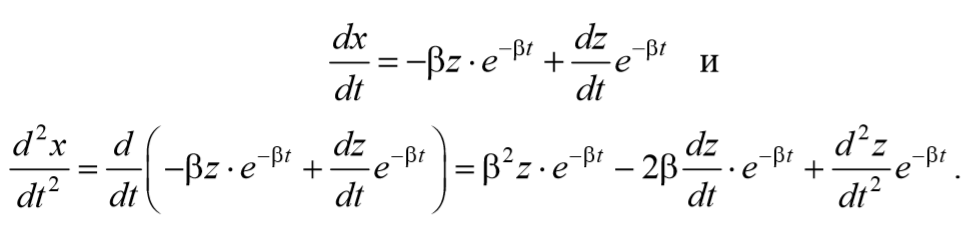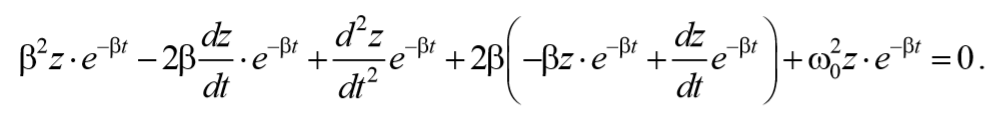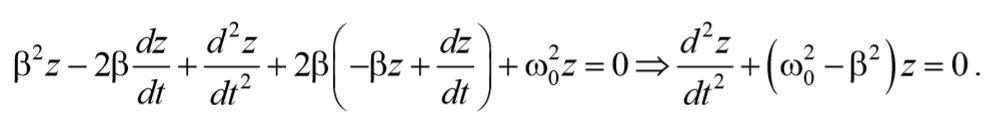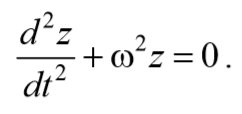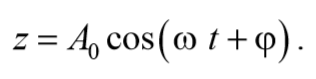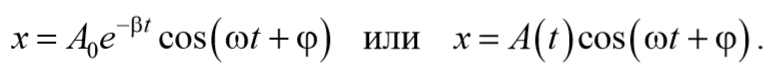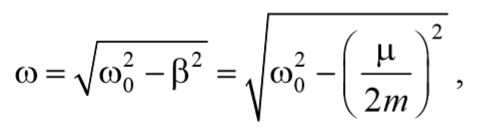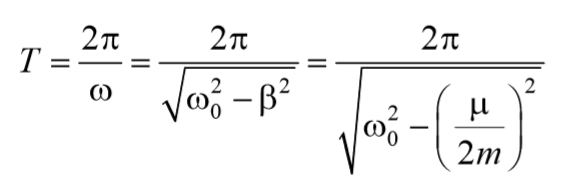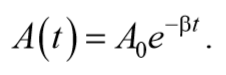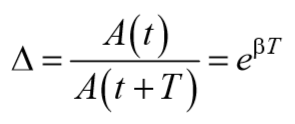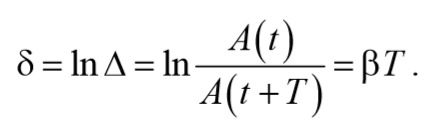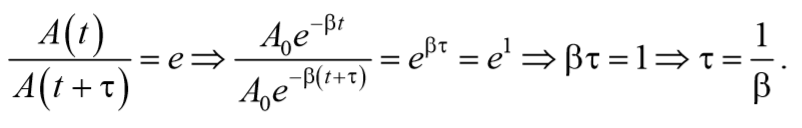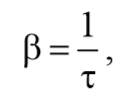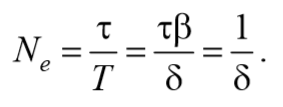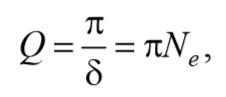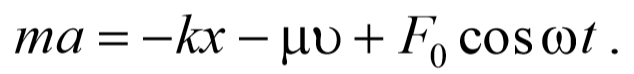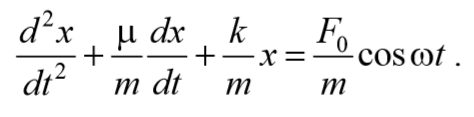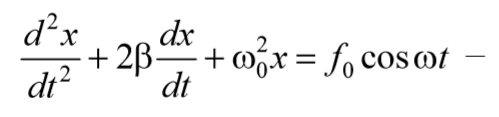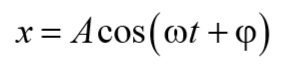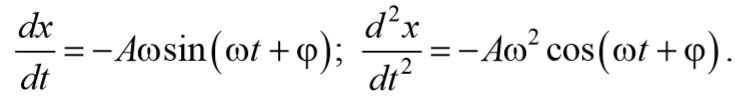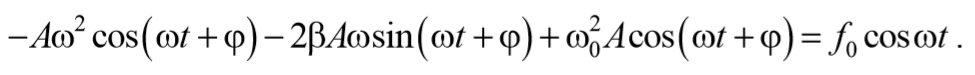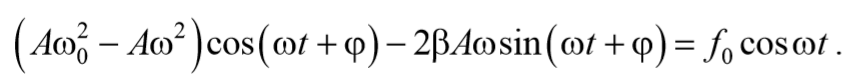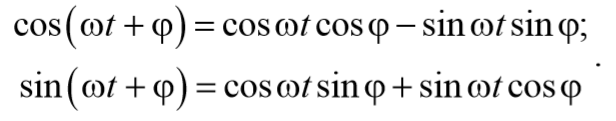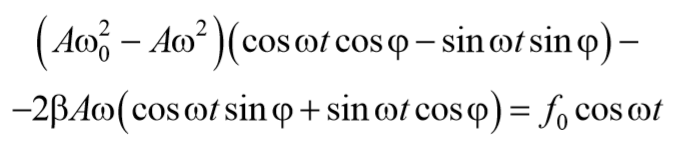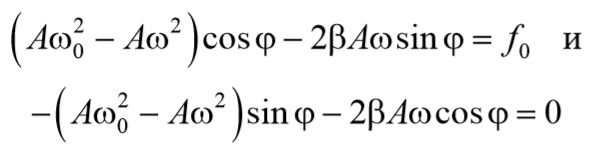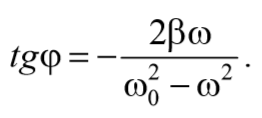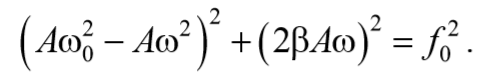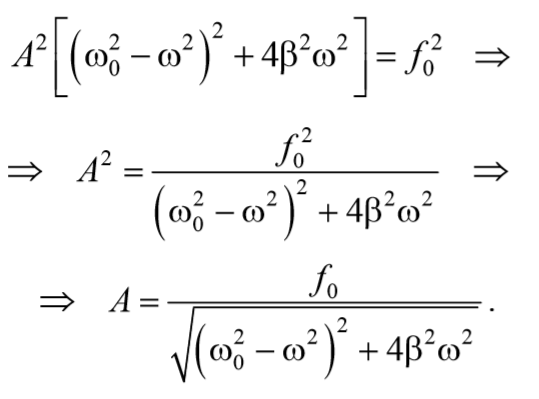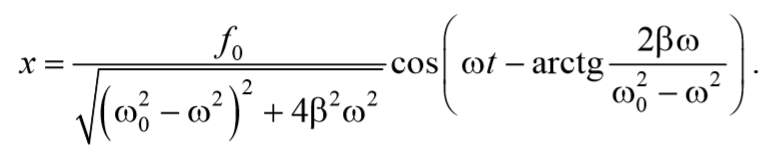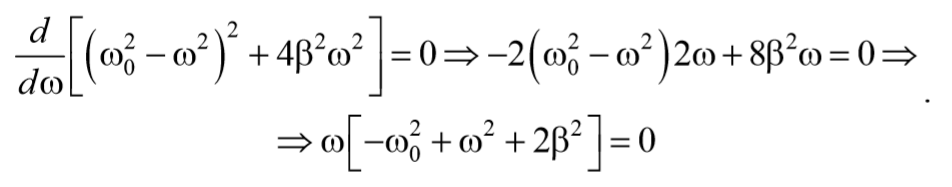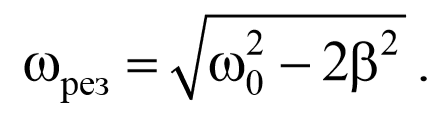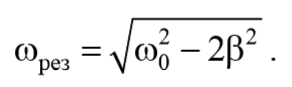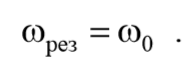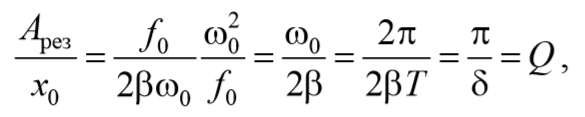Коэффициент затухания в чем измеряется

Что такое коэффициент затухания, в каких единицах он измеряется?

Это дифференциальное уравнение, описывающее колебания заряда конденсатора. Введем обозначения:

, (3.46)

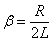
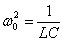
Величину β также как и в случае механических колебаний называюткоэффициентом затухания, а ω₀ – собственной циклической частотой колебаний.

С введенными обозначениями уравнение (3.45) примет вид

(3.47)

Уравнение (3.47) полностью совпадает с дифференциальным уравнением гармонического осциллятора с вязким трением (формула (4.19) из раздела «Физические основы механики»). Решение этого уравнения описывает затухающие колебания вида

где q₀ – начальный заряд конденсатора, ω = 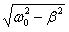– циклическая частота колебаний, φ – начальная фаза колебаний. На рис. 3.17 показан вид функции q(t). Такой же вид имеет и зависимость напряжения на конденсаторе от времени, так как U_C = q/C.

l = ln[A(t)/A(t+T)] = bT= T/t (3.49)

Для характеристики качества колебательного контура вводят величину Q, называемую добротностью

Таким образом, добротность показывает, насколько медленно затухают колебания в контуре.

Из (3.50), (3.49) и (3.46) можно получить выражение для добротности контура через его электрические характеристики

Q = 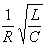(3.51)

Описанный колебательный процесс в контуре совершается без каких-либо внешних воздействий за счет начального запаса энергии, сообщенного контуру. Такие колебания называют свободными. Электрическое сопротивление проводников приводит к затуханию свободных колебаний. Для получения незатухающих колебаний необходимо пополнять убыль энергии в контуре за счет внешних источников. Это можно осуществить, например, включив в состав контура источник переменной э.д.с. Е (рис. 3.18).

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Коэффициент затухания в чем измеряется

Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и (рис. 3.1):

,

где β – коэффициент затухания.

Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:

;

.

Выясним физический смысл χ и β.

Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.

отсюда

Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.

Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда

; ;

.

Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

Если χ = 0,01, то N = 100.

При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , а то круговая частота обращается в нуль ( ), а ( ), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).

Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.

Источник

Лекция №8. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.6. Затухающие гармонические колебания.

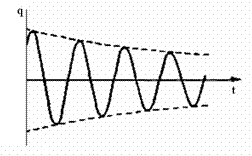
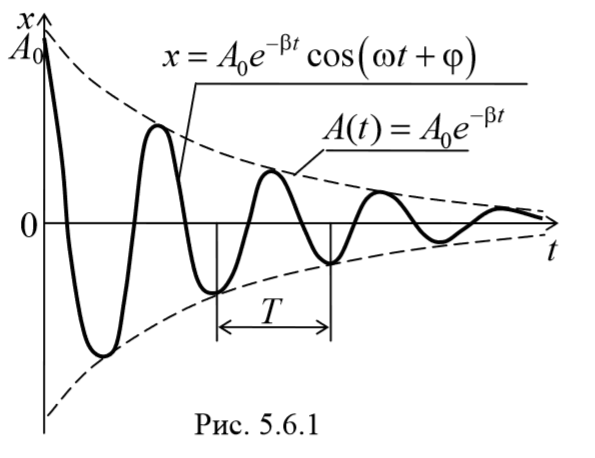
Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающие колебания − это колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. В простейшем, и вместе с тем наиболее часто встречающемся случае, сила сопротивления, вызывающая затухание, зависит от скорости колебательного движения, т. е. ее можно считать прямо пропорциональной скорости

где μ − постоянная, называемая коэффициентом сопротивления.

Знак «минус» обусловлен тем, что сила и скорость имеют противоположные направления. Тогда второй закон Ньютона для гармонических колебаний при наличии сил сопротивления имеет вид

Для решения уравнения (5.6.4) сделаем подстановку

Проведем замену переменных

Подставим (5.6.5 и 5.6.6) в выражение (5.6.4)

Решение уравнения (5.6.8) можно записать в виде

Окончательно, подставляя последнее уравнение в выражение (5.6.5), получаем общее решение дифференциального уравнения затухающих колебаний (5.6.4)

В соответствии с видом полученной функции движение можно рассматривать как гармоническое колебание с частотой

и амплитудой, изменяющейся по закону

5.7. Коэффициент затухания и логарифмический декремент затухания.

Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

т. е. коэффициент затухания обратен по величине промежутку времени, за который амплитуда колебаний уменьшается в e раз.

Для характеристики колебательной системы используется величина

которая называется добротностью колебательной системы.

5.8. Вынужденные колебания.

дифференциальное уравнение вынужденных колебаний.

Будем искать решение уравнения (5.8.3) в виде

предполагая, что результирующее колебание будет совершаться с частотой внешней вынуждающей силы.

Подставим (5.8.4) и (5.8.5) в уравнение (5.8.3)

Чтобы уравнение (69) обратилось в тождество необходимо, чтобы коэффициенты при cosωt и sinωt были равны нулю.

Из выражения (71) получаем

Возведем в квадрат уравнения (70) и сложим

Подставив полученные выражения (71) и (73) в выражение (64) получим уравнение вынужденных колебаний

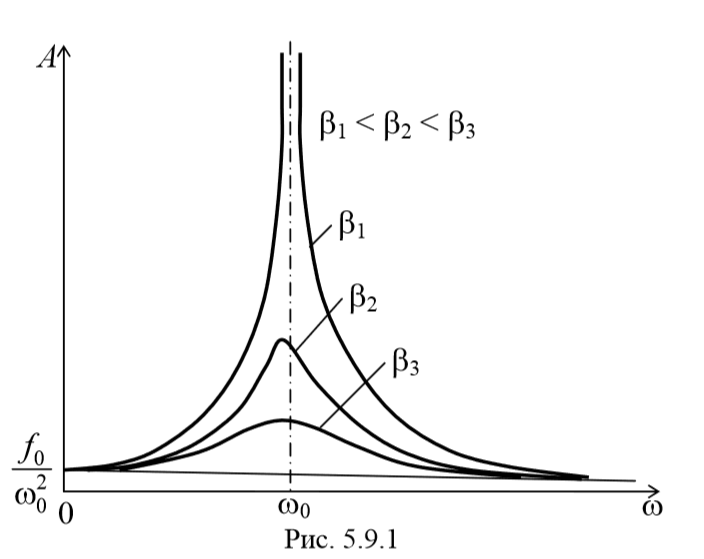
5.9. Резонанс.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой частоте амплитуда колебаний достигает максимального значения.

Продифференцируем это выражение по ω и приравняем к нулю

Подставив это значение в выражение для амплитуды (5.8.13), получим выражение для амплитуды при резонансе

Из последнего уравнения (5.9.3) следует, что при отсутствии сопротивления среды амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота, согласно (5.9.2), при тех же условиях (при β=0 ), совпадала бы с собственной частотой колебаний системы ω₀

При стремлении ω к бесконечности все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.

где δ = βТ – логарифмический декремент затухания (5.7.2); Q – добротность колебательной системы (5.7.6).

Таким образом, добротность Q показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы. Следует отметить, что это справедливо лишь при небольшом затухании.

Источник

СОДЕРЖАНИЕ

Обзор

Коэффициент ослабления описывает степень уменьшения лучистого потока луча при его прохождении через определенный материал. Он используется в контексте:

Коэффициент ослабления называется «коэффициентом ослабления» в контексте

Математические определения

Коэффициент затухания

Коэффициент спектрального полусферического ослабления

Коэффициент направленного затухания

Коэффициент направленного спектрального ослабления

Коэффициент направленного спектрального ослабления по частоте и коэффициент направленного спектрального ослабления по длине волны объема, обозначенные μ _{Ω, ν} и μ _{Ω, λ} соответственно, определяются как

Коэффициенты поглощения и рассеяния

Коэффициент ослабления объема складывается из коэффициента поглощения и коэффициента рассеяния:

Просто глядя на сам узкий луч, эти два процесса невозможно различить. Однако, если детектор настроен для измерения луча, выходящего в разных направлениях, или, наоборот, с использованием неузкого луча, можно измерить, какая часть потерянного лучистого потока была рассеянной и какая была поглощена.

Массовые коэффициенты ослабления, поглощения и рассеяния

Наперовские и декадные коэффициенты затухания

µ иногда называют коэффициентом затухания Напьера или коэффициентом затухания узкого луча Напьера, а не просто «коэффициентом затухания». Термины «декадный» и «наперовский» происходят от основания, используемого для экспоненты в законе Бера – Ламберта для образца материала, в котором участвуют два коэффициента ослабления:

В случае равномерного затухания эти соотношения принимают вид

Коэффициент затухания (Напьера) и декадный коэффициент затухания образца материала связаны с числовой плотностью и количественными концентрациями его ослабляющих азот веществ как

по определению поперечного сечения затухания и молярного коэффициента затухания.

Сечение затухания и молярный коэффициент затухания связаны соотношением

а числовую плотность и количественную концентрацию на

Источник