Конечный автомат что это
Конечные автоматы
Введение
Конечные автоматы являются мощным инструментом для работы. Компиляторы работает на основе конечных автоматов. Любой алгоритм которые вы пишете может быть представлен в виде конечного автомата.
В конечном автомате количесто состояний конечно, а результат его работа определяется по его конченому состоянию (Wikipedia).
Существует несколько видов конечных автоматов:
Детерминированный кончечный автомат (ДКА)
Из любого состояние должен быть только один преход по символову, иначе этот автомат недерминирован.
ДКА является самым удобным из всех конченых автоматов. Его удобнее всего обработаывать, всегда стараются свести задачу к построению ДКА. Но разобрать НКА и ε-НКА также необходимо.
Недетерминированный конечный автомат(НКА)
Предположим нам надо построить автомат, который принимает все строки, состоящие из символов [0, 1], где второй символ будет 0.
ε-Недетерминированный конечный автомат (ε-НКА)
ε-НКА очень похож на НКА, только теперь мы можем преходить по ε. Теперь ничего не считав, мы сможем перейти из одной вершины в другую. 
Принмает теже слова, что и предыдущий
Эквиалетность
Есть свойство у конченых автоматов — это их эквиалетность. ДКА НКА ε-НКА. Благодаря этому мы можем спокойно из ε-НКА сделать ДКА, это нам сильно пригодится.
Вкратце, разобрав какие бывают автоматы, мы можем перейти к более подробному изучению их реализации
Реализация
Обработка автомата
Как же можно проверить принимает ли данный кончечный автомат строку.
Для ДКА все очевидно. Мы храним матрицу преходов, текущее состояние (когда мы ничего не считали, тек. сотояние = начальное состояние) и терминальные вершины. Считываем по одному символу, и переходим в состояние по матрице перехода.
Для НКА вместо текущего состояния мы храним множество текущих состояний. Разберем НКА данный выше.
Пусть мы хотим перейти по символу 0. Текущее множество состояний — множество, состоящее из одной вершины — начальной. У нас есть два прехода по символу 0 => множество состояний у нас будет
Обработка ε-НКА похожа на обработку НКА. Предположим наше текущее множество S. Перед считываением следущего символа: для всех q ∈ S добавить в множество S вершину достигаемую из q по символу ε.
Детерминация автомата
Перевести автомат из ДКА в НКА легко. Нам просто ничего не нужно делать, т.к. ДКА это обобщенный случай НКА.
Но что делать если мы хотим превести из ε-НКА в ДКА (НКА является обобшенным случаем ε-НКА). Этот процесс называется детерминацией автомата.
Начнем обоходить наш ε-НКА, например, DFS-ом. Вершиной графа является множество текущих состояний. Состояниями нового ДКА будут все вершины графа. При переходе к новой веришне мы выбираем символ по которому хотим перейти, и добавляем этот переход. Приведу псевдокод DFS-a для большой ясности:
Если в множестве есть терминальное состояние, то состояние нового ДКА будет тоже терминальным.
К сожалению число состояние нового ДКА будет расти экспоненциально, что не очень хорошо, т.к. это будет потреблять много памяти.
Алгоритм минимизации ДКА
Любой ДКА имеет эквиалетный ему ДКА с минимальным числом состояний. Как его «сжать»? Заметим, что неразличимые вершины мы можем соединить в одну.
Что такое различимое состояние?
Состояние p и q являются различимыми, если есть такое слово s, что преходя из вершины p по слову s мы попадаем в терминальное состояние, а из вершины q в не-терминальное, или наоборот.
1) Терминальное и не-терминальное состояние являются различимыми. Перейдем по пустому слову и окажемся в двух различимых состояниях.
2) Состояния a и b различимы. Если существуют состояния c и d, и из c есть переход по символу x в состояние a, а из веришны d есть переход по символу x в состояние b, то состояние a и b различимы.
Мы нашли все различимые состояния. Теперь нам надо «схлопнуть» все неразличимые.
Регулярные выражения
Регулярные варжения напрямую связаны с конечными автоматами. Введем некоторые обозначения:
∅ — пустое множество.
ε — строка, которая не сожержит символов.
Пусть A и B регулярные выражения. L(A) и L(B) — кончечные языки, которые данные регулярные варжения задают.
Это основные операции прменимые к регулярным варжением. Можно всетрить и другие, но все они могут быть представлены операциями данными выше.
Вот представление основных операций регулярных выражений в виде ε-НКА.


Дале разбираем это выражение рекурсивным спуском и строим ε-НКА.
Чтобы обработать Регулярное выражение построим для ε-НКА, а потом получим из ε-НКА ДКА, который очень легко обрабатывать.
Конечные автоматы на страже порядка
При разработке сложных систем часто сталкиваешься с проблемой прозрачности кода, точным описанием бизнес-логики и масштабирования решения. Однажды нам поставили задачу: реализовать функциональность тарифов, в которой много бизнес-логики. При этом сроки были сжаты, да ещё и повышенные финансовые риски. Чтобы решить эту задачу быстро, эффективно и прозрачно, мы решили использовать конечные автоматы (state machine).
Суть задачи
Тариф в «Юле» — это набор платных опций по размещению и продвижению объявлений. Они дают пользователям дополнительные преимущества, вроде расширенного личного кабинета в веб-версии сервиса, использования раздела портфолио и прочего.
Также у нас есть понятие пакета — платный набор из определённого количества размещений объявлений. Удельно получается дешевле, чем когда оплачиваешь размещения разово.
Бизнес попросил добавить в мобильное приложение возможность всячески редактировать услугу тарифов. Продакт-менеджеры придумали очень крутую и гибкую схему логики, под которую пришлось бы сделать очень много экранов и переходов. Вот лишь четверть всей схемы, это только редактирование, а есть ещё создание, оплата, планирование и так далее.
Естественно, мы заподозрили, что решение получится очень громоздким. Например, с тарифами задача подразумевала 7 полноценных экранов, массу различных диалогов и уведомлений. От сервера необходимо было сразу получать определенные данные. К этому добавилась и обработка различных состояний доступности редактирования выбранных значений; предвыбранные значения, которые нам приходят с сервера; возможность выбирать значения только на увеличение (речь о возможности запланировать тариф с большими значениями относительно текущих настроек тарифа). И многое другое. С пакетами была похожая картина, но меньше масштабом.
К тому же было еще два небольших условия от бизнеса:
Выбор решения
Первый вариант самый очевидный: флаги. Их можно описать очень много. Например, вот небольшое условие, которое отображает шапку тарифа:
Увы, такой вариант тяжело расширять. Когда добавится новое условие, придётся ветвить схему еще сильнее.
Второй вариант: добавление переменных с состояниями. На их основе можно решать, что отрисовывать. Но такому способу не хватает гибкости.
Третий вариант: найти что-то более описываемое, понятное и масштабируемое. Конечно же, это конечные автоматы (машины состояний).
Конечный автомат — это модель дискретного устройства, которое имеет в себе определенный набор правил, обычно один вход и один выход. И в каждый момент времени автомат находится в одном состоянии из множества описанных. У автомата есть API, по которому можно переключить состояние, и если это некорректное переключение, то мы узнаем об ошибке. Следуя этой концепции очень легко структурировать код и сделать его читаемым. Такой код проще отлаживать и контролировать на всех этапах. Простенький конечный автомат может выглядеть так, и его очень легко расширять:
Конечные автоматы
Конечные автоматы прекрасно помогают в реализации бизнес-логики. Ведь мы точно описываем поведение системы при любом событии. Поэтому мы решили использовать этот подход. Описали нашу схему:
В ней можно иногда запутаться, однако всё, что было необходимо на момент реализации, здесь есть. Но нарисовав эту схему, мы поняли, что всё-таки надо понять, что и как мы будем реализовывать.
Есть несколько вариантов. Первый: пишем всё сами. Второй: берём одну из своих старых узкоспециализированных реализаций и дорабатываем. И третий вариант: используем готовое решение.
У самописного решения есть очевидные достоинства и недостатки. К первым относится лёгкость изменения и язык Kotlin. Правда, на разработку требуется немало времени. К тому же могут быть баги, которые придётся исправлять.
Начали смотреть на сторонние решения. Сначала выбрали библиотеку Polidea. Но у неё оказалось довольно много недостатков на наш взгляд: она написана на Java, имеет проблемы с поддержкой и трудно дорабатывается.
Тогда мы обратили внимание на библиотеку Tinder. Достоинств у неё оказалось больше, чем недостатков, что и сыграло позднее в её пользу. Она написана на Kotlin, у неё удобная DSL, библиотеку регулярно обновляют. А её главный недостаток — трудно дорабатывается. Но всё же мы остановились на Tinder.
Библиотека Tinder
Состояния переключаются просто: передаём в Transition объекта stateMachine событие, которое хотим отправить. В stateMachine есть описание всех возможных состояний. А внутри них мы можем описать те события, которые могут произойти.
Реализация
Чтобы реализовать нашу бизнес-логику, кроме состояний нужно было описать и данные. Мы решили использовать один объект, который станет постепенно заполняться, пока пользователь идет по конечному автомату. В объекте есть набор параметров, либо влияющих на часть нашей функциональности, либо отражающих предустановку каких-то данных, либо содержащих какие-то вспомогательные данные.
По мере реализации схема разрослась: получилось около 30 состояний и 100 переходов. И поскольку всё содержалось в одном файле, ориентироваться стало довольно сложно. А искать баги — ещё тяжелее, потому что когда из одного состояния перешел в другое, то появились какие-то данные и не можешь понять, в чём проблема.
На помощь пришла декомпозиция. Раз мы смогли сделать один конечный автомат, то сможем сделать ещё. Так мы из одного автомата сделали шесть.
С одной стороны, кажется, что мы увеличили себе работу. С другой стороны, мы стали лучше ориентироваться в коде. Стали понимать бизнес-схему и логику нашего приложения. Всё стало проще.
У нас есть базовый автомат, который управляет несколькими маленькими. Каждый из них отвечает за свой фрагмент функциональности. И когда продакт-менеджеры просят добавить что-то ещё, нам не приходится менять все переходы большого автомата. Достаточно поменять один маленький.
Например, так выглядит автомат выбора данных:
Автомат сборки пакета:
Автомат сборки тарифа:
А это автомат оплаты:
Приятный бонус
Кроме лёгкости расширения «модульные» конечные автоматы сильно упростили нам тестирование. Чтобы начать покрывать их тестами, можно написать небольшие обёртки, позволяющие указать начальное состояние, переход и ожидаемое состояние. Пример теста:
Было очень приятно осознать, что авторы библиотеки позаботились и о простоте тестирования.
В заключение
Если вы уже сталкивались с конечными автоматами и не понимали, зачем их использовать, то надеюсь, что мой рассказ помог вам разобраться в этом. Иногда они действительно нужны, и с ними очень приятно работать.
Да, конечные автоматы не всегда оправданы. Поэтому к их использованию надо подходить, взвесив все «за» и «против».
Конечный автомат
Из Википедии — свободной энциклопедии
Коне́чный автома́т (КА) — (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. Является частным случаем абстрактного дискретного автомата, число возможных внутренних состояний которого конечно.
При работе на вход КА поступают последовательно входные воздействия, а на выходе КА формирует выходные сигналы. Обычно под входными воздействиями принимают подачу на вход автомата символов одного алфавита, а на выход КА в процессе работы выдаёт символы в общем случае другого, возможно даже не пересекающегося со входным, алфавита.
Помимо конечных автоматов существуют и бесконечные дискретные автоматы — автоматы с бесконечным числом внутренних состояний, например, машина Тьюринга.
Переход из одного внутреннего состояния КА в другое может происходить не только от внешнего воздействия, но и самопроизвольно.
Различают детерминированные КА — автоматы, в которых следующее состояние однозначно определяется текущим состоянием и выход зависит только от текущего состояния и текущего входа, и недетерминированные КА, следующее состояние у которых в общем случае неопределённо и, соответственно, не определён выходной сигнал. Если переход в последующие состояния происходит с некоторыми вероятностями, то такой КА называют вероятностным КА.
Примерами физической реализации КА могут служить любые цифровые системы, например, компьютеры или некоторые логические узлы компьютеров с памятью — триггеры и другие устройства. Комбинационная последовательная логика не может являться КА, так как не имеет внутренних состояний (не имеет памяти).
С абстрактной точки зрения КА изучает раздел дискретной математики — теория конечных автоматов.
Конечный автомат: теория и реализация
Авторизуйтесь
Конечный автомат: теория и реализация
Конечный автомат — это некоторая абстрактная модель, содержащая конечное число состояний чего-либо. Используется для представления и управления потоком выполнения каких-либо команд. Конечный автомат идеально подходит для реализации искусственного интеллекта в играх, получая аккуратное решение без написания громоздкого и сложного кода. В данной статье мы рассмотрим теорию, а также узнаем, как использовать простой и основанный на стеке конечный автомат.
Мы уже публиковали серию статей по написанию искусственного интеллекта при помощи конечного автомата. Если вы еще не читали эту серию, то можете сделать это сейчас:
Примечание автора Хоть в статье используются ActionScript 3 и Flash, вы с легкостью можете писать на удобном для вас языке.
Что такое конечный автомат?
Конечный автомат (или попросту FSM — Finite-state machine) это модель вычислений, основанная на гипотетической машине состояний. В один момент времени только одно состояние может быть активным. Следовательно, для выполнения каких-либо действий машина должна менять свое состояние.
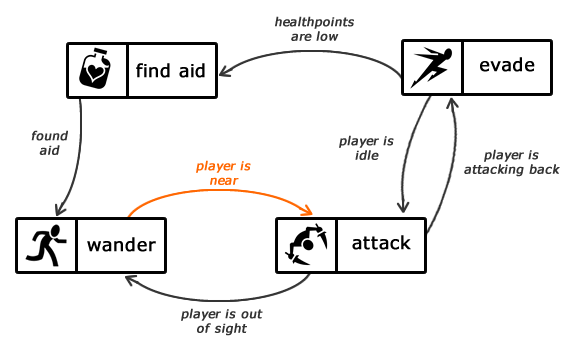
Конечные автоматы обычно используются для организации и представления потока выполнения чего-либо. Это особенно полезно при реализации ИИ в играх. Например, для написания «мозга» врага: каждое состояние представляет собой какое-то действие (напасть, уклониться и т. д.).
Описание состояний автомата
Конечный автомат можно представить в виде графа, вершины которого являются состояниями, а ребра — переходы между ними. Каждое ребро имеет метку, информирующую о том, когда должен произойти переход. Например, на изображении выше видно, что автомат сменит состояние «wander» на состояние «attack» при условии, что игрок находится рядом.
Планирование состояний и их переходов
Реализация конечного автомата начинается с выявления его состояний и переходов между ними. Представьте себе конечный автомат, описывающий действия муравья, несущего листья в муравейник:
Описание состояний интеллекта муравья
Отправной точкой является состояние «find leaf», которое остается активным до тех пор, пока муравей не найдет лист. Когда это произойдет, то состояние сменится на «go home». Это же состояние останется активным, пока наш муравей не доберется до муравейника. После этого состояние вновь меняется на «find leaf».
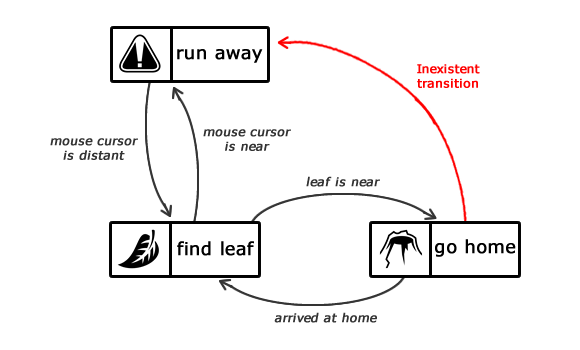
Если состояние «find leaf» активно, но курсор мыши находится рядом с муравьем, то состояние меняется на «run away». Как только муравей будет в достаточно безопасном расстоянии от курсора мыши, состояние вновь сменится на «find leaf».
Обратите внимание на то, что при направлении домой или из дома муравей не будет бояться курсора мыши. Почему? А потому что нет соответствующего перехода.
Описание состояний интеллекта муравья. Обратите внимание на отсутствие перехода между «run away» и «go home»
Реализация простого конечного автомата
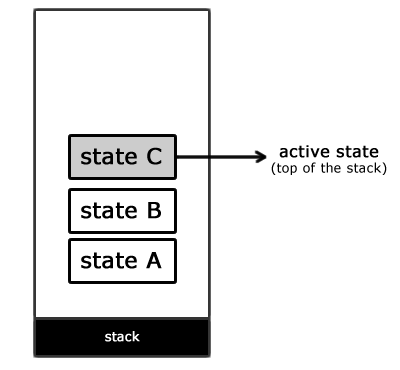
Конечный автомат можно реализовать при помощи одного класса. Назовем его FSM. Идея состоит в том, чтобы реализовать каждое состояние как метод или функцию. Также будем использовать свойство activeState для определения активного состояния.
Всякое состояние есть функция. Причем такая, что она будет вызываться при каждом обновлении кадра игры. Как уже говорилось, в activeState будет храниться указатель на функцию активного состояния.
Метод update() класса FSM должен вызываться каждый кадр игры. А он, в свою очередь, будет вызывать функцию того состояния, которое в данный момент является активным.
Метод setState() будет задавать новое активное состояние. Более того, каждая функция, определяющая какое-то состояние автомата, не обязательно должна принадлежать классу FSM — это делает наш класс более универсальным.
Использование конечного автомата
Давайте реализуем ИИ муравья. Выше мы уже показывали набор его состояний и переходов между ними. Проиллюстрируем их еще раз, но в этот раз сосредоточимся на коде.
Описание состояний интеллекта муравья, сосредоточенное на коде
Наш муравей представлен классом Ant, в котором есть поле brain. Это как раз экземпляр класса FSM.
Класс Ant также содержит свойства velocity и position. Эти переменные будут использоваться для расчета движения с помощью метода Эйлера. Функция update() вызывается при каждом обновлении кадра игры.
Для понимания кода мы опустим реализацию метода moveBasedOnVelocity(). Если хотите узнать поподробнее на тему движения, прочитайте серию статей Understanding Steering Behaviors.
Ниже приводится реализация каждого из методов, начиная с findLeaf() — состояния, ответственного за поиск листьев.
Состояние goHome() — используется для того, чтобы муравей отправился домой.
И, наконец, состояние runAway() — используется при уворачивании от курсора мыши.
Улучшение FSM: автомат, основанный на стеке
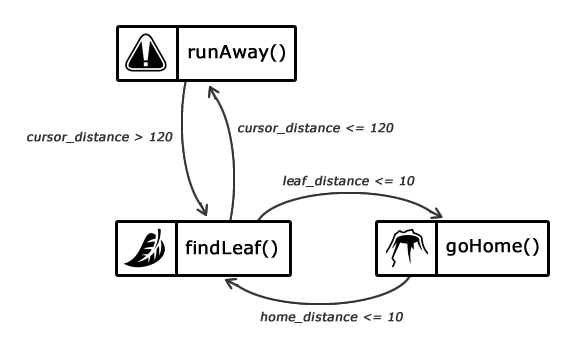
Представьте себе, что муравью на пути домой также нужно убегать от курсора мыши. Вот так будут выглядеть состояния FSM:
Обновленное описание состояний интеллекта муравья
Кажется, что изменение тривиальное. Нет, такое изменение создает нам проблему. Представьте, что текущее состояние это «run away». Если курсор мыши отдаляется от муравья, что он должен делать: идти домой или искать лист?
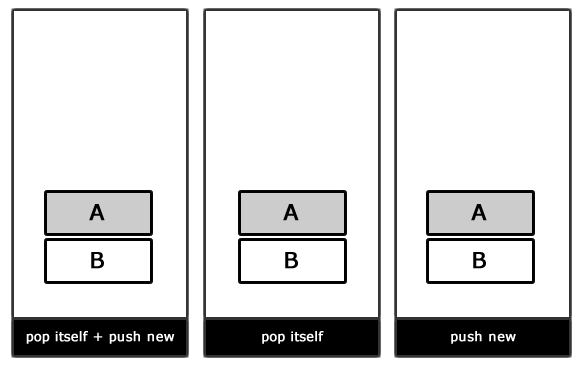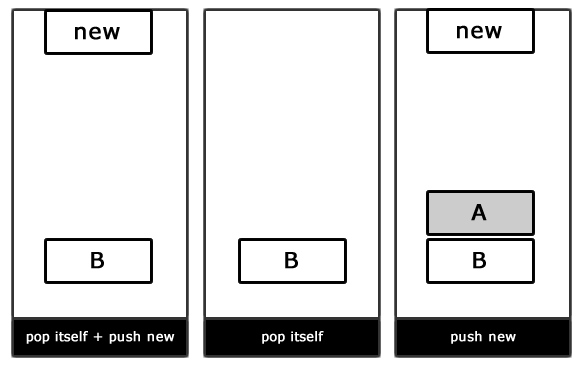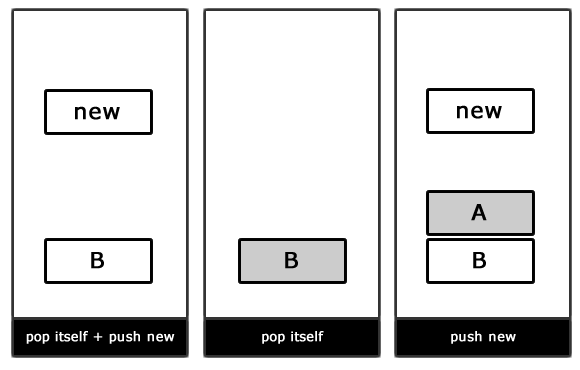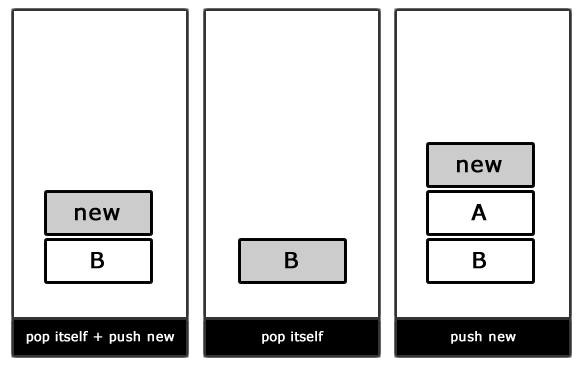
Решением такой проблемы является конечный автомат, основанный на стеке. В отличие от простого FSM, который мы реализовали выше, данный вид FSM использует стек для управления состояниями. В верхней части стека находится активное состояние, а переходы возникают при добавлении/удалении состояний из стека.
Конечный автомат, основанный на стеке
А вот и наглядная демонстрация работы конечного автомата, основанного на стеке:
Переходы в FSM, основанном на стеке
Реализация FSM, основанного на стеке
Такой конечный автомат может быть реализован так же, как и простой. Отличием будет использование массива указателей на необходимые состояния. Свойство activeState нам уже не понадобится, т.к. вершина стека уже будет указывать на активное состояние.
Обратите внимание, что метод setState() был заменен на pushState() (добавление нового состояния в вершину стека) и popState() (удаление состояния на вершине стека).
Использование FSM, основанного на стеке
Важно отметить, что при использовании конечного автомата на основе стека каждое состояние несет ответственность за свое удаление из стека при отсутствии необходимости в нем. Например, состояние attack() само должно удалять себя из стека в том случае, если враг был уже уничтожен.
Вывод
Конечные автоматы, безусловно, полезны для реализации логики искусственного интеллекта в играх. Они могут быть легко представлены в виде графа, что позволяет разработчику увидеть все возможные варианты.
Реализация конечного автомата с функциями-состояниями является простым, но в то же время мощным методом. Даже более сложные переплетения состояний могут быть реализованы при помощи FSM.
Конечные автоматы в реальной жизни: где мы их используем и почему
Привет, меня зовут Антон Субботин, я выпускник курса «Мидл фронтенд-разработчик» в Яндекс.Практикуме. Не так давно мы с наставником курса Захаром Овчаровым провели вебинар, посвящённый конечным автоматам и их практическому применению. Вебинар получился интересным, а потому по его следам я написал статью для Medium на английском языке. Также есть запись вебинара. Однако мы с Захаром решили сделать ещё кое-что: перевести на русский и немного расширить статью, чтобы вы могли никуда не ходить и прочитать её здесь, на Хабре. Разобрались с предысторией — теперь начнём погружение в мир конечных автоматов.
Конечный автомат с счастливым и грустным Васькой
Конечные автоматы
Для начала дадим определение: конечный автомат (finite-state machine, FSM) — это математическая абстракция, модель, которая может находиться только в одном из конечного числа состояний в каждый конкретный момент времени. Автомат умеет переходить из одного состояния в другое в ответ на данные, которые подаются на вход; изменение состояния называется переходом. FSM определяется списком его состояний, начальным состоянием и инпутами, запускающими переходы.
Вот и всё — у нашего автомата должно быть конечное количество состояний, он находится в одном из них в конкретный момент времени, а ещё у него есть правила, определяющие переход между состояниями. Для наглядности представим кота по имени Васька, который может быть счастливым или грустным. Прямо сейчас Васька счастлив. Когда вы уходите, он грустит, а когда возвращаетесь — снова счастлив. Вы можете возразить, что кошкам наплевать, дома вы или нет, но наш Васька не такой. Вы, наверное, уже видите связь:
Это самый простой пример, который мне удалось придумать. В статье мы обсудим примеры использования подобных автоматов и напишем собственную реализацию с нуля, а также решим пару задач при помощи конечного автомата. Вперёд!
Примеры использования
FSM можно использовать для описания алгоритмов, позволяющих решать те или иные задачи, а также для моделирования практически любого процесса. Несколько примеров:
Проверка бинарного кода
Создадим наш первый автомат. Посмотрите последний пример по ссылке или пишите код по ходу чтения. Будем реализовывать допускающий автомат с конечным состоянием. Это конечный автомат, цель которого — определить, принадлежит ли некая строка определённому языку, и либо допустить, либо отклонить её. Мы уже обсуждали начальное и другие состояния и переходы, однако теперь потребуется определить ещё два параметра:
Вот наш автомат, детерминированный акцептор с конечным состоянием:
У нас получился автомат на основе классов, способный проверять случайные значения на соответствие своим определениям. Чтобы использовать его, мы должны создать экземпляр со всеми необходимыми параметрами. Давайте разберёмся.
Схема акцептора бинарного кода
Помните, что переходы происходят в каждой итерации, и у любого состояния имеются переходы для символов 0 и 1. Это можно интерпретировать так:
Использование и тестирование
Получилось! Обратите внимание: нам не нужно указывать все возможные символы для каждого состояния — когда автомат встречает не прописанный в алфавите символ, он заканчивает работу.
Сложная форма
Пример с проверкой бинарного кода — довольно тривиальный. Вряд ли вам часто придётся решать такие задачи, если придётся вообще. Давайте рассмотрим ещё один пример — создадим форму с несколькими состояниями в UI-ориентированном FSM. Код автомата доступен на CodeSandbox, вы можете перейти к нему или попробовать написать его самостоятельно.
Для начала создайте новый проект в React:
Структура проекта должна выглядеть так:
App.js и index.js не требуют изменений. FSM.js будет содержать новую реализацию FSM, напишем её:
Обратите внимание, что мы удалили алфавит и состояния. Теперь у нас есть только два параметра, которые нужно определить:
Давайте протестируем код на нашем примере с Васькой. Создайте файл test.js :
Теперь запустите его с помощью node test.js (убедитесь, что вы находитесь в каталоге файлов). Вывод на консоли должен выглядеть так:
Автомат определённо работает! Наконец, давайте отреагируем на изменение настроения Васьки:
Запустите автомат снова.
Васька теперь всегда счастлив, потому что мы не бросаем его. Если после перехода состояние — грустное, срабатывает триггер возвращения, и кот снова счастлив.
Похоже, всё работает нормально. Переходим к реальной задаче: создадим анкету с несколькими состояниями, которые нужны для управления интерфейсом. Допустим, мы хотим узнать имя и профессию пользователя. Если пользователь — студент, мы спросим, в каком университете он учится. В противном случае спросим, где он работает. Пользователь может вернуться с этапа Education / Work обратно к этапу Personal, на котором мы спрашиваем имя. Наконец, он может отправить анкету при выборе любого из вариантов занятости.
Небольшая диаграмма, чтобы стало понятнее:

Автомат, определяющий нашу анкету
Когда стало ясно, какие состояния у нас есть и как они соотносятся друг с другом, мы можем приступить к работе над проектом. Первое: нужно установить дополнительные зависимости:
Файл questionnaireMachine.js создаёт и экспортирует экземпляр Questionnaire FSM:
Questionnaire FSM
Следующим шагом будет создание презентационного слоя проекта — самой анкеты. Мы разделим его на три отдельных компонента:
Теперь займёмся компонентом карточки:
Кнопки в нижней части компонента используют указанные действия как listener для события клика. Вот почему мы здесь передаём функции, изменяющие состояние FSM: так компонент анкеты сможет обновить uiState и отобразить нужную карточку.
Последняя мелочь — компонент прелоадера. Здесь нет ничего интересного, просто анимированная точка:
Наконец, добавляем анкету в компонент приложения. Корневой компонент со стилями:
В итоге должно получиться нечто похожее на это. Если да, возрадуйтесь — вы только что создали анкету на основе конечного автомата! Если что-то не работает, сравните свой код с содержимым этой песочнице. У вас наверняка получится наверстать упущенное.
Анкета, которую мы только что создали, разделена на логический и презентационный слои, поэтому при желании её поведение или внешний вид легко скорректировать. Одну реализацию конечного автомата можно использовать в любом числе компонентов — этот подход обеспечивает предсказуемую и стабильную работу приложения.
И ещё кое-что. Несмотря на то, что написать собственный FSM с нуля — очень полезный опыт, для рабочих задач я рекомендую использовать готовые библиотеки, например XState. Там есть и подробная документация, и все необходимые инструменты для работы (их, возможно, даже больше, чем нужно).