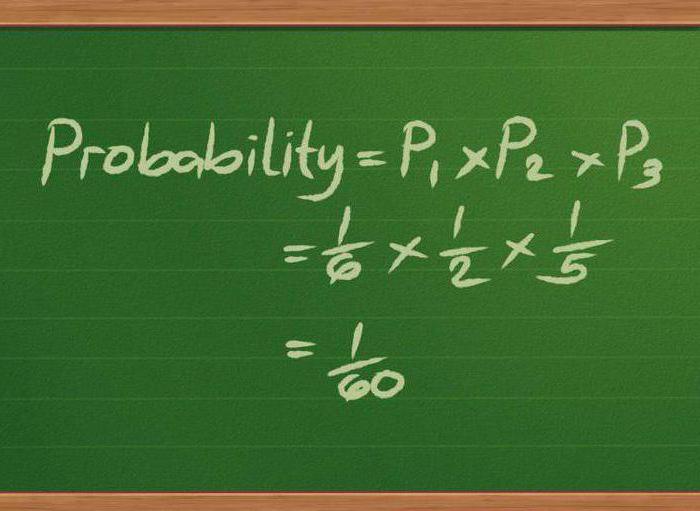Концепция стохастического воздействия предполагает что
«Стохастический» – это слово, которое физики, математики и другие ученые используют для описания процессов, обладающих элементом случайности. Происхождение его древнегреческое. В переводе оно означает «умеющий угадывать».
Значение слова «стохастический»
Таким образом, можно заметить, что техническое значение данного понятия не точно соответствует его словарному (лексическому) значению. Некоторые авторы используют выражение «стохастический процесс» как синоним понятия «случайный процесс».
Стохастичность в математике
Употребление данного термина в математике в настоящее время широко распространено. К примеру, существует такое понятие в теории вероятности, как стохастический процесс. Его итог нельзя определить по изначальному состоянию данной системы.
Употребление в математике понятия «стохастичность» относят к трудам Владислава Борцкевича. Именно он использовал данный термин в значении «выдвигать гипотезы». В математике, в особенности в таком разделе этой науки, как теория вероятности, область случайных исследований играет большую роль. Существует, к примеру, такое понятие, как стохастическая матрица. Колонки или строки данной матрицы в сумме дают единицу.
Стохастическая математика (финансовая)
Данный раздел математики анализирует финансовые структуры, действующие в условиях неопределенности. Он призван находить самые рациональные методы управления финансовыми средствами и структурами, учитывая такие факторы, как стохастическая эволюция, риск, время и др.
В науке принято выделять следующие структуры и объекты, которые используются в финансовой математике в целом:
Основным объектом изучения финансовой математики стохастической является именно последний из них. Данный раздел базируется на таких дисциплинах, как статистика случайных процессов, теория случайных процессов и др.
В настоящее время даже людям, далеким от науки, хорошо известно по многочисленным новостям и публикациям в СМИ, что значения так называемых глобальных финансовых индексов (например, индекса Доу Джонса), цены акций меняются хаотически. Л. Башелье предпринял первую попытку описать с использованием математики эволюцию стоимости акций. Его стохастический метод опирается на теорию вероятностей. Диссертация Л. Башелье, где представлена эта попытка, была опубликована в 1900 году. Ученый доказал формулу, известную в настоящее время как формула справедливой стоимости опциона-колл. В ней отражается стохастическая вероятность.
Важные идеи, которые в дальнейшем привели к возникновению теории эффективного рынка, были изложены в труде М. Кендалла, изданном в 1953 году. В этой работе рассматривается вопрос динамики цен акций. Исследователь описывает ее с помощью стохастических процессов.
Стохастичность в физике
Благодаря физикам Э. Ферми, С. Уламу, Н. Метрополису и Д. Нейману большое распространение получил метод Монте-Карло. Его название произошло от казино, расположенного в одноименном городе такой страны, как Монако. Именно здесь занимал деньги для игры дядя Улама. Использование природы повторов и случайностей для изучения процессов является аналогичным происходящей в казино деятельности.
При применении данного метода моделирования сначала происходит поиск вероятностного аналога. До этого моделирование осуществлялось в противоположном направлении: оно использовалось для проверки результата детерминированной проблемы, полученной ранее. И хотя и до открытия метода Монте-Карло существовали подобные подходы, они не были популярными и общими.
Энрико Ферми в 1930 году применил стохастические приемы для расчета свойств нейтрона, в то время только что обнаруженного. Методы Монте-Карло в дальнейшем использовались при работе над манхэттенским проектом, хотя в то время были существенно ограничены возможности вычислительных машин. По этой причине они получили широкое распространение только после того, как появились компьютеры.
Стохастические сигналы
Регулярные и стохастические сигналы имеют разные формы колебаний. Если повторно измерить последние, мы получим колебания, имеющие новую форму, которая отлична от предыдущей, однако проявляет определенное сходство в существенных чертах. Пример стохастического сигнала – запись колебаний волн моря.
Почему же вообще необходимо вести речь об этих достаточно необычных сигналах? Дело в том, что при изучении автоматических систем они встречаются даже чаще, чем предсказуемые.
Стохастичность и искусственный интеллект
Стохастические программы в сфере искусственного интеллекта работают с применением вероятностных методов. В качестве примера можно привести такие алгоритмы, как стохастическая оптимизация или нейронные сети. Это же относится к имитации отжига и генетическим алгоритмам. Во всех этих случаях стохастичность может содержаться в проблеме как таковой или же в планировании чего-либо в условии неопределенности. Детерминированное окружение для агента моделирования является более простым, чем стохастическое.
Итак, как мы видим, интересующее нас понятие используется во многих областях науки. Мы перечислили и охарактеризовали лишь основные сферы его применения. Изучение всех этих процессов, согласитесь, очень важно и актуально. Именно поэтому интересующее нас понятие, вероятно, будет еще долго использоваться в науке.
Вопросы по лекции 6 Концепция стохастического воздействия (продолжение) Квантовые состояния
ВОПРОСЫ по лекции 6
Концепция стохастического воздействия (продолжение)
Для моделирования какой системы вводится модель «состояние»? В каких случаях характеристики объекта становятся случайными величинами? Что такое флуктуации? Чем обусловлено возникновение флуктуаций? Чем флуктуации отличаются от погрешности? В чем состоит отличие регулируемых воздействий от стохастических? Какие типы стохастических воздействий рассматриваются в физике? Перечислите основные особенности стохастических воздействий. При каких условиях возникает квантовое состояние? Что такое квантон? О чем свидетельствует дифракция микрообъектов? Что является подтверждением утверждения о том, что дифракция наблюдается лишь на ансамбле микрообъектов. Что такое волна де Бройля? От чего зависят ее характеристики? Как проявляется влияние стохастического воздействия на величину этой характеристики? Что такое принцип суперпозиции состояний? Как на его основе разрешается парадокс с котом Шредингера? Что такое спин? Различие бозонов и формионов Почему существуют кварки разного цвета? В чем различие моделей атома по Томсону и Резерфорду? Почему необходимо усовершенствовать модель Резерфорда? Модель атома Бора и ее недостаточность В чем отличие современной модели атома от атома Бора? Как работает принцип Паули в многоэлектронных атомах? Что такое обменное взаимодействие и когда оно создает устойчивую структуру молекулы? Когда возникают у и р связи в молекулах?
Презентация была опубликована 8 лет назад пользователемweb-local.rudn.ru
Похожие презентации
Презентация на тему: » 1 Раздел 3. Концепции неклассической версии ЕНКМ 1. введение в неклассические представления Презентация 08. КОНЦЕПЦИЯ СТОХАСТИЧЕСКОГО ВОЗДЕЙСТВИЯ.» — Транскрипт:
1 1 Раздел 3. Концепции неклассической версии ЕНКМ 1. введение в неклассические представления Презентация 08. КОНЦЕПЦИЯ СТОХАСТИЧЕСКОГО ВОЗДЕЙСТВИЯ
2 2 Итак, к началу 20 века 1.В естествознании существовало значительное количество экспериментальных фактов, свидетельствовавших о значимости СЛУЧАЙНЫХ ПРОЦЕССОВ в живой и неживой природе;
3 3 Случайность в быту В быту – полная неожиданность Синонимы – непредвиденность, беспричинность, нечаянность, непреднамеренность, неповторимость.. Понятие относится к единичному событию
4 4 Случайность в науке В науке НЕ РАССМАТРИВАЮТСЯ ЕДИНИЧНЫЕ СОБЫТИЯ Einmal ist keinmal: Однажды – значит никогда! В науке случайность – хаотическое поведение многократно повторяемых событий Оборотной стороной случайности однотипных событий является вероятностное ожидание результата или прогноз.
5 5 Случайные события в природе Радиоактивный распад ядра атома –СЛУЧАЕН. Характеристика- СРЕДНЕЕ ВРЕМЯ ЖИЗНИ Хаотическое движение частиц газа – СЛУЧАЙНОЕ РАСПРЕДЕЛЕНИЕ КООРДИНАТ И СКОРОСТЕЙ Нельзя однозначно точно предвидеть момент распада ядра, значение скорости и координаты определенной молекулы газа
6 6 СЛУЧАЙНОСТЬ И ХАОТИЧНОСТЬ Явление турбулентности Процесс развития хаотичности в потоке жидкости, обтекающей тело, сопровождается каскадом случайных событий
7 7 Турбулентность и ее последствия
8 8 Неустойчивость плазмы Процессы в солнечной плазме – каскад случайных событий
9 9 Ухудшение качества прогноза со временем в сложных системах Точность прогнозирования падает со временем Мерой качества прогноза является средний квадрат ошибки Ширина кривой – границы точности прогноза Прогноз задает лишь тенденцию возникновения события, или его вероятность
11 11 прошлоенастоящеебудущее Событие Точно известно Событие имеет однозначную историю и определенное поведение в будущем Определенно, но зависит от скорости наблюдателя Определенно на основе точного знания настоящего Мир с классических позиций Мы можем точно восстановить причину события, т.е. узнать событие, предшествовавшее данному. Пример. По заданной траектории движения можно указать, через какие пункты проследовал объект прежде, чем оказался в пункте А, и где окажется (и не окажется) через некоторое время.
12 12 прошлоенастоящеебудущее Неопределенно Неопределенно Неопределенно необходимо провести опыт поведение случайно, однозначный прогноз невозможен В ситуации, когда буриданов осел уже сыт, мы не можем определить, из какой охапки он съел сено: левой, правой, или обеих вместе. Кроме того, мы не знаем, когда он снова проголодается! Мир с НЕклассических позиций
13 13 Неклассический мир Однозначно восстановить причину события невозможно, т.е. нельзя точно узнать событие, предшествовавшее данному. Понятие точной траектории отсутствует. Мы не можем указать, через какие пункты проследовал объект прежде, чем оказался в пункте А, и не можем точно определить его будущее поведение. Его движение случайно.
14 14 Особенность неклассической версии ЕНКМ Отказ от принципа однозначной и неизбежной предопределенности события Ему на смену приходит принцип неопределенности- может наступить какое-угодно событие из числа допустимых, т.е. таких, которые уже когда-то происходили или в принципе могут быть реализованы в данных условиях Событие и его характеристики приобретают случайный характер Однако это не значит, что в природе существует полная непредсказуемость события. Из всех допустимых возможностей мы ожидаем наиболее вероятную. Формируется идея неопределенности
15 15 Окружение очень велико, состоит из множества фрагментов (деталей) и оказывает беспорядочное влияние на объект Объект очень «чувствителен» к слабым воздействиям (условным толчкам со стороны окружения) Отчего происходят случайные события?
17 17 2. Концепция стохастического (нерегулярного) воздействия
18 18 Особенности неклассического описания природы Идея случайности события и случайного поведения характеристик объекта реализуется путем использования вероятностного описания этих и многих других процессов.
19 В чем причина разброса значений измеряемой характеристики? Она связана не с прибором, а с глубинным свойством самого объекта на уровне неклассического мира – с принципиально случайным поведением самих характеристик
20 20 Объект и окружение – моделируются совместно, «объект в оболочке». Окружение очень велико и оказывает беспорядочное влияние на объект, хотя оно может быть достаточно слабым Объект очень «чувствителен» к слабым воздействиям Как моделировать неклассические объекты? Эта модель называется состоянием
21 21 NB В рамках классики было достаточно моделировать только объекты per se, потому что окружение оказывает контролируемое воздействие, вызывающее регулярное изменение характеристик (по определенным законам). При этом окружение как фон не детализировалось, а заменялось определенными характеристиками воздействия (силой, потенциальной энергией и т.д.)
22 22 NB В неклассике принимается во внимание стохастический характер отношений между объектом и окружением, что ведет к необходимости моделировать их совместно, чтобы обосновать случайное изменение характеристик. Для этих целей вводится новая особая модель системы «объект + окружение», называемая состоянием.
23 23 СОСТОЯНИЕ это фундаментальная неклассическая модель, в которой одновременно учитываются и стохастическое воздействие окружения и реакция объекта в форме случайного поведения его характеристик.
24 24 СОСТОЯНИЕ КАК МОДЕЛЬ Влияние окружения БЕСПОРЯДОЧНОЕ = СТОХАСТИЧЕСКОЕ Реакция объекта СЛУЧАЙНЫЕ ЗНАЧЕНИЯ ХАРАКТЕРИСТИК Случайные величины характеризуются средним значением и дисперсией (диапазоном разброса).
26 26 Состояние описывается на языке вероятностей в зависимости от специфики стохастического воздействия с помощью понятий: Вероятности ; Плотности вероятности
0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.» title=»27 Холодная (Т=0 температура по Кельвину) Физический вакуум Теплая (Т>0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.» > 27 27 Холодная (Т=0 температура по Кельвину) Физический вакуум Теплая (Т>0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру. 0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.»> 0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.»> 0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.» title=»27 Холодная (Т=0 температура по Кельвину) Физический вакуум Теплая (Т>0) Термостат Квантовое воздействие Тепловое воздействие объект ЧТО МЫ ЗНАЕМ ОБ ОКРУЖЕНИИ? Это условная «оболочка», которая может иметь разную температуру.»>
28 Два типа состояний Если объект испытывает квантовое воздействие, то модель «объект+окружение» называется квантовым состоянием. Если объект испытывает тепловое воздействие, то модель «объект+окружение» называется тепловым состоянием.
30 30 КЛАССИЧЕСКОЕ можно задать формулой РАЗЛИЧИЕ воздействий НЕКЛАССИЧЕСКОЕ нельзя задать формулой для силы или потенциальной энергии. Для него вводят новую характеристику – действие J, для которой можно указать только минимальное значение.
31 31 концепция СТОХАСТИЧЕСКОГО ВОЗДЕЙСТВИЯ 1.К воздействиям подобного рода относятся квантовое и тепловое воздействия, которые универсальны для всего естествознания.
32 32 2. Принципиально невозможно установить однозначно (в виде формулы) законы стохастического воздействия на объект со стороны его окружения. 3. Даже в идеальном случае это воздействие не может быть сведено к нулю или устранено вовсе.
34 34 5. Вдали от порогового значения стохастического воздействия флуктуации характеристик объекта отсутствуют, что соответствует классическим представлениям.
35 35 6. Характеристики объекта принимают случайные значения, так что их можно задавать только в виде: т.е. через средние значения и отклонения от них в данном состоянии
36 36 7. Величины флуктуаций характеристик объекта не являются произвольными, а задаются окружением объекта, т.е. определяются состоянием. 8. Однозначное прогнозирование поведения характеристик объекта в этих условиях невозможно.
37 37 ОКРУЖЕНИЕ – оболочка объекта ХОЛОДНАЯ ОБОЛОЧКА К в А нТ о В о Е воздействие ТЕПЛАЯ ОБОЛОЧКА Т е п л О в О е воздействие Фундаментальная характеристика ВОЗДЕЙСТВИЯ Ћ постоянная Планка Κ в постоянная Больцмана Тип СОСТОЯНИЯ КВАНТОВОЕ СОСТОЯНИЕ ТЕПЛОВОЕ СОСТОЯНИЕ Квантово-тепловое состояние Ћ, Κ в T=0T>0 0″>
38 38 АРХИВ Это слайды, на которые студенты не должны обращать внимания
42 42 Если известна вероятность события, можно вычислить среднее значение случайной непрерывной величины и ее дисперсию, т.е допустимый разброс значений
ДЕТЕРМИНИРОВАННОЕ, СТОХАСТИЧЕСКОЕ И ХАОТИЧЕСКОЕ
Все те процессы, с которыми мы имеем дело, можно разделить на три класса: детерминированные, стохастические и хаотические.
Детерминированные процессы предполагают полную определенность своего развития, они точно диагностируемы и полностью предсказуемы. Для таких процессов характерна однозначная зависимость между их состояниями и управляющими воздействиями, что позволяет при фиксированных внешних условиях сколь угодно точно прогнозировать их развитие. В гуманитарных науках отражением детерминизма выступает теория предопределенности, а в математике детерминизм воссоздаётся в классической теории дифференциального исчисления.
Стохастические процессы — это процессы, состояние которых связано с управляющими воздействиями не однозначным образом. В одних случаях два одинаковых воздействия могут сформировать разные состояния этих процессов, а в других – два разных воздействия влекут за собой их совершенно одинаковые состояния. Развитие этих процессов также можно прогнозировать, но с некоторой неуверенностью, выражаемой вероятностью. В экономической науке типичным примером такого процесса является рыночный процесс в периоды его стабильного (бескризисного) развития. В системе свободного рынка невозможно учесть все обстоятельства динамического взаимодействия составляющих его компонентов (фирм, предприятий, холдингов, банков) не вследствие незнания их свойств, а принципиально – ввиду связности их действий. Каждый компонент рынка ведет себя, сообразуясь с собственными интересами. Но при этом он взаимодействует с другими компонентами, корректируя их действия и подправляя свои действия по результатам взаимодействия. В итоге все участники рыночного процесса движутся в возмущенном, постоянно формирующемся экономическом пространстве по случайным траекториям. Поэтому грамотные экономисты прогнозируют развитие того или иного субъекта рыночного процесса не траекторией (трендом), а ансамблем траекторий, когда этот субъект движется как бы по нескольким траекториям сразу, но с разными вероятностями.
Хаотические процессы — это процессы, в которых имеет место не детерминированное, не стохастическое и не смешанное, а некоторое более общее поведение, которое получило название динамического хаоса. В отдельных ситуациях в этих процессах наблюдается как стохастизм, так и детерминизм, но в общем случае они не сводятся ни к одному из них, представляя, по сути, явление иного качества. Типичным примером процесса такого типа является все тот же рыночный процесс, если принять во внимание не только периоды его стабильного, но и кризисного развития. Сущность процессов хаотического типа раскрывается с помощью такого понятия как «аттрактор» (от лат. attraktio – притяжение) – точка или область пространства, к которой тяготеет траектория процесса. В частности, для процесса движения обычного маятника аттрактором является точка его равновесия. Для хаотических процессов характерны аттракторы особого типа, в которых точки притяжения никогда не повторяются и притягивающие траектории никогда не пересекают друг друга, однако эти точки и траектории неизменно остаются внутри некоторой области пространства. Их стали называть странными аттракторами. Смысл странного аттрактора в том, что им характеризуется область, где процесс становится слабоуправляемым, а его развитие — слабо предсказуемым доже при вполне определенных управлениях. Таким образом, с управленческой точки зрения в странном аттракторе нет ничего необычного — это кризис, нарушение равновесия и в то же время переход к некоторому новому равновесию.
Рассмотренная нами типология позволяет правильно подойти к вопросам прогнозирования при управлении в социальных и экономических системах. Детерминированные процессы имеют достаточно большой горизонт прогноза, соизмеримый с жизненным циклом той системы, где они развиваются. Управляя этими процессами, можно однозначно ответить на вопрос «что будет» в результате того или иного управления. Для стохастических процессов характерен такой же горизонт прогноза, как и для детерминированных процессов. Управление этими процессами осложняется тем, что нельзя однозначно сказать, «что будет» при том или ином управлении, но можно ответить на вопрос «что вероятно будет». При управлении хаотическими процессами не только нельзя сделать точный прогноз их развития на приемлемый период времени, но и проверить результаты прогноза инструментальными или какими-либо другими экспериментальными способами. Иными словами, при управлении хаотическими процессами невозможно ответить на вопросы «что будет» и «что вероятно будет», лучшее, что можно сделать — это выяснить «что может быть» и «чего не может быть». А это уже шаг вперед к осознанному управлению социальными, экономическими и иными процессами хаотического типа.
Концепция стохастического воздействия предполагает что
Стохастическое управление
Можно с самого начала формулировать задачу управления в условиях неполной информации, как задачу детерминированного управления сглаженными и экстраполированными в соответствии с теми или иными принципами процессами. Однако далеко не всегда удается разделить уже сформулированную задачу стохастического управления с заданным целевым функционалом и заданными ограничениями на две задачи на сглаживание и прогноз в соответствии с некоторыми принципами и на последующее детерминированное управление. Анализ, проведенный в гл. 14, устанавливает случаи, в которых задачи фильтрации и прогноза из достаточно широкого класса со сложными целевыми функционалами могут быть сведены к задаче сглаживания и упреждения по минимуму дисперсии. Полученные при этом результаты указывают пути выделения круга задач стохастического управления, процесс решения которых может быть конструктивно разделен на решение задачи прогноза и анализ задачи детерминированного управления. [c.44]
Общая задача стохастического управления является задачей стохастического программирования. Закон управления представляет собой решающие правила или решающие распределения. Класс допустимых структур решающих правил или решающих распределений задается заранее, исходя из специфики задачи. [c.44]
Линейный механизм функционирования системы и квадратичный целевой функционал, существенно облегчающие синтез детерминированных управляющих устройств, теряют в значительной мере свою привлекательность при переходе к стохастическому управлению. Дело в том, что вычисление вероятностных характеристик системы, с которыми обычно связано построение детерминированного эквивалента задачи, так или иначе требует ввода нелинейных операций. [c.45]
Достаточно общая модель стохастического управления представляет собой модель стохастического программирования, в которой требуется минимизировать средний риск или максимизировать среднюю полезность— математическое ожидание некоторой случайной функции от параметров состояния и, возможно, от параметров управления — при трех группах условий. Первая группа условий связывает параметры состояния в различные моменты времени с параметрами управления. Эта группа условий определяет механизм функционирования системы. Такие ограничения задаются обычно в жесткой форме. Учитывая, однако, случайные возмущения, возникающие на входе системы, и погрешности наблюдения состояний системы, может оказаться целесообразным заменить жесткие ограничения, описывающие механизм функционирования устройства, вероятностными. Вторая и третья группы условий фиксируют допустимые области определения переменных состояния и соответственно параметров управления в различные моменты времени. В зависимости от содержательных особенностей задачи эти ограничения могут быть статистическими, вероятностными или жесткими. [c.45]
Модели стохастического управления, в которых закон управления или механизм управления учитывает последовательный характер накопления информации и может уточняться в процессе управления, описываются многоэтапными стохастическими задачами. Целевой функционал динамической задачи зависит от состояния системы на конечном (.S-M) этапе или от всей траектории системы. Область определения задачи отдельного этапа описывается жесткими или условными статистическими или условными вероятностными ограничениями. Оптимальные решающие правила или решающие распределения этих задач определяют законы управления или механизмы стохастического управления. [c.46]
Обычно в качестве целевого функционала задачи принимают среднее значение функции риска или функции полезности, зависящей от траектории системы или от ее конечного состояния. Можно указать, однако, задачи, в которых любая траектория, не выходящая из некоторой заранее заданной области изменения состояний системы, является приемлемой. В таких задачах естественно принимать в качестве целевого функционала затраты (энергии или ресурсов), связанные с управлением. В общем случае критерий качества решения задач стохастического управления при неизвестных характеристиках управляемого объек- [c.49]
Ограничения k-ro этапа (t = k 2) содержат в качестве параметров условий задачи элементы матрицы А координаты вектора состояния системы для i