Координатная плоскость что первое х или у

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Прямоугольная система координат в трехмерном пространстве

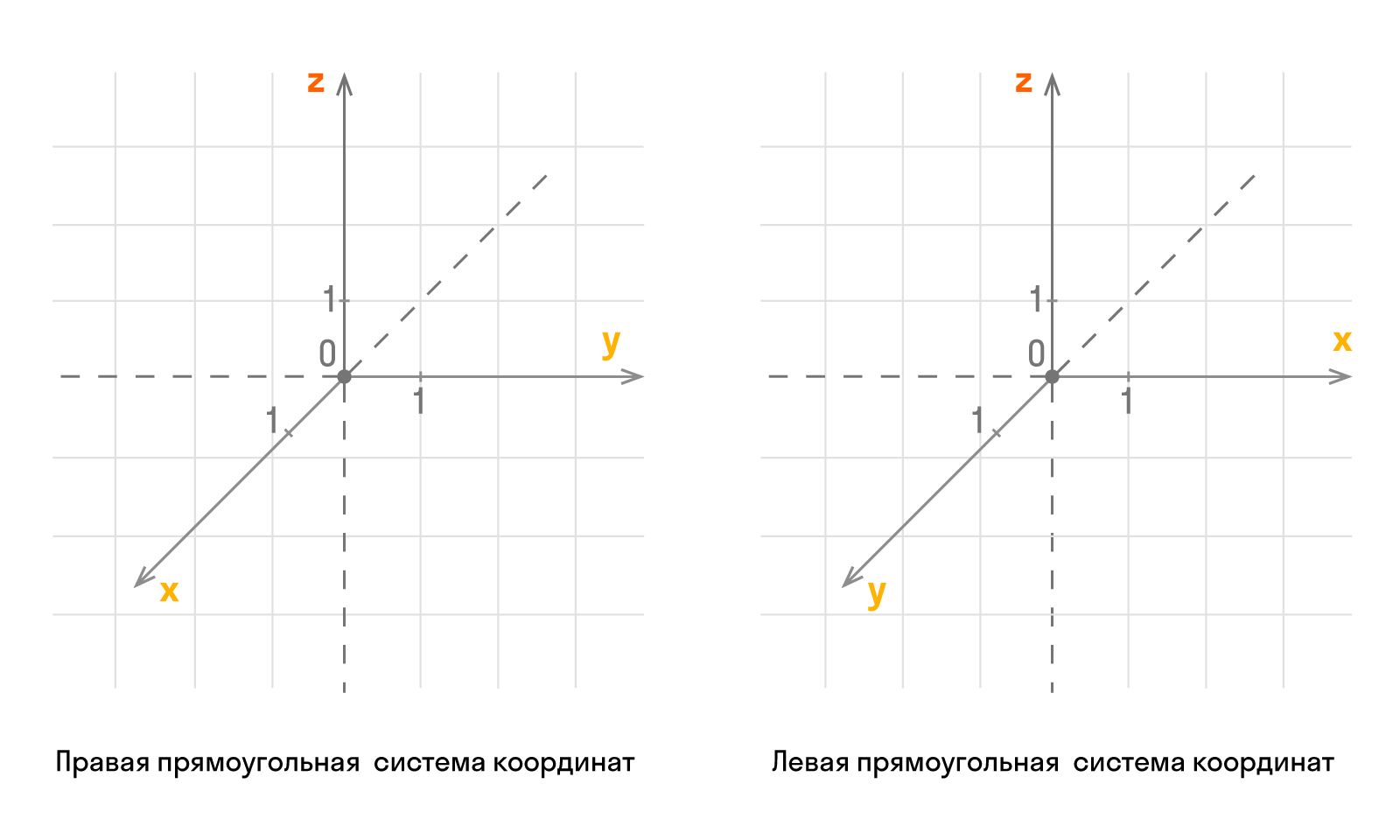
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

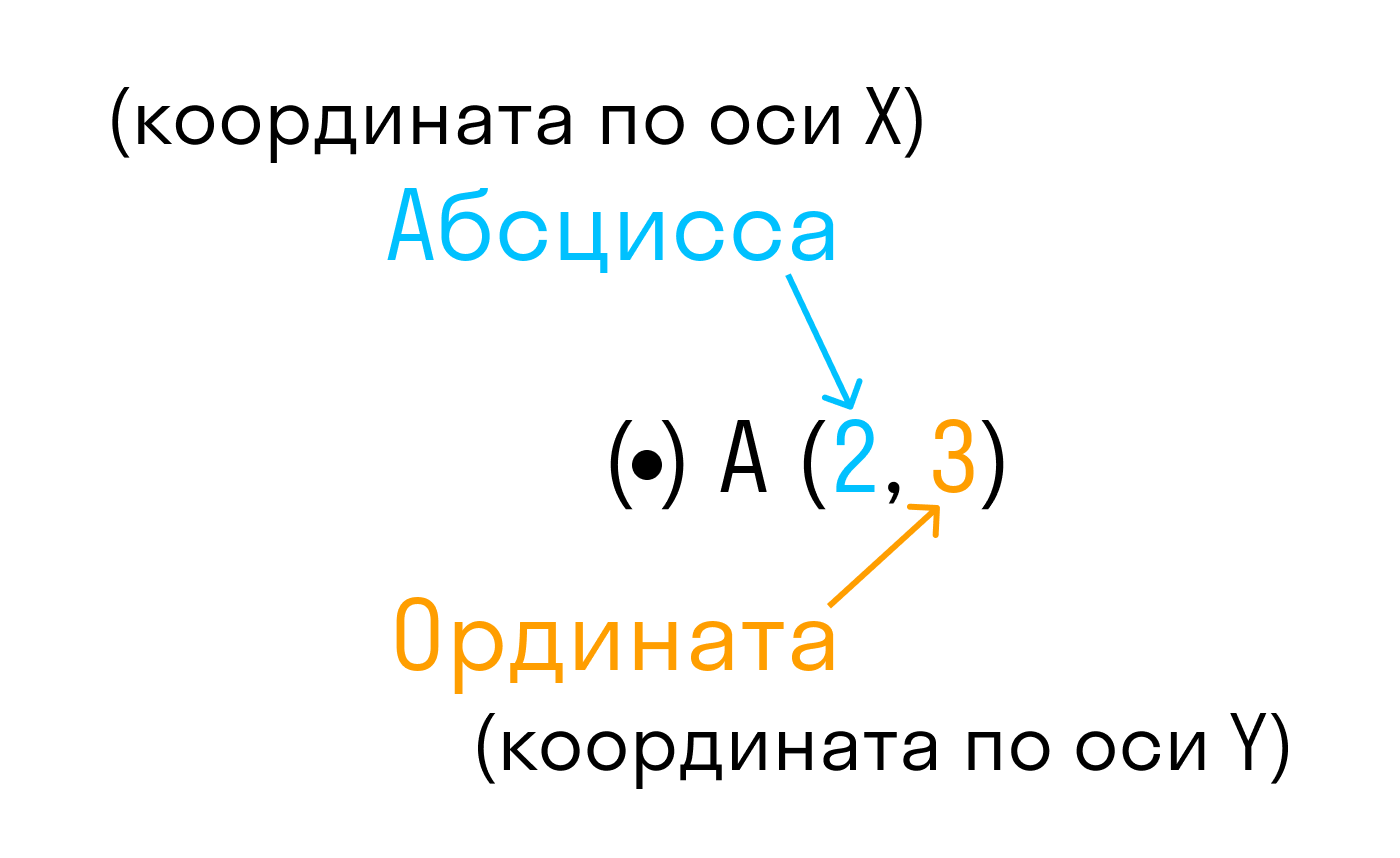
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

Сформулируем определение точки М в трехмерном пространстве.

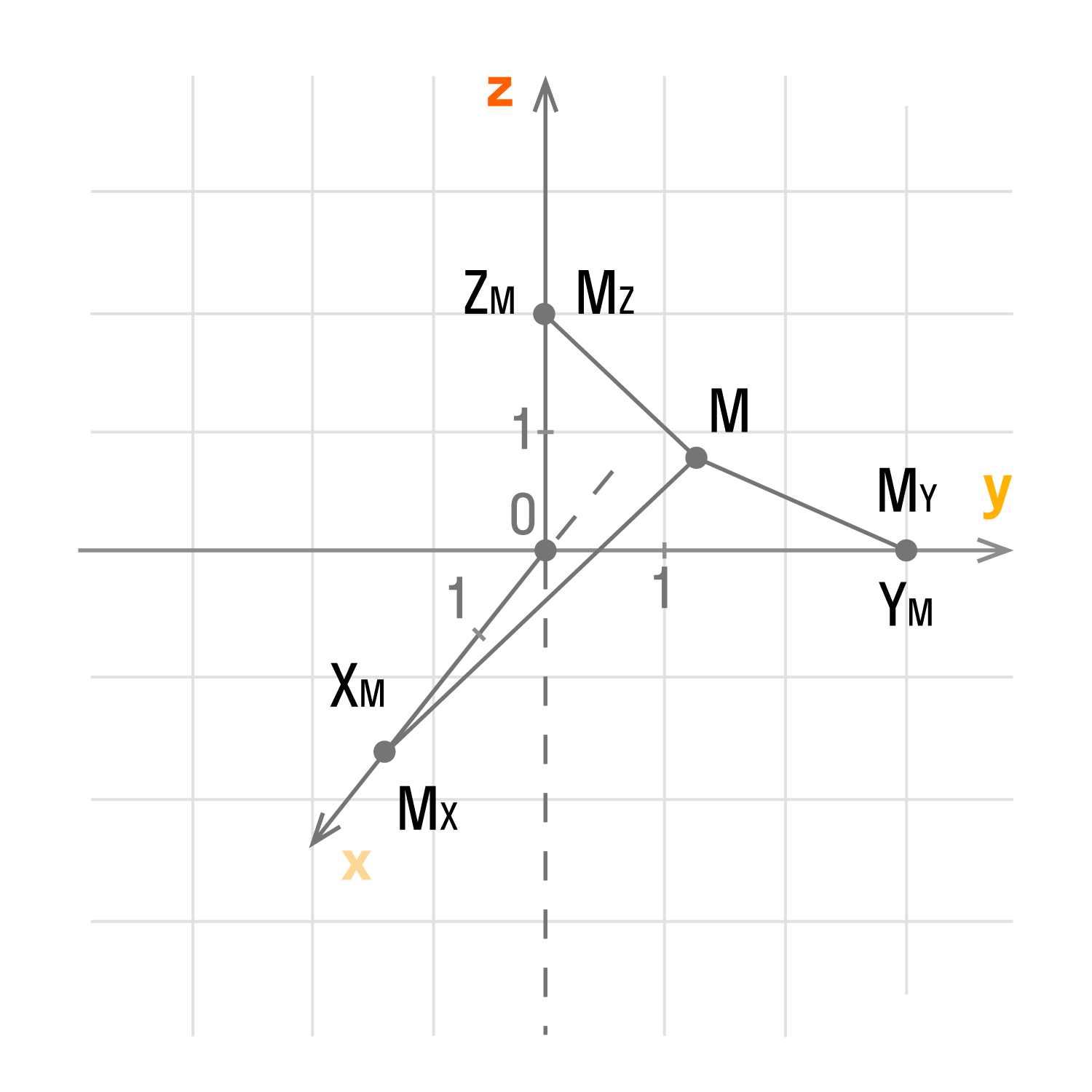
Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

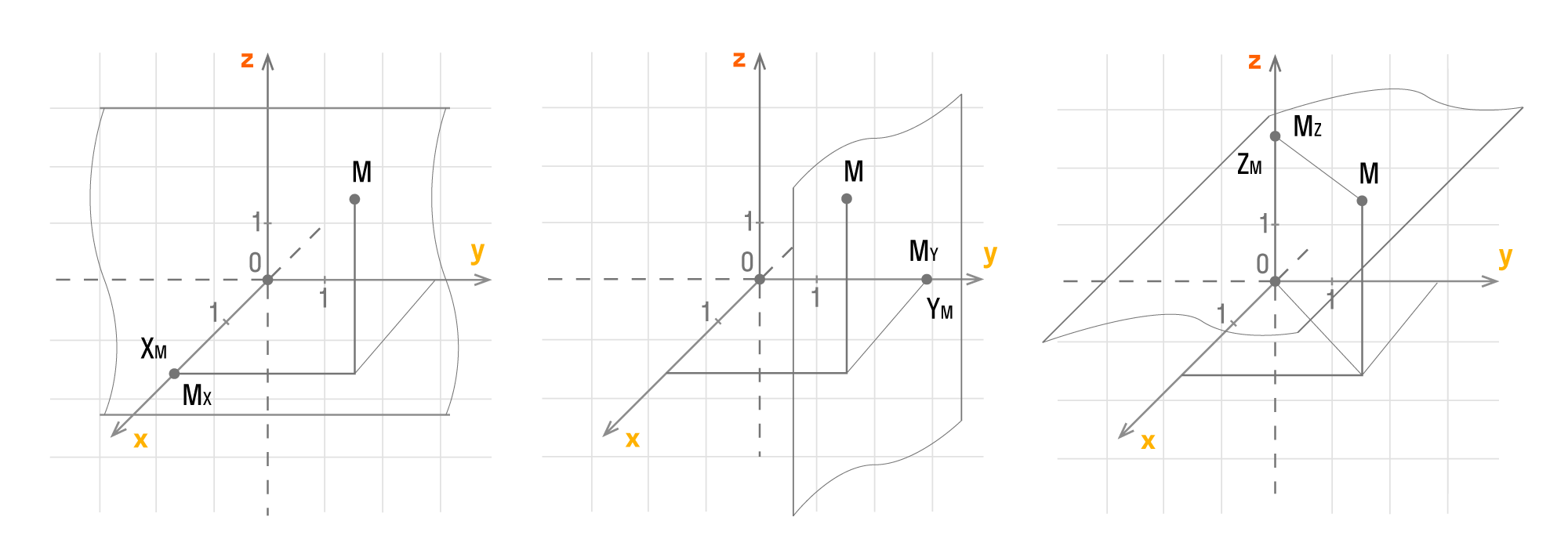
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Источник

Геометрия: координаты, фигуры

Координатная плоскость

Определение координатной плоскости

Теория

Координатная плоскость. Правила

Плоскость – это понятно. Легче объяснить, чего на плоскости нет – впадин, возвышений прогибов.

Координатная плоскость – это плоскость, на которой нарисованы две оси под прямым углом.

Второе число – проекция точки на ось Y.

Точка на координатной плоскости. Точка она совсем маленькая. Координаты точки это пара чисел, например

Координатная плоскость, квадранты

Задачи на бумаге

В каком квадранте лежит точка

Нарисовать эти точки на плоскости

Задачи найти координаты точки …

Игра – найди координаты точки.

Для этого запускаем скретч.

Улитка спрашивает: «где цель?»

Нужно правильно ввести положение точки по оси X и по оси Y внизу экрана.

Источник

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

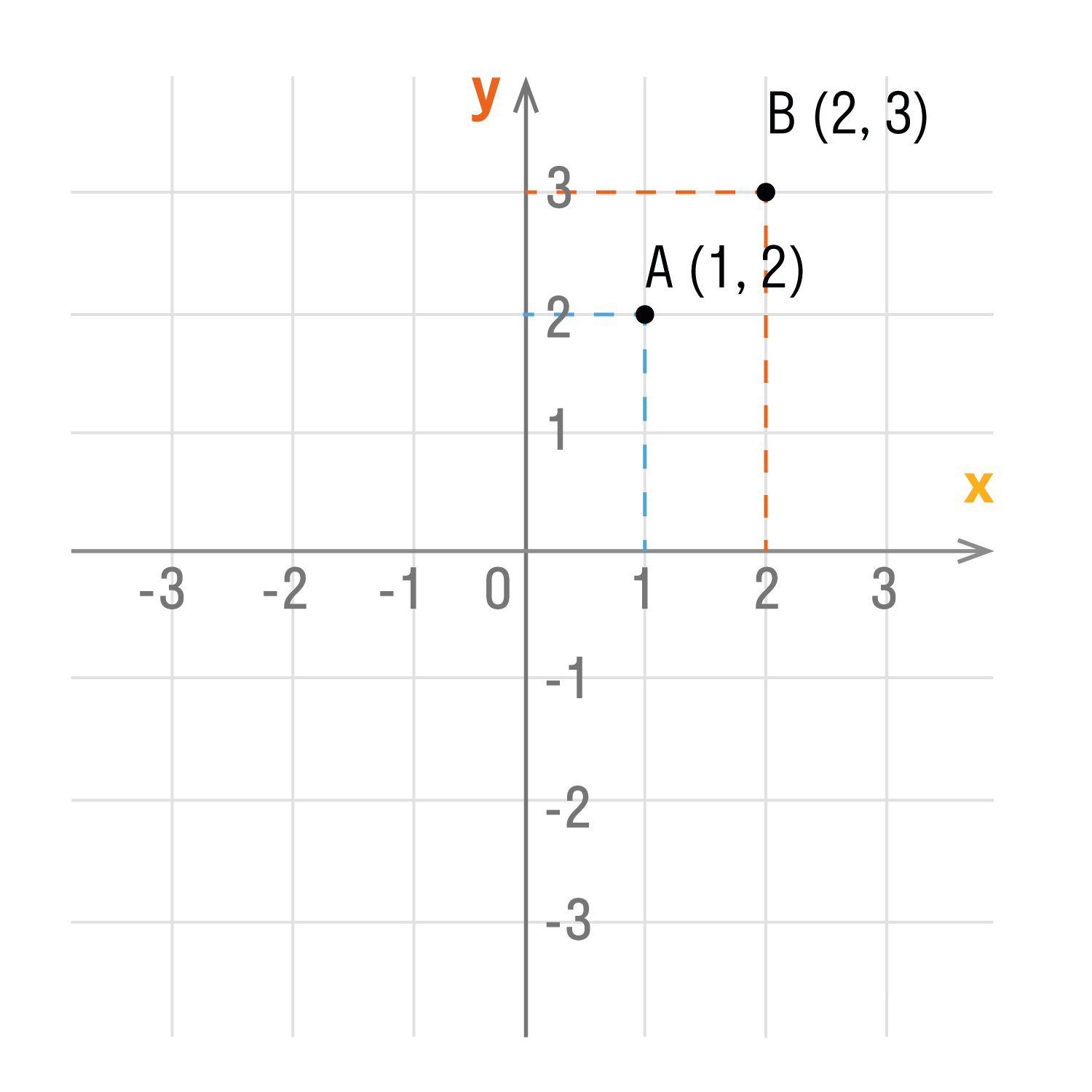
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Координаты. Декартова система координат.

Координаты – совокупность данных, на основании которых точно характеризуется местоположение объекта.

Рене Декарт (1596–1650) предложил представлять местоположение точки на плоскости при помощи пары координат.

Для характеристики координат требуются ориентиры. Данными ориентирами на плоскости выступают две числовые оси. Сначала чертят горизонтальную ось, её принято определять как ось абсцисс и подписывать буквой х, указывают, что это ось 0х. Положительное направление на оси абсцисс принято слева на право и указывается стрелкой.

Следующей чертят вертикально ось, её принято определять как ось ординат и подписывать буквой у, указывают, что это ось 0у. Положительное направление на оси ординат принято снизу вверх и указывается стрелкой.

Оси пересекаются под углом 90°, то есть являются взаимно перпендикулярными. Точку их пересечения обозначают как «0». Точку «0» принято считать исходной точкой для отсчёта по каждой из осей.

Система координат — это две взаимно перпендикулярные координатные прямые, которые пересекаются в месте, являющемся началом отсчёта для каждой из них.

Координатные оси — это прямые, формирующие систему координат.

Ось абсцисс (0x) — расположенная горизонтально ось.

Ось ординат (0y) —расположенная вертикально ось.

Координатная плоскость — плоскость, в которой сформирована система координат. Для обозначения данной плоскости применяют x0y.

Цифры, указывающие числовые значения на осях размещают как по правую, так и по левую сторону от оси 0y. Цифры на оси 0x принято указывать внизу под осью.

Чаще всего единичные отрезки по оси 0y и оси 0x одинаковы. Но встречаются ситуации, когда они не равны друг другу.

Оси координат разделяют плоскость на 4 угла, которые обозначают как координатные четверти. Четверть, сформированная положительными полуосями (правый верхний угол), принято считать первой (I). Остальные четверти (координатные углы) располагаем против часовой стрелки.

Источник

Урок 46 Бесплатно Координатная плоскость

До этого занятия мы обсуждали с вами только прямую и все, что с ней связано.

Сегодня урок посвятим изучению плоскости.

Узнаем, что называют координатной плоскостью и как получить её из обычной плоскости.

Познакомимся с прямоугольной системой координат на плоскости и разберем ее основные характеристики и особенности.

Выясним области применения и использования систем координат в практических целях и в жизни человека.

Научимся пользоваться прямоугольной системой координат на плоскости: определять координаты заданных точек и по заданным координатам точки находить ее положение на координатной плоскости.

Координатная плоскость и ее основные особенности

Представим движение автомобиля по прямолинейному участку дороги.

Любой прямолинейный участок дороги легко представить с помощью координатной прямой.

Координатная прямая позволяет нам связать точки на этой прямой с числом.

Вам уже известно, как из любой прямой получить координатную прямую.

Необходимо на прямой выбрать начало отсчета, задать направление и единичный отрезок (масштаб).

В результате с помощью координатной прямой вы однозначно определите, что конкретной точке на прямой соответствует ее единственное верное значение с соответствующим знаком.

И наоборот, если известна координата точки, то можно определить положение этой точки на координатной прямой.

Таким образом, для указания местоположения точки (в нашем случае автомобиля) на прямой нужна только одна координата на координатной оси.

В жизни часто приходится устанавливать положение точки по нескольким параметрам. В таком случае для однозначного определения положения точки требуется больше информации.

Предположим, купили мы билет на концерт.

Чтобы определить расположение конкретного кресла в зале, в билете указывают адрес места: номер ряда и номер кресла в ряду.

Так как каждому месту ставится в соответствие два числа, то для однозначного определения положения точки нам не будет хватать одной координатной прямой.

Для обозначения числами точного положения точки на плоскости используют математическую модель, которую называют координатной плоскостью.

Чтобы из обычной плоскости получить координатную, необходимо на этой плоскости задать определенную систему координат.

Существует различные системы координат.

Мы рассмотрим прямоугольную систему координат на плоскости.

Прямоугольной системой координат на плоскости называют систему из двух взаимно перпендикулярных прямых с общим началом отсчета и общей масштабной единицей.

Рассмотрим основные составляющие прямоугольной системы координат.

Единичный отрезок выбирается чаще всего одинаковый для каждой координатной оси.

Направление осей указывается стрелкой, каждая ось подписывается буквой.

Для координатных осей обычно выбирают положительное направление, т.е. «по умолчанию» принято использовать правостороннюю систему координат, в которой за положительное направление осей принимают ось ординат, направленную вверх, и ось абсцисс, направленную вправо.

Если приходится по каким-либо причинам использовать левостороннюю прямоугольную систему координат, то данный факт оговаривают в задаче.

Положение точки на плоскости определяется двумя упорядоченными числами: координатами х и y.

Координату точки на плоскости записывают так:

Например, координата точки A:

A(2;-1), где

У меня есть дополнительная информация к этой части урока!

Чтобы запомнить порядок следования абсциссы и ординаты в записи координаты точки, часто используют такое сравнение:

Представьте, многоэтажный дом, а в нем вашу квартиру.

Чтобы попасть домой, первым делом вам необходимо зайти в нужный подъезд (координата по оси Ох), а затем подняться на нужный этаж (координата по оси Оу).

Координаты могут иметь различные числовые значения, в том числе быть равными нулю.

Если ордината точки равна нулю, то точка лежит на оси Ох.

Если абсцисса точки равна нулю, то точка лежит на оси Оу.

Нумерация координатных плоскостей ведется против часовой стрелки римскими цифрами I, II, III, IV.

Если точка имеет положительную координату х (х > 0) и положительную координату у (у > 0), то она лежит в I координатной четверти.

Если точка имеет отрицательную координату х (х 0), то она лежит во II координатной четверти.

Античные ученые, мыслители (астрономы, философы, географы) на протяжении нескольких столетий пытались создать теорию о происхождении окружающего мира и всего мироздания в целом, изобразить известные им моря, океаны, страны в чертежах, а звездное небо на карте.

Благодаря великим умам появилось огромное множество фундаментальных знаний, понятий, представлений.

Появилось представление о Земле как о шаре, о ее расположение на звездном небе; создавались все более совершенные карты и планы, методы определения географических координат; на карту наносились линии широты и долготы, сетка параллелей и меридиан.

Долгое время лишь география и астрономия пользовались данными знаниями.

В XIV веке французский философ, астроном, математик Никола Орем пытался применить метод координат к геометрии.

Одной из самых важных математических работ Орема стал «Трактат о конфигурации качеств».

Именно в этой работе он ввел графическое изображение зависимости одной величины от другой с помощью прямоугольной системы координат, называя широтой и долготой то, что сейчас называют абсциссой и ординатой.

Это нововведение стало отправной точкой создания современного метода координат.

Научному обоснованию прямоугольной системы координат мы обязаны французскому ученому, философу Рене Декарту.

Он обобщил известные на то время знания по этой теме и дал научное истолкование прямоугольной системе координат.

Предложенная им прямоугольная система координат получила его имя, ее стали называть декартовой системой координат.

Координатный метод описания геометрических объектов положил начало аналитической геометрии.

Создание аналитической геометрии позволило переводить геометрические свойства тел и кривых на алгебраический язык, вместо геометрических построений использовать расчеты; кроме того, стало возможным анализировать геометрические объекты с помощью уравнений.

Развитием координатного метода и аналитической геометрии занимался также современник Рене Декарта, знаменитый французский ученый Пьер Ферма.

Однако все научные труды Ферма были опубликованы только после его смерти

Пройти тест и получить оценку можно после входа или регистрации

Источник