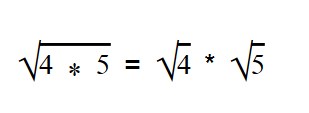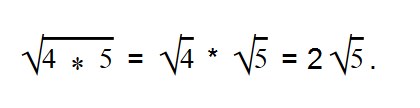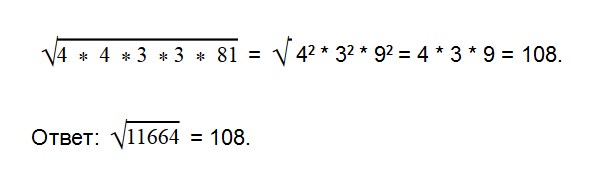Корень это что такое 4 класс
Корень и однокоренные (родственные) слова
Корень может состоять из одной, двух и более букв:
Б ить, л ить, пь ю, икр а, мел ок, снеж инка, баран
В слове может быть, как один корень, так и несколько (два и более).
Слова с несколькими корнями называют сложными.
Чтобы найти корень в слове, надо подобрать к нему однокоренные слова, общая часть этих слов и будет корнем.
лент очка ( лент а, лент очный)
под вяз ка (за вяз ать, с вяз ка)
красн ый ( красн ота, пре красн ый)
Однокоренные слова
Корень является общей частью однокоренных или родственных слов, в нем заключено их общее значение.
Корень в родственных словах обычно одинаков для всех слов:
Сказ ание, рас сказ ывать, сказ очно
Однако может быть чередование согласных букв в конце корня или чередование гласных букв в корне:
Книг а – книж ный, зар я – зо́р и
Помни, что в родственных словах корень обязательно должен быть одинаковым не только по форме (составу букв), но и по смыслу, который он несет!
Не путай однокоренные слова и формы одного и того же слова!
Однокоренные слова меняются с помощью приставок и суффиксов, тогда как в формах слова изменяется только окончание!
Поделись с друзьями в социальных сетях:
Что такое корень слова?
Корень слова — это его главная значимая часть, в которой заключено общее значение всех однокоренных слов.
Корень — главная морфема
Как главная морфема, корень объединяет слова по общности их значения, например:
вод ный — под вод ный — вод яной — вод ник — под вод ник — вод янистый.
Все эти слова обозначают предметы или признаки, имеющие отношения к водной стихии, так как в их морфемном составе прослеживается один и тот же корень вод-.
В слове может быть один или два корня
вод ный — вод о лаз — вод ос брос — вод о хран илище.
Следует различать слова с совпадающими по звучанию и написанию корнями, но разными по значению:
В морфемном составе этих слов вычленим корень гор-, но это не один и тот же корень, а разные морфемы, не совпадающие по своему лексическому значению.
Корень в составе различных слов
Слов, состоящих из одного корня и окончания, в русском языке насчитывается немного, например:
вод а, сел о, пол е, земл я, неб о, юн ый, бел ый, зелён ый, перв ый, пят ый, вед у, нес у, ид у.
Корни этих слов способны выступать без приставок и словообразовательных суффиксов, поэтому их называют свободными.
Большинство слов русского языка состоят из сочетания разных морфем:
1. корня, суффикса, окончания
3. приставки, корня, суффикса, окончания
4. приставки, корня, суффикса, суффикса
Некоторые корни в свободном виде не встречаются. Они являются связанными с приставками, суффиксами или с другими корнями:
Как определить корень в слове?
Чтобы определить корень в слове, подбираем родственные слова и вычленяем в них общую значимую часть, в которой содержится их основное лексическое значение, например:
лес — лес ной — лес ник- лес ничий — лес ничество;
Общей частью этого ряда однокоренных слов является часть лес-, которую назовем корнем.
Трав а — трав ка, трав инка, трав ушка, трав яной, за трав енеть.
Главной морфемой этого ряда родственных слов является часть трав-, которую выделим в качестве корня.
Видео «Корень слова. Однокоренные слова. Написание корня в однокоренных словах»
Корень слова

Всего получено оценок: 291.
Всего получено оценок: 291.
В богатом русском языке, оказывается, не так много корней – всего четыре с половиной тысячи, от которых образуются все остальные слова. Корень – это путеводный огонек, который приводит к пониманию того, что значит слово, и помогает объединить его в группы со словами, у которых такой же корень. Именно поэтому так важно изучить данную тему русского языка 4 класса.
Что такое корень слова?
Это его главная часть, которая является носителем значения. Таким образом, если у нескольких разных на первый взгляд слов один корень, то и значение у них будет похожим. Такие слова называются однокоренными. Получается, что корень нужен не только для того, чтобы нести в себе значение слова, но и для того, чтобы объединять слова, которые могут относиться к разным частям речи, в общую лексическую группу.
У всех корней есть один общий секрет – они пишутся одинаково.
Как в слове найти корень?
Сделать это не так просто, как может показаться – и одним словом тут не обойдешься. Нужно найти несколько похожих на него слов и выделить в них общую часть. Это и будет корень.
Родственные слова также можно узнать по описанию их значения – во всех описаниях будет в том или ином виде присутствовать значение, заключенное в корне. Например, снеговик – это слепленная из снега фигура, а снегоход – это машина, которая нужна для передвижения по снегу. Они связаны общем корнем “снег” и значением.
Иногда можно ошибиться и отнести к родственной группе слова с одним корнем и разными значениями. Дело в том, что в русском языке есть корни, которые пишутся совершенно одинаково, но имеют разное значение. Например, корень реч – на первый взгляд объединяет слова речка и речь, но на самом деле они не являются родственными.
Как правильно писать корень слова
Правописание корня слова регулируется несколькими очень важными правилами.
Первое говорит, что если в корне есть безударная гласная, то ее нужно проверить, подобрав слово с таким же корнем, где она стояло бы под ударением. Например, слово лесник проверяется с помощью однокоренного лес.
Также важно помнить, что есть слова, в которых буквы в корне могут чередоваться, при этом они все равно остаются однокоренными. Правописание таких корней будет зависеть от ударной/безударной позиции или от суффикса, который за ними следует.
В русском языке также есть много слов, где правописание корня нельзя просто проверить – они называются словарными, и их следует запомнить.
Что мы узнали?
Корень слова – это та его часть, в которой заключено его значение. В русском языке есть слова с одним и тем же корнем – они называются однокоренными, а также родственными. Правописание корней определяется несколькими правилами: безударную гласную в коре можно проверить, поставив ее в ударное положение, иногда они чередуются, и это чередование зависит от того, использован после корня суффикс или нет, а также от того, в ударном или безударном положении находится корень. Некоторые слова имеют корни, не подчиняющиеся правилам – они называются словарными и их написание нужно просто запомнить.
Корень слова – что это такое, как его правильно выделить в слове и что про него обязательно надо знать
Наименьшая значимая часть слова.
Вы открываете учебник и там написано, что корень – это наименьшая значимая часть слова. И что? Как вы это понимаете? В другом учебнике написано, что в корнях слов заключается их лексическое значение. А это как понять?
Вы, может быть, еще поймете, а ваш ребенок, который в начальной школе – нет. Давайте разбираться.
Что значит «наименьшая значимая часть слова»
Поясняю сразу на примере. Что значит «л»? Ничего. Ничего у вас в голове не рисуется. Что значит «ле»? Ничего. Что значит «лес»? Опа! Сразу в голове «вспыхивает» картинка – сразу вы видите высокие сосны, плотные стволы деревьев, короче, видите лес.
Вот и получается, что «лес» – вот эти самые три буквы – наименьшая часть слова, которая что-то ЗНАЧИТ, то есть она «значимая», то есть в ней заключается лексическое значение слова, то есть вы представляете себе что-то, когда слышите/читаете эти три буквы.
Это слово можно «увеличивать», добавляя к нему:
Но «наименьшая» часть, которая связывает все слова, все равно будет «лес».
Вот эта наименьшая часть – корень.
Как найти корень слова
Есть две стратегии. Самая популярная – подбирать однокоренные слова. То, что не будет меняться, будет корнем. Например, надо вам определить корень в слове «подводник». Подбираем однокоренные: подводный, водный, вода. Корень – «вод».
Другая стратегия. Надо отделять буквы от корня и смотреть, теряется лексическое значение или нет. Например, разбираете вы слово «почка». И что-то затупили и задумались – «почк» или «поч»? Надо подумать, сохраняется ли лексическое значение у букв «поч». Нет. Буква, которая следует за «ч» тоже входит в корень, потому что она полностью меняет значение. Сравните:
80 % слов вы сможете разобрать, пользуясь этими двумя стратегиями. Но русский язык коварен и сложен, поэтому надо помнить еще кое о чем.
У корней должно быть одинаковое лексическое значение
Это самый важный принцип. Почему мы выделили корень «лес» в словах «лесник», «подлесок», «лесной», «лесничество»? Потому что они все связаны с лесом. А вот два других примера.
«Богатство». Ученик начинает разбирать и думает: «Хм. Какой же тут корень: богат или бог»? Действительно, вопрос интересный. Я даже слышал выражение такое: «Богатство от слова Бог, а нищета от слова «не считать». И как же разобрать?
Кто такой Бог? Это Всевышний. Когда мы говорим это слово мы представляем кого-то, кто, скажем так, находится на небе. А что такое богатство? Деньги, золото, драгоценности, роскошные особняки.
Как они связаны? Никак. Значит, надо выделять корень «богат», а не «бог».
Слову «бог» примерно столько же лет, сколько словам «мать» и «отец». Но оно раньше обозначало обычного человека. Человека, который кому-то что-то отдал. Вот я дам деньги нищему, я для него – «бог».
От этого существительного образовалось прилагательное «богатый» – тот, кому «богом» (= человеком) многое дано. В нем был корень «бог» и суффикс «ат».
Когда переводили библейские тексты, возникла проблема. Там было нарицательное существительное, которое обозначало Всевышнего. А в славянских языках такого существительного не было. Ну просто вот не было и всё.
И стали думать, как быть. И взяли для перевода два слова: «господь» = «господин» и «бог» = «податель благ».
Прошло какое-то время и первое значение у слова «бог» забылось. «Бог» стал именно «Всевышним», Творцом.
Связь между словами «бог» и «богатый» разорвалась. Они в современном русском языке никак не связаны. Поэтому мы и выделяем корень «богат», а не «бог».
То же самое со словом «работа». Раньше работа была уделом рабов, но сейчас ведь рабства уже нет. А работа есть. Работать могут творческие люди, работают бизнесмены, политики. Связь с «рабами» разорвалась. Поэтому мы выделяем в этом слове корень «работ», а не «раб».
Однокоренные слова и формы слов – в чем разница
У форм слов и у однокоренных одинаковые корни. Но у однокоренных слов разные приставки или разные суффиксы, а формы отличаются только окончаниями. Сравните:
Если говорить более научно, то у однокоренных слов немного разные лексические значения, а у форм слов лексические значения одинаковые, но разные грамматические значения. Грамматическое значение – это информация о роде, числе, падеже.
Обратите внимание, глагол без суффикса «л» и с суффиксом «л» – это формы одного и того же слова. Потому что значение у них не меняется ни на йоту, меняется только грамматический признак – время: делаю (настоящее), делал (прошедшее). Но сам глагол-то не изменился.
А вот если к нему добавить приставку: сделал – то это уже будет однокоренное слово. Потому что делать – это какое-то продолжительное действие, а сделать – законченное действие. Сделал = довел до конца.
Как проверять орфограммы в корнях
Мы можем сомневаться в написании гласных и согласных в корнях. Чтобы проверить согласные, надо подбирать однокоренные слова или формы слов. В слове «дуб» на конце пишется «б», потому что его можно проверить формой «дубы» или однокоренным «дубок». В слове «здравствуйте» пишется «в», потому что оно от «здравия». В «вестнике» пишется «т», потому что оно от существительного «весть».
Иногда согласную проверить нельзя. Тогда надо смотреть в словарь. Например, почему в прилагательном «абсолютный» пишется «б», а не «п»? Потому что в словаре так написано. Проверить эту букву нельзя.
Гласные в корнях либо также проверяются подбором однокоренных слов и форм (мести – мёл, везти – вёз), либо запоминанием (собака – букву «о» невозможно проверить).
Но. В корнях бывают еще чередующиеся гласные. Например, в слове «замирать» мы пишем «и», потому что после корня есть «а». А вот «замереть» пишется с «е», потому что после корня нет «а».
Корни с чередованием надо запомнить.
Полезные материалы по теме
Подпишитесь на рассылку сайта. Я еженедельно буду высылать вам наши лучшие статьи из рубрики Образование. Рубрика будет продолжать развиваться, скоро появятся тексты по математике, биологии и другим школьным предметам.
Посмотрите мои статьи с курсами подготовки к ЕГЭ, ВПР и ОГЭ. На курсах преподают лучшие учителя, многие из них сами являются экспертами ЕГЭ. Курсы помогают системно готовиться ко всем видам контроля, а стоят часто дешевле, чем репетиторство.
Не поленитесь и посмотрите вот это трехминутное видео о том, как объяснять орфограммы. Если вы будете правильно их объяснять все 11 лет обучения в школе – у вас никогда не будет проблем с грамотностью. Я объяснял именно так и никогда не ходил к репетиторам по русскому. Когда поступал на филфак, был первым по количеству баллов.
Уважаемые читатели, напишите, пожалуйста, комментарий к статье. Скажите мне, сумел ли я вам объяснить, что такое корень, были ли мои советы и примеры полезны. Если текст вам не нравится, если его сложно читать, – критикуйте смело, буду править.
Что такое квадратный корень
Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
Это два нетождественных друг другу выражения.
Из выражения x 2 = 16 следует, что:
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
Ищем в таблице число 7396.
Ищем в таблице число 9025.
Ищем в таблице число 1600.
Извлечением корня называется нахождение его значение.
Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
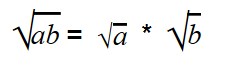 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
Деление арифметических корней
Для деления арифметических корней используйте формулу:
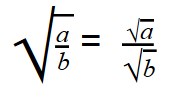 |
Примеры:
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
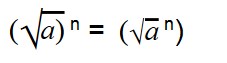 |
Примеры:
Эти две формулы нужно запомнить:
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
109004, Москва, ул. Александра Солженицына, 23а, строение 1, подъезд 10