Корреляция и регрессия в чем разница
Отличия между регрессионным и корреляционным анализом.



Задачей регрессионного анализа является построение зависимости математического ожидания одной или нескольких случайных величин от одной или нескольких неслучайных величин.
Хотя вычисления в регрессионном и корреляционном анализах весьма схожи, между этими методами есть существенная разница. Неслучайность в регрессионном анализе означает измерение без ошибок (с абсолютной точностью). В корреляционном анализе в «случайность» исследуемых величин могут входить ошибки измерений. Использование методов корреляционного и регрессионного анализов требует выполнения определенных предпосылок.
• Связь как синхронность (согласованность) – корреляционный анализ.
• Связь как зависимость (влияние) – регрессионный анализ (причинно-следственные связи).
Сравнение коэффициентов корреляции и регрессии
• Показывает силу связи между признаками
• Знак коэффициента говорит о направлении связи
• Может принимать любые значения
• Привязан к единицам измерения обоих признаков
• Показывает структуру связи между признаками
• Знак коэффициента говорит о направлении связи
Задача множественного регрессионного анализа.
Регрессионный анализ – это статистический метод исследования зависимости случайной величины Y от переменных Xj (j = 1, 2, k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения Xj.
Регрессионный анализ используют для решения следующих задач:
§ установления формы зависимости между переменными (линейная-нелинейная, отрицательная-положительная);
§ определения функции регрессии. Важно выяснить, каково было бы действие на зависимую переменную главных факторов, если бы прочие факторы не изменялись и если бы были исключены случайные элементы;
§ прогностической оценки неизвестных значений зависимой переменной. С помощью функции регрессии можно воспроизвести значения зависимой переменной внутри интервала заданных значений независимых переменных (интерполяция) или оценить течение процесса вне заданного интервала (экстраполяция).
Одной из задач регрессионного анализа является исследование зависимости одной переменной Y от нескольких объясняющих или независимых переменных X1, X2, Xn в условиях конкретного места и конкретного времени. Эта задача решается с помощью множественного регрессионного анализа.
Наиболеечасто используемая множественная линейная модель регрессионного анализа имеет вид: y = β0+βхi1+βj xij+βk xk+εI, где εi – случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию σ2.
Коэффициент регрессии βj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения.
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии β0, β1, βk.
Так как в регрессионном анализе xj рассматриваются как неслучайные величины, а Mεi = 0, то уравнение регрессии имеет вид: y= β0+β1хi1+ βj xij+βk xk, где i=1, 2, n; у=xβ (матричная форма).
При построении модели множественной линейной регрессии учитываются следующие пять условий:
2. математическое ожидание случайной ошибки уравнения регрессии
равно нулю во всех наблюдениях: М (ε) = 0, i= 1,m;
3. дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдений: D(ε) = σ2 = const;
4. случайные ошибки модели регрессии не коррелируют между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): соv(εi,εj.) = 0, i≠j;
Машинное обучение — 1. Корреляция и регрессия. Пример: конверсия посетителей сайта
Как и обещал, начинаю цикл статей по «машинному обучению». Эта будет посвящена таким понятиям из статистики, как корреляция случайных величин и линейная регрессия. Рассмотрим, как реальные данные, так и модельные (симуляцию Монте-Карло).
Часть 1. Реальные данные
Чтобы было интереснее, рассказ построен на примерах, причем в качестве данных (и в этой, и в следующих, статьях) я буду стараться брать статистику прямо отсюда, с Хабра. А именно, неделю назад я написал свою первую статью на Хабре (про Mathcad Express, в котором и будем все считать). И вот теперь статистику по ее просмотрам за 10 дней и предлагаю в качестве исходных данных. На графике это ряд Views, синяя линия. Второй ряд данных (Regs, с коэффициентом 100) показывает число читателей, выполнивших после прочтения определенное действие (регистрацию и скачивание дистрибутива Mathcad Prime).
Так уж получилось, что у меня, кроме статистики просмотра статьи (с Хабра), был доступ к статистике скачиваний Mathcad (по ссылке, которую я дал внутри текста статьи). Таким образом, у нас все есть для того, чтобы разобраться с таким понятием интернет-маркетинга, как конверсия. Конверсией обычно называют отношение числа посетителей сайта, выполнивших на нём покупку, регистрацию или т.п. к общему числу посетителей. Например: в первый день публикации мою статья была просмотрена 5 тыс. раз, а скачиваний было 20, т.е. конверсия составила 0.4%.
Все картинки — это скриншоты Mathcad Express (сами расчеты можете взять здесь, повторить, а при желании изменить и использовать для своих нужд). Исходные данные (три вектора) я ввел руками:
Вот расчеты конверсии (в %): «мгновенной» (для каждого дня) и «средней» (за 10 дней). Любопытно, что значение конверсии немного «плывет» со временем (от 0.4% в первый день до квази-стационарного 1% в последние дни), что, само по себе, достойно обсуждения (которое отложим до следующих статей — про случайные процессы и время корреляции).
Тот очевидный факт, что число целевых действий (скачиваний) зависит от числа просмотров, наглядно продемонстрирует график Regs(Views). Мы видим, что, хотя и число просмотров, и число скачиваний — случайные, тем не менее они связаны между собой (почти) линейной зависимостью.
Теперь немного «школьной» статистики: вычисление (по определению) среднего значения, дисперсии и коэффициента корреляции двух выборок Views и Regs.
Последняя формула — это вычисление коэффициента корреляции — меры того, насколько зависимыми являются две случайные величины (точнее, меры линейной зависимости). Получается, что выборочное значение коэффициента корреляции равно 0.97. Это очень много (что, впрочем, и неудивительно, по самой постановке задачи).
Наконец, решим задачу математической регрессии — приближения, в общем случае, выборки данных (x,z) определенной функцией f(x), определенным образом минимизирующей совокупность ошибок f(x)-z. Самый простой и наиболее часто используемый вид регрессии — линейная, когда f(x)=A*x+B. Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты A и B вычисляются обычно из условия минимизации суммы квадратов ошибок:
К слову, метод наименьших квадратов (минимизация суммы квадратов ошибок) — не единственно возможный вариант построения регрессии. Например, иногда применяется медиан-медианная линейная регрессия.
Наконец, о том, для чего нужна регрессия в нашей задаче. Если принять линейный характер зависимости скачиваний от просмотров, то коэффициент А как раз и будет характеризовать конверсию. Судя по нему, конверсия равна 0.005=0.5%, т.е., если, к примеру, у нас есть маркетинговая цель — достичь показателя 100 скачиваний, то, исходя из модели линейной регрессии, нам надо «залить» на сайт 100/0.005=20 тыс. просмотров.
Часть 2. Моделирование Монте-Карло
В то время как в прошлой части мы оперировали случайными данными, полученными в ходе эксперимента, в заключение повторим те же расчеты при помощи датчика псевдослучайных чисел. В методах Монте-Карло часто требуется создавать случайные числа с определенной корреляцией. Для начала сгенерируем три псевдослучайных массива: х и y — независимые, а z — зависящий от х (с «генеральным» значением коэффициента корреляции r):
На графике слева показана зависимость некоррелированых случайных значений х и y, а справа — зависимость коррелированых z и х.
Используя те же формулы, что в прошлом разделе, получим статистические характеристики выборок х, y и z (в том числе, выборочное значение коэффициента корреляции):
Ну, и, наконец, по формуле метода наименьших квадратов построим линейную регрессию z=A*x+B:
Заинтересовавшимся читателям оставляю поэкспериментировать с параметром r и посмотреть, как его изменение будет влиять на зависимость z(x). Еще любопытно, изменяя объем выборки N, следить за результатом расчета статистических характеристик.
Корреляция и регрессия
Когда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой?
В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными.
Цели
По завершении этого модуля вы сможете:
Раздел 1. Корреляция
В этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции.
Что такое корреляция?
Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная.
Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий.
Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее.
Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий.
Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных.
Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается.
Диаграмма, указывающая на корреляцию между двумя количественными переменными
Корреляция против причинно-следственной связи
Теперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию.
Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи.
Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему.
Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде.
Измерение корреляции
Корреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1.
Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается.
На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0.
Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности.
Идеальная положительная корреляция
Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений.
Идеальная отрицательная корреляция
Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений.
Нет линейной корреляции
Когда r = 0, линейная зависимость между переменными не наблюдается.
С реальными данными вы никогда не увидите значений r «–1», «0» или «1».
Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице.
Сила корреляции
Очень сильная корреляция
Очень слабая корреляция или ее нет вообще
Условие корреляции
Чтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов.
В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов.
Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции.
Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех.
Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов.
Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения.
Проверка знаний
Силу корреляции при значении r, равному –0,52, лучше всего можно описать как:
Резюме
Итак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии.
Раздел 2. Линейная регрессия
На предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными.
Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y.
Диаграмма рассеяния с линией регрессии
Линия регрессии
Как и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:
Как и корреляция, линейная регрессия отображается на диаграмме рассеяния
Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»).
Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X.
Чтобы было понятнее, давайте рассмотрим пример.
Пример регрессии
Представьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов.
Давайте используем для этого линейную регрессию.
Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x).
Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов?
Диаграмма рассеяния цен на дома и квадратных метров
Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии.
Уравнение линии регрессии
Уравнение линии регрессии: Y = 113x + 98,653 (с округлением).
Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение:
Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».
Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0».
Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов.
Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов?
Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов.
Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов?
Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений.
Величина достоверности аппроксимации
Наведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r.
В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации).
Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии).
Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%.
Корреляция против причинно-следственной связи
Теперь давайте рассмотрим, как отличить линейную регрессию от корреляции.
Линейная регрессия
Корреляция
Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии.
Варианты для категорий: «корреляция» или «регрессия».
Измеряется величиной достоверности аппроксимации
Прогнозирует значения Y на основе значений X.
Не предсказывает значения Y из значений X, только показывает взаимосвязь.
Переменные оси X и Y взаимозаменяемы.
Если поменять местами X и Y, результаты анализа изменятся.
Резюме
Итак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них.
15 Корреляция и регрессия
15.1 Дисперсия и стандартное отклонение
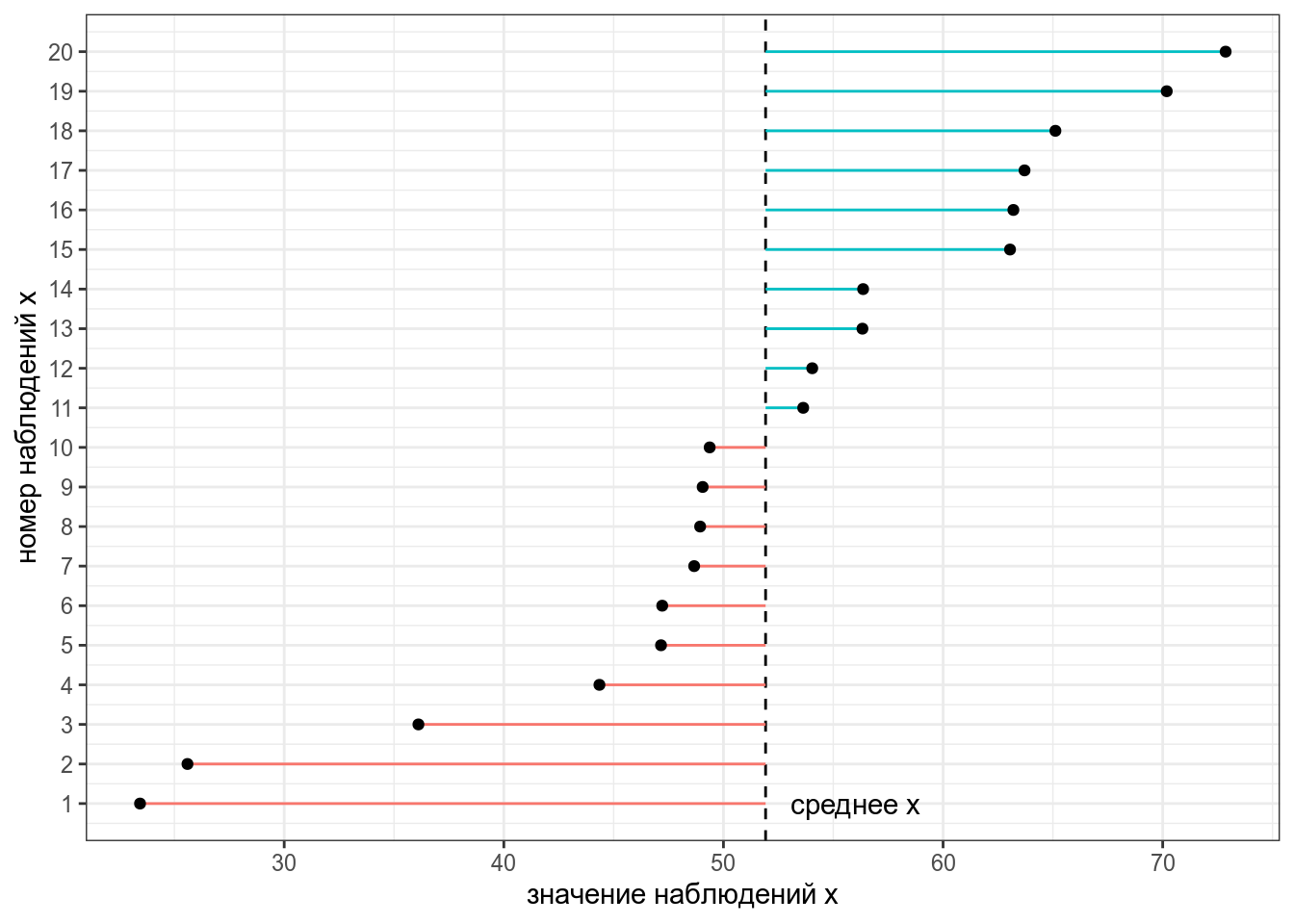
Дисперсия — мера разброса значений наблюдений относительно среднего.
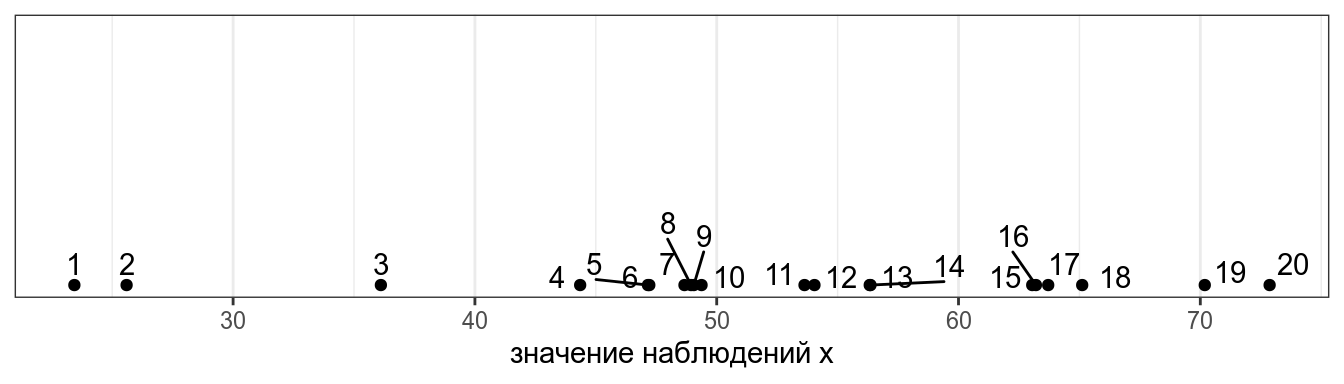
Представим, что у нас есть следующие данные:
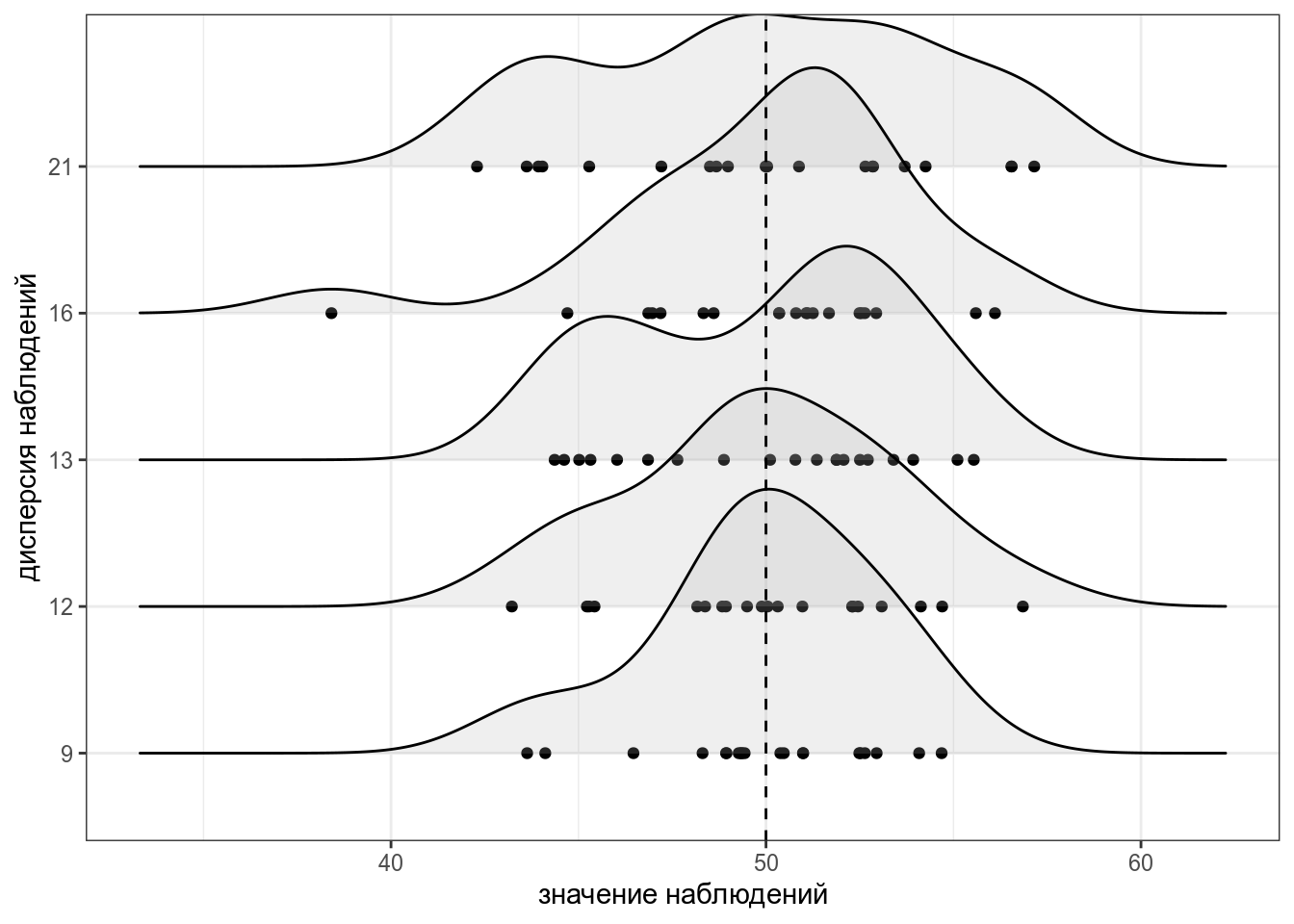
Для того чтобы было понятнее, что такое дисперсия, давайте рассмотрим несколько расспределений с одним и тем же средним, но разными дисперсиями:
Проверим, что функция выдает то же, что мы записали в формуле.
Так как дисперсия является квадратом отклонения, то часто вместо нее используют более интерпретируемое стандартное отклонение \(\sigma\) — корень из дисперсии. В R ее можно посчитать при помощи функции sd() :
15.2 z-преобразование
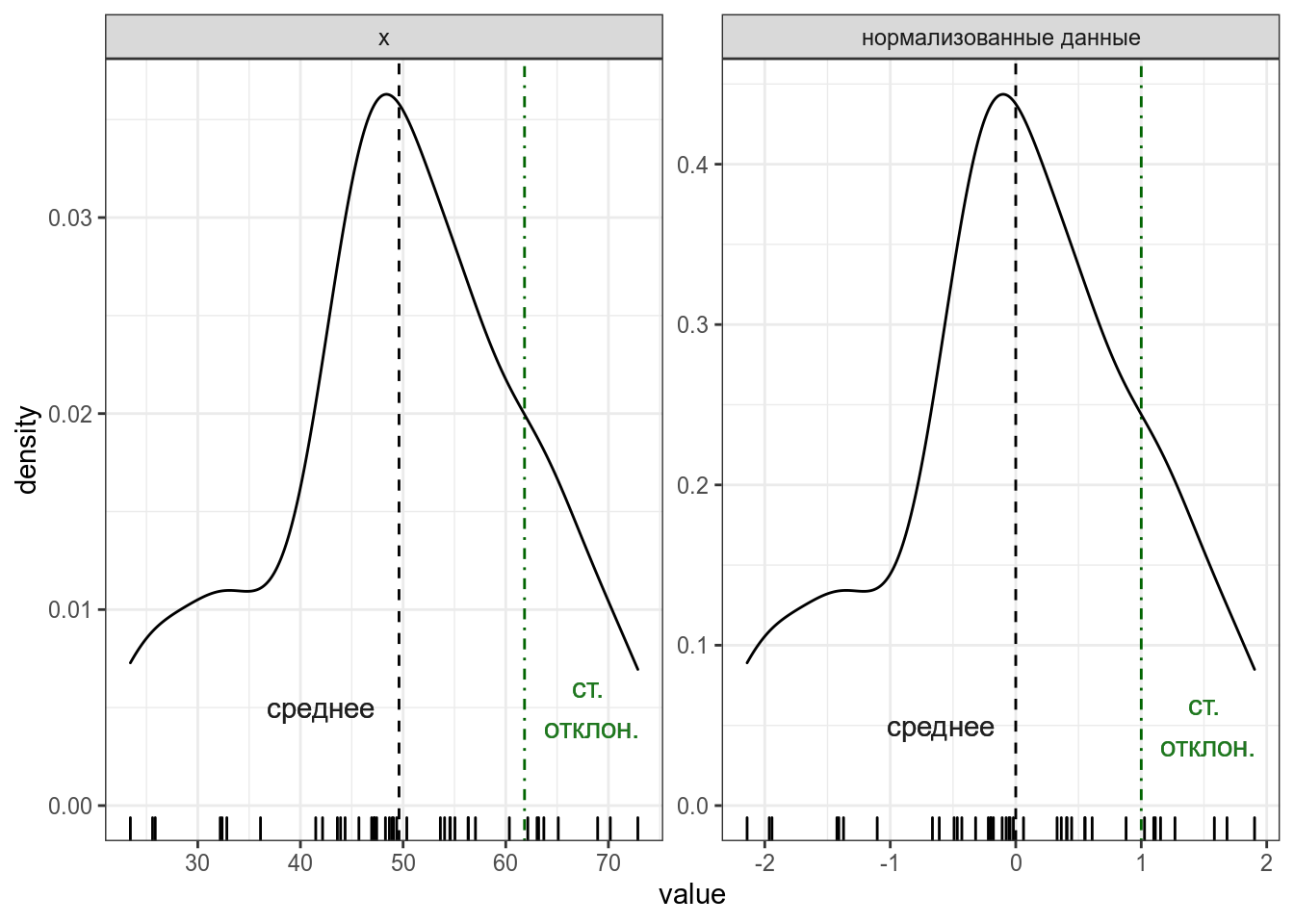
z-преобразование (еще используют термин нормализация) — это способ представления данных в виде расстояний от среднего, измеряемых в стандартных отклонениях. Для того чтобы его получить, нужно из каждого наблюдения вычесть среднее и результат разделить на стандартное отклонение.
Если все наблюдения z-преобразовать, то получиться распределение с средним в 0 и стандартным отклонением 1 (или очень близко к ним).
Проверим, что функция выдает то же, что мы записали в формуле.
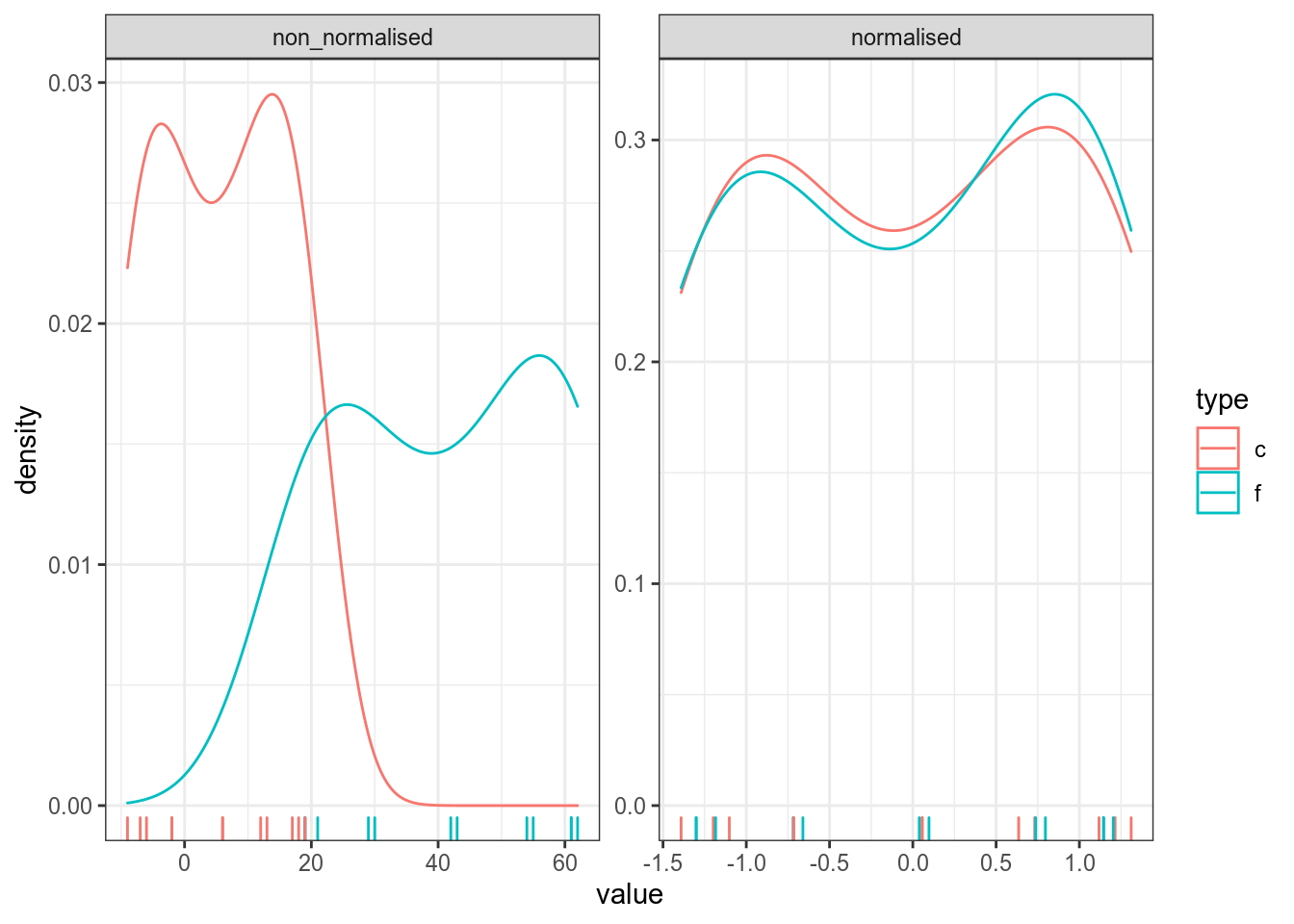
Однаждый я заполучил градусник со шкалой Фаренгейта и целый год измерял температуру в Москве при помощи градусников с шкалой Фарингейта и Цельсия. В датасет записаны средние значения для каждого месяца. Постройте график нормализованных и ненормализованных измерений. Что можно сказать про измерения, сделанные разными термометрами?
15.3 Ковариация
Ковариация — эта мера ассоциации двух переменных.
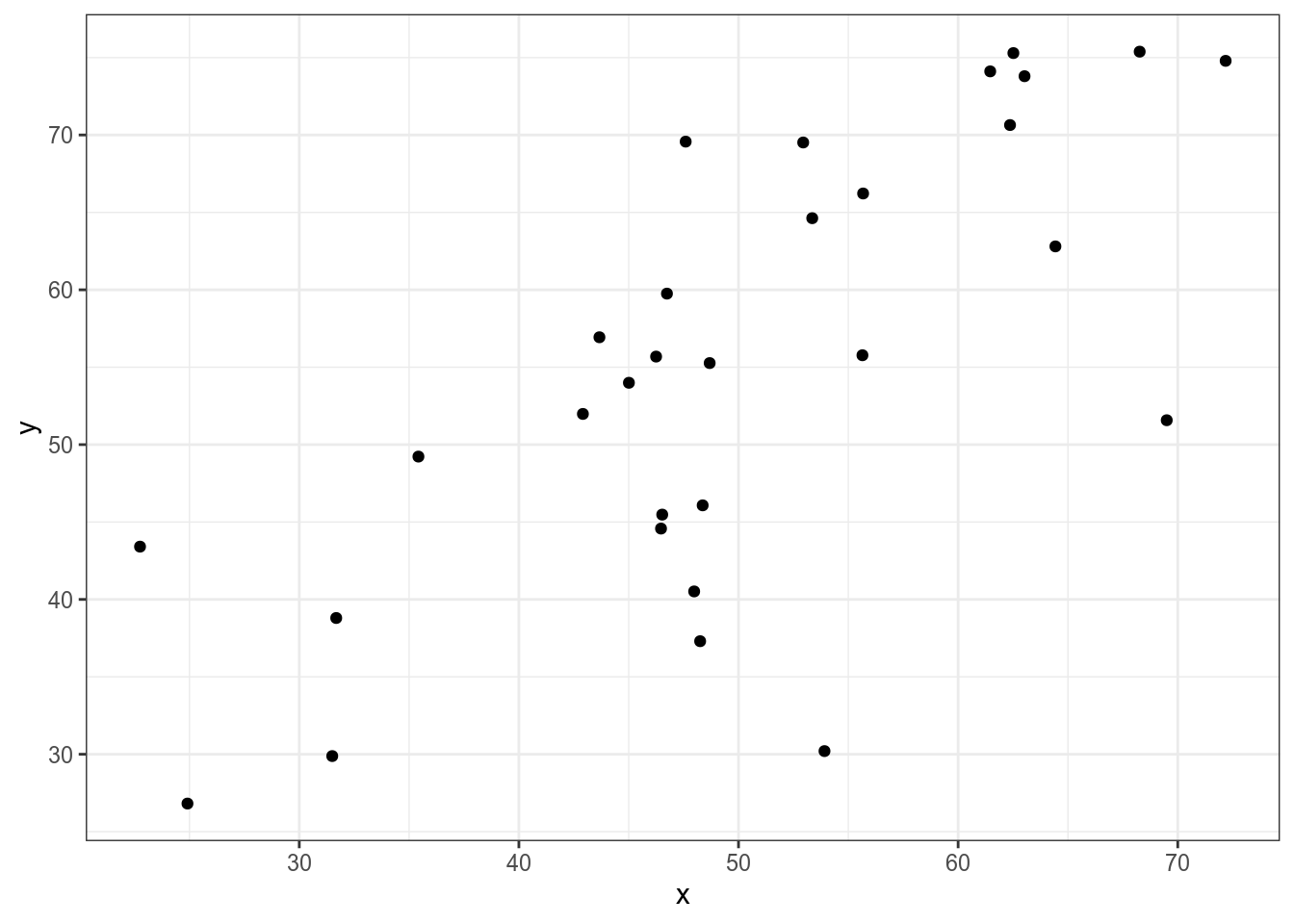
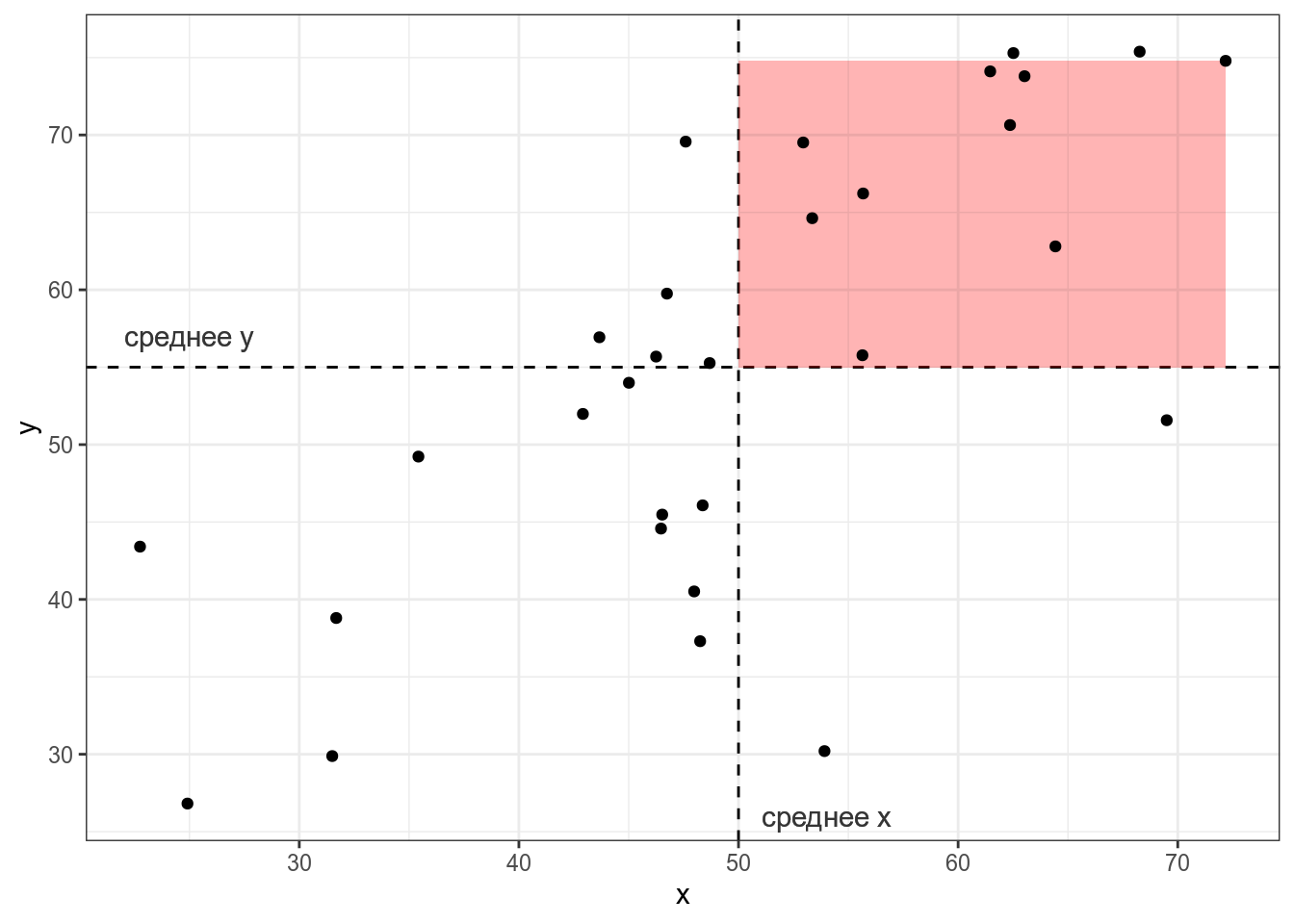
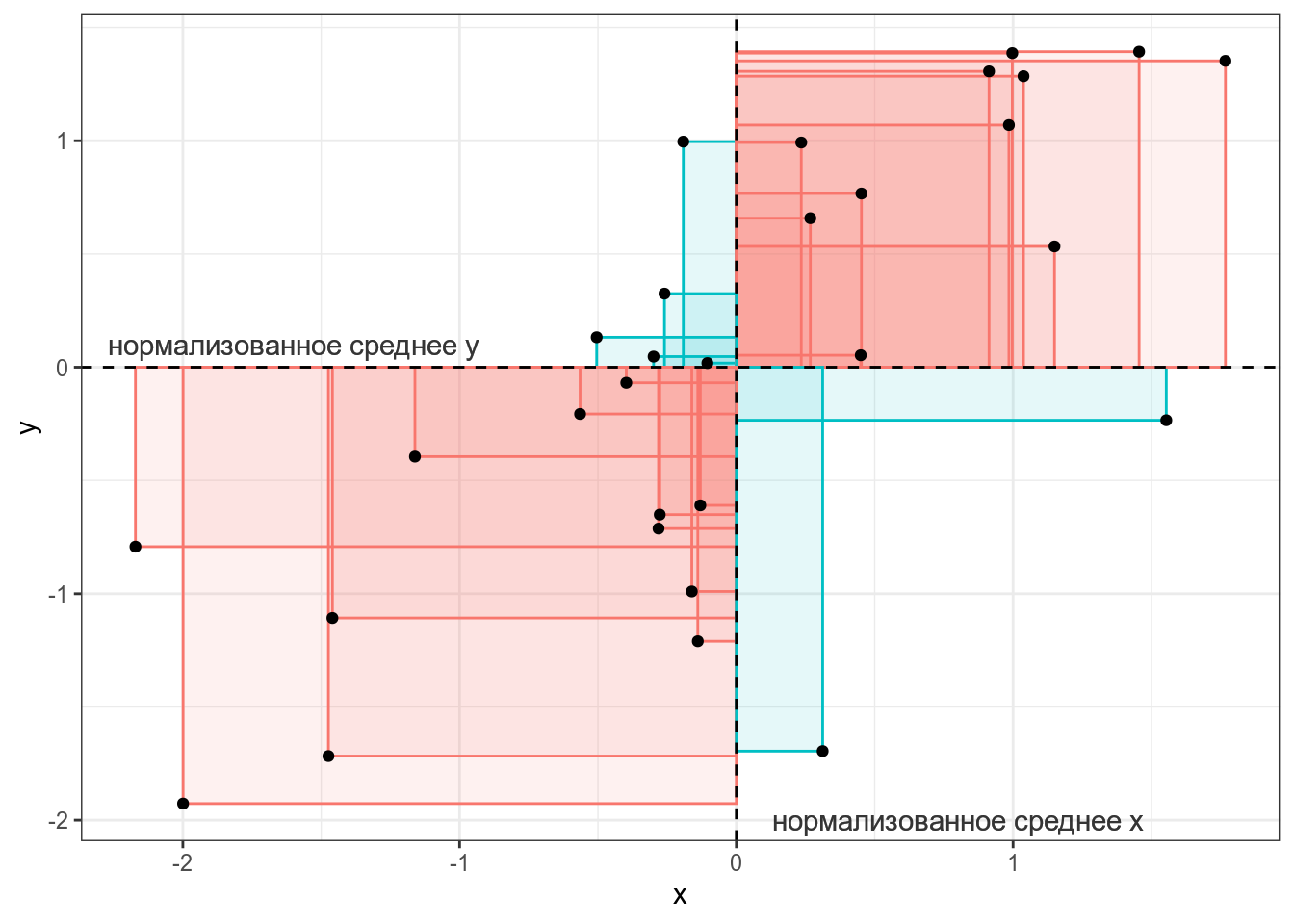
Представим, что у нас есть следующие данные:
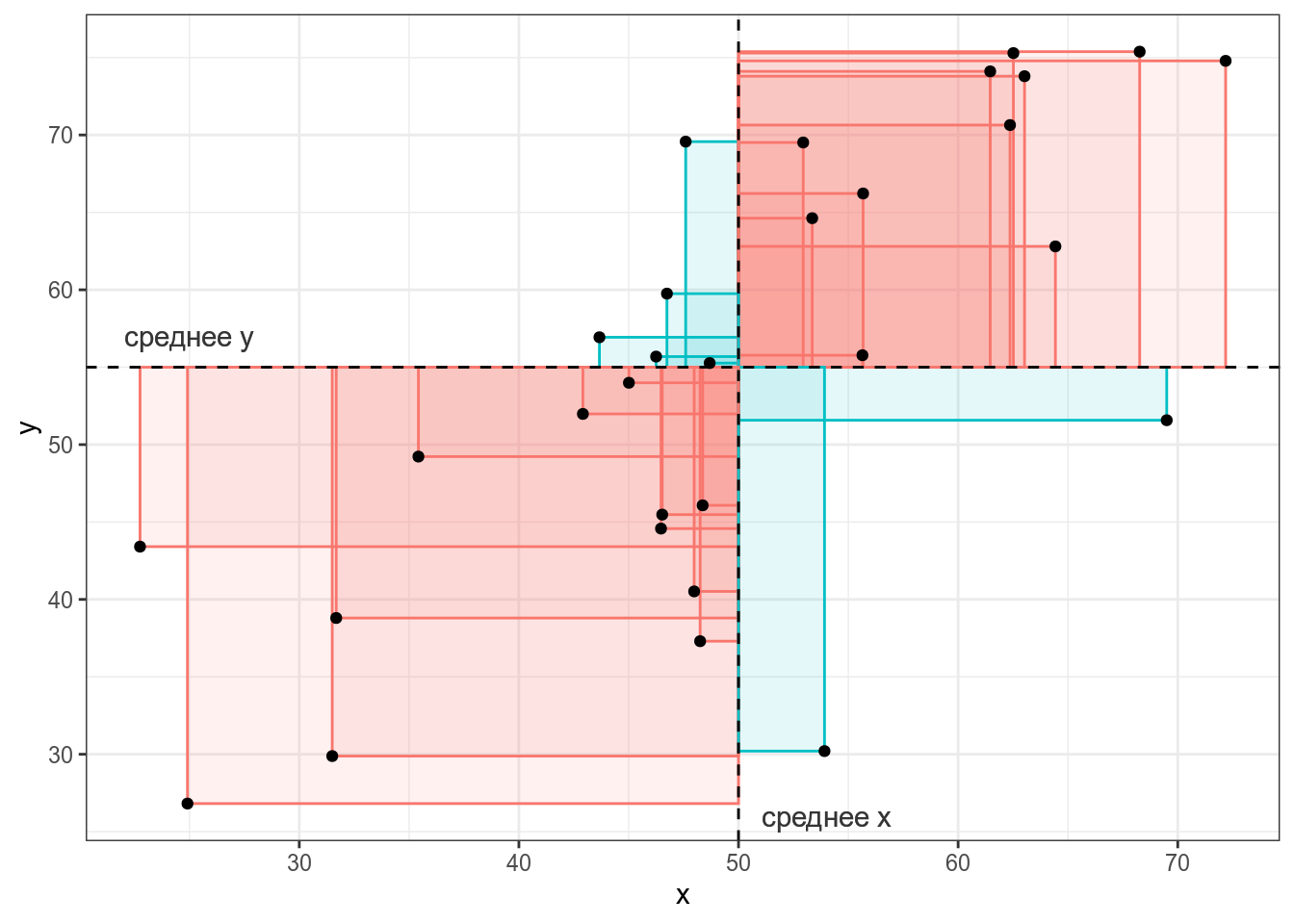
Тогда, согласно формуле, для каждой точки вычисляется следующая площадь (пуктирными линиями обозначены средние):
Как видно, простое умножение на два удвоило значение ковариации, что показывает, что непосредственно ковариацию использовать для сравнения разных датасетов не стоит.
Проверим, что функция выдает то же, что мы записали в формуле.
15.4 Корреляция
Корреляция — это мера ассоциации/связи двух числовых переменных. Помните, что бытовое применение этого термина к категориальным переменным (например, корреляция цвета глаз и успеваемость на занятиях по R) не имеет смысла с точки зрения статистики.
15.4.1 Корреляция Пирсона
Коэффициент корреляции Пирсона — базовый коэффициент ассоциации переменных, однако стоит помнить, что он дает неправильную оценку, если связь между переменными нелинейна.
Эта нормализация приводит к тому, что
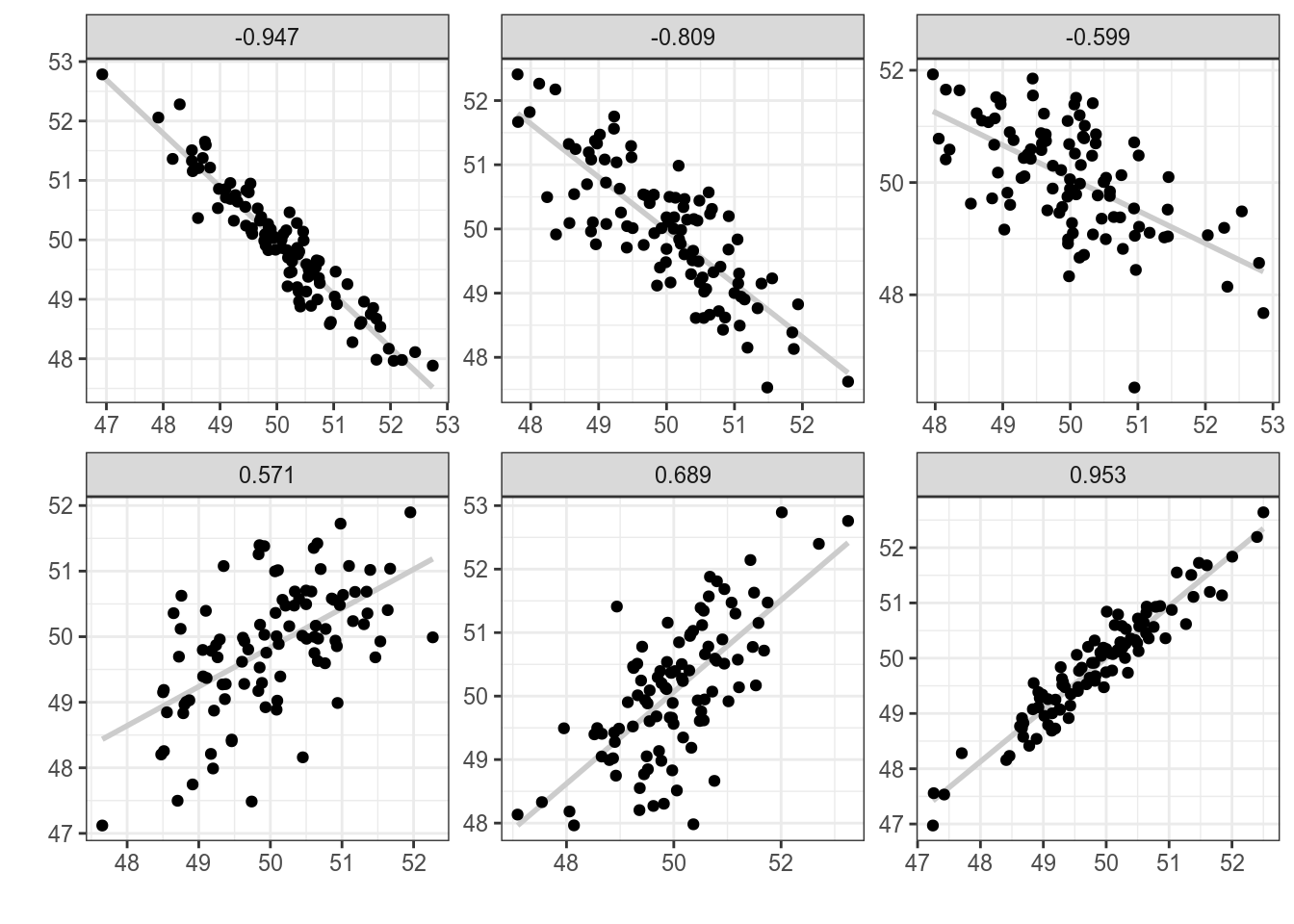
Для того чтобы было понятнее, что такое корреляция, давайте рассмотрим несколько расспределений с разными значениями корреляции:
Как видно из этого графика, чем ближе модуль корреляции к 1, тем боллее компактно расположены точки друг к другу, чем ближе к 0, тем более рассеяны значения. Достаточно легко научиться приблизительно оценивать коэфициент корреляции на глаз, поиграв 2–5 минут в игру “Угадай корреляцию” здесь или здесь.
Проверим, что функция выдает то же, что мы записали в формуле.
Посчитайте на основе датасета с температурой корреляцию между разными измерениями в шкалах Фарингейта и Цельсия? Результаты округлите до трех знаков после запятой.
15.4.2 Ранговые корреляции Спирмана и Кендалла
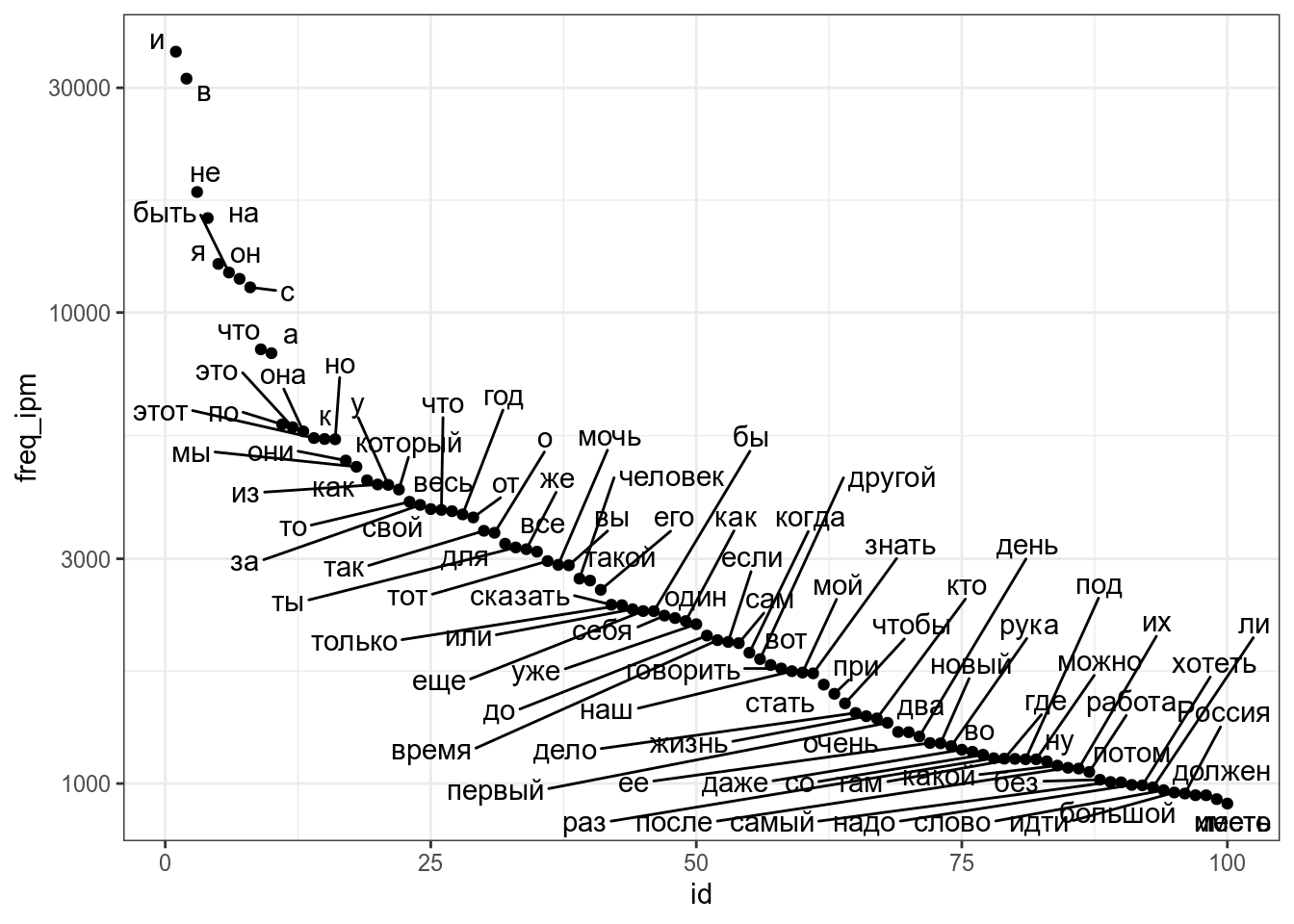
Коэффициент корреляции Пирсона к сожалению, чувствителен к значениям наблюдений. Если связь между переменными нелинейна, то оценка будет получаться смещенной. Рассмотрим, например, словарь [Ляшевской, Шарова 2011]:
В целом корреляция между рангом и частотой должна быть высокая, однако связь между этими переменными нелинейна, так что коэффициент корреляции Пирсона не такой уж и высокий:
Для решения той проблемы обычно используют ранговые коэффециенты коррляции Спирмана и Кендала, которые принимают во внимание ранг значения, а не его непосредственное значение.
Давайте сравним с предыдущими наблюдениями и их логаотфмамиы: