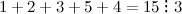Краткие числа что это
Кратное и делитель
Если одно натуральное число делится без остатка на другое натуральное число, то первое называется кратным второго, а второе — делителем первого.
Кратное числа — это делимое, которое делится на данный делитель без остатка.
Делитель числа — это делитель, на который делимое делится без остатка.
Пример. Возьмём, например, такое деление:
Число 6 делится на число 3 без остатка. Следовательно, число 6 — кратное числа 3, а число 3 — делитель числа 6.
Пусть m и n — натуральные числа, если число m является кратным числа n, то говорят: m кратно n или m делится на n
Пример. 6 кратно 3 (шесть кратно трём) или 6 делится на 3 (шесть делится на три).
Самым маленьким кратным любого натурального числа является само это число, так как любое натуральное число можно разделить само на себя без остатка (в частном всегда будет единица).
Пример. Для числа 7 наименьшим кратным является число 7, для числа 2 — число 2:
7 : 7 = 1 (семь кратно семи);
2 : 2 = 1 (два кратно двум).
Для любого натурального числа существует бесконечно много кратных. Получить кратное для данного числа достаточно легко, можно просто умножить его на любое натуральное число, полученное произведение и будет его кратным.
Пример. Получим кратное числа 5, умножив его, например, на 2:
Число 10 — кратное числа 5:
Так как на единицу делится любое натуральное число, то число 1 является делителем любого натурального числа.
Кратное число

Всего получено оценок: 161.
Всего получено оценок: 161.
Математика имеет много специфических понятий, среди которых кратное число и делимость чисел. Сегодня мы разберем понятие кратности, а так же все понятия из математики 6 класса, которые связаны с кратностью.
Деление
Операция деления является обратной для операции умножения. Деление показывает, сколько раз одно число умножили на другое, чтобы получить изначальный результат. Для нахождения результата простейших операций деления пользуются таблицей умножения.
Для более сложных примеров пользуются деление в столбик. Так же различают деление с остатком, нацело и деление с дробным остатком:
Так же вместо деления всегда можно записать обычную или неправильную дробь, но в качестве ответа такая запись не подойдет.
Отрицательные числа так же можно поделить нацело. Так же, как и в делении отрицательных чисел на положительные и положительные на отрицательные. Нельзя так же забывать, что на деление действует правило знаков. То есть деление отрицательного числа на положительное дает отрицательный результат. Деление отрицательного числа на отрицательное – положительный результат.
Кратность и делимость
Разберем эти понятия на числе 9. Так для числа 9 кратными будут 18, 27, 36 и так далее. То есть кратными называют числа, которые можно поделить на заданное число нацело.
Делимостью же называют способность самого числа поделиться нацело. То есть для 9 делителями будут числа 9,3,1. Число делителей – ограниченно, число кратных – нет.
Бывают числа кратные для нескольких значений одновременно.
Для нескольких чисел существует два понятия, связанных с делимостью и кратностью:
Иногда ученики пытаются найти таблицу кратных чисел. Но такого материала просто не существует. Нельзя свести в одну таблицу все числа. А для наиболее простых от 1 до 10 существует таблица умножения.
Что мы узнали?
Мы вспомнили, что такое операция деления. Рассказали, что такое кратность и делимость чисел. Разделили два этих понятия. Сказали о том, что таблицы кратности в математике пока не изобрели. Рассказали, в каких математических показателях используются понятия кратности и делимости.
Что такое кратное число
Определение кратного числа
Некоторые признаки делимости натуральных чисел
Признак делимости на 2.
Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.
Признак делимости на 3.
Число делится на 3, если сумма его цифр делится на 3.
Признак делимости на 4.
Признак делимости на 5.
Число делится на 5, если оно заканчивается либо на 0, либо на 5.
Признак делимости на 8.
Признак делимости на 9.
Число делится на 9, если сумма его цифр делится на 9.
Признак делимости на 11.
Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.
Признак делимости на 25.
Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:
$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$
Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:
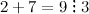


Таким образом, на 3 делятся числа:
$$27 ; 36 ; 1119: 12354$$
Наименьшее общее кратное (НОК)
Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).
Алгоритм нахождения наименьшего общего кратного нескольких чисел:
Что такое кратное число не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти НОК(360; 420)
Решение. Запишем каноническое разложение заданных чисел:
Какие числа кратны 10
Содержание статьи
Термин «кратность» относится к области математики: с точки зрения этой науки, он означает количество раз, которое определенное число входит в состав другого числа.
Понятие кратности
Второе важное свойство касается определения наименьшего целого числа, являющегося кратным рассматриваемому. Так, наименьшим кратным по отношению к любому числу является само это число. Это связано с тем, что наименьшим целым результатом деления одного числа на другое является единица, а именно деление числа само на себя и обеспечивает этот результат. Соответственно, число, кратное рассматриваемому, не может быть меньше, чем само это число. Например, для числа 3 наименьшим кратным числом будет 3. При этом определить наибольшее число, кратное рассматриваемому, фактически невозможно.
Числа, кратные 10
Числа, кратные 10, обладают всеми перечисленными свойствами наравне с другими кратными числами. Так, из перечисленных свойств следует, что наименьшим числом, кратным 10, является само число 10. При этом, поскольку число 10 является двузначным, можно сделать вывод, что кратным числу 10 могут быть только числа, состоящие не менее чем из двух знаков.
Для того чтобы получить другие числа, кратные 10, необходимо число 10 умножить на любое целое положительное число. Таким образом, в перечень чисел, кратных 10, войдут числа 20, 30, 40, 50 и так далее. Следует обратить внимание, что все полученные числа должны без остатка делиться на 10. При этом определить наибольшее число, кратное 10, как и в случаях с другими числами, невозможно.
Кроме того, обратите внимание, что существует простой практический способ определить, является ли конкретное рассматриваемое число кратным 10. Для этого следует выяснить, какова его последняя цифра. Так, если она равна 0, рассматриваемое число будет кратным 10, то есть может быть без остатка разделено на 10. В противном случае число не является кратным 10.
Разряды и классы чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.