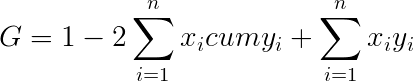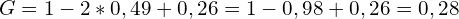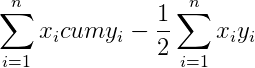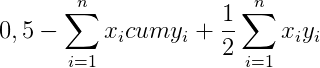Кривая лоренца используется для характеристики чего
Кривая Лоренца
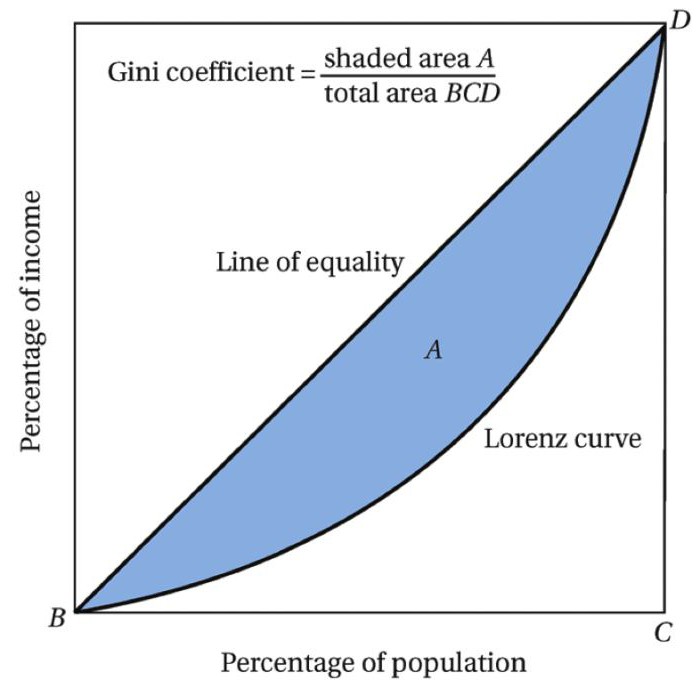
Кривая Лоренца (Lorenz curve) — график, демонстрирующий степень неравенства в распределении дохода в обществе, отрасли, а также степени неравенства в распределении богатства. Если обратиться к кривой Лоренца показывающей степень неравенства в распределении дохода в обществе, то график или кривая Лоренца будет отражать долю дохода, приходящуюся на различные группы населения сформированные на основании размера дохода, который они получают.
Неравенство доходов в конце XIX — начале XX века стало объектом изучения многих экономистов США и Западной Европы. Центральной проблемой изучения является оценка справедливости и эффективности сложившегося в рыночной экономике распределения доходов и богатства. В 1905 году американский статистик Макс Лоренц разработал метод оценки распределения доходов, получивший название кривой Лоренца.
На оси абсцисс откладывается доля населения, а на оси ординат — доля доходов в обществе в процентном отношении. Как видно из графика, в обществе всегда имеет место быть неравенство в распределении доходов, что отражает кривая \mathrm
Если бы в обществе было бы равное распредение дохода, то кривая Лоренца приняла бы вид прямой (биссектриса на графике), называемая линией абсолютного равенства, и, наконец, если бы в обществе весь доход получали только 1% населения, то на графике это выразилось бы вертикальной прямой линией, называемой линией абсолютного неравенства.
На основании кривой Лоренца можно вывести коэффициент Джинни.
Кривая Лоренца. Неравенство распределения доходов
Неравенство распределения доходов заложено в самой сущности рыночной экономики. Даже в идеально справедливом обществе оно будет существовать, поскольку все мы отличаемся природными способностями. Неравенство распределения доходов обычно иллюстрирует ситуация, когда маленькая часть населения обладает существенной долей национального богатства, и наоборот. Для его измерения используется, в частности, кривая Лоренца.
Распределение богатства
В любой стране есть богатые и бедные граждане. Первые обладают львиной долей национального богатства, вторые – едва сводят концы с концами. В краткосрочном периоде мы наблюдаем неравенство распределения доходов. В перспективе – несправедливость накопления богатства элитами.
История формирования концепции
Кривая Лоренца
Предположим, мы хотим изобразить несправедливость распределения богатства в государстве. Для этого нам понадобятся доходы населения. Кривая Лоренца строится в четыре этапа:
Кривая Лоренца позволяет визуализировать неравенство распределения доходов. Можно совместить несколько графиков для того, чтобы показать изменения на протяжении времени или сравнить ситуацию в ряде стран.
Как построить кривую Лоренца на практике
Предположим, что в рассматриваемой нами отрасли есть десять фирм, которые различаются по своему вкладу в экономику. Если бы у нас были доходы населения, кривая Лоренца бы показывала неравенство их распределения. В этом случае она иллюстрирует справедливость разделения рынка. Для того чтобы построить кривую Лоренца, в этом случае необходимо:
Коэффициент Джини
Мы рассмотрели особенности построения графика распределения доходов. За визуальную сторону вопроса отвечает кривая Лоренца. Коэффициент Джини оперирует числовыми значениями. Он измеряется соотношением точек на реальном графике с идеальным случаем (прямой линией, которая образует с осью абсцисс угол в 45 градусов). Коэффициент Джини может принимать значения от 0 до 1. В первом случае мы имеем дело с абсолютной справедливостью распределения доходов, во втором – с полным неравенством, когда один человек обладает всем национальным богатством, а другим не остается ничего. Естественно, оба случая нереальны. Однако важно понимать, что меньшее значение коэффициента указывает на лучшую ситуацию в экономике государства.
Проблемы использования коэффициента
Индекс Джини полностью базируется на показателях валового национального продукта и статистике доходов населения. Многие развивающиеся страны не предоставляют точных сведений, что не дает правильно оценить ситуацию с распределением богатства в них. Также существует обратно пропорциональная зависимость между коэффициентом Джини и валовым внутренним продуктом на душу населения. Это связано с тем, что в более бедных странах проблемы существеннее.
Интерпретация показателей
Когда мы разобрались, как построить кривую Лоренца, важно понять, что же все-таки она значит. Как можно сопоставлять страны с различными уровнями ВВП? Кривая Лоренца и коэффициент Джини используются для того, чтобы понять, насколько справедливо распределяется национальное богатство государства. Нужно понимать, что государства с самыми низкими показателями – это необязательно самые богатые страны. Сходные валовые продукты не указывают на одинаковую форму кривой на графике распределения доходов.
Глубина бедности
Неравенство распределения доходов приводит к тому, что 10% населения отрываются на полную, а нижний дециль вынужден выживать на 1,25 доллара США в день. Все, кто зарабатывают меньше этой суммы, вообще считаются живущими за гранью бедности. Однако нужно понимать, что в каждой стране своя цена жизни, поэтому этот стандарт необходимо корректировать с поправкой на национальные особенности.
Группа по исследованию развития Всемирного банка рассчитывает специальный показатель глубины бедности. Для этого используются показатели доходов и потребления домохозяйств 115 стран. Отчеты по показателю выходят два раза в год: в апреле и сентябре.
Социальная политика государства
Высокая степень неравномерности распределения доходов является причиной забастовок и даже революций. Поэтому цель любого правительства состоит в том, чтобы сделать это явление менее заметным и смягчить разрыв между богатыми и бедными. Социальная политика государства обычно связана с развитием справедливых отношений в обществе, формированием защитных механизмов и созданием условий для роста благосостояния населения. Для этого правительству приходится решать следующие задачи:
Выводы
Идеального общества абсолютной справедливости не существует. Есть только государства с большим или меньшим коэффициентом Джини. Чем меньше разрыв между идеальной и реальной кривой Лоренца, тем лучше распределяются доходы в стране. Проблема несправедливости накопления богатства отдельными лицами или группами характерна для многих современных государств, особенно развивающихся. Для частичного решения этой проблемы необходима грамотная национальная социальная политика. Ее результативность оценивают, сравнивая уровень и качество жизни в различных странах или за определенный период. Важно не допустить достижения так называемого социального дна и прогрессирования диспропорциональности. Если государство справляется со своими функциями, то население, даже бедное, должно чувствовать улучшение уровня жизни. И это связано не столько с изменением формы кривой Лоренца, сколько с расширением потребительской корзины. В противном случае в обществе начинает назревать переворот со всеми его негативными последствиями.
Как рассчитывать коэффициент Джини
Автор: Игорь Святославович Демин · Опубликовано 21.11.2017 · Обновлено 19.01.2021
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
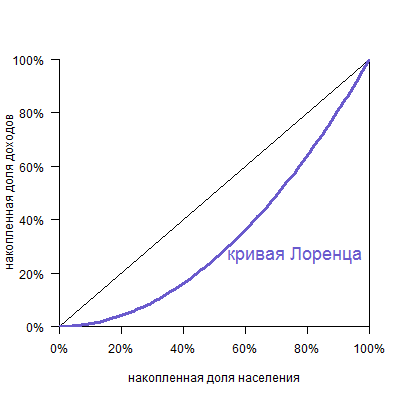
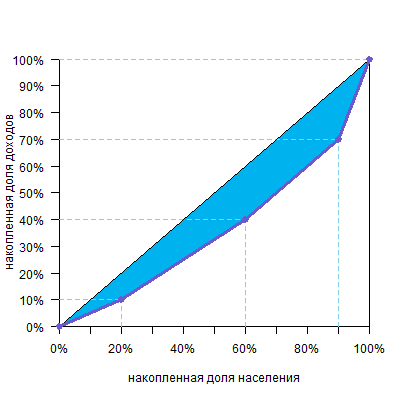
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
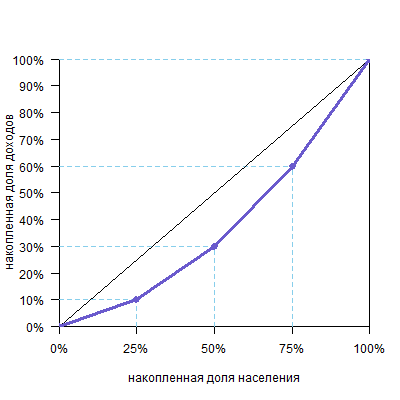
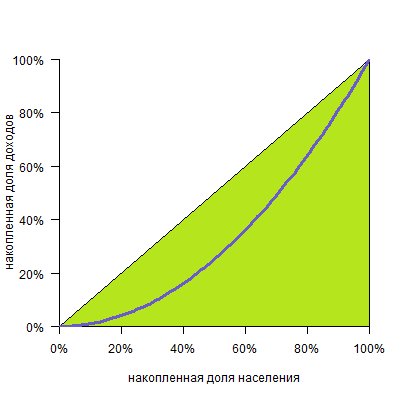
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
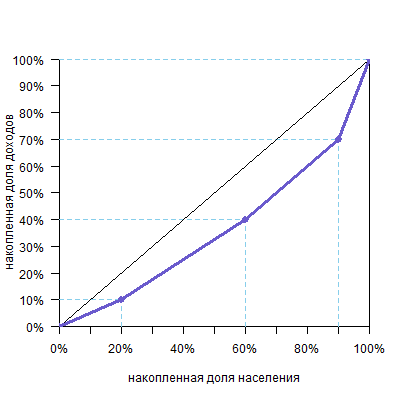
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
Получим такой график:
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
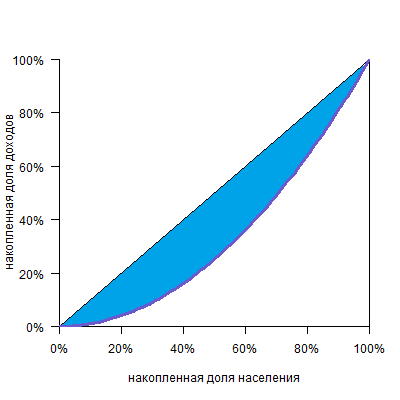
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
К площади треугольника под диагональю (а она всегда равна 0,5):
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
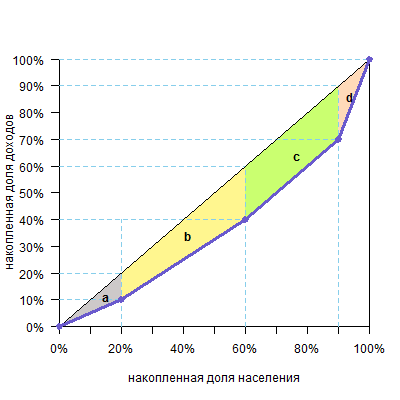
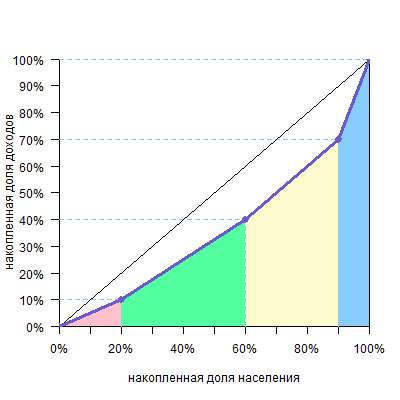
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
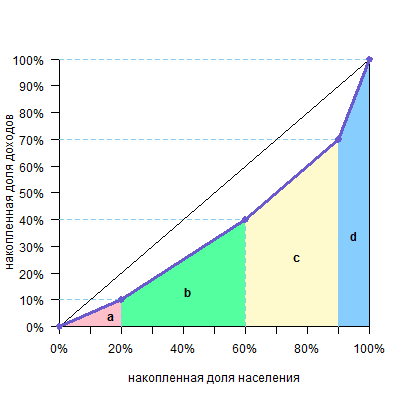
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:
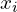
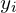
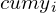
Составим таблицу на основе данных предыдущего примера:
| Доля населения ( 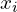 ) ) | Доля от общего дохода ( 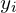 ) ) | Накопленная доля общего дохода ( 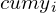 ) ) | 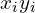 | 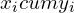 |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Как построена эта таблица
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
Как выведена эта формула?
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
можно сперва посчитать площадь фигуры под кривой Лоренца
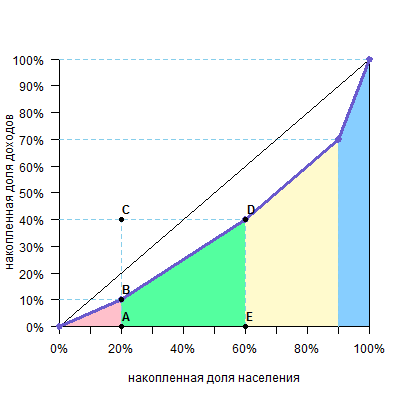
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
Рассмотрим, например, вторую группу (зеленый четырехугольник).
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.\
Кривая Лоренца и коэффициент Джини



Теперь, вспомнив категории личного и располагаемого дохода, можно обратиться к конкретным проблемам неравенства в распределении доходов: какова пропасть между богатыми и бедными? И можно ли вообще измерить неравенство в распределении доходов?
Одним из наиболее известных способов измерения этого неравенства является построение кривой Лоренца, названной так по имени американского экономиста и статистика Макса Лоренца. Речь идет при этом о персональном, а не функциональном распределении доходов.
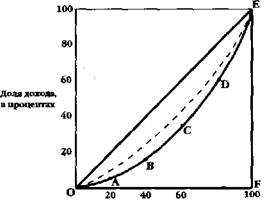
Если мы разделим все население страны на 5 частей (квинтилей), т. е. по 20%, и совокупные доходы общества также по 20%, то можем увидеть, что линия, исходящая из начала осей координат (биссектриса) дает нам представление о равном распределении доходов (см. рис. 24.4).
Кривая Лоренца основана на расчете кумулятивных долей (накопленных долей), и соответственно, построении кумулятивной кривой. На оси абсцисс мы откладываем первые 20% населения; затем, добавив вторую группу, получаем 40% населения, затем 60% и т. д. На оси ординат мы откладываем кумулятивные значения доходов: первые 20%, затем 40%, далее 60% и т. д. Если бы 20% населения получали бы 20% совокупных личных доходов, 40% населения 40% доходов, и т. д., то мы построили бы как раз биссектрису, называемую линией абсолютного равенства.
Доля населения, в % Рис. 24.4. Кривая Лоренца
Очевидно, чем больше отклоняется кривая Лоренца от биссектрисы, тем сильнее неравенство в распределении доходов, и чем активнее социальная политика государства по выравниванию доходов, тем менее вогнута данная кривая. В зависимости от конкретных социальных программ и систем налогообложения в той или иной стране будет зависеть отличие кривых Лоренца, построенной для личных и для располагаемых доходов. Так, в США уменьшение неравенства в распределении располагаемых доходов обусловлено не столько вычетом налогов (американская налоговая система слабопрогрессивна), сколько выплатой трансфертов. Государственные трансфертные платежи в США составляют около 75% дохода группы людей с самыми низкими доходами.
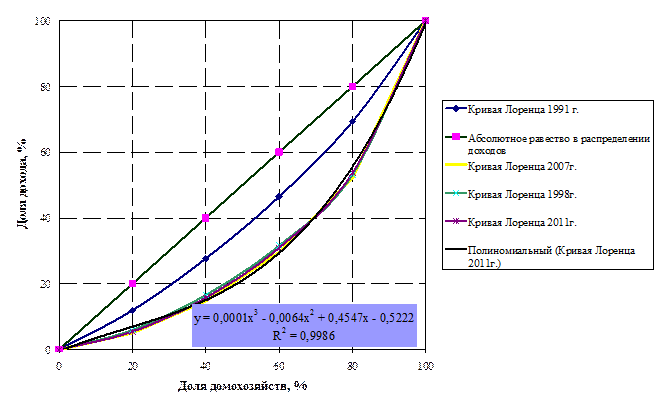
На рис. 24.5 приведены кривые Лоренца для Российской Федерации, отражающие распределение домохозяйств по среднедушевому денежному доходу в Российской Федерации в 1991 г., 1998, 2007, 2011 гг. 1
Рис. 24,5. Кривые Лоренца для России в 1991 г., 1998, 2007, 2011 гг.
Уравнение кривой Лоренца в РФ
x 2 – 42,667х + 1515,667 = 0
Как и отмечалось ранее, больше всего приближается к линии абсолютного равенства кривая Лоренца, отражающая распределение доходов с учетом трансфертных выплат, а далее всего от нее находится кривая, демонстрирующая распределение доходов от собственности.
Так, например, в Швеции, если брать доходы низших 10% и высших 10% групп населения до вычета налогов и получения трансфертов, то соотношение будет 1:100, а если взять соотношение располагаемых доходов, то I : 4.
Еще одним показателем, используемым в экономической науке для определения степени дифференциации доходов, является коэффициент Джини (G). Этот коэффициент тесно связан с кривой Лоренца. На рис. 24.4 мы можем его рассчитать как отношение площади фигуры, находящейся между линией абсолютного равенства и кривой Лоренца (обозначим ее буквой 2), к площади треугольника OFE, образуемого между линиями абсолютного равенства и абсолютного неравенства: *
G = Т/ OFE, где величина G изменяется в пределах от нуля доединицы, т. е. 0
Очевидно, что переход к рыночному механизму распределения ресурсов и доходов неизбежно сопровождается большей дифференциацией доходов населения, нежели в условиях уравнительного распределения в период социалистического хозяйства. При этом необходимо сделать оговорку, что расчеты официальных статистических органов могут не учитывать доходы, не декларируемые субъектами теневой экономики и просто граждан, далеких от законопослушания. Следовательно, в переходной экономике России коэффициент Джини может оказаться величиной еще большей по сравнению с официальными цифрами.
Анализ динамики децильного коэффициента в России демонстрирует те же закономерности: периоды экономических потрясений, высокой инфляции и т. п. сопровождаются усилением разрыва в доходах различных групп населения. Так, в России (сентябрь 1997 г.) на долю 10% наиболее обеспеченной группы населения приходилось 31% денежных доходов, а на долю 10% наименее обеспеченной 2,5%. Таким образом, разрыв в доходах этих групп составил 12,5 раз. В сентябре 1998 г. этот разрыв составил 13,5 раз. Обратим особое внимание на неравномерность децильного коэффициента по различным регионам и отдельным крупнейшим промышленно-финансовым центрам. В 1997 г. он составил в Дальневосточном экономическом районе 16,4; Центрально-Черноземном районе 6,4; в Москве 15,9 раз.
Но почему вообще существует неравенство в доходах? Ведь в демократических странах принято говорить о равенстве возможностей, которые должны обеспечиваться соответствующими институтами рыночной экономики. Различные экономисты называют множество причин и факторов этого неравенства. Отметим лишь самые важнейшие из них.
Во-первых, от рождения люди наделены различными способностями, как умственными, так и физическими. При прочих равных условиях (эту предпосылку нужно всегда иметь в виду), человек, наделенный исключительной физической силой, имеет больше шансов стать знаменитым и высокооплачиваемым спортсменом.
Белая книга. Экономика и политика России в 1997 году. ИЭППП. М., 1998. С.75.
В-третьих, различия в образовательном уровне. Сама эта причина во многом зависит от первых двух названных. Ребенок, родившийся в богатой семье, имеет больше шансов получить превосходное образование и, соответственно, профессию, приносящую высокий доход, нежели дитя в бедной многодетной семье.
В-четвертых, даже при равенстве возможностей и одинаковых стартовых уровнях образования больший доход будут получать лица, которых иногда называют «трудоголиками». Эти люди готовы брать работу на дом, задерживаться по долгу службы на рабочем месте для разрешения той или иной профессиональной проблемы, игнорировать свое неважное самочувствие, лишь бы добиться высоких результатов в своей работе.
В-пятых, есть такая группа причин, которая связана просто с везением, случаем, неожиданным выигрышем и т. п. В условиях неопределенности, характерной для рыночной экономики, эта группа причин может объяснить многие случаи неравенства в распределении доходов.
Таким образом, по крайней мере, в силу названных причин равенство экономических возможностей соблюдается далеко не всегда. Бедные и богатые по-прежнему существуют даже в самых благополучных высокоразвитых странах.
Но что такое бедность? Как определить ее уровень?
Экономисты-теоретики, статистические службы правительства, профсоюзы занимаются исчислением уровня бедности. От этого будут зависеть масштабы и направления перераспределения доходов, построение налоговых систем, систем пенсионного обеспечения и т. п.
Самуэльсон П., Нордхаус В. Экономика. 15 издание. М.,1997. С.
Прожиточный минимум, или черта бедности, говорит нам не о границе выживания, а о некоем минимальном уровне стандарта жизни. Разумеется, этот стандарт будет различным у разных стран и народов, и у одной и той же страны, но на разных исторических этапах ее развития.
По расчетам Самуэльсона и Нордхауса, в 1992 г. доля населения, живущего за чертой бедности в США, составляла 14,5%. По методике Всемирного Банка (прогноз для России), бедным может считать себя тот, у кого на члена семьи приходится меньше 100 руб. (4 долл. США) в день или 3000 руб. в месяц. При таком понимании за чертой бедности в России (на середину 1999 г.) жила половина населения.
Итак, если общество признает справедливым поддержку наименее обеспеченных слоев населения, то конкретной реализацией социальных программ занимается правительство страны.