Кривизна в чем измеряется

Кривизна в чем измеряется

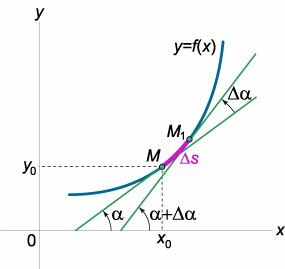
Рассмотрим плоскую кривую, заданную уравнением \(y = f\left( x \right).\) Пусть в точке \(M\left( \right)\) проведена касательная к данной кривой, которая образует угол \(\alpha\) с осью абсцисс (рисунок \(1\)). При смещении \(\Delta s\) вдоль дуги кривой точка \(M\) переходит в точку \(.\) При этом положение касательной также изменяется: угол наклона касательной к оси \(Ox\) в точке \(\) будет составлять \(\alpha + \Delta\alpha.\) Таким образом, при смещении точки кривой на расстояние \(\Delta s\) касательная поворачивается на угол \(\Delta\alpha.\) (Будем считать, что угол \(\alpha\) возрастает при вращении против часовой стрелки.)

Абсолютное значение отношения \(\large\frac<<\Delta \alpha >><<\Delta s>>\normalsize\) называется средней кривизной дуги \(M.\) В пределе, при \(\Delta s \to 0,\) мы получаем кривизну кривой в точке \(M:\) \[K = \lim\limits_ <\Delta s \to 0>\left| <\frac<<\Delta \alpha >><<\Delta s>>> \right|.\] Из приведенного определения следует, что кривизна в какой-либо точке кривой характеризует скорость вращения касательной в этой точке.

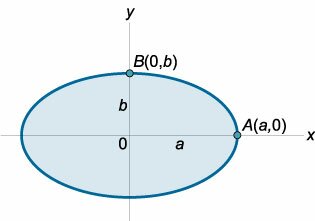
Очевидно, достаточно найти кривизну эллипса в точках \(A\left( \right)\) и \(B\left( <0,b>\right)\) (рисунок \(2\)), поскольку в силу симметрии кривой кривизна в двух противоположных вершинах эллипса будет такой же.

Для расчета кривизны удобно перейти от канонического уравнения эллипса к уравнению в параметрической форме : \[x = a\cos t,\;\;\;y = b\sin t.\] где \(t\) − параметр. В точке \(A\left( \right)\) параметр имеет значение \(t = 0,\) а в точке \(B\left( <0,b>\right)\) его значение равно \(t = \large\frac<\pi ><2>\normalsize.\)

Данная функция достигает максимума в точках \(x = \large\frac<<2\pi n>>\normalsize,\;n \in Z.\) В силу периодичности кривизна во всех точках максимума одинакова, поэтому достаточно рассмотреть лишь точку \(x = 0\).

В данном случае точка \(x = 0\) является точкой перегиба функции \(y = \arctan x.\) Поскольку в точке перегиба вторая производная равна нулю, то кривизна здесь также должна быть равна нулю, что и показывает полученное решение.

Экспоненциальная функция \(y = \) − это единственная уникальная функция, у которой производные любого порядка равны самой функции. Поэтому для кривизны данной кривой можно сразу написать следующую формулу: \[ \right|>> <<<<\left[ <1 + <<\left( \right)>^2>> \right]>^<\large\frac<3><2>\normalsize>>>> > = <\frac<<>><<<<\left( <1 + >> \right)>^<\large\frac<3><2>\normalsize>>>>.> \] Знак модуля в числителе опущен, поскольку экспоненциальная функция всегда положительна.

Источник

Кривизна и её вычисление

Вы будете перенаправлены на Автор24

Основная формула для вычисления кривизны плоской кривой

Кривизна представляет собой количественную характеристику степени изогнутости плоской кривой.

Вычисление кривизны плоской кривой

Задачи вычисления кривизны плоской кривой.

\[y’=\left(2\cdot x^ <2>\right)^ <<'>> =4\cdot x; y»=\left(4\cdot x\right)^ <<'>> =4. \]

Подставляем полученные выражения в формулу для кривизны:

Подставляем полученные выражения в формулу для кривизны:

Готовые работы на аналогичную тему

\[x’_=\left(2\cdot \cos \left(3\cdot t\right)\right)^ <<'>> _=-6\cdot \sin \left(3\cdot t\right);\] \[x»_ =\left(-6\cdot \sin \left(3\cdot t\right)\right)^ <<'>> _=-18\cdot \cos \left(3\cdot t\right);\] \[y'_=\left(3\cdot \sin \left(2\cdot t\right)\right)^ <<'>> _=6\cdot \cos \left(2\cdot t\right);\] \[y''_ =\left(6\cdot \cos \left(2\cdot t\right)\right)^ <<'>> _=-12\cdot \sin \left(2\cdot t\right).\]

\[x'_\left(\frac<\pi > <6>\right)=-6\cdot \sin \left(3\cdot \frac<\pi > <6>\right)=-6;\] \[x''_ \left(\frac<\pi > <6>\right)=-18\cdot \cos \left(3\cdot \frac<\pi > <6>\right)=0;\] \[y'_\left(\frac<\pi > <6>\right)=6\cdot \cos \left(2\cdot \frac<\pi > <6>\right)=3;\] \[y''_ \left(\frac<\pi > <6>\right)=-12\cdot \sin \left(2\cdot \frac<\pi > <6>\right)=-6\cdot \sqrt <3>.\]

Полученные значения подставляем в формулу для кривизны:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 30 11 2021

Источник

СОДЕРЖАНИЕ

История

В Tractatus de configurationibus qualitatum et motuum философ и математик XIV века Николь Орем вводит понятие кривизны как меры отклонения от прямолинейности; для кругов кривизна обратно пропорциональна радиусу; и он пытается распространить эту идею на другие кривые с постоянно меняющейся величиной.

Плоские кривые

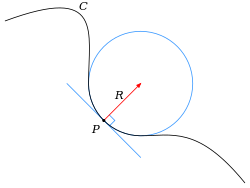
Оскулирующий круг

Этим определением сложно манипулировать и выразить его формулами. Поэтому были введены другие эквивалентные определения.

С точки зрения параметризации длины дуги

‖ γ ′ ‖ знак равно Икс ′ ( s ) 2 + у ′ ( s ) 2 знак равно 1. <\ displaystyle \ | <\ boldsymbol <\ gamma>> '\ | = <\ sqrt + y '(s) ^ <2>>> = 1.>

Это означает, что касательный вектор

Более того, поскольку радиус кривизны

С точки зрения общей параметризации

При такой параметризации кривизна со знаком равна

Они могут быть выражены безкоординатным образом как

и, таким образом, принимая норму обеих сторон

График функции

Поскольку первая и вторая производные от x равны 1 и 0, предыдущие формулы упрощаются до

для кривизны, и для

для подписанной кривизны.

В физике и технике принято аппроксимировать кривизну второй производной, например, в теории пучков или для вывода волнового уравнения натянутой струны, а также в других приложениях, где используются небольшие уклоны. Это часто позволяет системы, которые в противном случае нелинейными следует рассматривать как линейные.

Полярные координаты

Это следует из формулы для общей параметризации с учетом параметризации

Неявная кривая

Вышеупомянутая формула для кривизны может быть получена из выражения кривизны графика функции с помощью теоремы о неявной функции и того факта, что на такой кривой выполняется

Примеры

Может быть полезно проверить на простых примерах, что разные формулы, приведенные в предыдущих разделах, дают одинаковый результат.

Это параметризация длины дуги, поскольку норма

равно единице. Эта параметризация дает одно и то же значение кривизны, поскольку оно равно делению на r 3 как в числителе, так и в знаменателе в предыдущей формуле.

Парабола

Формулы Френе – Серре для плоских кривых.

Космические кривые

Как и в случае кривых в двух измерениях, кривизна кривой C регулярного пространства в трех измерениях (и выше) представляет собой величину ускорения частицы, движущейся с единичной скоростью по кривой. Таким образом, если γ ( s ) является параметризацией C длиной дуги, то единичный касательный вектор T ( s ) задается формулой

Общие выражения

κ знак равно ‖ γ ′ × γ ″ ‖ ‖ γ ′ ‖ 3 <\ displaystyle \ kappa = <\ frac <\ | <\ boldsymbol <\ gamma>> '\ times <\ boldsymbol <\ gamma>>' '\ |> <\ | <\ boldsymbol <\ gamma>>' \ | ^ <3>>>>

Здесь T обозначает матрицу, транспонированную вектора. Эта последняя формула (без перекрестного произведения) также верна для кривизны кривых в евклидовом пространстве любой размерности.

Кривизна от длины дуги и хорды

Поверхности

Кривизна кривых, нарисованных на поверхности, является основным инструментом для определения и изучения кривизны поверхности.

Кривые на поверхностях

Основная кривизна

Нормальные разделы

Гауссова кривизна

Гауссова кривизна является внутренним свойством поверхности, то есть не зависит от конкретного вложения поверхности; интуитивно это означает, что муравьи, живущие на поверхности, могут определять гауссову кривизну. Например, муравей, живущий на сфере, может измерить сумму внутренних углов треугольника и определить, что он больше 180 градусов, подразумевая, что пространство, в котором он обитает, имеет положительную кривизну. С другой стороны, муравей, живущий на цилиндре, не обнаружит такого отклонения от евклидовой геометрии ; в частности, муравей не смог обнаружить, что две поверхности имеют разную среднюю кривизну (см. ниже), что является чисто внешним типом кривизны.

Средняя кривизна

Вторая фундаментальная форма

Внутренняя и внешняя кривизна поверхности может быть объединена во второй фундаментальной форме. Это квадратичная форма в касательной плоскости к поверхности в точке, значение которой в конкретном касательном векторе X к поверхности является нормальной составляющей ускорения кривой вдоль касательной к X поверхности ; то есть это нормальная кривизна кривой, касательной к X (см. выше ). Символично,

Таким образом, вторая фундаментальная форма кодирует как внутреннюю, так и внешнюю кривизну.

Оператор формы

Для поверхности с касательными векторами X и нормалью N оператор формы может быть компактно выражен в обозначении суммирования индексов как

(Сравните альтернативное выражение кривизны для плоской кривой.)

Уравнения Вейнгартена дают значение S через коэффициенты первой и второй фундаментальных форм как

Искривление пространства

Расширяя предыдущий аргумент, пространство трех или более измерений может быть искривлено по своей сути. Кривизна является внутренней в том смысле, что это свойство, определенное в каждой точке пространства, а не свойство, определенное по отношению к большему пространству, которое его содержит. В общем, искривленное пространство может или не может быть задумано как встроенное в многомерное окружающее пространство ; в противном случае его кривизну можно определить только внутренне.

Обобщения

Математическое понятие кривизны также определяется в гораздо более общем контексте. Многие из этих обобщений подчеркивают различные аспекты кривизны, как это понимается в более низких измерениях.

Источник