Круги эйлера что значит
Круги Эйлера — примеры и методы решения логических задач
Круги Эйлера (другое название — диаграммы Венна) — это геометрическая схема, которую можно применять для наглядного отображения отношений между множествами. Диаграммы разработал известный математик и механик, чьим именем и назван метод. Учёный считал, что его подход облегчает размышления человека.
Множества в математике
Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:
Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.
В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:
Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.
Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.
Отношения между понятиями
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.
Рисунок 1
Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:
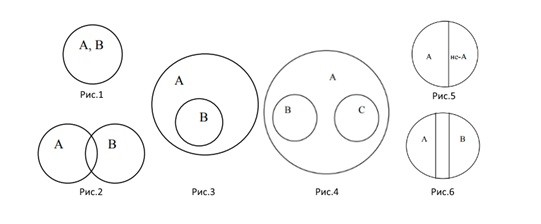
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.
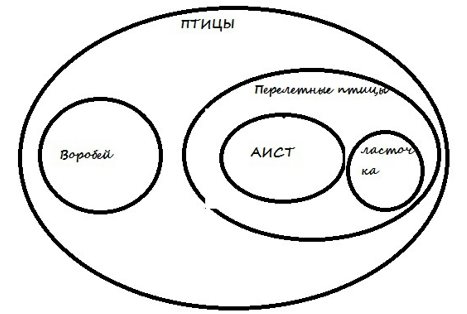
Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».
Несовместимыми называют понятия, не имеющие общих элементов:
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.
Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).
Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.
Решение задач, примеры
Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?
Рисунок 2
Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.
Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…
Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.
Рисунок 3
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.
Рисунок 4
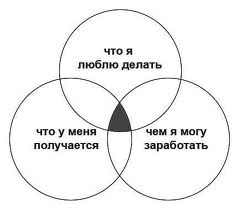
Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.
Круги эйлера что значит
Задачи для решения учащимися
1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:
а) не являются читателями школьной библиотеки;
б) не являются читателями районной библиотеки;
в) являются читателями только школьной библиотеки;
г) являются читателями только районной библиотеки;
д) являются читателями обеих библиотек?
2.Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе?
3.На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа.
4. В группе туристов 25 человек. Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?
6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?
7. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет. Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор? Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
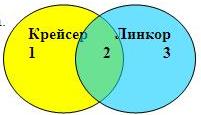
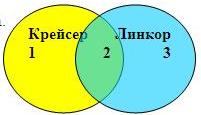
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Торты | Пироги | 12000 |
| Торты & Пироги | 6500 |
| Пироги | 7700 |
Какое количество страниц (в тысячах) будет найдено по запросу Торты?
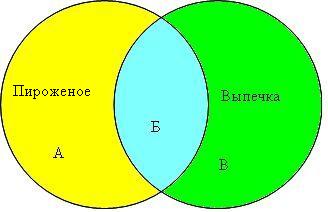
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Из условия задачи следует:
Торты │Пироги = А + Б + В = 12000
Торты & Пироги = Б = 6500
Пироги = Б + В = 7700
Сектор А равен 4300, следовательно
Торты = А + Б = 4300+6500 = 10800
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросуВыпечка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А + Б = 9700
Пироженое │ Выпечка = А + Б + В = 14200
Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 = 9600
Преобразим условие задачи в виде суммы секторов:
с паниели │(терьеры & овчарки) = Г + Б
с паниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
| 1 | барокко | классицизм | ампир |
| 2 | барокко | (классицизм & ампир) |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Для решения задачи представим запросы в виде кругов Эйлера.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
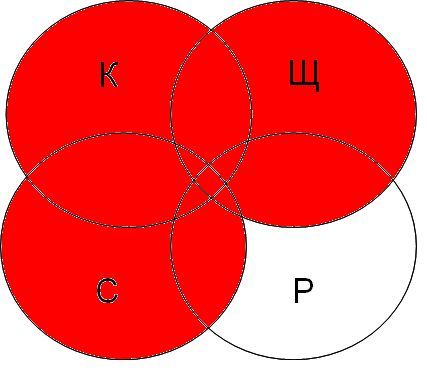 | 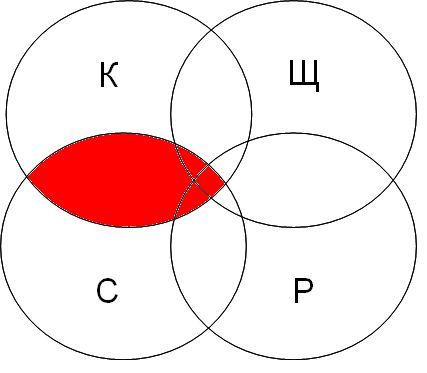 | 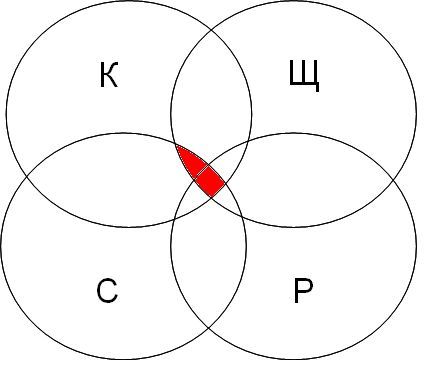 | 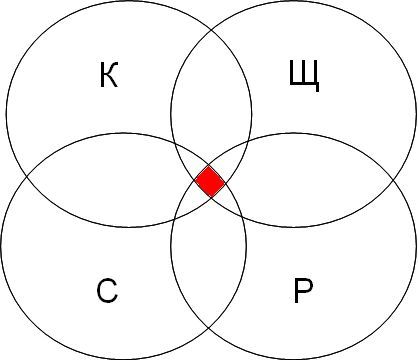 |
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Разбор задачи B12 (демо ЕГЭ 2012)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
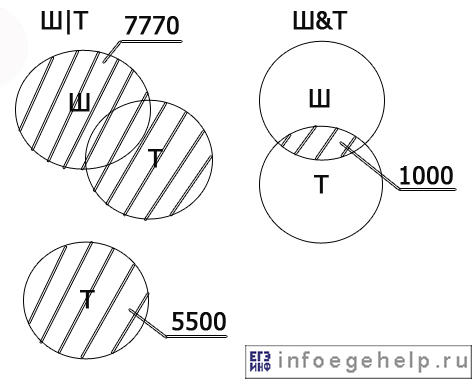
| Шахматы | Теннис | 7770 |
| Теннис | 5500 |
| Шахматы & Теннис | 1000 |
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Задачи для самостоятельного решения
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Круги Эйлера
Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.
Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.
Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы «Нейробика».
Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
Есть несколько групп кругов Эйлера:
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Типичный пример кругов Эйлера
Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:
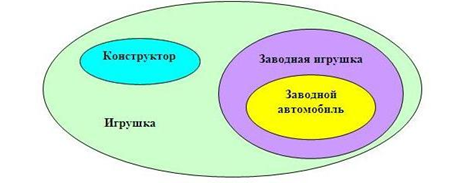
На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.
Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.
По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).
Пример решения задачи с помощью кругов Эйлера
Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.
Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:
Учитывая условия задачи, составляем уравнения:
Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим:
4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).
Далее полученный результат подставляем в уравнение 3 и получаем:
2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).
Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.
Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.
Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.