Круглые числа что это такое 3 класс
Учимся вместе: математика
Выпуск № 31 от 2009-09-01
www.clearwords.ru
Количество человек, получивших этот выпуск: 563
Цитата
Круглое число
В математике определенные группы чисел имею свои названия. Это сделано для удобства классификации разного рода чисел. Так, мы уже рассматривали группу чисел, а именно четные и нечетные числа. Теперь рассмотрим еще одну категорию чисел, которая имеет свое название.
Мы рассмотрим группу чисел, которая называется – «круглые числа». Чтобы понять, что такое круглое число, давайте возьмем реальные предметы, например, количество домов в городе. Это количество может быть 23, 234, 500, 534, 700, 800, 957. Чем больше город, тем больше количество домов. Но нас сейчас интересует сам вид представленных чисел. Если вы внимательно посмотрите, то увидите, что среди перечисленных выше чисел, есть числа, которые по виду явно отличаются от других. Это числа 500, 700 и 800.
Такие числа называются круглыми числами.
Определение
Таким образом, круглым называется число, которое делится на 10, 100, 1000 и так далее, без остатка. Можно так же круглое число определить как число, которое имеет один и более нулей в правой части числа. Слева может быть любое число, а справа один или более нулей.
Вот примеры чисел, которые называются круглыми: 200, 300, 400, 500, 600, 700, 800, 4300.
Примеры использования
Круглое число легко можно узнать по нулям в правой части числа.
Задание
Составьте сами несколько предложений с этим словом, чтобы до конца усвоить его.
В следующих уроках мы рассмотрим и другие слова, которые используются в математике. Шаг за шагом мы с вами разберем все основные слова, и вам станет многое понятно в этой науке, и она перестанет быть чем-то запутанным и сложным.
Отзывы после просветительской кампании «Проясняй слова, Россия!»
Проблема, затронутая участниками форума является актуальной. Самое главное в учебном процессе, это непосредственное желание обучаться. Углубление и прояснение причины нежелания учиться необходимо. Необходимо научить учителей учить детей правильно, воспитывать ребенка в любви к обучению и самообучению.
Числа от 1 до 100. Состав числа. Круглые числа
Числа от 1 до 100
Предыдущее и последующее число
56 , 57
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Состав двузначного числа
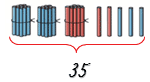
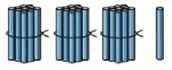
Всего на рисунке 35 палочкек.
35 = 30 + 5
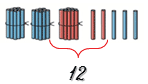
Красных палочек 12.
12 = 10 + 2
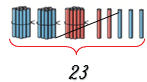
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
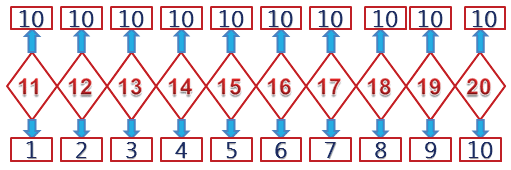
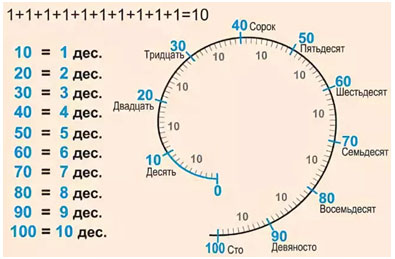
Круглые числа
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
10 + 40 = 50
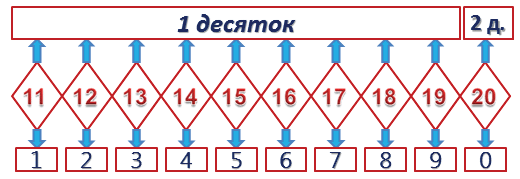
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:
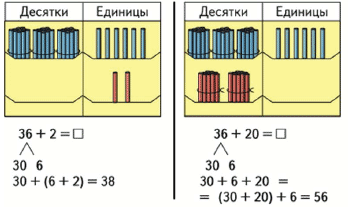
Действия с десятками и единицами
Как решить пример 34 + 25?
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
Можно рассуждать так:
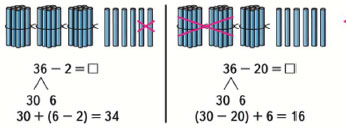
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
Поясните, пожалуйста!
Поясните, пожалуйста, как выполнить задание: «Подчеркните числа, в которых число сотен «круглое»:500,20000,7020,70000, 600,100,21000,1000,1020,800,80000.
Тэги: Уважаемые, коллеги, работающие по учебнику математики Чекина 3
Надо подчеркнуть КРУГЛОЕ число СОТЕН, а не просто круглое число.
Действительно:
— в числе (из примера) 20000 число СОТЕН = 200. Это ЦЕЛОЕ ЧИСЛО. Оно делится на 100 без остатка. В результате его деления на 100 получается ЦЕЛОЕ число;
— в числе (из примера) 500 число сотен = 5. Это число не делится на 100 без остатка и в результате его деления на 100 не получается целое число.
`Первый, раскладывая кусочки бумаги на колене,
при каждом обрезке повторял наре, наре (один);
другой повторял слово наре и загибал при этом палец
прежде на одной, затем на другой руке.
Насчитав до десяти и согнув пальцы обеих рук,
опустил оба кулака на колени проговорив:`две
руки`, причем третий папуас загнул палец руки.
Со вторым десятком было сделано то же,
причем третий папуас загнул второй палец;
то же самое было сделано для третьего десятка;
оставшиеся бумажки не составляли четвёртого
десятка и продолжали лежать в стороне`.
Деньги все хорошо считают.
Моя бабушка хоть и закончила 1 или 2 класса деревенской школы при проклятом царизме,
а деньги на базаре считать умела.
Это я про тех, кто `изобретает` такие задания.
Ладно бы, если б речь шла о чём-то стояшем.
А то полдня идёт разговор ни о чём.
Чтобы решить эту задачу правильно и доступно для третьеклассника,
да ещё чтобы вышел какой-то методический толк,
надо сначала исходные числа перевести в сотни:
а потом уже рассуждать о круглости.
А без этого получилось, что ищут круглое число
килограммов в целом числе центнеров.
Поэтому, хотя толк-то куда-то и вышел,
зато бестолочь вся на месте осталась.
Весь спор и идет вокруг определения `круглое` число
Александр Владимирович утверждает:
`круглое` = `целое`
Марина Осиповна дает опроеделение:
`круглое` = `число заканчивающееся нулем`
Прокомментируйте!
Выскажите Ваше мнение:

Вакансии для учителей
Круглые числа
Кру́глыми чи́слами относительно некоторой позиционной системы счисления называют степени её основания. В этой системе счисления такие числа записываются как единица с последующими нулями. Количество нулей справа от единицы равно показателю степени основания.
Примеры
Обобщения
Иногда понятие круглого числа расширяют до всех чисел, являющихся произведением базового числа (такого, которое можно записать одной цифрой) и степени основания, например, 400010=410 × 100010, 6000008=68 × 1000008, 203=23 × 103. В записи такого числа есть одна ненулевая цифра с левого края и несколько нулей справа от неё.
Ещё шире круглое число можно определять как всякое число кратное степени основания системы счисления, то есть достаточно присутствия одного или нескольких нулей с правого края, например, 45600010=45610 × 100010, 3405=345 × 105, 1001002 = 10012 × 1002. В такой трактовке понятия для любого составного числа с помощью факторизации можно найти систему счисления, в которой это число будет круглым. Например, число 3410 = 17 × 2 является круглым в любой системе счисления, основание которой равно одному из делителей числа. В данном случае 3410=1000102=2017.
Полезное
Смотреть что такое «Круглые числа» в других словарях:
Круглые числа всегда лгут — Слова английского писателя и лексикографа Сэмюэля Джонсона (1709 1784). Иносказательно: сомнение в истинности какой либо информации, подкрепленной подозрительно круглыми числами. Энциклопедический словарь крылатых слов и выражений. М.: «Локид… … Словарь крылатых слов и выражений
КЛАСС НЕМАТОДЫ или КРУГЛЫЕ ЧЕРВИ (NEMATODA) — Если бы тип немательминтов был ограничен только рассмотренными выше классами животных, то едва ли была бы построена та общая характеристика этого типа, которая возникла в современной науке. Кроме того, его значение и в экономике природы … Биологическая энциклопедия
Центрированные шестиугольные числа — – это центрированные фигурные числа, которые представляют шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке. 1 7 19 37 +1 +6 +12 +18 … Википедия
Список чисел — Содержание 1 Натуральные числа 1.1 от 1 до 2099 1.2 «Круглые» числа от 200 до 10000 1.3 Степени двойки … Википедия
Правила округления — Округление математическая операция, позволяющая уменьшить количество знаков в числе за счёт замены числа его приближённым значением с определённой точностью. Содержание 1 Методы округления 1.1 Варианты округления к ближайшему целому … Википедия
Круглое число — Круглыми числами относительно некоторой позиционной системы счисления называют степени её основания. В этой системе счисления такие числа записываются как единица с последующими нулями. Количество нулей справа от единицы равно показателю степени… … Википедия
Катерхэм (команда Формулы-1) — Caterham … Википедия
Рамануджан, Сриниваса Айенгор — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Рамануджан — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Рамануджан, Сриниваса — Один из немногих известных портретов С. Рамануджана Рамануджан Сриниваса Айенгор (Ramanujan) (22 декабря 1887, Ироду на юге Индии, 26 апреля 1920, близ Мадраса) индийский математик. Не имея специального математического образования, получил… … Википедия
Круглые числа что это такое 3 класс
Занимательная математика
Навигация
Полезные ссылки
Круглые числа
При каждой переписи населения обычно наблюдается чрезмерное обилие людей, возраст которых оканчивается на 5 или на 0; их гораздо больше, чем должно бы быть. Причина кроется, конечно, в том, что люди не помнят, твердо, сколько им лет и, показывая возраст, невольно «округляют» годы. Замечательно, что подобное же преобладание «круглых» возрастов наблюдается и на могильных памятниках древних римлян.
Эта одинаковость числовых пристрастий идет еще дальше. Один германский психолог (проф. К. Марбе) подсчитал, как часто встречается в обозначениях возраста на древне-римских могильных плитах та или иная цифра, и сравнил эти результаты с повторяемостью цифр в обозначениях возраста по переписи в американском штате Алабама, где живут преимущественно негры (примечание редактора: сохранено оригинальное слово из книги, хотя в наше время более политкорректно говорить «афроамериканец»). Получилось удивительное согласие: древние римляне и современные нам негры до малейших подробностей сходятся в числовых пристрастиях! Конечные цифры возраста, по частоте их повторяемости, располагались в обоих случаях в одинаковой последовательности, а именно:
0, 5, 8, 2, 3, 7, 6, 4, 9 и 1.
Но и это не все. Чтобы выяснить числовые пристрастия современных европейцев, упомянутый ученый производил такого рода опыты: он предлагал множеству лиц определить «на-глаз», сколько миллиметров заключает в себе полоска бумаги, например, в палец длиною, и записывал ответы. Подсчитав затем частоту повторения одних и тех же конечных цифр, ученый получил снова тот же самый ряд:
0, 5, 8, 2, 3, 7, 6, 4, 9 и 1.
Нельзя считать случайностью, что народы, столь отдаленные друг от друга и антропологически, и географически, — обнаруживают полную одинаковость числовых симпатий, т. е. явное пристрастие к «круглым» числам, оканчивающимся на 0 или 5, и заметную неприязнь к числам некруглым.
Любовь к пятеркам и десяткам находится, без сомнения, в прямой связи с десятичным основанием нашей системы счисления, т.е. в конечном итоге — с числом пальцев на обеих руках. Остается неразгаданной лишь та правильность, с какой слабеет эта симпатия по мере удаления от 5 и 10.
Это пристрастие к округленным числам обходится нам, надо заметить, довольно дорого. Товарные цены в розничной продаже всегда тяготеют к этим круглым числам: некруглое число, получающееся при исчислении продажной стоимости товара, дополняется до большего круглого числа. Цена книги редко бывает 57 коп., 63 коп., 84 коп., — а чаще 60 коп., 65 коп., 85 коп. Но округленность цены достигается обычно за счет покупателя, а не продавца. Общая сумма, которую потребители переплачивают за удовольствие приобретать товары по круглым ценам, накопляется весьма внушительная. Кто-то дал себе труд, задолго до последней войны, приблизительно подсчитать ее, и оказалось, что население прежней России ежегодно переплачивало в виде разницы между круглыми и некруглыми товарными ценами не менее 30 миллионов рублей. Не слишком ли дорогая дань невинной слабости к округлениям?
Источник: Я.И. Перельман. Занимательная арифметика. «Время» 1926.