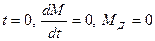Крутильная жесткость в чем измеряется

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Источник

Дополнительным понятием является гибкость или податливость: чем более гибкий объект, тем он менее жесткий.

СОДЕРЖАНИЕ

Расчеты

Следует отметить, что для тела с несколькими степенями свободы вышеупомянутое уравнение обычно не применяется, поскольку приложенная сила создает не только отклонение в его направлении (или степени свободы), но также и отклонение в других направлениях.

Для тела с несколькими степенями свободы, чтобы вычислить конкретную прямую жесткость (диагональные члены), соответствующая степень свободы остается свободной, а остальная часть должна быть ограничена. При таком условии вышеприведенное уравнение может получить прямую жесткость для степени неограниченной свободы. Соотношения между силами реакции (или моментами) и произведенным прогибом представляют собой жесткости соединения.

Согласие

Вращательная жесткость

На аналогичной основе выводятся и другие меры жесткости, в том числе:

Отношение к эластичности

Точно так же жесткость прямого участка на кручение равна

Обратите внимание, что жесткость на кручение имеет размеры [сила] * [длина] / [угол], так что ее единицами СИ являются Н * м / рад.

В частном случае неограниченного одноосного растяжения или сжатия модуль Юнга можно рассматривать как меру жесткости конструкции.

Приложения

Жесткость конструкции имеет принципиальное значение во многих инженерных приложениях, поэтому модуль упругости часто является одним из основных свойств, учитываемых при выборе материала. Высокий модуль упругости требуется, когда отклонение нежелательно, в то время как низкий модуль упругости требуется, когда требуется гибкость.

Источник

2.4.5.2 Продольная, поперечная и крутильная жесткость

Продольная, поперечная и крутильная жесткость

Определение жесткости на изгиб в качестве входного параметра для нелинейного расчета описано в предыдущих главах. Остальные параметры жесткости можно определить следующим образом.

Как и в случае с изгибом, продольная жесткость E ⋅ A определяется из коэффициента деформации ε ₀ действующей осевой силы. При одновременном изгибном моменте и осевой силе, это более не возможно применить непосредственно, потому что это приведет к отрицательной жесткости в конкретных областях при условии, что подход будет выполняться последовательно. Это вытекает из упрощенного расчета без учета сдвига нейтральной оси для деформации. При выполнении нелинейных расчетов, эта ось больше не совпадает с центром тяжести сечения. Как правило, это можно учесть, расчленяя матрицу жесткости от центра тяжести. Тем не менее, это приведет к прямой корреляции между моментом и осевой силой в терминах матрицы жесткости. RF-CONCRETE Стержни не учитывают деформацию осей из-за образования трещин или физической нелинейности.

Рассматривая связь между осевой силой и изгибающим моментом, мы можем видеть прямую корреляцию между обе коэффициентами жесткости. Для пояснения, представьте себе столбец с постоянной степенью сжатия: Если увеличивающийся момент действует в дополнение к осевой силе, кривизна, ведущая к смещению полученной осевой силы от центра тяжести, будет добавлена к диаграмме чистой постоянной деформации. Таким образом, с пластической точки зрения, соответственно уменьшается полезная площадь результирующей силы, что по необходимости приводит к большим деформациям и, следовательно, к уменьшению жесткости. Таким образом, практическое решение является приблизительным учетом аффинности между жесткостью на изгиб и жесткостью на изгиб в случае изгиба с осевой силой.

Определение жесткости при сдвиге в деталях очень сложно для проектирования железобетонных конструкций, и это работа, которая едва ли может быть решена в отношении различных геометрических схем и схем нагрузок. Теория пучка быстро достигает своих пределов, потому что несущая способность должна определяться эффектом фермы, чтобы представить жесткость при умеренной нагрузке сдвига. В прошлом такие модели использовались для разработки различных методов, которые обычно не являются или лишь частично достаточны для их применения.

В упрощенном методе, Pfeiffer [8] уменьшает жесткость при сдвиге в соответствии с доступной жесткостью на изгиб. Даже если этот подход представляется вначале несколько странным, это результат простой идеи, который является простым и правдоподобным. Представьте себе, что изгибная нагрузка и напряжение сдвига являются независимыми. При просмотре измененной нагрузки момента и осевой силы, изгибная жесткость изменяется в соответствии с диаграммой деформации и кривизны. Тем не менее, это не только влияет на жесткость в продольном направлении балки, но и в поперечном направлении, используемом для передачи поперечных сил.

Данный подход подразумевается в качестве приближения, которое предполагает достаточную пропускную способность, но не (или только грубо) определяет наклонные трещины, увеличение растягивающей силы и т.д. Несмотря на эти упрощения, метод по Pfeiffer для умеренно тонких балок можно считать достаточно точным подходом. В качестве альтернативы, можно также взять линейную упругую жесткость сдвига в качестве основы для расчета в RF-CONCRETE-стержнях.

По сравнению с изгибной жесткостью, жесткость при кручении сильно уменьшается в случае трещин. С одной стороны, это является положительным, поскольку моменты кручения от сдерживания, которые часто возникают в конструкции здания, почти полностью уменьшены для приращений нагрузки до тех пор, пока не будет достигнута ошибка. С другой стороны, имеется так называемое равновесное кручение, в котором сильное снижение крутильной жесткости может уже приводить к замечательным кручениям в состоянии пригодности к эксплуатации и, следовательно, к снижению работоспособности.

Pисунок 2.27 Рисунок из [9] о снижении крутильной жесткости в случае взлома

Существуют два различных подхода для учета жесткости при кручении, доступных для расчета с RF-CONCRETE-стержнями.

Для жесткости при кручении в состоянии I, программа учитывает, что жесткость уменьшается на 30 и 35% до достижения момента трещины. Причины, обозначенные Леонхардтом, следующие: железобетонный стержень выходит из нагрузки, а напряжения смещаются наружу. В некоторой степени также участвует образование трещин.

Жесткость при кручении в состоянии II определяется из модели пространственных ферм. Для упрощения, можно предположить, что наклон сжатия будет ниже 45 °. По мнению Леонхардта, это предположение верно также, когда коэффициенты продольной и поперечной арматуры не равны. Незначительные наклоны расположений являются результатом анализа равновесия или расчетного допущения, если коэффициент армирования звеньев меньше, чем у продольной арматуры. Тем не менее, испытания показали, что предполагаемый наклон улочка стержня возникает только при высоком напряжении.

Тесты также показали, что модель фермы представляет собой хороший алгоритм для определения крутильного напряжения для предела сбоя. Тем не менее, для состояния работоспособности, мы можем заметить, что стальные напряжения в сдвиге и продольной арматуре не достигают значений в соответствии с аналогией фермы даже после нескольких повторений нагрузок.

G c · I T x I I = 4 E s · A k 3 u k 2 · 1 k T 1 μ L + 1 μ Bü + 4 α · A k u k · t · 1 + φ

G c · I T x I I = E s · A k 2 · t u k 2 · 1 k T μ Bü + α 4 · 1 + φ

для наклона на сжатие 90 °

для наклона на сжатие 45 °

продольный коэффициент армирования, связанный с керном

коэффициент поперечной арматуры, связанный с керн

Определение момента трещины для сечений твердых тел:

Определение момента трещины для полого сечения:

крутящий момент, для которого статическое напряжение в модели фермы достигает предела текучести (крутящий момент, который может быть поглощен)

момент кручения для перехода в состояние II (момент трещины)

площадь, окруженная осевой линией стен

площадь поперечного сечения продольной арматуры

площадь поперечного сечения сдвиговой арматуры

Соотношения модулей упругости E _s / E _c

периметр площади A _k

расстояние между звеньями

эффективная толщина стенки

коэффициент ползучести ₓ

Не будет достигнуто взаимное влияние жесткости на изгиб и изгиб.

В качестве альтернативы, можно рассчитывать с линейной упругой жесткостью при кручении, которая уменьшается в процентах в области трещины.

Часто посещаемые страницы

Dlubal Software GmbH
Am Zellweg 2
93464 Tiefenbach
Германия

Источник

Сила упругости

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

Сила упругости: Закон Гука

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, про­порциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Закон Гука

Fупр = kx

Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

Тогда из Закона Гука выразим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

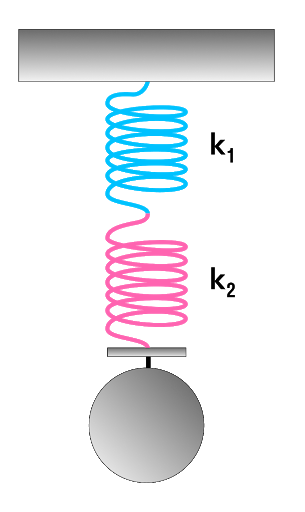
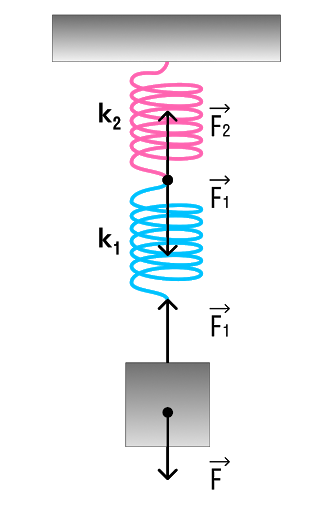
Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k_i

k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

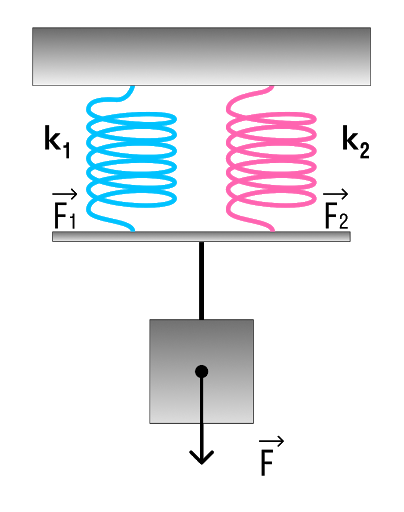
Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

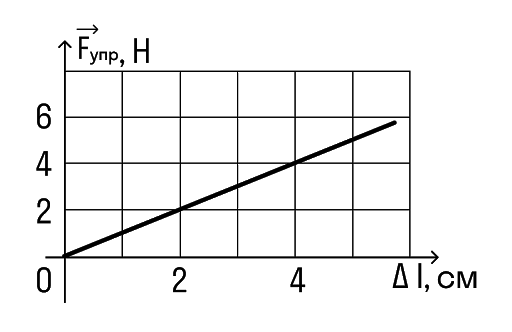
Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Задачка 2

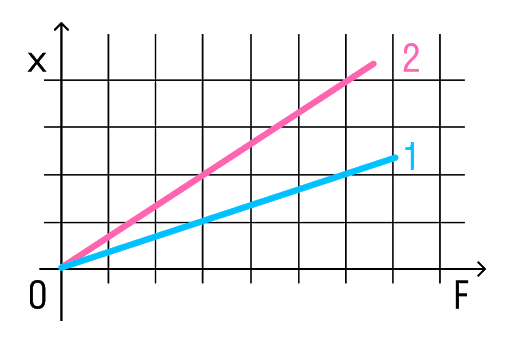
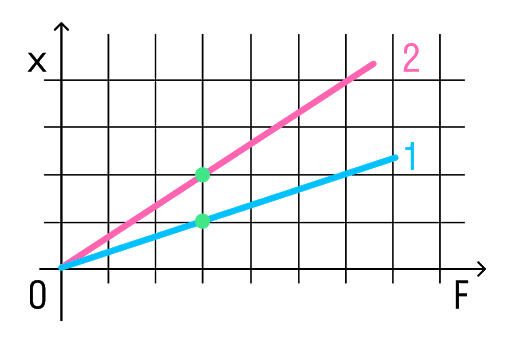
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

Источник

Продольная жесткость стержня

Жесткость канатного полиспаста

,

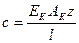
где Ек = 1,2×10 11 Па — модуль продольной упругости каната; Ак — площадь поперечного сечения проволок каната; z — число ветвей полиспаста; l — длина полиспаста.

Поперечная жесткость балок зависит от способа закрепления и приведена в курсах сопротивления материалов. Например, жесткость консольной балки

, (2.17)

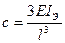
где I_Э — экваториальный момент инерции сечения, м 4 ; l — длина балки, м.

Крутильная жесткость характеризуется коэффициентом жесткости с при кручении, представляющем собой крутящий момент М_КР, закручивающий вал на угол j = 1 рад (Н×м/рад):

Жесткость круглого вала

,

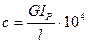
где 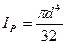— полярный момент инерции сечения вала диаметром d; l — длина закручиваемого участка вала.

При расчетах более удобно пользоваться коэффициентом податливости (в дальнейшем будем называть податливостью). Общая податливость детали равна сумме податливостей отдельных ее участков.

Расчет динамических нагрузок в упругих связях для различных случаев нагружения. После расчета параметров приведенной системы определяем динамические нагрузки в упругих связях механизмов.

Рассмотрим динамические нагрузки в двухмассовой системе с линейной жесткостью с и массами m₁ и m₂, на которые действуют силы движущие F и вес груза G (рисунок 2.2). К такой системе можно привести механизмы подъема, где жесткость канатов полиспастов намного меньше жесткости самого привода, ленточные и цепные конвейеры и др.

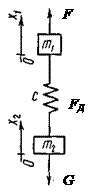Рисунок 2.2 – Эквивалентная двухмассовая схема механизма

Под действием внешних сил в неустановившийся период в упругой системе возникают колебательные процессы, которые можно описать следующей системой дифференциальных уравнений движения масс:

(2.19)

где х₁, х₂ — перемещение соответственно первой и второй масс.

Силу G берут со знаком «минус» как силу сопротивления.

В уравнениях (2.19) первые слагаемые — силы инерции соответствующей массы, вторые — силы упругости в связи; в правой части уравнений — силы, действующие на систему в период неустановившегося движения.

Умножив первое уравнение (2.19) на m₂, второе — на m₁ вычтя второе из первого и разделив на m₁m₂, получим

(2.20)

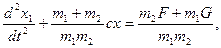
Дифференциальное уравнение (2.20) характеризует деформацию упругого звена или динамическое усилие в нем при условии, что

(2.21)

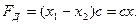
Решив уравнение (2.20) и учитывая условие (2.21), получим уравнение для определения динамических усилий в упругой связи:

(2.22)

(2.23)

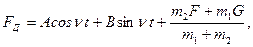
Период собственных колебаний

(2.24)

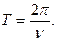
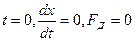
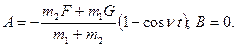
Постоянные А и В находят из начальных условий. При нулевых условиях ( ) постоянные будут:

(2.25)

Подставив постоянные А и В в уравнение (2.21), получим формулу для определения динамических усилий в упругой связи:

(2.26)

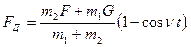
Обозначим постоянную составляющую нагрузок, равную сумме статических и инерционных (от массы m₂) нагрузок, через F_П:

(2.27)

где — коэффициенты распределения масс в системе.

Тогда уравнение (2.26) можно записать в таком простом виде:

(2.28)

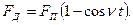
Для расчета динамики механизмов передвижения, поворота и других реальную систему целесообразно приводить к крутильной расчетной схеме (рисунок 2.3). Для двухмассовой системы дифференциальные уравнения движения масс, совершающих крутильные колебания, можно записать в виде:

(2.29)

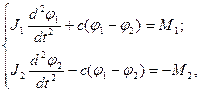
где J₁ — общий момент инерции вращающихся масс привода (ротора, тормозного шкива, муфт); J₂ — приведенный к валу двигателя момент инерции второй массы — поступательно и вращательно движущихся частей крана; j₁, j₂ — углы закручивания первой и второй масс; с — приведенная крутильная жесткость линии передач; М₁ — пусковой (тормозной) момент электродвигателя (тормоза); М₂ — момент сопротивления движению крана.

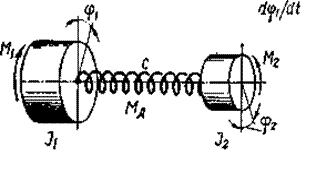Рисунок 2.3 – Эквивалентная двухмассовая крутильная схема механизма

Моменты инерции масс и силовые моменты необходимо привести к валу двигателя или ходовых колес.

При нулевых начальных условиях

момент сил упругости в линии передач привода

(2.30)

(2.31)

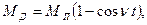
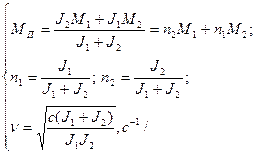
Аналогично можно определить – динамические нагрузки при торможении механизма, подставив вместо М₁ тормозной момент М_Т. Динамические нагрузки при торможении, как правило, больше, чем при пуске привода.

Из уравнения (2.31) следует, что максимальные моменты сил упругости в приводной линии равны удвоенному значению статических и инерционных нагрузок. Однако действительные системы механизмов многомассовые с зазорами в соединениях. Поэтому динамические нагрузки в их приводах во много раз превышают статические нагрузки от сил сопротивления. Особенно интенсивные колебания возникают в механизме при резких торможениях короткоходовым тормозом или при противовключении электродвигателя.

Дата добавления: 2018-11-26 ; просмотров: 3489 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник