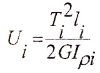Крутящий момент что это сопромат

изучаем сопротивление материалов

Определение крутящих моментов и построение эпюры

Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент M_к.

Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня.

Правило знаков для крутящих моментов.

Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.

Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.

где L_mн и L_mк – расстояние от начала координат до начала и до конца распределенного момента соответственно.

Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:

Общий порядок расчета и построения эпюры.

Построение эпюр крутящих моментов (пример)

Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами M_кв1=-30кН·м, M_кв2=50 кН·м, и распределенным моментом m₁=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).

1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.

2. Проведем сечение 1. Определим крутящий момент в текущем сечении:

3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом M_к2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:

3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:

4. Аналогично для сечения 4:

5. Также для сечения 5:

7. По полученным значения строим эпюру крутящих моментов (см. рис.).

Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) M_к6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.

Правила контроля правильности эпюр крутящих моментов

Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.

Дополнительно

Еще один вариант построения эпюры крутящих моментов с использованием компьютера найдете на этой странице.

1 В технике употребляется терминология «винт с правой резьбой» или «винт с левой резьбой». На винт с правой резьбой гайка навертывается при вращении по часовой стрелке (т.е прикладываем положительный момент M_к ), а свинчивание гайки происходит при вращении влево (т.е прикладываем отрицательный крутящий момент ).

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Понятие о вращающих и крутящих моментах

Часто в прикладных задачах механики прихо­дится определять моменты сил, приложенных к телу, относительно его оси. Покажем, что в сечениях тела под действием внешних сил всегда возникают внутренние силы.

Рассмотрим устройство для подъема грузов, состоящее из вала ABC, на который насажены барабан АВ с радиусом r и зубчатое колесо С с радиусом R.

Вал при­водится во вращение от электродвигателя D через зубчатую передачу. Вес поднимаемого груза Q передается через трос на обод барабана, а от шестерни K, насаженной на вал электродвигателя, передается движущая сила Р.

При равномерном подъеме груза моменты внешних сил, прило­женных к валу, должны уравновешиваться, т. е.

Реакции опор А и В не войдут в уравнение моментов, так как они пересекают ось z и, следовательно, не создают относительно этой оси моментов.

Из составленного уравнения равновесия следует, что PR = Qr или М_z (Р) = М_z (Q), т. е. на концы участка вала, расположенного между сечением приложения груза Q и зубчатым колесом С, действуют равные и проти­воположно направленные моменты внешних сил. Эти мо­менты называют вращающими моментами.

Участок вала между сечениями приложения вращаю­щих моментов, как уже отмечалось, находится в равно­весии. Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение Е.

Чтобы отсеченная часть ЕС находилась в равновесии, в сечении Е должен действовать какой-то момент, равный и противоположный по направле­нию вращающему моменту, приложенному к колесу С. Этот момент называется крутящим (его обозначают М_к ) и является моментом внутренних сил, возникающих в се­чении тела.

Использованный здесь метод установления внутрен­них сил в сечении вала называется методом сечений (более подробно о методе сечений — см. здесь).

Момент внутренних сил в сечении —крутящий мо­мент— равен алгебраической сумме моментов внешних сил, т. е. вращающих моментов, приложенных к отсечен­ной части вала:

где n — число вращающих моментов, приложенных к от­сеченной части рассматриваемого вала.

Знак крутящего момента в поперечном сечении вала можно установить, исходя из направления внешних вра­щающих моментов. Условимся считать крутящий момент положительным, когда внешние моменты, приложенные к валу, вращают отсеченную часть по часовой стрелке (если смотреть со стороны внешней нормали к проведенному се­чению). На рассматриваемом рисунке сила Р вызывает вращение отброшенной части вала против часовой стрелки, если смотреть со стороны внешней нормали на проведенное сечение Е. Таким образом, в рассмотренном сечении Е возникает отрицательный крутящий момент.

При возрастании веса поднимаемого груза соответственно увеличиваются вращающие моменты. Будут возрастать также крутящие мо­менты в сечениях вала. Очевидно, что при данных размерах вала нельзя допускать безграничного возрастания вращаю­щего, а следовательно, и крутящего моментов, так как вал может разрушиться или сильно деформироваться. По­этому определение крутящих моментов имеет очень боль­шое практическое значение для расчетов на прочность.

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Кручение

Внутренний крутящий момент в сечении вала М_к (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.

где М_i – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.

Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:

Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρ_max

Условие прочности по допускаемым напряжениям

где — это допускаемое касательное напряжение.

Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом

где G – модуль сдвига

Относительный угол закручивания (рад/м) для силового участка

Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде

Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.

В характерных точках сечения

угол закручивания на силовом участке вала

Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.

Касательные напряжения в характерных точках сечения

Угол закручивания на силовом участке вала

Кручение бруса тонкостенного замкнутого круглого сечения

Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:

Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:

Угол закручивания

Кручение пустотелых валов круглого сечения

Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.

Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:

Кручение бруса прямоугольного сечения

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).

Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,

Iк=β∙h∙b3 – момент инерции при кручении.

В этих формулах: b – меньшая из сторон прямоугольника,

h – большая сторона,

α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).

Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Значения коэффициента γ Запись опубликована 04.09.2014 автором admin в рубрике Кручение, Сопромат.

Источник

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

Источник

iSopromat.ru

Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.

Брусья, испытывающие кручение, принято называть валами.

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов m_i, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: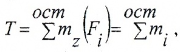

т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов m_i, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

Напряжения при кручении

В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: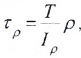

где I_ρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид: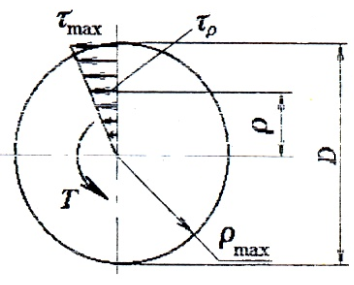

Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρ_max: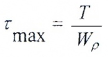

Здесь: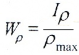

— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: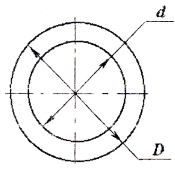


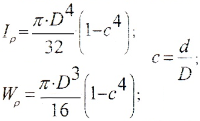
б) для вала сплошного сечения (c=0)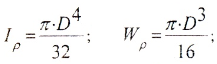

в) для тонкостенной трубы (t 0,9)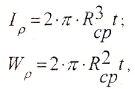

где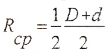

— радиус срединной поверхности трубы.

Деформации

Деформации валов при кручении заключаются в повороте одного сечения относительно другого.

Угол закручивания вала на длине Z определяется по формуле: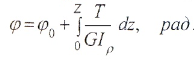

Если крутящий момент и величина GI_ρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: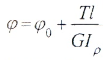

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: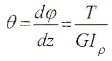

Расчет валов сводится к одновременному выполнению двух условий:

Для стальных валов принимается:

Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:

Из двух найденных значений крутящего момента необходимо принять меньшее.

Потенциальная энергия упругой деформации определяется по формуле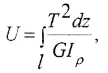

или для участка вала при постоянном T и GI_ρ

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник