Кто такие графы и что они делали
Граф (титул)
Граф (нем. Graf ) — королевское должностное лицо в Раннем Средневековье в Западной Европе. Титул возник в IV веке в Римской империи и первоначально присваивался высшим сановникам (например, comes sacrarum largitionum — главный казначей). Во Франкском государстве со второй половины VI века граф (гауграф) в своём округе-графстве/гау (нем. Gau — первоначально, сельская община у древних германцев, численностью ок. 100 человек) обладал судебной, административной и военной властью. По постановлению Карла II Лысого (877) должность и владения графа стали наследственными.
В период феодальной раздробленности — феодальный владетель графства, затем (с ликвидацией феодальной раздробленности) титул высшего дворянства (женщина — графиня). В качестве титула формально продолжает сохраняться в большинстве стран Европы с монархической формой правления.
В России титул введён Петром I (первым его получил в 1706 году Б. П. Шереметев). В конце XIX века учтено свыше 300 графских родов. Графский титул в советской России был ликвидирован Декретом ВЦИК и Совнаркома от 11 ноября 1917 года.
Содержание
История термина
См. также
Примечания
Литература
Полезное
Смотреть что такое «Граф (титул)» в других словарях:
Граф (титул) — Граф (нем. Graf, лат. comes, франц. cornte, англ. earl), в раннее средневековье в Западной Европе королевское должностное лицо (во Франкском государстве Г. обладал со 2 й половины 6 в. в своём округе графстве судебной, административной, военной… … Большая советская энциклопедия
Граф титул — (немецк. Graf; старинные формы garafio, grafio, gerefa, greve; франц. comte, от лат. comes; англ. earl) в настоящее время титул, первоначально название должностного лица во Франкском государстве и в Англии. Этимология слова graf очень неясна.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Граф, титул — (немецк. Graf; старинные формы garafio, grafio, gerefa, greve; франц. comte, от лат. comes; англ. earl) в настоящее время титул, первоначально название должностного лица во Франкском государстве и в Англии. Этимология слова graf очень неясна.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Варвик (граф. титул) — (Warwick) английский графский титул, который носили разные дома и который был соединен с владением замком В. Этот замок, один из древнейших в Англии, был, по преданию, еще во времена англосаксов жилищем знаменитого в английских героических… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ГРАФ — (нем. Graf). В средние века, в зап. Европе так наз. старейшины областей, производившие уголовный суд и обязанные, в случае войны, приводить отряд войска. Теперь граф титул высшего дворянства, не дающий никаких особенных прав. Словарь иностранных… … Словарь иностранных слов русского языка
Граф — Граф: От древневерхненемецкого gravo, gravio «предводитель, вождь»: Граф (титул) дворянский титул; «Граф» короткометражная немая кинокомедия Чарли Чаплина (The Count, 1916). От греч. γράφω «царапаю, черчу, пишу»: Граф… … Википедия
Граф (значения) — Граф: От древневерхненемецкого gravo, gravio «предводитель, вождь»: Граф (титул) дворянский титул; «Граф» короткометражная немая кинокомедия Чарли Чаплина (The Count, 1916). От греч. γράφω «царапаю, черчу, пишу»: Граф (в математике) объект,… … Википедия
граф — [титул] сущ., м., употр. часто Морфология: (нет) кого? графа, кому? графу, (вижу) кого? графа, кем? графом, о ком? о графе; мн. кто? графы, (нет) кого? графов, кому? графам, (вижу) кого? графов, кем? графами, о ком? о графах; сущ. графиня Граф … Толковый словарь Дмитриева
Граф Мар — (англ. Earl of Mar) один из старинных дворянских титулов в Шотландии. Об их землях см. Марр (Шотландия). Содержание 1 История 2 Мормеры Мара … Википедия
Граф Марч — или Граф Марки (англ. Earl of March) титул, который несколько раз создавался в Англии и Шотландии для представителей семей, владения которых располагались пограничных владениях (марках) между Англией с Уэльсом (Валлийская марка) и Англией с… … Википедия
Граф (титул)
Титул возник в IV веке в Римской империи и первоначально присваивался высшим сановникам (например, comes sacrarum largitionum «главный казначей»). Во Франкском государстве со второй половины VI века граф (гауграф) в своём округе-графстве/гау (нем. Gau — первоначально, сельская община у древних германцев, численностью ок. 100 человек) обладал судебной, административной и военной властью. По постановлению Карла II Лысого (877) должность и владения графа стали наследственными.
В период феодальной раздробленности — феодальный владетель графства, затем (с ликвидацией феодальной раздробленности) титул высшего дворянства. В качестве титула формально продолжает сохраняться в большинстве стран Европы с монархической формой правления.
В России титул введён Петром I (первым его получил в 1706 году Б. П. Шереметев). В конце XIX века учтено свыше 300 графских родов. Графский титул в советской России был ликвидирован Декретом ВЦИК и Совнаркома от 11 ноября 1917 года.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
О повести Гофмана см. Майорат (повесть)Майорат (от лат. major — старший) — порядок наследования имущества при обычном праве, согласно которому оно целиком переходит к старшему в роду или семье. Позже так стали называться и сами имения, унаследованные согласно такому праву. Этот порядок устанавливается в интересах сохранения целостности семьи или рода; когда минорат начинает способствовать их разложению.
Российское дворянство. За какие заслуги можно было стать графом?
Так уж сложилось исторически, что титул графа стал в России самым престижным, хотя по статусу и был ниже княжеского. До Петра I этот титул в стране не применялся. Впоследствии большинство российских графских родов носили титул, полученный их предками за особые заслуги от российских или иностранных монархов. Кроме того, было немало и бывших иностранных родов, перешедших в российское подданство, уже имея графский титул.
Создавая в стране единое служилое дворянское сословие, Петр искал возможности поднятия авторитета и значимости своих соратников, многие из которых выдвинулись из низов общества. В России к тому времени единственным широко применявшимся титулом был княжеский. Но присваивать его людям, не имеющим на него исторических прав, царь не рискнул, и так его отношения с родовитым и титулованным дворянством было трудно назвать хорошими.
Для начала Петр решил воспользоваться опытом других стран, где присвоение титулов по воле монарха и даже торговля титулами было делом обыденным. Уже в конце 1701 года император Священной Римской империи по просьбе Петра I возвел в графское достоинство видного российского дипломата генерал-фельдмаршала Ф. А. Головина, который имел в то время чин боярина. Графский титул сразу же возвысил Головина над остальным боярством.
Первый блин не оказался комом, и на следующий год таким же путем титул графа получил ближайший сподвижник царя А. Д. Меншиков. В 1706 году графом Священной Римской империи стал государственный канцлер Г. И. Головкин, начавший службу стольником при юном Петре еще в 1677 году.
В 1706 году Петр впервые сам произвел российского подданного в графы, этой высокой чести удостоился в награду за подавления бунта в Астрахани Б. П. Шереметев. Через три года титул российского графа, получил Г. И. Головкин, уже имевший иностранный графский титул.
Массовое «производство» российских графов началось в 1710 году, когда этот титул получили четыре человека, включая царского учителя Н. М. Зотова. Кстати, для Зотова титул оказался не распространяющимся на потомство: его детям и внукам пользоваться графским титулом было запрещено.
Впоследствии Петр возвел в графское достоинство своих соратников Я. В. Брюсса, А. М. Апраксина и П. А. Толстого. Последний через несколько лет стал первым человеком, которого лишили российского графского титула, произошло это после смерти Петра по инициативе Меншикова.
Любопытно, что и следующий пожалованный в российские графы (им стал при Екатерине I генерал-полицмейстер Санкт-Петербурга А. М. Девиер) тоже стараниями Меншикова был лишен титула.
При вдове Петра I графами стали еще пять человек: три брата Ливенвольде и двое родственников императрицы — Карл и Федор Скавронские.
Традицию возводить в графский титул безродных родственников затем продолжила Елизавета Петровна. При ней графами и графинями стали два брата и две сестры Гендриковых и еще несколько Скавронских. Не обошла императрица вниманием своего фаворита и, возможно, морганатического супруга Алексея Разумовского, а заодно и его брата Кирилла.
Порадев о близких людях, императрица стала присваивать высокий титул крупным военачальникам и государственным деятелям. При ней российскими графами стали Г. П. Чернышев, П. М. Бестужев-Рюмин, А. И. Румянцев, А. Б. Бутурлин, а также братья А. И. и П. И. Шуваловы.
Сведений о присвоении графских титулов Петром III я не нашел, но возможно, они были. Зато все графы, получившие титулы после государственного переворота от его супруги Екатерины II, хорошо известны. В первую очередь императрица возвела в графское достоинство участников заговора — пятерых братьев Орловых и двоих братьев Паниных.
Впоследствии Екатерина была скупа на присвоение высокого титула, но зато все, кто был его удостоен, оставили заметный след в истории России. При ней графами стали Г. А. Потемкин, А. В. Суворов (с присвоением приставки к фамилии «Рымницкий»), Н. И. Салтыков, М. Н. Кречетников, П. С. Потемкин и И. Е. Ферзен.
Из плеяды екатерининских графов, пожалуй, наименее известен генерал от инфантерии Ферзен. Это был бравый вояка, проведший всю жизнь в боях и походах, награжденный за доблесть тремя орденами святого Георгия (редчайший случай). После штурма Праги (пригорода Варшавы) в 1794 году Суворов доносил о Ферзене:
«Озараясь еще свежей славой, разбитием главнаго бунтовщика Костюшки и взятием его в плен, совокупил он новые лавры; при всей слабости здоровья, бодрствуя духом, превозмогал он и труды, и опасности, и как распоряжением по своей части, так и мужеством подтвердил известную о нем репутацию».
Именно за бои в Польше Иван Евстафьевич и стал российским графом.
Вступив на престол, Павел I стал активно увеличивать количество российских графов. В большинстве своем это были люди достойные, но заметный след в истории оставили только некоторые из них, в частности фельдмаршал М. Ф. Каменский, наказной атаман Войска Донского Ф. П. Денисов, да тогда еще генерал-лейтенант А. А. Аракчеев.
В период царствования Александра I многие пожалования высокого титула связаны с наполеоновскими войнами. Тогда российскими графами стали известные военачальники М. И. Голенищев-Кутузов, М. И. Платов, М. А. Милорадович, М. Б. Барклай-де-Толли, П. П. Коновницын, Ф.В. Остен-Сакен.
Все последующие императоры не скупились на графские титулы, а для награждения выбирали, как правило, людей достойных. Исторически сложилось, что в обществе графский титул всегда воспринимали как синоним знатности и высоких государственных заслуг. Этим он выгодно отличался от титула князя.
Стоит отметить, что в графское достоинство возводили и женщин, как правило, с возможностью передачи его детям. Не считая родственниц императриц, графинями стали статс-дамы Ливен и Баранова, а также вдовы видных государственных деятелей Протасова и Ростовцева.
В России было немало и иностранных графов, принятых в российское подданство. Только с присоединением части Польши в России добавилось около 70-ти графских родов, более 10-ти родов числились по Великому княжеству Финляндскому. В основном это были представители известных и богатых фамилий, уже давно имеющих графское достоинство или получивших его за конкретные заслуги.
Стоит отметить, что получение титула от иностранного монарха еще не означало, что человек может официально пользоваться им в России. Для этого было необходимо получить разрешение на пользование титулом от императора, а затем и на причисление к российскому титулованному дворянству. Если возникали сомнения в законности обладания иностранным графским титулом, то соизволение на его использование в России император мог и не дать.
Иногда российским подданным разрешали титулом пользоваться, но только в том государстве, где он был присвоен. Например, в конце XIX века родам Орловских и Талевичей император разрешил пользоваться графскими титулами, но только в пределах Итальянского королевства, монарх которого им эти титулы даровал.
Считается, что к началу ХХ века в России было около 300 графских родов. К этому времени часть графских родов пресеклась в мужском потомстве, а какое-то количество получило более высокий княжеский титул. При этом если графский титул сопровождался персональным титулованием, то он сохранялся и при получении княжеского титула.
Например, общий титул Суворова — светлейший князь Италийский, граф Рымникский, а Паскевича — светлейший князь Варшавский, граф Эриванский. И это только внутреннее российское титулование, так как Суворов имел еще и иностранные титулы — граф Священной Римской империи, гранд Сардинского королевства и принц королевской крови.
Графские титулы в России просуществовали до ноября 1917 года, когда новой властью был принят декрет «Об уничтожении сословий и гражданских чинов». С этого времени российские графские титулы употребляются только за границей в среде бывших эмигрантов и в некоторых странах, где сохранилась традиция титулования.
Просто о графах. Попытка популяризации
«Всякие звания (дворянина, купца, мещанина, крестьянина и пр., титулы — княжеские, графские и пр.) и наименование гражданских чинов (тайные, статские и проч. советники) уничтожаются. »
Как-то же я обходился без этого раньше.
Есть ли польза рядовому программисту или, скажем, обывателю от теории графов, или вещь эта сугубо сакральная, из надменных математических абстракций?
Вероятно, специфика “случайно распределенных графов” окажется маловостребованной в нашей с вами повседневности, но некоторое представление о теории графов может оказаться полезным в самых разнообразных ситуациях даже человеку не особенно к математике расположенному, – что же касается людей, занятых в такой области, как программирование, то изощренная изобретательность, как правило, сопутствует ежедневно выпадающим на их долю задачам, оттого представители этой профессии, в поисках новых идей и инструментов, случается, азартно загружают свой ум вещами, казалось бы не пригодными для полезного использования, однако, заказав пиццу за 10 тысяч биткоинов, они дарят хорошее настроение другим хорошим людям на многие годы, и таки оправдывают свою пассионарность.
Ну мы, допустим, себя причисляем к людям вполне серьезным и намерены вполне серьезно обратить себе на пользу малую толику знаний, которую мы трудно накапливаем и, с годами всё с более возрастающим трудом, удерживаем в своей голове. И роскошь небрежного забвения единожды усвоеной нами информации решительно отвергаем.
Граф может быть прекрасным средством визуализации посетившей вас идеи. Мы каждый день решаем какие-либо задачи, которые могут быть адекватно записаны языком графов, но часто не испытываем потребности в манипулировании зрительными образами. Иногда же именно зрительный образ оказывает то необходимое действие на нашу мыслительную концентрацию, которое приводит нас к светлой идее. – Часто оказывается полезным взглянуть на вещи с разных ракурсов.
Граф может оказаться выразителем сущности некоторой идеи и сократить вашу дорогу к конечной цели (если вы сейчас подумали о грустном, то я не имел это ввиду).
Часто бывает, что мы пользуемся не осознано, интуитивно, некоторыми приемами решения возникающих перед нами задач, которые – суть пользовательские шаблоны, подсказанные предыдущим опытом, а между тем, эти приемы, отлитые в идею, возведенные в парадигму, обращенные в концепцию могут стать мощнейшим инструментом, указывающим нам как направление, так и способ решения целого класса объединенных общим признаком проблем.
Теория графов к настоящему времени содержит достаточно много эффективных инструментов для решения столь же широкого круга проблем. Однако, средства и идеи, сегодня относящиеся к области дискретной математики, именуемой теорией графов, пребывают по сей момент в некотором эклектичном единстве как бы не без насильственного понуждения. Круг вопросов, решаемых теорией графов, и разнообразие привлекаемых для этого моделей и механизмов их решения столь обширны, что попытки популяризовать теорию графов в целом должны опираться на немалую дерзость. Академическое и глубокое изложение специфических нюансов теории графов не будет целью настоящей статьи. У нас есть намерение говорить лишь о том, чему мы нашли полезное (или относительно полезное) и нескучное применение.
И между прочим, «откуда есть пошло» теория графов?
… Это решение по своему характеру; по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике.
Из письма Леонарда Эйлера к своему другу Карлу Готлибу Элеру, 03 [14] апреля 1736 г. [1]
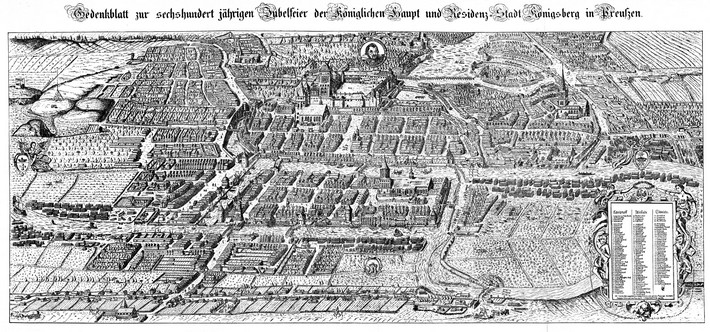
Рис. 1. Кёнигсберг на гравюре 17 века.
Считается, что теория графов начала оформляться как самостоятельная математическая дисциплина после показательного решения Эйлером «задачи о семи мостах«,– задачи чисто логистической,– применение теории графов к решению «задачи с четырьмя цветными кубиками«, на мой взгляд, требовало значительно большей изобретательности и большой искушенности в предмете, достигаемыми лишь постоянными упражнениями в практическом применении теории графов, хотя, к моменту решения последней из упомянутых задач от цитируемой переписки минуло более двух веков, и предмет новой дисциплины, лишь туманно виденной Эйлером, успел приобрести очертания вполне конкретные и накопить некоторый опыт практического применения усилиями выдающихся ученых, развивавших идеи Эйлера.
[Рис. 1 может дать некоторое представление о «задаче», упоминаемой в процитированной фразе.] Частью городской коммуникации и архитектурного ансамбля города Кёнигсберга в 1736 году являлись 7 мостов (эти старые мосты не сохранились) через реку Прегель. Трудно сказать, насколько широко была распространена загадка о том, можно ли пройти по всем семи мостам, не пройдя дважды ни по одному из них, и серьезно ли городские службы думали над утверждением такового маршрута для гостей города и горожан, но эта загадка сумела привлечь внимание Леонарда Эйлера, – правда, оставалась довольно длительное время единственным известным примером применения метода, предложенного великим математиком. Более ста лет работа Эйлера не вызывала особого интереса у ученого сообщества. Термин «граф» ввёл венгерский математик Дениш Кёниг только в 1936 году.
Некогда мне была предложена задача об острове, расположенном в городе Кёнигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно.
Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения не достаточны ни геометрия, ни алгебра, ни комбинаторное искусство.
Из письма Леонарда Эйлера к Джиованни Джакобо Маринони, 13 [24] марта 1736 г. [2]
(Судя по письмам Леонарда Эйлера, великий ученый не без удовольствия решал и другие головоломные задачи..)
Задача о семи мостах
Карлу Готлибу Элеру, 03 [14] апреля 1736
Я рассмотрел произвольно взятую фигуру разветвления реки, а также мосты а, b, с, d, e, f, как это указано на рисунке, и установил, что возможен переход, который я представляю следующим образом. Области, отделенные друг от друга водой, я называю буквами А, В, С, и когда предполагается переход через мосты из одной области в другую, [а именно] переход из А в В через мост или а или b, — наиболее удобно назвать [буквами] АВ, из которых первая буква А будет обозначать область, из которой переходят. Итак, АВСАСАВ будет определять переход, совершаемый через все мосты по одному разу; число этих букв должно быть на единицу больше, чем число мостов; это должно иметь место при любом возможном переходе описанным способом, в чем каждому легче убедиться самому, чем доказывать. Теперь я рассматриваю, сколько раз в ряде букв А, В, С, А, С, А, В должны встретиться буквы ABC, о чем нужно судить по числу мостов, ведущих в каждую из областей. Так, к области А ведут пять мостов: а, b, с, d, e, и сколько раз буква А встречается в середине того ряда, столько раз встречаются два из этих мостов, ибо с одной стороны нужно перейти в область А, с другой стороны — выйти оттуда. Если А встречается или в начале, или в конце того ряда, тогда единственный переход моста соответствует А. Отсюда следует, что, если число мостов, ведущих в область А, будет нечетным, тогда переход через все мосты не может совершиться иначе, чем таким образом, чтобы он или начинался в области А, или заканчивался в области А. А если число мостов, ведущих к А, будет четным, тогда переход может быть совершен и без этого условия, чтобы начинаться или заканчиваться в А, но если он начинается в А, то должен будет там же и закончиться. Отсюда вытекает, что в ряде АВСАСАВ любая буква, за исключением первой и последней, обозначает переход, ведущий через два моста в область, обозначенную этой буквой.
Следовательно, надо держаться следующего правила: если на каком-либо рисунке число мостов, ведущих в некоторую область, будет нечетным, тогда желаемый переход через все мосты одновременно не может быть осуществлен иначе, как если переход или начинается, или заканчивается в этой области. А если число мостов четное, отсюда не может возникнуть никакого затруднения, так как ни начало, ни конец перехода при этом не фиксируются. Отсюда следует такое общее правило: если будет больше чем две области, к которым ведет нечетное количество мостов, тогда желательный переход вообще не может быть совершен. Ибо представляется совершенно невозможным, чтобы переход и начинался, и заканчивался в какой-нибудь одной из этих областей. А если будут только две области такого рода (так как не могут быть даны одна область этого рода или нечетное число областей), тогда может быть совершен переход через все мосты, но с таким условием, чтобы начало перехода было в одной, а конец в другой из этих областей. Когда в предложенной фигуре А и В есть области, к которым ведет нечетное число мостов, а число мостов, ведущих к С, является четным, то я считаю, что переход или построение мостов может иметь место, если переход начинается или из А, или из В, а если же кто-нибудь пожелает начать переход из С, то он никогда не сможет достигнуть цели. В расположении кенигсбергских мостов я имею четыре области А, В, С, D, взаимно отделенные друг от друга водой, к каждой из которых ведет нечетное число мостов.
Таким образом, поскольку есть больше чем две области, к которым ведет нечетное число мостов, я утверждаю, что я доказал полную невозможность такого соединения мостов. Итак, с помощью очень легкого правила можно почти мгновенно определить для любой фигуры, допускается ли такого рода построение мостов, при котором переход будет происходить только через все мосты одновременно, или нет? Ибо возможным будет построение, если и не будет никакой области, или будут только две, к которым ведет нечетное число мостов; в таких случаях начало перехода выбирается произвольно, но там же должен быть и конец перехода. В последнем же случае начало перехода должно иметь место в одной из тех областей, а конец — в другой. Построение невозможно, если будет более чем две области, к которым поведет нечетное число мостов.
Рис. 2. Граф Кёнигсбергских мостов.
Рис. 3. Головоломка «Конверт».
Следовательно, ты можешь убедиться, славнейший муж, что это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека, ибо это решение подкрепляется одним только рассуждением и нет необходимости привлекать для нахождения этого решения какие-либо законы, свойственные математике. Итак, я не знаю, каким образом получается, что вопросы, имеющие совсем мало отношения к математике, скорее разрешаются математиками, чем другими [учеными]. Между тем ты, славнейший муж, определяешь место этого вопроса в геометрии положения, и что касается этой новой науки, то, признаюсь, мне неизвестно, какого рода относящиеся сюда задачи желательны были Лейбницу и Вольфу. Итак, я прошу тебя, если ты считаешь, что я способен нечто создать в этой новой науке, чтобы ты соблаговолил мне прислать несколько определенных, относящихся к ней задач, для того, чтобы я мог лучше уяснить себе, что именно представляется желательным. Между тем, поскольку мне известно, что Ты также можешь составить суждение о математических науках на основании одной только задачи, которую следует предложить и решить, начало чему по Твоей просьбе предложил преславный Кюн, я хотел бы, чтобы он представил нам такого рода задачи, которые он считает более трудными, [сделав это] как для прогресса науки, так и для упражнения наших сил.
Едва ли приведенные выше рассуждения Леонарда Эйлера вызвали у вас благоговейный трепет, какой, например, совершенно извинителен для человека, сколько-нибудь приобщенного к математике, восхищенно перебирающего следствия эффектной формулы Эйлера для комплексных чисел.
Следствие Формулы, связывающее пространства иррациональных и мнимых чисел:
Поскольку из Формулы Эйлера следует, что 
, нетрудно видеть, что
Впрочем, впечатлиться можно простым перечислением заслуг этого великого человека перед наукой…
Однако же, уж очень эта трёхсотлетней давности «задача о Кенигсбергских мостах» (Рис. 2) напоминает вам «конвертик», который в начальных классах вы успешно рисовали в «один проход» (Рис. 3), с каждым новым открытым вами способом нарисовать этот «конверт» умножая свое торжество над соревнующимися с вами в этом занятии одноклассниками.
Сколько сегодня найдете маршрутов? Полагаю, что внимательно читавшие выше письма Эйлера не ошибутся в выборе начальных точек для построения своих маршрутов (в первом классе у вас не было такой подсказки?), и предсказать, где их маршруты завершатся, тоже не составит труда. Заодно, достройте восьмой мост в «городе мыслителей» и наполните желанным смыслом пешие прогулки его жителей.
А мостов могло быть и больше.
В задачнике Генри Э.Дьюдени «520 головоломок» (я располагаю изданием 1975 года, Издательство «Мир», Москва [3] ) есть немало задач, которые могут быть решены прямо по инструкциям Эйлера. Взглянем на одну из таких задач, которой в указанном издании присвоен номер 408.
Эйлер вооружил нас надежным приемом, и мы решим задачу Дьюдени №408 запросто. Однако, скажем прямо, когда эта книга у меня завелась, я и представления не имел о рекомендациях Эйлера.
Зная путь, указанный нам великим математиком, мы способны, пожалуй, и на некоторые самостоятельные шаги. Как часто бывает, если часть задачи решили за нас, оставшуюся часть решить уже кажется проще. Зная, где мне сделать первый шаг, я, пожалуй, могу написать короткую инструкцию для подсчета или даже диспетчеризации возможных маршрутов.
Если вы решите повторить эти вычисления, не забудьте, что нечетный узел «С», с которого я начинаю движение, имеет степень 3. Этой же программой можно посчитать «конверт» и сравнить результат с маршрутами, найденными «вручную».
Итого, маршрутов насчитывается 67344 вариантов. Несколько многовато, но настоящая дружба должна быть способна вынести и такое количество визитов, осталось найти «настоящую» обувь, т.к. это испытание и для неё.
Пути и деревья
Графические схемы, конечно же, не исчерпываются замкнутыми маршрутами, и наш путь ведет нас к деревьям…
С 1978 года в мире, лежащем за пределами ваших компьютеров, то там, то сям, и никогда не здесь, происходят нешумные или даже почти конспиративные встречи незнакомых со мной (я так полагаю) людей, зовущиеся International Puzzle Party. Получить приглашение на это мероприятие можно только от члена этого закрытого клуба. Где и когда произойдет следующая встреча, никогда не известно за пределами клуба. Если верить лаконичному анонсу официального сайта IPP, то опаснее рукопожатий коллекционеров головоломок на самих «пати» ничего не происходит. Однако, постфактум тайного собрания, прочим смертным случается увидеть каталог диковинных головоломок, тщательно проинспектированных искушенным в головоломных задачах комитетом этого элитарного форума. Одна из таких головоломок, представленная на IPP 37, проходившем в августе 2017 года в Париже (вы тоже почувствовали влечение к коллекционированию головоломок?), была предложена участником «форума нешарнирных головоломок» (я несведущ в его международных перемещениях) в качестве разминки для мозгов охочим до такого досуга коллегам.
Мне эта головоломка показалась несколько напоминающей задачу Дьюдени, обремененную, однако, несколькими нюансами.
Разработчиком (создателем, творцом, демиургом) этого образца неординарной мысли, шедевра изощренной человеческой изобретательности отмечен Donghoon Pee – творец, видимо, скромный и незаслуженно малоизвестный здесь на Хабре,– последнюю несправедливость мы сейчас исправим, хотя, конечно, загубим интригу… Мне и самому жалко лишать читателей Хабра возможности самостоятельно поразмыслить над головоломкой 2&1 автора Donghoon Pee – могу лишь посоветовать тем, кто страстно желает решить головоломку самостоятельно, закрыть ладошками рисунки и часть относящегося к головоломке текста ниже.
У Donghoon Pee (Донгун Пи – наиболее вероятное прочтение, но, чтобы не рисковать, буду пользоваться латинским написанием) есть свой канал на youtube.com, страница в фейсбуке, проживает он в городе Сеуле и является профессиональным создателем (язык не поворачивается сказать «дизайнером», хотя сам он именно так зовет свой род занятий) головоломок. И его работы не раз удостаивались внимания клуба IPP. Будем надеяться, доходы этого безусловно достойного человека не понесут ущерба от этой публикации.
Небольшая модификация задачи может превратить её в задачу на плотную упаковку и т.п., но в узнаваемых пределах мы можем придерживаться модели, допускаемой теорией графов. Разумеется, с ростом серьезности поставленной задачи может возникнуть необходимость учета алгоритмической сложности и ограниченности рекурсивного механизма.
Задача с четырьмя цветными кубиками
Попробуем придать нашему обозрению видимость чуть большей академичности, для чего еще раз обратимся к «головоломке с четырьмя цветными кубиками».
Решая эту головоломку методом обычного перебора, мы прибегаем к методу обещающему нам 41472 иттераций. Изящнейшее же решение в графах потребует перебора комбинаций из четырех кубиков, описанных тремя парами цветов. – Разница ощутимая. Напомню легко алгоритмизируемую процедуру:
Имея инструкции для второго набора – т.е. для второй пары граней пирамиды, мы можем окончательно собрать комбинацию, являющуюся решением головоломки. Таким образом, выделив из мультиграфа (совокупности графов кубиков) два подграфа, указывающих на различные наборы цветов, – а для этого достаточно, чтобы одно и тоже ребро (поскольку именно ребро указывает на связь) не использовалось одновременно в каждом из графов,– мы получим легко читаемое решение головоломки: нам достаточно, например, согласно первой инструкции расположить кубики в соответствии «верх-низ» и привести их в соответствии со второй инструкцией, поворачивая вправо-влево. [Напомню, что «петля» так же является узлом 2-ой степени]. Из всех представленных на рисунке подграфов, только два образуют пару с несовпадающими ребрами. Это так называемое «единственное решение» «правильной» головоломки.
Не лишнее, вероятно, подробно рассмотреть пример развертки мультиграфа для красивой сборки, имеющей в 24-х положениях на каждой из своих сторон все 4-е цвета («неправильная» головоломка, на предыдущей публикации предыдущей публикации она представлена на Рис. 6): три подграфа (на левом рисунке, это три крайних левых подграфа) могут складываться в три пары с несовпадающими ребрами – сборка с «тремя решениями» по терминологии, распространенной в англоязычной среде.
Если мне в некотором, условно говоря, «потоке кубических сущностей» понадобится «выловить симметричные сборки», я постараюсь избежать банального перебора. Например, из кубиков, развертки которых приведены на Рис.2 той же публикации можно быстро сложить 16 наборов с «тремя решениями».
Граф указывает нам на внутреннюю связь, на уникальную природу некоторой изучаемой нами вещи. Воспользоваться замеченной особенностью вполне естественно, особенно, если модель обещает нам некоторое преимущество в сравнении с другими путями решения задачи.
Обратное моделирование
Можно ли от желаемой графической модели перейти к конкретной реализации чего бы то ни было? – Едва ли существует однозначный ответ, но в большинстве случаев я бы советовал не пытаться осуществить подобные переходы, если только искомая вами модель не ограничивается полностью описываемыми в рамках графического прототипа особенностями. Описывая объект из реального мира, вы пренебрегаете частью его свойств перед одной сущностной особенностью, в угоду выбранной вами модели.
Например, у 1073-х уникальных наборов кубиков по четыре число отвечающих этим наборам уникальных графов существенно меньше: если принимать во внимание в топологии графа лишь сочетание его ребер и узлов, опуская нумерацию ребер, то можно выделить лишь 204 уникальных графов для возможных головоломок из четырех цветных кубиков.
Графы решений,— те два пути обхода узлов, которые необходимо выделить из мультиграфа,– будут подобны, хотя сам исходный мультиграф может делиться различным образом, т.к. нумерация граней все-таки вносит особенности в общую топологию графа. Графическая модель, которую мы используем для нахождения решения головоломки, подобной Instant Insanity, характеризует наборы кубиков только с точки зрения оптимизации поиска решения этой головоломки. Эта модель построена на основе анализа топологической структуры набора кубиков для решения только одной узкой задачи – задачи взаимного расположения кубиков. Отдельный мультиграф, как и граф отдельного кубика, не указывает на уникальность объекта, да и не должен – мы же сами искали нечто общее в явлении, а не в объекте. Портретный образ не предстает из лаконичной характеристики «характер – твердый, нордический».
Рис. 4. 204 графа «головоломки с четырьмя цветными кубиками».
Изоморфизм
Есть различные способы выявления изоморфизма графов, но описание любого из них, по моему мнению, избыточно для и без того затянувшейся статьи. Однако, без иллюстрации к «чуду превращения» некоторая часть читателей может счесть себя разочарованной, а я предпочитаю, чтобы она нашла себе для этого другие причины.
Возьмем развертку головоломки Instant Insanity на сайте Роберта Штегманна (R.Stegmann – он то, наверное, «рукопожатый» всем клубом IPP!) — я буду придерживаться следующего порядка обхода граней кубика: нижняя грань→лицевая→верхняя→задняя→левая→правая.
Самая распространенная из разверток с отмеченного сайта (автором собрано и несколько клонов, но мы ориентируемся на «классический» вариант головоломки) будет в выбранном порядке обхода граней записана следующим образом: RWGGWB, RBBWGG, RGWWRB, GWRBRR.
Надеюсь, что никому не удалось забыть, что при записи графа мы принимаем во внимание лишь пары цветов противоположных граней, и поэтому строчная запись графической конфигурации выбранных кубиков выглядит не иначе, чем: RG|WG|WB, RB|BW|GG, RW|GW|RB, GR|WB|RR. Как видим, мультиграф на первом рисунке полностью соответствует этому набору (ну лишь за исключением, что у меня желтый цвет вместо классического белого).
Возможно, не одному мне удобнее работать с цифрами, поэтому обозначим цифрами цвета (и исключим тем самым некоторое замеченное выше несогласие в цветах), а заодно запишем эту комбинацию кубиков сразу в положении решения (благо, что два подграфа, указывающие нам путь, у нас перед глазами):
Вместо заключения
Очень надеюсь, что чтение не было скучным. Возможно, кому-то оказалось отчасти полезным. И практически уверен, что количество нарисованных конвертиков к завтрашнему дню несколько возрастет, и кто-то наконец найдет в себе силы и мотивацию отвлечь наследника от его гаджета какой-нибудь занимательной и умной задачей. Эйлер вот не пренебрегал…
1.↑ Леонард Эйлер. Письма к ученым, Издательство АН СССР, 1963, стр.339
2.↑ Леонард Эйлер. Письма к ученым, Издательство АН СССР, 1963, стр.153
3.↑ Генри Э. Дьюдени. 520 головоломок. Составитель и редактор американского издания М. Гарднер, Издательство МИР, Москва, 1975
Развертки кубов переставлены в порядке 1342. Соответствующий разверткам мультиграф размещен третьим среди графов задачи.
Правильный ответ: «третий».