Кто такой клод шеннон и чем он знаменит информатика
Кто такой Клод Шеннон и чем он знаменит?

Клод Элвуд Шеннон — известный американский инженер и математик. Его работы совмещают связь математических идей с анализом весьма сложного процесса их технической реализации. Клод Шеннон знаменит в первую очередь благодаря разработке теории информации, которая служит основой современных высокотехнологических систем связи. Шеннон внес огромный вклад в ряд наук, которые входят в понятие «кибернетики» — он создал теорию вероятности схем, теорию автоматов и систем управления.
Клод Шеннон — становление инженерного гения
Клод Шеннон родился в 1916 году в городе Гейлорд, штат Мичиган, США. Технические конструкции, как и общность математических процессов, интересовали его с ранних лет. Все свое свободное время он решал математические задачи и возился с радиоконструкторами и детекторными приемниками.
Неудивительно, что будучи студентом Мичиганского университета, Шеннон одновременно специализировался в математике и электротехнике. Благодаря высокой образованности и разнообразию интересов, первый огромный успех к Шеннону пришел уже во время учебы в аспирантуре Массачусетского технологического университета. Тогда ему удалось доказать, что работу электрических схем реле и переключателей можно представить посредством алгебры. За это величайшее открытие Клод Шеннон был удостоен Нобелевской премии. Причину своего ошеломляющего успеха он объяснил достаточно скромно: «Просто до меня никто не изучал математику и электротехнику одновременно.»
Шеннон и криптография
В 1941 году Шеннон стал сотрудником Bell Laboratories, где его основной задачей была разработка сложных криптографических систем. Эта работа позволила ему создать методы кодирования с возможностью коррекции ошибок.

Клод Шеннон стал первым, кто сформулировал теоретические основы криптографии и раскрыл суть многих понятий, без которых криптография, как наука не существовала бы.
Основоположник информатики
В какой-то момент своей деятельности, Клод Шеннон поставил перед собой задачу улучшить передачу информации по телефонным и телеграфным каналам, которые находятся под воздействием электрических шумов. Тогда ученый выяснил, что наилучшим решением данной проблемы станет более эффективная «упаковка» информации. Однако прежде, чем приступить к исследованиям ему пришлось ответить на вопрос, что же такое информация и чем измерить ее количество. В 1948 году в статье «Математическая теория связи» он описал определение количества информации через энтропию, величину, которая известна в термодинамике как мера разупорядоченности системы, а наименьшую единицу информации назвал «битом».
Позже, основываясь на своих определениях количества информации, Шеннону удалось доказать гениальную теорему о пропускной способности зашумленных каналов связи. В годы ее разработки, теорема не нашла практического применения, зато в современном мире высокоскоростных микросхем она находит применение везде, где хранится, обрабатывается или передается информация.
Почти современник
Вклад Клода Шеннона в науку и его результаты трудно переоценить, ведь без его открытий стало бы невозможным существование компьютерной техники, Интернета и всего цифрового пространства. Кроме теорий, которые положили начало развития информационных технологий, гениальный инженер и математик так же сделал вклад в развитие многих других областей. Он одним из первых доказал то, что машины не только способны выполнять интеллектуальную работу, но и обучаться. В 1950 году, он изобрел механическую радиоуправляемую мышку, которая благодаря сложной электронной схеме могла найти дорогу в лабораторию самостоятельно. Также он стал автором устройства, которое было способно складывать кубик Рубика, а так же изобрел Гекс – электронное устройство для настольных игр, которое всегда побеждало соперников.
Гениальный ученый и изобретатель умер на 84 году жизни в 2001 году от болезни Альцгеймера в массачусетском доме престарелых.
Шеннон, Клод Элвуд
В 1948 году опубликовал фундаментальную работу A Mathematical Theory of Communication, в которой сформулированы основы теории информации. Большую ценность представляет другая работа — Communication Theory of Secrecy Systems ( 1949 ), в которой сформулированы математические основы криптографии.
C 1956 — член Национальной академии наук США и Американской академии искусств и наук.
Содержание
Книги на русском языке [ ]
Шеннон К. Работы по теории информации и кибернетике. – М.: ИЛ, 1963
См. также [ ]
Теоремы Шеннона [ ]
В теории информации, по традиции, утверждения типа «для любого кода имеет место некоторое свойство» называются обратными теоремами, а утверждения типа «Сущеcтвует код с заданным свойством» — прямыми теоремами. [1]
Литература [ ]
Ссылки [ ]
ar:كلود شانون bn:ক্লদ শ্যানন bs:Claude E. Shannon ca:Claude Elwood Shannon cs:Claude Shannon de:Claude Elwood Shannon en:Claude Shannon eo:Claude Shannon es:Claude Elwood Shannon eu:Claude Shannon fa:کلود شانون fi:Claude Shannon fr:Claude Shannon he:קלוד שאנון ht:Claude Shannon hu:Claude Shannon is:Claude Shannon it:Claude Shannon ja:クロード・シャノン ko:클로드 섀넌 ml:ക്ലോഡ് ഷാനണ് nl:Claude Shannon no:Claude Elwood Shannon pl:Claude E. Shannon pt:Claude Elwood Shannon ro:Claude Shannon sk:Claude Elwood Shannon sl:Claude Elwood Shannon sr:Klod Elvud Šenon sv:Claude Shannon th:คล็อด แชนนอน tr:Claude Elwood Shannon uk:Шеннон Клод zh:克劳德·香农
Клод Шеннон: как гений решает проблемы
Клоду Шеннону потребовалось около десяти лет, чтобы полностью сформулировать свою эпохальную теорию информации.
Сначала, в аспирантуре, он вынашивал идею подвести общую базу под множество информационных технологий своего времени (таких как телефон, радио, телевидение).
Однако только в 1948 году он опубликовал Математическую Теорию Связи.
Правда, это был не единственный его крупный вклад в науку. Еще будучи студентом MIT (Массачусетский технологический институт), в свои скромные 21, он опубликовал работу, которую многие считают, пожалуй, наиболее важной магистерской диссертацией века.
Для обычного человека значение ее невелико. Нельзя сказать, что имя Шеннона у всех на устах. Но, если бы не работа Шеннона, то никакого компьютера в современном понимании могло не появиться. Шеннон оказал колоссальное влияние не только на информатику, но и на физику, и на инженерию.
Мы запросто бросаемся словом «гений», но лишь немногие люди на свете по праву заслужили именоваться так, и Клод Шеннон — один из них. Он мыслил иначе, мыслил играючи.
Одной из малозаметных основ его гениальности, проявлявшейся таким образом, был его подход к решению задач. Он не просто формулировал вопрос, а затем искал ответ на него, но методологически разрабатывал процесс, помогавший рассмотреть суть за очевидным.
Его задачи отличались от большинства из тех, с которыми нам, вероятно, доводилось иметь дело, но его шаблоны и принципы рассуждения до некоторой степени поддавались генерализации и, освоив такое обобщение, мы и сами можем научиться мыслить проницательнее.
Любая задача имеет очертания и форму. Для решения задач первым делом нужно научиться их понимать.
Формулируем суть, затем дополняем детали
Любому из нас понятно, как важно получать ответы, но многие в самом деле пренебрегают тем, как важно сформулировать вопрос именно таким образом, чтобы ответ на него действительно нам достался.
Мы быстро перескакиваем от нюанса к нюансу, надеясь, что рано или поздно они сложатся воедино, а не бросаем все силы на развитие интуиции в той дисциплине, которой занимаемся.
Именно здесь Шеннон действовал в точности наоборот. На самом деле, как отмечают его биографы в книге A Mind at Play, он настолько этим увлекался, что некоторые математики-современники считали, будто он недостаточно дотошно подходил к выстраиванию согласованной картины. Естественно, их интересовали детали.
Однако, по мысли Шеннона, увидеть суть исследуемой проблемы и, соответственно, путь к ответу, можно лишь после того, как отсечешь от нее несущественные детали.
На самом деле, зачастую, подходя к такой сути, проблема уже может не ощущаться — и это подсказывает, как важно составить общее впечатление, прежде чем переходить к деталям. В противном случае можно направиться по ложному пути.
Детали важны и полезны. На самом деле, многие детали несравнимо важнее и полезнее, чем кажутся на первый взгляд. Однако ничуть не меньше и бесполезных деталей.
Если не найти суть проблемы, то начинаешь совершенно не с тех деталей, из-за чего добавляются все новые и новые неверные детали, и так пока вы не увязнете.
Начиная отсекать несущественное, вы дисциплинируете себя, и учитесь видеть суть за дымкой несущественного. Именно тогда вы находите те основания, которые искали.
Обнаружить истинные очертания проблемы почти столь же важно, как и последующий ответ.

Источник
В докладе, прочитанном в компании Bell Labs в 1952 году перед современниками, Шеннон подробно остановился на том, как тренирует собственный разум, развивая креативный подход к своим долгосрочным задачам.
Он не только упрощал их, доискиваясь сути, но и предлагал кое-что еще — на первый взгляд, казалось бы, несущественное, но критически важное для нестандартного мышления.
Зачастую, подолгу размышляя над проблемой, мы начинаем мыслить ограниченно и строго придерживаемся единственной траектории. Логическое рассуждение начинается с некоторой точки, далее делаются обоснованные выводы и, если рассуждать правильно, то логика всегда приводит нас к одному и тому же ответу.
Креативное мышление устроено немного иначе. Здесь также улавливаются взаимосвязи, однако, такие суждения не столько логические, сколько интуитивные, позволяющие нам развить новые паттерны мышления.
Один из излюбленных приемов Шеннона заключался в перестраивании задачи и сравнении ее по максимально разным параметрам. Таким образом, он мог ее утрировать, преуменьшать, формулировать иными словами, менять угол рассмотрения и инвертировать.
Суть такого упражнения — попросту добиться более целостного представления о происходящем.
Наш мозг легко зацикливается на тех или иных мыслях, и лучший способ вырваться из такой петли — изменить систему отсчета. Мы не меняем интуитивного представления о проблеме и не отказываемся от выявленной сути, меняем лишь подачу материала.
Например, можно спросить: каким образом лучше всего это решить? Но возможен и такой вопрос: а каков наихудший способ решения? В ответе на оба этих вопроса — знание, и мы должны проанализировать оба варианта.
Проблема может иметь не только разную форму, но и множество очертаний. Разные очертания заключают в себе разные истины.
Умножаем сущность всех вводных данных
Притом, что важно уделять внимание качеству идей, не менее важно, пожалуй, думать о количестве. Нас волнуют не только итоговые цифры, но и то, как мы приходим к этим цифрам.
Для решения задачи необходима хорошая идея. В свою очередь, найти хорошую идею обычно удается лишь после того, как отбросишь множество плохих. Так или иначе, выдавать на-гора все, что приходит в голову — не вариант. Дело не только в этом.
В годы Второй мировой войны Шеннон познакомился с Аланом Тьюрингом, еще одним первопроходцем информатики. Пока Тьюринг был в США, они встречались почти каждый день. Долгие годы они не теряли контакта, оба уважали идеи друг друга и наслаждались компанией друг друга.
Шеннон, рассуждая о том, что же на его взгляд составляет сущность гения, воспользовался аналогией, подсказанной Тьюрингом, и на ее основе вывел одно тонкое наблюдение. По словам самого Шеннона:
Есть такие люди, которым закинешь идею в голову — и на выходе получишь половину новой идеи. Некоторые способны на большее: они выдают по две новые идеи на каждую полученную.
Из скромности он отказывался причислять себя ко второй категории, относя к ней, например, Ньютона. Однако, если присмотреться к ситуации, то понятно, что у нас в игре. Речь не только о количестве.
Любые исходные данные в основе своей несут истину, которая не заметна при поверхностном рассмотрении. Истина — это основа для множества разнообразных решений множества разных задач.
Полагаю, Шеннон догадался, что генерация хороших идей требует умножать сущность каждых данных. Плохие идеи могут появляться, если вы неправильно уловили суть, но, чем лучше вы ее очерчиваете, тем плодотворнее будет ваш поиск озарений.
Удвоение отдачи от ваших идей — это первый шаг, но по-настоящему важно схватывать их суть.
Все, что нужно знать
Значительная часть жизни — будь то в работе, в отношениях с людьми, в заботе о себе — сводится к выявлению проблемы и умению к ней подступиться так, чтобы затем она миновала.
Возможно, Клод Шеннон был гением-одиночкой, обладал уникальным разумом, но его метод вполне доступен для любого из нас. Сила его была именно в этом методе и умении его применять.
Умение хорошо решать задачи — плод как критического, так и творческого мышления. Наилучший способ их скомбинировать — вооружиться методом, который позволит максимально выгодно использовать и то, и другое.
Паттерны мышления формируют наш разум. Цель — выработать для этого правильные паттерны.
Перевод статьи выполнен в Alconost.
Alconost занимается локализацией игр, приложений и сайтов на 70 языков. Переводчики-носители языка, лингвистическое тестирование, облачная платформа с API, непрерывная локализация, менеджеры проектов 24/7, любые форматы строковых ресурсов.
Мы также делаем рекламные и обучающие видеоролики — для сайтов, продающие, имиджевые, рекламные, обучающие, тизеры, эксплейнеры, трейлеры для Google Play и App Store.
Кто такой клод шеннон и чем он знаменит информатика
Источник шифрования устанавливает предел максимального сжатия данных и числовое значение энтропии Шеннона.
Клод Шэннон родился 30 апреля 1916 года в городе Петоцки, штат Мичиган, США. Первые шестнадцать лет своей жизни Клод провел в Гэйлорде, Мичиган, где в 1932 году он закончил общеобразовательную среднюю школу Гэйлорда. В юности он работал курьером службы Western Union. Отец его был адвокатом и в течение некоторого времени судьей. Его мать была преподавателем иностранных языков и впоследствии стала директором Гэйлордской средней школы. Молодой Клод увлекался конструированием механических и автоматических устройств. Он собирал модели самолетов и радиотехнические цепи, создал радиоуправляемую лодку и телеграфную систему между домом друга и своим домом. Временами ему приходилось исправлять радиостанции для местного универмага. Томас Эдисон был его дальним родственником.
По совету Буша Шзннон решил работать над докторской диссертацией по математике в MIT. Идея его будущей работы родилась у него летом 1939 года, когда он работал в лаборатории в Колд-Спринг-Харбор (штат Нью-Йорк). Буш был назначен президентом Института Карнеги в Вашингтоне и предложил Шэннону принять участие в работе, которую делала Барбара Беркс по генетике. Именно генетика, по мнению Буша, могла послужить предметом приложения усилий Шэннона. Докторская диссертация Шеннона, получившая название «Алгебра для теоретической генетики», была завершена весной 1940 года. Шэннон получает докторскую степень по математике и степень магистра по электротехнике.
В период с 1941 по 1956 гг. Шэннон преподает в Мичиганском университете и работает в компании Белл (Bell Labs). В лаборатории Белл Шэннон, исследуя переключающие цепи, обнаруживает новый метод их организации, который позволяет уменьшить количество контактов реле, необходимых для реализации сложных логических функций. Он опубликовал доклад, названный «Организация двухполюсных переключающих цепей». Шеннон занимался проблемами создания схем переключения, развил метод, впервые упоминавшийся фон Нейманом и позволяющий создавать схемы, которые были надежнее, чем реле, из которых они были составлены. В конце 1940 года Шэннон получил Национальную научно-исследовательскую премию. Весной 1941 года он вернулся в компанию Белл. С началом Второй мировой войны Т. Фрай возглавил работу над программой для систем управления огнем для противовоздушной обороны. Шэннон присоединился к группе Фрая и работал над устройствами, засекавшими самолеты противника и нацеливавшими зенитные установки, также он разрабатывал криптографические системы, в том числе и правительственную связь, которая обеспечивала переговоры Черчилля и Рузвельтачерез океан. Как говорил сам Шеннон, работа в области криптографии подтолкнула его к созданию теории информации.
С 1950 по 1956 Шэннон занимался созданием логических машин, таким образом, продолжая начинания фон Неймана и Тьюринга. Он создал машину, которая могла играть в шахматы, задолго до создания Deep Blue. В 1952 Шеннон создал обучаемую машину поиска выхода из лабиринта.
Шэннон уходит на пенсию в возрасте пятидесяти лет, в 1966 году, но он продолжает консультировать компанию Белл (Bell Labs). В 1985 году Клод Шэннон со своей супругой Бетти посещает Международный симпозиум по теории информации в Брайтоне. Шеннон довольно долго не посещал международные конференции, и сначала его даже не узнали. На банкете Клод Шэннон дал короткую речь, пожонглировал всего тремя мячиками, а затем раздал сотни и сотни автографов изумленным его присутствием ученым и инженерам, отстоявшим длиннейшую очередь, испытывая трепетные чувства по отношению к великому ученому, сравнивая его с сэром Исааком Ньютоном.
Он был разработчиком первой промышленной игрушки на радиоуправлении, которая выпускалась в 50-е годы в Японии (фото). Также он разработал устройство, которое могло складывать кубик Рубика (фото), мини компьютер для настольной игры Гекс, который всегда побеждал соперника (фото), механическую мышку, которая могла находить выход из лабиринта (фото). Также он реализовал идею шуточной машины «Ultimate Machine» (фото).
Клод Шэннон ушел из жизни 24 февраля 2001 года.
Теория связи в секретных системах
Работа Шэннона «Теория связи в секретных системах» (1945) с грифом «секретно», которую рассекретили и опубликовали только лишь в 1949 году, послужила началом обширных исследований в теории кодирования и передачи информации, и, по всеобщему мнению, придала криптографии статус науки. Именно Клод Шэннон впервые начал изучать криптографию, применяя научный подход. В этой статье Шэннон определил основополагающие понятия теории криптографии, без которых криптография уже немыслима. Важной заслугой Шэннона является исследования абсолютно стойких систем и доказательство их существования, а также существование криптостойких шифров, и требуемые для этого условия. Шэннон также сформулировал основные требования, предъявляемые к надежным шифрам. Он ввёл ставшие уже привычными понятия рассеивания и перемешивания, а также методы создания криптостойких систем шифрования на основе простых операций. Данная статья является отправным пунктом изучения науки криптографии.
Статья «Математическая теория связи»

Решение проблемы избыточности подлежащего передаче сообщения позволяет максимально эффективно использовать канал связи. К примеру, современные повсеместно используемые методы снижения избыточности в системах телевизионного вещания на сегодняшний день позволяют передавать до шести цифровых программ коммерческого телевидения, в полосе частот, которую занимает обычный сигнал аналогового телевидения.
Решение проблемы передачи сообщения по каналам связи с шумами при заданном соотношении мощности полезного сигнала к мощности сигнала помехи в месте приема, позволяет передавать по каналу связи сообщения со сколь угодно малой вероятностью ошибочной передачи сообщения. Также, это отношение определяет пропускную способность канала. Это обеспечивается применением кодов, устойчивых к помехам, при этом скорость передачи сообщений по данному каналу должна быть ниже его пропускной способности.
В своих работах Шэннон доказал принципиальную возможность решения обозначенных проблем, это явилось в конце 40-х годов настоящей сенсацией в научных кругах. Данная работа, как и работы, в которых исследовалась потенциальная помехоустойчивость, дали начало огромному числу исследований, продолжающихся и по сей день, уже более полувека. Ученые из СССР и США (СССР — Пинскер (англ.)русск., Хинчин, Добрушин, Колмогоров; США —Галлагер (англ.)русск., Вольфовиц (англ.)русск., Файнстейн) дали строгую трактовку изложенной Шенноном теории.
На сегодняшний день все системы цифровой связи проектируются на основе фундаментальных принципов и законов передачи информации, разработанных Шэнноном. В соответствии с теорией информации, вначале из сообщения устраняется избыточность, затем информация кодируется при помощи кодов, устойчивых к помехам, и лишь потом сообщение передается по каналу потребителю. Именно благодаря теории информации была значительно сокращена избыточность телевизионных, речевых и факсимильных сообщений.
Большое количество исследований было посвящено созданию кодов, устойчивых к помехам, и простых методов декодирования сообщений. Исследования, проведенные за последние пятьдесят лет, легли в основу созданной Рекомендации МСЭ по применению помехоустойчивого кодирования и методов кодирования источников информации в современных цифровых системах.
Теорема о пропускной способности канала.
Любой канал с шумом характеризуется максимальной скоростью передачи информации, этот предел назван в честь Шеннона. При передаче информации со скоростями, превышающими этот предел, происходят неизбежные искажения данных, но снизу к этому пределу можно приближаться с необходимой точностью, обеспечивая сколь угодно малую вероятность ошибки передачи информации в зашумлённом канале
Кто такой Клод Шеннон и чем он знаменит
Клод Элвуд Шеннон – ведущий американский учёный в сфере математики, инженерии, криптоаналитики.
Он приобрёл мировую известность, благодаря своим открытиям в области информационных технологий и изобретению «бит» (1948 г.), как самой маленькой информационной единицы. Его считают основоположником информационной теории, основные положения которой до сих пор актуальны в разделе высокотехнологичной связи и современных коммуникаций.
Шенноном также было впервые введено понятие «энтропия», что говорит о неопределённой мере передаваемой информации.
Этот учёный первым применил научный подход для информационной идей и законов криптографии, обосновав свои мысли в работах о математической теории связи, а также о теории связи в секретных системах.
Большой вклад внёс он и в развитие кибернетики, обосновав такие ключевые моменты, как вероятность схемы, игровую научную концепцию, а также мысли о создании автоматов и управленческой системы.
Детские и юношеские годы
Клод Шеннон появился на свет в американском Петоски, что в штате Мичиган. Это радостное событие случилось 30.04.1916-го.
Отец будущего учёного занимался бизнесом в сфере адвокатуры, а затем был назначен судьёй. Мать – преподавала иняз и со временем получила должность директора школы в Гэйлорде.
Математические наклонности были присущи Шеннону-старшему. Ключевую роль в формировании склонности к научной деятельности у внука сыграл дедушка – фермер и изобретатель.
В его арсенале создание стиральной машинки и некоторых видов прикладной сельхозтехники. Примечательно, что Эдисон имеет родственные связи с этой семьёй.
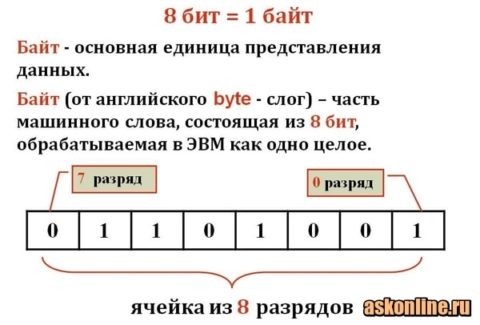
Фото: значение слова “байт”
В 16-летнем возрасте Клод закончил среднюю школу, где преподавала его мать. Успел поработать курьером в Western Union, занимался конструированием различных устройств.
Его интересовало моделирование самолётов и радиотехники, ремонт небольших радиостанций. Он своими руками сделал лодку с радиоуправлением, телеграф для связи с другом.
Как уверяет сам Клод, его абсолютно не интересовали только политика и вера в Бога.
Студенческие годы
Университет Мичигана распахнул перед Шенноном свои двери в 1932 году. Учёба здесь открыла для него труды Дж. Буля. Диплом бакалавра по математике и электротехнике Клод получил в 1936 г.
Его первым местом работы стала должность ассистента-исследователя в технологическом университете Массачусетcа. Научную деятельность Клод вёл в качестве оператора механического компьютерного устройства, созданного его учителем В. Бушем.
Глубоко вникнув в концептуальные научные разработки Буля, Шеннон понял возможность их практического применения. Защитив магистерскую диссертацию в 1937 г., которую курировал Фрэнк Л. Хичкок, он перешёл в известную Bell Telephone Laboratories, где выпустил материал по символическому анализу в схемах переключения и с задействованием реле.
Он был размещён на страницах специального журнала институтом инженеров-электриков в США (1938 г.).
Основные положения статьи раскрыли усовершенствование маршрутного посыла телефонного вызова, благодаря замене реле электромеханического типа на переключающую схему. Молодой учёный обосновал концепцию о возможности решения применением схем всех задач Булевой алгебры.
Эта работа Шеннона получила Нобелевскую премию в области электрической инженерии (1940 г.) и стала основой для создания логических цифровых схем в электрических цепях. Этот магистерский труд стал настоящим научным прорывом ХХ века, положив начало созданию электронной вычислительной техники современного поколения.
Буш рекомендовал Шеннону заняться диссертацией на получение степени доктора математических наук. Серьёзное внимание им было уделено математическим исследованиям в тесной связи с генетическими законами наследственности известного Менделя. Но эта работа так и не получила должного признания и впервые была опубликована только в 1993 г.
Немало сил учёным было отдано построению математического фундамента для различных дисциплин, особенно информационных технологий. Этому способствовало его общение с видным математиком Г. Вейлем, а также Дж. Фон Нейманом, Энштейном, Гёделем.
Военный период
С весны 1941 г. до 1956 г. Клод Шеннон работает на оборону США, разрабатывая управление огнём и обнаружение врага при ведении противовоздушной обороны. Он создал устойчивую межправительственную связь президента США с английским премьером.
Национальной премии в области научных исследований он был удостоен за свой доклад об организации двухполюсных переключающих цепей (1942 г.).
Учёный заинтересовался идеями англичанина Тьюринга по шифрованию речи (1943 г.), и уже в 1945-м выпустил работу об усреднении данных и прогнозировании для систем управления огнём. Его соавторами стали Ральф Б. Блэкмен и Х. Боде. Смоделировав специальную систему, обрабатывающую информацию и спецсигналы, они положили начало информационному веку.
Секретный меморандум К. Шеннона в области математической теории криптографии (1945 г.) доказал, что криптография и теория связи – неразделимы.
Послевоенный период
Это время ознаменовано его меморандумом о теории связи с математической точки зрения (1948 г.) в части кодировки передаваемых текстов.
Дальнейшая работа Шеннона вплотную связана с информационной теорией в области разработки игр, в частности колеса рулетки, машины, читающей мысли, а также машины по сбору кубика Рубика.
Учёный воплотил идею, позволяющую сжать информацию, которая позволяет избежать её потерю при распаковке.
Учёный создал школу, где периодически вёл семинары, где учил студентов находить новые подходы к решению тех или иных задач.
Известны его научные исследования в области финансовой математики. Среди них, электрическая цепь денежного течения в американских пенсионных фондах и обоснование выбора портфеля инвестиций при распределении денежных активов.
Многие сравнивают популярность Клода Шеннона с Исааком Ньютоном.
После 1978 г., на пенсии он занялся теорией жонглирования и сконструировал специальную машину.
Сборник своих статей Клод Шеннон выпустил в 1993 году, куда вошли 127 его научных работ.
Завершающий жизненный этап
Последние годы он провёл в Массачусетском доме-интернате из-за болезни Альцгеймера. Здесь, по заверению его жены Мэри Элизабет, Клод участвовал в исследованиях по изучению способов её лечения.
У Шеннона остались единственная жена, брак с которой продлился с марта 1949 г. У них родились трое детей Роберт, Андрю, Маргарита.