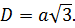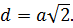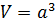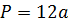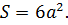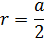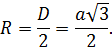Куб что это такое в математике
Куб (алгебра)
Кубом числа называется результат умножения числа на само себя трижды (возведения числа в степень 3). Куб величины 

|
|
Сумма чисел в k-ой (k=1,2,…) выделенной области первой таблицы:
А сумма чисел в k-ой (k=1,2,…) выделенной области второй таблицы, представляющих собой арифметическую прогрессию:
Суммируя по всем выделенным областям первой таблицы, получаем такое же число, как и суммируя по всем выделенным областям второй таблицы:
Геометрический смысл
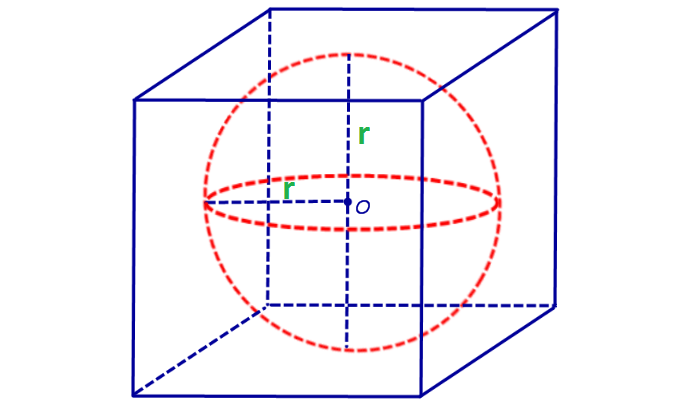
Куб числа равен объёму куба с длиной ребра, равной этому числу.
Некоторые свойства
См. также
Примечания
Полезное
Смотреть что такое «Куб (алгебра)» в других словарях:
Квадрат (алгебра) — У этого термина существуют и другие значения, см. Квадрат (значения). y=x², при целых значениях x на отрезке от 1 до 25 Квадратом числа называется результат умножения числа на себя (воз … Википедия
Список статей по математической логике — Это служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не ус … Википедия
Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ … Википедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
Параллелепипед — (от греч. παράλλος параллельный и греч. επιπεδον плоскость) призма, основанием которо … Википедия
МНОГОГРАННИК — часть пространства, ограниченная совокупностью конечного числа плоских многоугольников (см. ГЕОМЕТРИЯ), соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого… … Энциклопедия Кольера
8 (число) — 8 восемь 5 · 6 · 7 · 8 · 9 · 10 · 11 Факторизация: 2×2×2 Римская запись: VIII Двоичное: 1000 Восьмеричное: 10 Шестнадцатеричное: 8 … Википедия
Тетраэдр — (греч. τετραεδρον четырёхгранник) простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Содержание 1 Связанные определения … Википедия
Карта Карно — Рис. 1 Пример Куба Карно Куб Карно графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного… … Википедия
Восемь — 8 восемь 5 · 6 · 7 · 8 · 9 · 10 · 11 Факторизация: 2×2×2 Римская запись: VIII Двоичное: 1000 Восьмеричное: 10 Шестнадцатеричное … Википедия
Куб что это такое в математике
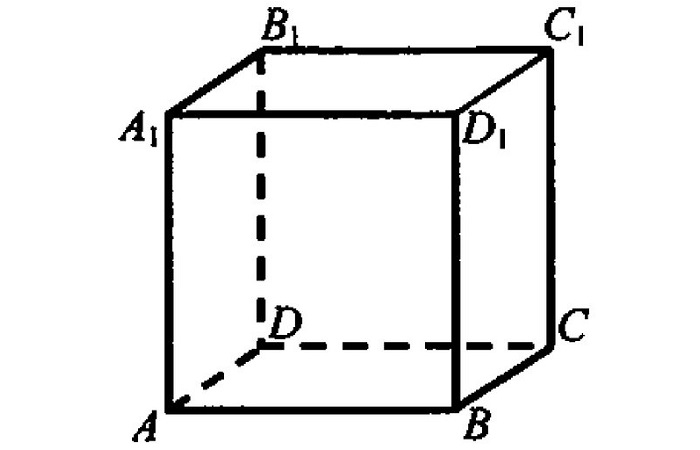
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны.
Свойства куба:
2. Противоположные грани попарно параллельны.
3. Все двугранные углы куба – прямые.
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
1. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$-высота(она же боковое ребро);
$S_<п.п>$-площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
Пирамида
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Формулы вычисления объема и площади поверхности правильной пирамиды.
В основании лежат правильные многоугольники, рассмотрим их площади:
Задачи на нахождение объема составного многогранника:
Задачи на нахождение площади поверхности составного многогранника.
— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
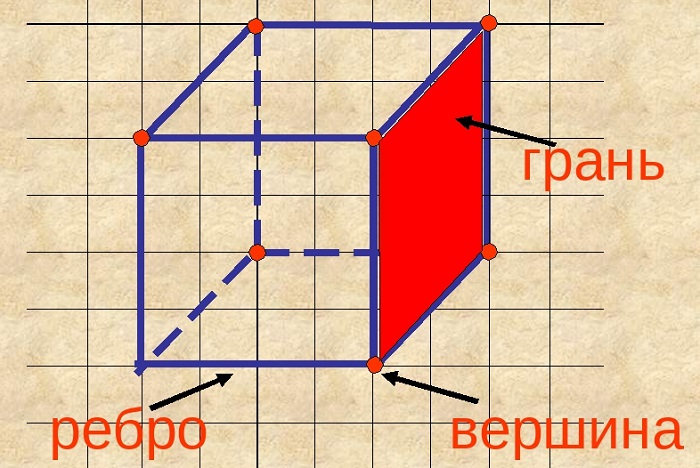
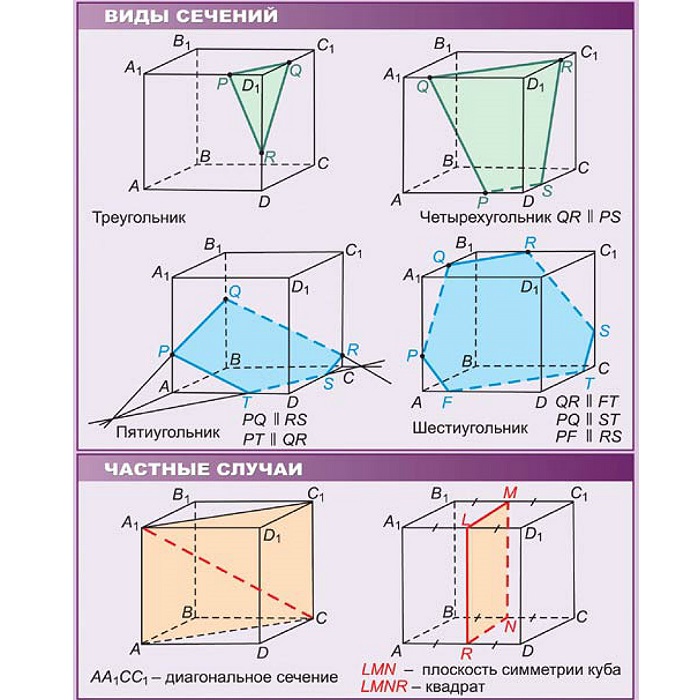
Геометрические фигуры. Куб.
Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты.
Куб является частным случаем параллелепипеда и призмы. 4 сечения куба имеют вид правильных
шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.
В кубе насчитывается шесть квадратов. Все вершины куба являются вершинами 3-х квадратов. То есть,
сумма плоских углов у каждой вершины = 270º.
Число сторон у грани – 4;
Общее число граней – 6;
Число рёбер примыкающих к вершине – 3;
Общее число вершин – 8;
Общее число рёбер – 12;

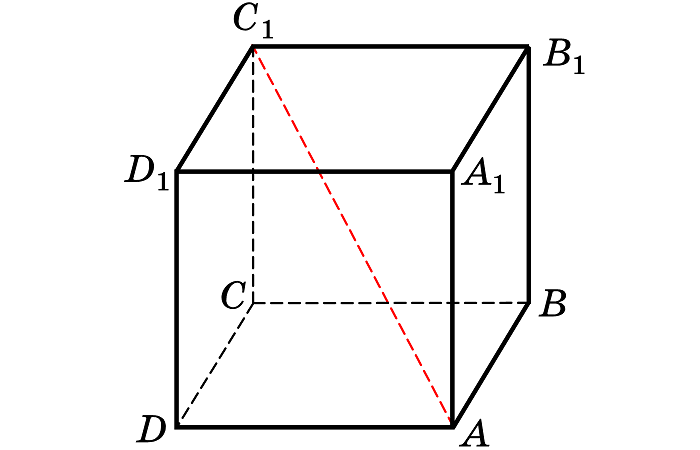
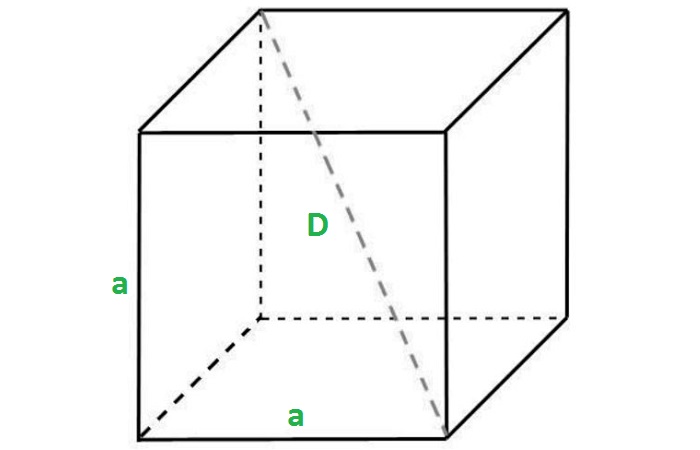
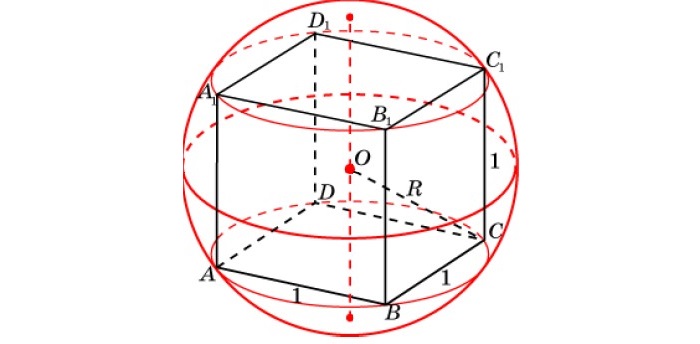
Предположим, что а – длина стороны куба, а d — диагональ, тогда:
Диагональ куба – это отрезок, который соединяет 2 вершины, которые симметричны относительно центра
Свойства куба.
перпендикулярно четырём его главным диагоналям.
совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба. В 1-м
случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной
из вершин куба. Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно
противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от
6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра
располагается на 6-ти гранях куба.
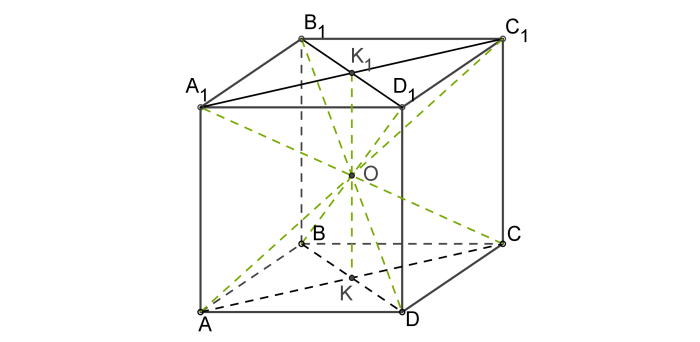
Элементы симметрии куба.
Ось симметрии куба может пролегать или сквозь середины ребер, которые
параллельны, не принадлежащих одной из граней, или сквозь точку
пересечения диагоналей противолежащих граней. Центром симметрии
куба будет точка пересечения диагоналей куба.

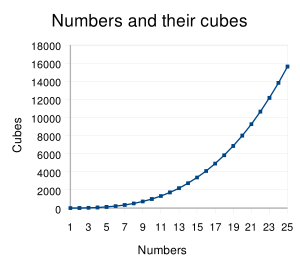

 положительных натуральных чисел вычисляется по формуле:
положительных натуральных чисел вычисляется по формуле: