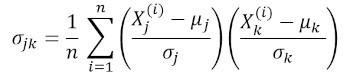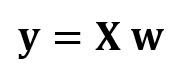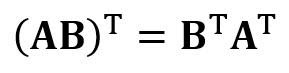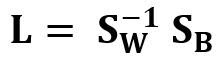Линейная алгебра что это

Рубрика: Линейная алгебра

Линейная алгебра – это раздел математики, в рамках которого изучаются самые разнообразные объекты линейной природы. В числу таких объектов относят линейные уравнения и пространства, отображения и т.д.

Основным объектом линейной алгебры является линейное пространство — понятие, обобщающее:

Элементы линейного пространства называют векторами, обобщая термин из векторной алгебры. Само линейное пространство часто называют векторным.

Линейные пространства — один из самых распространенных математических объектов, и применение линейной алгебры далеко не исчерпывает векторной и матричной алгебрами.

В линейном пространстве действуют две операции:

Однако могут вводиться и другие операции и соответственно дополнительные аксиомы. Эти операции задают дополнительные отношения в линейном пространстве, которые тоже изучаются в линейной алгебре и часто используются в различных приложениях.

Среди базовых инструментов линейной алгебры можно назвать матрицы и определители, а также сопряжение. В разделе «Линейная алгебра» на нашем сайте можно найти основные определения, кроме того, примеры с подробным решением, а также видеоуроки. Если не нашли нужную тему, или есть трудности с решением каких-то типовых задач — пишите об этом в комментариях.

Перечень тем курса линейной алгебры

Ранг матрицы

Рангом матрицы А называется наибольший из порядков ее миноров, не равных нулю. Обозначается ранг матрицы: r(A) или rang(A). Методы нахождения ранга матрицы Суще.

Правило треугольника

Общая формула вычисления определителя матрицы 3 на 3 довольно громоздка. Поэтому для вычисления определителя 3 порядка существует метод под названием — пр.

Метод Жордана — Гаусса

Этот метод заключается в следующем: расширенную матрицу системы путем элементарных преобразований нужно привести к ступенчатому виду. К элементарным преобразова.

Источник

Нежное введение в линейную алгебру

Дата публикации 2018-01-26

Что такое линейная алгебра?

Хотя линейная алгебра является большой областью со многими эзотерическими теориями и открытиями, инструментальные средства и обозначения, взятые из этой области, полезны для практиков машинного обучения. Имея прочную основу линейной алгебры, можно сосредоточиться только на хороших или соответствующих деталях.

В этом уроке вы узнаете, что такое линейная алгебра с точки зрения машинного обучения.

После завершения этого урока вы узнаете:

Обзор учебника

Этот урок разделен на 4 части; они есть:

Линейная алгебра

Подобные уравнения являются линейными в том смысле, что они описывают линию на двумерном графе. Линия происходит от вставки различных значений в неизвестный x, чтобы узнать, что уравнение или модель делает со значением y.

Мы можем выстроить систему уравнений одинакового вида с двумя или более неизвестными; например:

Столбец значений y может быть взят в качестве вектора столбца выходных данных уравнения. Два столбца значений с плавающей точкой являются столбцами данных, скажем, a1 и a2, и могут быть приняты в качестве матрицы A. Два неизвестных значения x1 и x2 могут быть взяты в качестве коэффициентов уравнения и вместе образуют вектор неизвестных б предстоит решить. Мы можем написать это компактно, используя линейную алгебраическую запись как:

Проблемы этой формы обычно сложно решить, потому что есть больше неизвестных (здесь у нас есть 2), чем есть уравнения для решения (здесь у нас есть 3). Кроме того, часто не существует ни одной прямой, которая могла бы безошибочно удовлетворить все уравнения. Системы, описывающие проблемы, которые нас часто интересуют (например, линейная регрессия), могут иметь бесконечное число решений.

Это дает небольшой вкус самой сути линейной алгебры, которая интересует нас как практиков машинного обучения. Большая часть остальных операций посвящена тому, чтобы сделать эту проблему и проблемы, такие как ее, легче понять и решить.

Численная линейная алгебра

Применение линейной алгебры в компьютерах часто называют числовой линейной алгеброй.

«Численная» линейная алгебра действительно применяется линейной алгеброй.

Это больше, чем просто реализация операций линейной алгебры в библиотеках кода; это также включает в себя тщательное решение проблем прикладной математики, таких как работа с ограниченной точностью вычислений с плавающей запятой цифровых компьютеров.

Компьютеры хороши в выполнении вычислений линейной алгебры, и большая часть зависимости от графических процессоров (GPU) с помощью современных методов машинного обучения, таких как глубокое обучение, обусловлена ​​их способностью быстро вычислять операции линейной алгебры.

Эффективные реализации векторных и матричных операций изначально были реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большая часть кода или кода, портированного из этих реализаций, лежит в основе большей части линейной алгебры, выполняемой с использованием современных языков программирования, таких как Python.

Три популярные библиотеки числовой линейной алгебры с открытым исходным кодом, которые реализуют эти функции:

Часто, когда вы прямо или косвенно вычисляете операции линейной алгебры с помощью алгоритмов более высокого порядка, ваш код, скорее всего, склоняется к использованию одной из этих или подобных библиотек линейной алгебры. Название одной из этих базовых библиотек может быть вам знакомо, если вы установили или скомпилировали любую из числовых библиотек Python, таких как SciPy и NumPy.

Линейная алгебра и статистика

Линейная алгебра является ценным инструментом в других областях математики, особенно в статистике.

Обычно студенты, изучающие статистику, ожидают увидеть по крайней мере один семестр линейной алгебры (или прикладной алгебры) на уровне бакалавриата.

Влияние линейной алгебры важно учитывать, учитывая фундаментальные отношения, которые обе области имеют с областью прикладного машинного обучения.

Некоторые четкие отпечатки линейной алгебры на статистике и статистических методах включают в себя:

Как видите, современная статистика и анализ данных, по крайней мере, в том, что касается интересов специалиста по машинному обучению, зависят от понимания и инструментов линейной алгебры.

Приложения линейной алгебры

Поскольку линейная алгебра является математикой данных, инструменты линейной алгебры используются во многих областях.

В своей классической книге на тему «Введение в линейную алгебру«Гилберт Странг приводит главу, посвященную применению линейной алгебры. В нем он демонстрирует конкретные математические инструменты, основанные на линейной алгебре. Вкратце они:

Другое интересное применение линейной алгебры состоит в том, что это тип математики, используемый Альбертом Эйнштейном в некоторых частях его теории относительности. Конкретно тензоры и тензорное исчисление. Он также ввел в физику новый тип обозначений линейной алгебры, называемый обозначениями Эйнштейна, или соглашением Эйнштейна о суммировании.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

статьи

Похожие сообщения

Резюме

В этом уроке вы обнаружили нежное введение в линейную алгебру с точки зрения машинного обучения.

В частности, вы узнали:

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Источник

Линейная алгебра: пробный заезд

Аналит, линейка, линал — эти слова ассоциируются скорее с фразой «сдать и забыть», а не с тем, для чего на самом деле нужен замечательный раздел математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и разберемся, что же в нем хорошего и почему он так полезен в приложениях.

Часто первое знакомство с линейной алгеброй выглядит как-то так:

Не очень вдохновляет, правда? Сразу возникает два вопроса: откуда это все взялось и зачем оно нужно.

Начнем с практики

Когда я занимался вычислительной гидродинамикой (CFD), один из коллег говорил: «Мы не решаем уравнения Навье-Стокса. Мы обращаем матрицы.» И действительно, линейная алгебра — «рабочая лошадка» вычислительной математики:

Попробую проиллюстрировать эту связь на более простом примере, чем гидродинамика.

Пусть у нас есть тонкий металлический стержень с закрепленными концами, температура которых поддерживается равной нулю. Начнем греть стержень с помощью распределенного источника тепла, выделяющего q(x) Джоулей в секунду на единицу длины стержня в окрестности точки x. Какая температура t=t(x) установится? Сделаем очень грубый набросок модели. Когда установится равновесие, для каждого отрезка [x-h, x+h] нашего стержня приток тепла от источника должен быть равен сумме потоков тепла через границы отрезка. Если h достаточно мало, то с точностью до констант (в которые войдет h, да простят мне это читатели) это равенство можно записать так:

где Q_x-h — поток тепла через левую границу, а Q_x+h — через правую. Согласно закону Фурье тепловой поток пропорционален разности температур (ведь если нырнуть в бассейн, то в первые секунды будет холоднее всего). Поэтому (с точностью до констант, содержащих h)

где мы уже учли граничные условия, а q_i=q(x_i). Ну вот мы и получили систему линейных уравнений:

В качестве еще одного примера приведу известную задачу о ссылочном ранжировании страниц одного сайта (или интернета в целом).
Есть N страниц, каждая из которых может содержать ссылки на другие страницы. Требуется определить, какие страницы являются наиболее важными. Как именно измерять «важность» — часть задачи. Мы будем представлять ее количественно в виде неотрицательного числа (веса). Начнем с естественного предположения: чем больше ссылок на данную страницу, тем больше ее вес. В этом подходе есть следующий недостаток: мы не учитываем вес ссылающихся страниц. Логично, что ссылка со страницы, имеющий больший вес, должна иметь большее значение. Эти рассуждения приводят нас к такой модели:

где a_ij — количество ссылок на i-ую страницу с j-ой, разделенное на общее количество ссылок с j-й страницы. Эту формулу можно читать так: вес i-й страницы равен сумме произведений веса j-й страницы на долю ссылок с j-й страницы на i-ую. Таким образом, мы свели нашу задачу к системе линейных уравнений. Более того, вектор весов p оказывается собственным вектором матрицы A, отвечающим собственному значению 1:

Существование этого вектора (строго говоря, для немного модифицированной матрицы A) гарантируется теоремой Фробениуса-Перрона. А найти его можно методом простых итераций.

Итак, линейная алгебра — это очень универсальный набор идей и инструментов, которые можно применять в самых разных областях. Но бесплатен только сыр в мышеловке, и за универсальность приходится платить: некоторые определения и теоремы могут показаться излишне абстрактными и запутанными. Но это не так: на самом деле, многие абстракции призваны упрощать жизнь, а не усложнять ее. «Если это выглядит как утка, плавает как утка и крякает как утка, то, вероятно, это утка» — по сути абстракция, причем весьма удобная, если к ней привыкнуть. То же самое с линейной алгеброй. Чтобы проиллюстрировать этот момент немного конкретнее, давайте дополним наш «внешний осмотр» кратким обсуждением того, что внутри.

Теперь немного теории

Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство в другое. В основном рассматриваются линейные функции (удовлетворяющие соотношению f(α · x + β · y) = α · f(x) + β · f(y) для любых чисел α и β и любых векторов x и y). Бывают и нелинейные (например, квадратичные формы). Но прежде всего нужно понимать что такое вектор (и векторное пространство). И это не так тривиально, как могло бы показаться.

В учебниках и курсах обычно приводится абстрактное определение из 8 пунктов. Еще иногда говорят, что векторное пространство — это аддитивно записанная абелева группа в которой определено умножение на скаляры, удовлетворяющее 4 аксиомам. Но тем, кто впервые изучает линейную алгебру, это вряд ли поможет разобраться. Гораздо проще рассмотреть несколько конкретных примеров, и увидеть в них аналогию. А определение из 8 пунктов — всего лишь формализация этой аналогии. Поэтому перейдем сразу к примерам.

Знакомые всем со школы направленные отрезки конечно же являются векторами. Множество направленных отрезков — пример векторного пространства. Теперь рассмотрим многочлены. Их можно складывать друг с другом и умножать на числа. Обратите внимание: с точки зрения алгебры эти операции сложения многочленов и умножения многочлена на число работают точно по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) выполняется как для направленных отрезков, так и для многочленов. Поэтому множество многочленов является векторным пространством, а многочлены — векторами.

Если векторы не являются линейно зависимыми, то они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и компланарных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.)

Теперь у нас есть строгое определение координат. Но смысл не только в этом: по пути мы столкнулись с более фундаментальными (и менее заметными) понятиями линейной комбинации и линейной зависимости. А еще мы узнали что в n-мерном линейном пространстве не может быть больше, чем n линейно независимых векторов. Этот факт — один из краеугольных камней линейной алгебры.

Казалось бы, мы все еще знаем слишком мало, чтобы извлечь из этого хоть какую-то пользу. Однако уже сейчас мы можем решать задачи, на первый взгляд не имеющие отношения к линейной алгебре. Например, такую: даны многочлены p и q; существует ли многочлен от двух переменных R=R(x,y) такой, что R(p(t), q(t))=0 при всех t?

Тем временем наш «пробный заезд» подходит к концу. Но остается еще коротко обсудить различные способы изучения линейной алгебры. Ограничусь здесь небольшим обзором своего собственного опыта и попробую дать на основе него пару советов.

Википедия Книга — лучший источник знаний

Мое знакомство с линейной алгеброй началось с самостоятельного изучения книги О.В. Мантурова и Н.М. Матвеева «Курс высшей математики», когда я учился в школе. Эта книга — далеко не лучший (но и не худший) источник знаний в данной области. Просто она стала первым учебником по высшей математике, попавшим в мои руки, и ее содержание показалась мне более интересным, чем школьная программа. Хотя сейчас можно с уверенностью сказать: есть куча других книг, которые школьникам стоит (и будет не менее интересно) изучить в первую очередь. Например, «Как решают нестандартные задачи» (Канель-Белов А.Я., Ковальджи А.К.) или «Ленинградские математические кружки» (Генкин С.А., Итенберг И.В., Фомин Д.В.). Если же Вы возьметесь изучать линейную алгебру по книгам, то стоит запастись терпением: для достижения желаемого результата может потребоваться больше времени, чем кажется.

Своими основными знаниями линейной алгебры (и многих других разделов математики) я все же обязан Л.И. Коваленко — легендарному преподавателю МФТИ, семинары и консультации которой всегда собирали аншлаг. Сложно переоценить то внимание, которое она оказывала каждому студенту, до позднего вечера принимая задания и так называемые «карточки» — индивидуальные задачи. А еще во время этих сдач мы активно общались друг с другом. Все это позволяло не только быстрее освоить то, что написано в учебниках, но и то, чего там нет — интуицию, хитрые приемы и прочее.

Живое общение студентов с преподавателями (и друг с другом) ничто не заменит, и в этом преимущество традиционных курсов. Но когда я сам работал ассистентом и вел семинары, часто возникало желание некоторые вещи автоматизировать, чтобы на содержательное общение оставалось больше времени. Нужно ли студенту ждать встречи с преподавателем, чтобы получить стандартный ответ на стандартный вопрос? Или узнать правильно ли решена такая-то стандартная задача? Впрочем, не нужно недооценивать студентов: по большей части, они сами хорошо чувствуют когда делают «почти бессмысленную работу», и их это тоже демотивирует. Проверка доказательства или метода решения — это одно, но вот, скажем, проверку решения системы линейных уравнений можно практически полностью доверить компьютеру. Более того, во многих случаях можно автоматизировать не только проверку ответа, но и часть самого решения — например, элементарные преобразования матриц.

Источник

Линейная алгебра для Data Science и Machine Learning

Линейная алгебра в Data Science и Machine Learning является основополагающей. Новички, начинающие свой путь обучения в области Data Science, а также признанные практики должны развить хорошее понимание основных понятий линейной алгебры.

Специально к новому старту курса математика и Machine Learning для Data Science делимся переводом статьи Бенджамина Оби Тайо — физика, кандидата наук и преподавателя Data Science — о том, что нужно знать, чтобы лучше понимать Data Science и Machine Learning.

Линейная алгебра — это раздел математики, который чрезвычайно полезен в Data Science и машинном обучении. Владение линейной алгеброй — это также самый важный математический навык в машинном обучении. Большинство моделей машинного обучения могут быть выражены в матричном виде. Сам набор данных часто представляется в виде матрицы. Линейная алгебра используется при предварительной обработке данных, в преобразовании данных и оценке моделей. Вот темы, с которыми вы должны быть знакомы:

В этой статье мы проиллюстрируем применение линейной алгебры в Data Science и Machine Learning с использованием набора данных рынка технологических акций, который можно найти здесь.

Линейная алгебра для предварительной обработки данных

Мы начнём с иллюстрации того, как линейная алгебра применяется для предварительной обработки данных.

Импорт необходимых библиотек линейной алгебры

Чтение набора данных и отображение признаков

Функция data.shape позволяет нам узнать размерность нашего набора данных. В этом случае набор данных содержит 5 признаков (date, AAPL, TSLA, GOOGL и AMZN) и каждый содержит 11 наблюдений. Дата (date) относится к торговым дням в апреле 2021 года (до 16 апреля). AAPL, TSLA, GOOGL и AMZN — это цены закрытия акций Apple, Tesla, Google и Amazon соответственно.

Визуализация данных

Чтобы выполнить визуализацию данных, нужно определить столбцовые матрицы визуализируемых признаков:

Рисунок 1. Цена акций Tesla за первые 16 дней апреля 2021 года.

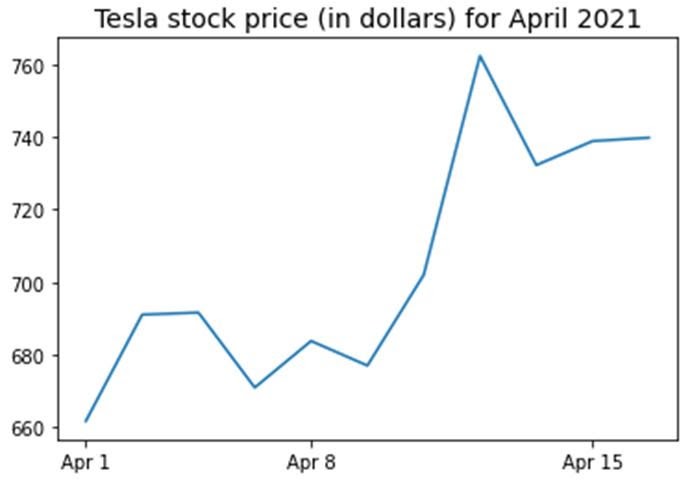
Ковариационная матрица

Ковариационная матрица является одной из наиболее важных матриц в Data Science и Machine Learning. Она предоставляет информацию о совместном движении (корреляции) между признаками. Предположим, у нас есть матрица признаков с 4 признаками и n наблюдениями, как показано в таблице 2:

Таблица 2. Матрица признаков с 4 переменными и n наблюдениями

Чтобы визуализировать корреляции между признаками, мы можем сгенерировать диаграмму рассеяния:

Рисунок 2. Парная диаграмма рассеяния для выбранных технологических акций.

где μ и σ — среднее значение и стандартное отклонения признака соответственно. Это уравнение указывает, что при нормализации признаков матрица ковариации представляет собой просто точечное произведение между признаками. Ковариационная матрица может быть выражена в виде вещественной и симметричной матрицы 4 х 4:

Эта матрица может быть преобразована в диагональную путём выполнения унитарного преобразования, также называемого преобразованием анализа главных компонентов (PCA), чтобы получить следующее:

Поскольку след матрицы при унитарном преобразовании остаётся инвариантным, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X₁, X₂, X₃ и X₄.

Вычисление ковариационной матрицы для технологических акций

Обратите внимание, что при этом используется транспонирование нормализованной матрицы.

Визуализация ковариационной матрицы

Из рисунка 3 видно, что AAPL сильно коррелирует с GOOGL и AMZN и слабо с TSLA. TSLA обычно слабо коррелирует с AAPL, GOOGL и AMZN, в то время как AAPL, GOOGL и AMZN сильно коррелируют друг с другом.

Вычисление собственных значений ковариационной матрицы

Мы наблюдаем, что, как и ожидалось, след ковариационной матрицы равен сумме собственных значений.

Вычисление кумулятивной дисперсии

Поскольку след матрицы остаётся инвариантным при унитарном преобразовании, мы наблюдаем, что сумма собственных значений диагональной матрицы равна общей дисперсии, содержащейся в признаках X₁, X₂, X₃ и X₄. Следовательно, мы можем определить следующие величины:

fig:

Обратите внимание, что когда p = 4, кумулятивная дисперсия, как и ожидалось, становится равной 1.

Из кумулятивной дисперсии (cum_var) мы видим, что 85 % дисперсии содержатся в первом собственном значении и 11 % — во втором. Это означает, что при реализации PCA могут использоваться только первые два основных компонента, поскольку 97 % общей дисперсии приходятся на эти 2 компонента. Это может существенно уменьшить размерность пространства признаков (с 4 до 2), когда реализован PCA.

Матрица линейной регрессии

Предположим, у нас есть набор данных, который имеет 4 признака предиктора и n наблюдений, как показано ниже.

Таблица 3. Матрица признаков с 4 переменными и n наблюдениями. Столбец 5 — целевая переменная (y)

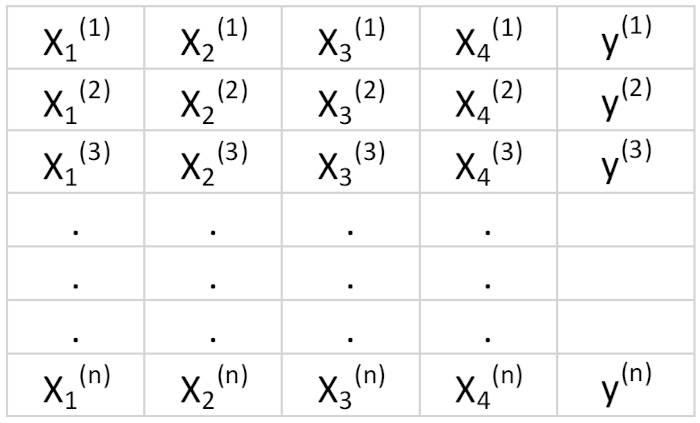
Мы хотели бы построить модель множественной регрессии для прогнозирования значений y (столбец 5). Таким образом, наша модель может быть выражена так:

В матричном виде это уравнение можно записать так:

где X — матрица признаков (n x 4), w — матрица (4 x 1), представляющая определяемые коэффициенты регрессии, и y — матрица (n x 1), содержащая n наблюдений целевой переменной y.

Обратите внимание, что X является прямоугольной матрицей, поэтому мы не можем решить приведённое выше уравнение, взяв обратную X величину.

Чтобы преобразовать X в квадратную матрицу, мы умножаем левую и правую части нашего уравнения на транспонирование из X, то есть:

Это уравнение можно записать так:

является матрицей регрессии (4×4). Мы наблюдаем, что R — это вещественная и симметричная матрица. Обратите внимание, что в линейной алгебре транспонирование произведения двух матриц подчиняется следующему соотношению:

Теперь, когда мы сократили нашу задачу регрессии и выразили её в терминах (4×4) вещественной, симметричной и обратимой матрицы регрессии R, легко показать, что точное решение уравнения регрессии выглядит так:

Примеры регрессионного анализа для прогнозирования непрерывных и дискретных переменных приведены ниже:

Основы линейной регрессии для абсолютных новичков.

Построение перцептронного классификатора с помощью метода наименьших квадратов.

Матрица линейного дискриминантного анализа

Другим примером реальной и симметричной матрицы в Data Science является матрица линейного дискриминантного анализа (LDA). Эта матрица может быть выражена так:

Где S_W — матрица рассеяния в пределах признака (the within-feature scatter matrix), а S_B — матрица рассеяния между признаками. Поскольку обе матрицы S_W и S_B вещественны и симметричны, из этого следует, что L также вещественна и симметрична. Диагонализация L создаёт подпространство признаков, которое оптимизирует раздельность классов и уменьшает размерность. Следовательно, LDA является алгоритмом обучения с учителем, а PCA — нет.

Чтобы узнать больше о реализации LDA, пожалуйста, ознакомьтесь со следующими ссылками:

Машинное обучение: уменьшение размерности с помощью линейного дискриминантного анализа.

Репозиторий GitHub для реализации LDA с использованием набора данных Iris.

Машинное обучение Python от Себастьяна Рашки, 3-е изд. (глава 5).

Резюме

Итак, мы обсудили несколько применений линейной алгебры в Data Science и машинном обучении. Используя набор данных рынка технологических акций, мы проиллюстрировали важные понятия, такие как размер матрицы, столбцовые матрицы, квадратные матрицы, ковариационные матрицы, транспонирование матрицы, собственные значения, точечные произведения и т. д.

Линейная алгебра является важным инструментом в Data Science и машинном обучении. Таким образом, новички, интересующиеся Data Science, должны ознакомиться с основными понятиями линейной алгебры.

Чтобы в деталях разобраться с внутренней механикой Data Science, не оставив без внимания машинное обучение, вы можете присмотреться к нашему курсу математика и Machine Learning для Data Science, где опытные менторы и эксперты в своём деле ответят на сложные вопросы, устранят неясности и правильно направят ваши размышления, чтобы в дальнейшем вы решали сложные проблемы самостоятельно.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

Источник