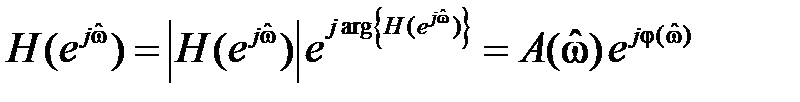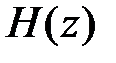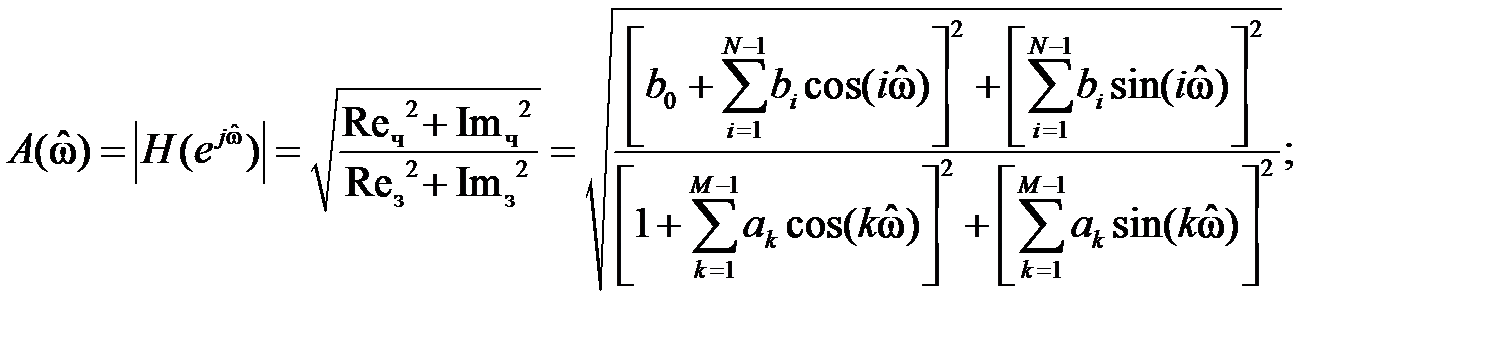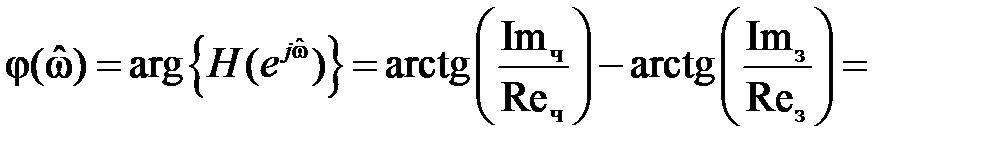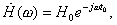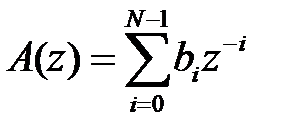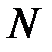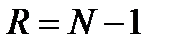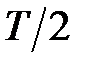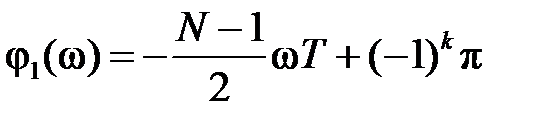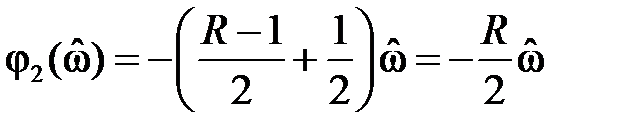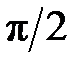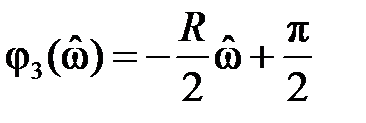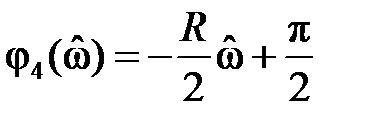Линейная фчх означает что вносится
Физический смысл ФЧХ и групповой задержки. Свойство линейности ФЧХ фильтра
Введение
Ранее мы рассмотрели структуры цифровых фильтров и их характеристики. Мы рассмотрели понятия амплитудно-частной (АЧХ), фазочастотной (ФЧХ) характеристик, а также понятие групповой задержки фильтра. В данной статье мы проанализируем физический смысл ФЧХ и групповой задержки. Рассмотрим свойство фильтров с линейной ФЧХ и получим условия линейности ФЧХ цифрового фильтра.
Очень часто при расчете цифровых фильтров ставится задача обеспечить постоянную групповую задержку или линейную фазочастотную характеристику (ФЧХ). В данной статье речь пойдет именно о фильтрах с линейной ФЧХ, и будут получены условия при которых цифровой фильтр будет иметь строго линейную фазочастотную характеристику.
Также вводят понятие групповой задержки как производной от ФЧХ:
Смысл групповой задержки можно пояснить следующим образом. Отклик физически реализуемого фильтра всегда возникает не раньше воздействия, при этом фильтр задерживает входной сигнал при фильтрации на некоторое время. При этом если подавать на фильтр сигналы разной частоты, то сигнал на выходе одного и того же фильтра могут быть задержаны на разное время. Эта задержка выражается в сдвиге фазы сигнала на выходе относительно сигнала на входе. Групповая задержка при этом характеризует изменение временного сдвига сигнала, который получается в результате фазового сдвига. Проиллюстрируем это рисунком 1.
Рисунок 1: Взаимосвязь фазового и временного сдвига сигнала
Если ФЧХ линейна, то групповая задержка постоянна, т.е. при изменении частоты сигнала она не меняется.
При нелинейной ФЧХ разные частоты приобретают разные фазовые сдвиги и соответственно разные временные задержки на выходе фильтра. Чтобы понять это проведем следующий эксперимент.
Пусть имеется сигнал, у которого во времени меняется мгновенная частота. В качестве такого можно взять сигнал с фазовой модуляцией (PM) вида:
| Рисунок 2: Фильтрация PM сигнала при помощи фильтра с линейной ФЧХ | Рисунок 3: Фильтрация PM сигнала при помощи фильтра с нелинейной ФЧХ |
| Рисунок 4: PM cигнал на выходе фильтра с линейной ФЧХ при компенсации задержки | Рисунок 5: PM cигнал на выходе фильтра с нелинейной ФЧХ при компенсации задержки |
Из рисунка 4 следует, что сигнал на выходе фильтра полностью повторяет сигнал на входе (разумеется небольшие амплитудные искажения есть из-за неидеальности фильтра, но для нас самое главное, что фаза исходного сигнала и выходного сигнала совпадают). При этом выходной сигнал был сдвинут по оси времени для устранения постоянной задержки фильтра. Из рисунка 5 можно заметить, что скомпенсировать задержку невозможно, поскольку она меняется при изменении мгновенной частоты сигнала. Так компенсация задержки при высокой мгновенной частоте (в интервале от 100 до 150 мкс) фаза сигналов при низкой мгновенной частоте (в интервале от 50 до 100 мкс) не совпадает. Таким образом нелинейная ФЧХ фильтра привела к фазовым искажениям нашего сигнала, хотя амплитудные искажения минимальны так как АЧХ фильтра выбрана таким образом, чтобы сигнал не искажался.
Приведенный пример наглядно показывает, что нелинейная ФЧХ фильтра искажает сигнал и это надо учитывать, поскольку например при когерентной обработке искажения фазы недопустимы.
Теперь когда понятна необходимость использования фильтров с линейной ФЧХ мы исследуем свойства импульсных характеристик, которые обеспечивают эту самую линейную ФЧХ.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Групповая задержка фильтра и ее расчёт
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Аналоговые и цифровые фильтры характеризуются передаточными характеристиками и соответственно, которые могут быть записаны как рациональные функции комплексных переменных и :
АЧХ и ФЧХ аналогового фильтра:
Для гармонического синусоидального сигнала фазовый сдвиг соответствует временно́му сдвигу, как это показано на рисунке 1.
Задержанный сигнал можно представить как:
Мы можем формально рассмотреть приращения:
Продемонстрируем это на примере.
Пусть также дан отсчёт гармонического сигнала на нормированной частоте :
Из характеристик фильтра, приведенных на рисунке 2 можно видеть, что фазовая задержка фильтра на частоте тестового сигнала равна отсчётов, а групповая задержка отсчётов, что почти в два раза выше фазовой задержки.
Пропустим сигнал через данный эллиптический фильтр и проанализируем сигнал на выходе фильтра, показанный на рисунке 3б сплошной линией. Можно видеть, что выходной сигнал задержан относительно входного.
Рассмотрим теперь задержку треугольной огибающей на выходе фильтра, как это показано с увеличением масштаба на рисунке 3г. Можно видеть, что треугольная огибающая задержана на величину групповой задержки отсчётов.
При передачи информации гармоническое колебание не является информационным, поэтому на практике величина группового времени запаздывания является более часто используемым параметром, так как именно оно определяет задержку информационной огибающей при прохождении сигнала через фильтр.
Расчет групповой задержки на основе численного дифференцирования ФЧХ согласно (12) бывает затруднительно ввиду наличия разрывов ФЧХ, как это показано на рисунке 3. В результате дифференцирования возникают выбросы в групповой задержке, которые мешают анализу.
Для улучшения качества расчёта группового времени запаздывания можно использовать алгоритм, приведенный в данном параграфе для цифрового БИХ-фильтра.
Комплексный коэффициент передачи цифрового БИХ-фильтра имеет вид:
Понятие линейно-фазовых фильтров
Линейная фазовая характеристика, также известная как постоянное групповое время задержки, является важным свойством в некоторых применениях фильтров. Рассмотрим понятие линейной фазовой характеристики чуть подробнее.
В большинстве обсуждений фильтров акцент делается на амплитуду. Если нам требуется сглаживание для АЦП, нам нужен фильтр нижних частот, то есть схема, которая поддерживает (или увеличивает) амплитуду низкочастотных сигналов и уменьшает амплитуду высокочастотных сигналов. Если мы удаляем из аудиосигнала смещение по постоянному напряжению, мы используем фильтр верхних частот, но при этом мы должны убедиться, что частота среза достаточно низка, чтобы избежать уменьшения амплитуды сигнала на частотах, которые мы хотим услышать.
Однако важно помнить, что фильтры влияют не только на амплитуду сигнала, но и на его фазу.
Например, простейший RC-фильтр нижних частот вносит в выходной синусоидальный сигнал сдвиг фазы выходной синусоиды до 90° относительно входного синусоидального сигнала. Предлог «до» в предыдущем предложении очень важен – фактический сдвиг фазы зависит от частоты сигнала, проходящего через фильтр, как показано на следующем графике сдвига фазы в зависимости от частоты для RC-фильтра нижних частот с частотой среза 1 кГц.
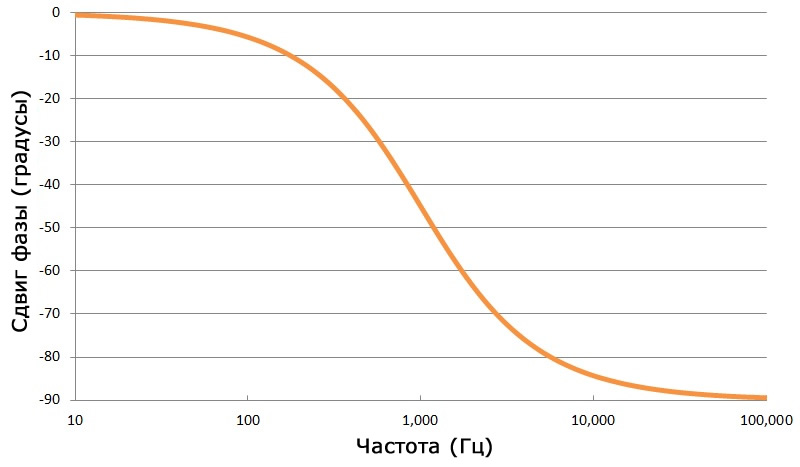
Теперь рассмотрим ситуацию, в которой на фильтр будут подаваться сигналы, состоящие из разных частот, которые работают вместе. Если эти разные частоты испытывают разные задержки, могут возникнуть проблемы. Вот два примера:
На данный момент ситуация может показаться безнадежной – глядя на график выше, мы ясно видим, что фазовый сдвиг резко меняется в зависимости от частоты. Но есть критически важный момент, который меняет всё: мы должны помнить, что в зависимости от частоты изменяется и временной эквивалент, соответствующий конкретному фазовому сдвигу. Рассмотрим следующую диаграмму:
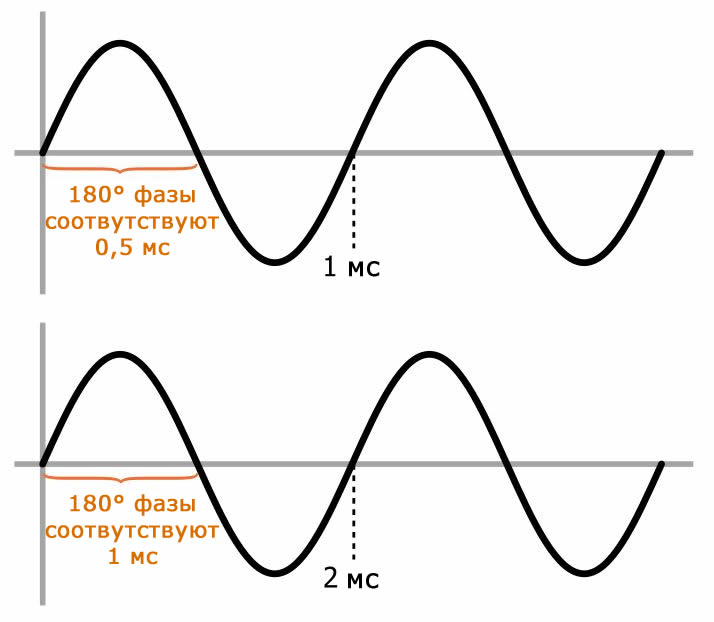
Здесь мы видим два синусоидальных сигнала, один с частотой 1 кГц (то есть период = 1 мс) и один с частотой 500 Гц (то есть период = 2 мс). Конкретный сдвиг фазы (в качестве примера на диаграмме используется 180°) для каждой частоты соответствует разному значению времени: разные частоты соответствуют разным периодам, а сдвиг фазы соответствует определенной части периода.
Из этого следует, что поддержание синхронизации между различными частотными компонентами сигнала не означает принудительного обеспечения одинакового сдвига фазы, поскольку одинаковый сдвиг фазы на разных частотах приведет к различным временным задержкам.
Чтобы добиться равных временных задержек для всех частот, нам нужно, чтобы каждая частота имела свой сдвиг фазы, а именно сдвиг фазы, который приводит на конкретной частоте к задержке, равной задержке на других частотах. Более конкретно, нам нужен сдвиг фазы, который линейно увеличивается по мере увеличения частоты. Это имеет смысл, поскольку при увеличении частоты фиксированный сдвиг фазы соответствует постепенно уменьшающемуся отрезку времени, и, таким образом, для компенсации нам нужен больший сдвиг фазы.
Таким образом, идеальный линейно-фазовый фильтр демонстрирует сдвиг фазы, который линейно увеличивается по мере увеличения частоты, и, таким образом, он обеспечивает постоянную временную задержку (это, главным образом, относится к частотам в полосе пропускания, то есть к частотам, интересующим разработчика). Групповое время задержки пропорционально производной фазо-частотной характеристики по частоте. Производная линейной функции является константой, что объясняет, почему линейная фазо-частотная характеристика также соответствует постоянному групповому времени задержки. Хорошо известной топологией схем, оптимизированной для получения линейного фазового отклика, является фильтр Бесселя.
Линейная фчх означает что вносится
Вид ФЧХ является одним из важнейших показателей фильтра при принятии решения о его пригодности для конкретного приложения. ФЧХ позволяет определить временную задержку, вносимую в сигнал.
Линейная и нелинейная ФЧХ
Фильтр с линейной ФЧХ задерживает все частоты на одно и то же время. Следовательно, выходной сигнал не искажается, а лишь задерживается на соответствующее время. Поскольку реальный сигнал содержит много частот, задержка каждой частоты на разное время приводит к искажению выходного сигнала.
В некоторых приложениях, таких как музыка или видео, нелинейная ФЧХ недопустима.
Линейная ФЧХ исключительно важна в полосе пропускания, поскольку это тот диапазон, в котором происходит выделение интересующих нас частотных составляющих сигнала. Обычно имеет место компромисс между линейной ФЧХ в полосе пропускания и другими требованиями к фильтру, такими как крутизна спада и затухание в полосе задерживания.
Практически используемые аналоговые фильтры
Существует много схем аналоговых фильтров с различными характеристиками АЧХ и ФЧХ. Рассмотрим более подробно фильтр Баттерворта.
Этот тип фильтра обычно называют «максимально гладким» вследствие плавности АЧХ в полосе пропускания. У фильтров Баттерворта действительно нет пульсаций в полосе пропускания, однако им присущи два недостатка:
1. Нелинейная ФЧХ в полосе пропускания исключает их применение в тех приложениях, где требуется линейная ФЧХ. График группового времени прохождения (ГВП) (1) в нормированной шкале частот иллюстрирует нелинейность ФЧХ. Нормированная частота среза при этом равна f/f c = 1.0. Задержка, вносимая в сигнал, существенно увеличивается, когда значение нормированной частоты приближается к частоте среза.
2. В переходной полосе АЧХ фильтра Баттерворта имеет пологий спад. Для того, чтобы достичь заданной крутизны спада, потребуется каскадное соединение большого числа звеньев. На графике представлено семейство АЧХ для фильтров Баттерворта различного порядка.
В основе проектирования фильтров Бесселя лежат функции Бесселя. Эти фильтры имеют ФЧХ, лучшую, чем у фильтров Баттерворта и Чебышева. Однако спад АЧХ в переходной полосе у них значительно менее крутой (более пологий).
Из сравнения данных фильтров становится ясным, что существует противоречие между более крутым спадом АЧХ и линейностью ФЧХ (гладкостью ГВП). На практике в большинстве случаев фильтры Баттерворта обеспечивают удовлетворительный компромисс.
Пакеты программ для проектирования фильтров
Проектирование фильтров – это задача, требующая трудоемких вычислений по формулам, идеально подходящая для машинных расчетов. В пакетах программ процесс проектирования фильтров формализуется и тем самым повышается эффективность проектирования. Используя один из таких пакетов, можно легко спроектировать фильтр, задав совокупность требований, таких как тип фильтра, частота среза, уровень пульсаций в полосе пропускания и требуемая скорость спада.
Пакет программ обычно позволяет вычислить величины всех компонентов схемы фильтра, а также АЧХ и ФЧХ. Проектировщик может затем оценить пригодность фильтра и изменить некоторые требования к нему без реального этапа конструирования. Это одно из главных преимуществ использования пакетов программ.
Теперь рассмотрим цифровые фильтры на простом примере фильтра скользящего среднего. Определим входной и выходной сигналы, а также основные компоненты цифрового фильтра.
Весовые коэффициенты и отводы фильтра
Выход умножителей подсоединяется к сумматорам, которые суммируют задержанные взвешенные значения отсчетов.
Выходной сигнал y(n)
Выходной сигнал цифрового фильтра представляет собой комбинацию соответствующего количества задержанных и взвешенных отсчетов.
Работа цифровых фильтров
Теперь рассмотрим, как можно вычислить выходной сигнал y(n), исходя из того, о чем мы только что узнали. Обозначим через x(n) текущий отсчет, соответствующий n-ому отсчету в последовательности. Предыдущие отсчеты можно при этом обозначить как x(n-1) = задержке x(n) на единицу времени, x(n-2) = задержке x(n) на две единицы времени и т. д. При поступлении текущего отсчета x(n) на вход с отводов подаются задержанные отсчеты на умножители с коэффициентами a 1 и a 2. Следовательно, в любой момент дискретизации значение выходного сигнала может быть вычислено как взвешенная сумма текущего и двух предыдущих отсчетов
Какой функциональной зависимости соответствует данное уравнение?
Работа фильтра на практике
Мы уже выбрали следующие коэффициенты фильтра:
Такие коэффициенты были выбраны для того, чтобы обеспечить хорошее качество усреднения цен на акцию. Несколько позже в этой лекции мы обсудим, как вычисляют коэффициенты по заданным требованиям к характеристикам и техническим условиям, используя пакет программ.
Рассмотрим работу фильтра на простых данных. Мы выберем данные фондовой биржи – ежедневно изменяющиеся цены на акцию. Все цены в США измеряются в долларах ($). На втором графике показано изменение цены акции, фиксируемое (дискретизируемое) ежедневно с понедельника по воскресенье включительно. Как можно видеть на графике, основные изменения произошли в четверг и пятницу.
Полагая, что предыдущие отсчеты входного сигнала отсутствовали, т.е. начальные условия нулевые, вычислим выходной сигнал фильтра. В течение понедельника единственным входным отсчетом, который оказывал воздействие на выходной сигнал, был отсчет понедельника, поэтому y(0) = 5. Во вторник становится одним входным отсчетом больше. Учитывается отсчет понедельника, в данном случае с единичной задержкой и весовым коэффициентом 0.5. Суммируем его с отсчетом вторника, взятым с весовым коэффициентом 0.25, в результате чего получаем y(1) = 15. В течение среды необходимо учесть уже все три взвешенных входных отсчета (один текущий и два задержанных), соответственно y(2) = 20.
y(3) = 0.25*12 + 0.5*20 + 0.25*20 = 18,
y(4) = 0.25*40 + 0.5*12 + 0.25*20 = 21.
Теперь можно добавить недостающие значения, вычисленные в паузе, на кривую графика. Фильтр действительно обеспечивает вычисление скользящего среднего. На этом простом примере демонстрируются основные принципы работы цифровых фильтров. Для расчета выходных сигналов фильтра выполняется последовательность операций умножения с накоплением (МАС). Такие операции свидетельствуют о важности команды МАС в ЦПОС.
(1) Групповое время прохождения определяется формулой ГВП = d(ФЧХ)/dw. Прим. ред.
(2) Стоит напомнить, что у фильтров Баттерворта пульсации в полосе пропускания отсутствуют. Прим. ред.
(3) На самом деле пульсациями у фильтров Чебышева можно управлять, выбирая их величину по желанию. При этом уменьшение пульсаций приводит к уменьшению крутизны спада. Чтобы сохранить крутизну при малых пульсациях приходится увеличивать порядок фильтра. Прим. ред.
Определение и свойства частотных характеристик ЛСД
Комплексную функцию 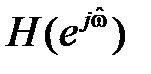
Комплексной частотной характеристикой 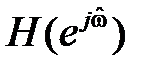
Амплитудно-частотной характеристикой 
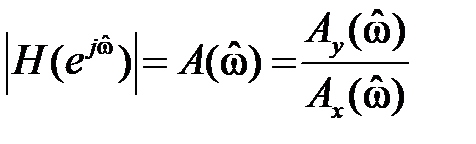
Фазочастотной характеристикой 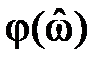
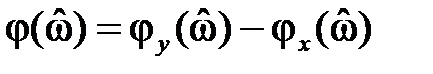
Свойства частотных характеристик определяются свойствами комплексной экспоненты и тригонометрических функций: sin, cos, tg и arctg.
2. Непрерывность: КЧХ, АЧХ и ФЧХ — непрерывные (или кусочно-непрерывные) функции частоты по определению.
3. Периодичность: ЧХ, АЧХ и ФЧХ — периодические функции частоты с периодом, равным частоте дискретизации 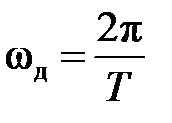
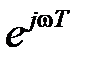

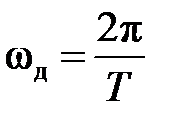
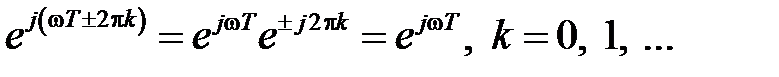
Соответственно, период ЧХ, АЧХ и ФЧХ в зависимости от используемой шкалы частот будет равен:
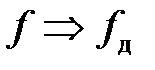
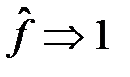
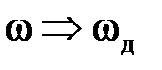
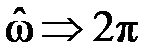
3. Чётность АЧХ и нечётность ФЧХ.
Если коэффициенты ПФ являются вещественными (а другие случаи мы не рассматриваем), то модуль частотной характеристики (АЧХ) является чётной, а аргумент (ФЧХ) — нечётной функцией частоты:

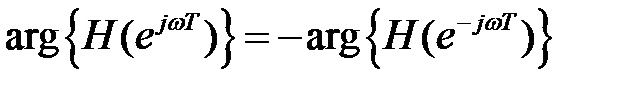
Вычисление частотных характеристик ЛДС
Получить КЧХ путём замены 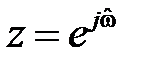
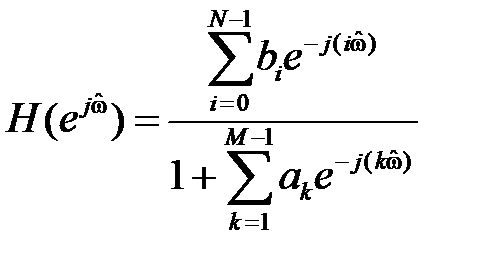


Выделить вещественные и мнимые части в числителе (с индексом ‘ч’) и знаменателе (с индексом ‘з’) КЧХ 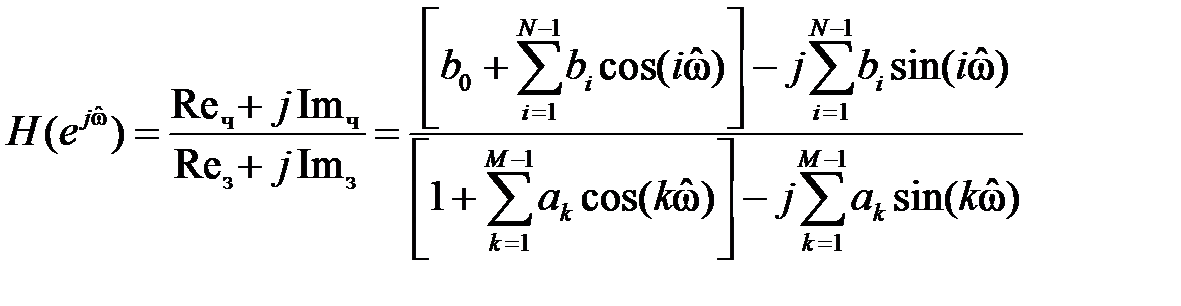
Записать АЧХ и ФЧХ, исходя из их определений:
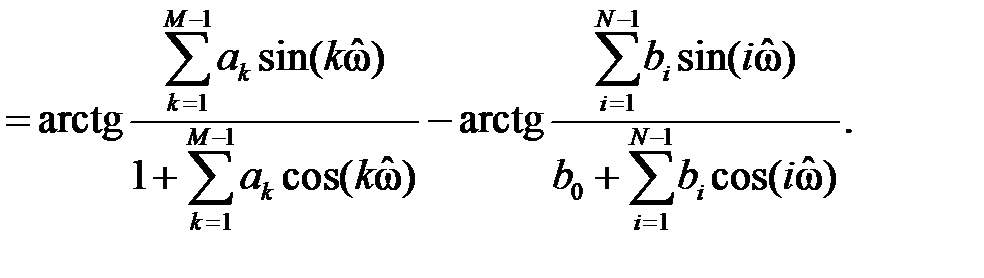
19 Классификация цифровых фильтров
По полосе пропускания.
20. Условия неискаженной передачи сигнала линейным четырехполюсником.
Сигнал проходит через линейную цепь без искажений, если форма его на выходе не меняется, но могут измениться только его величина и положение на оси времени. Это возможно только в случае равномерной амплитудно-частотной передаточной характеристики и линейной фазо-частотной характеристики цепи, т.е. если
то спектральная плотность выходного сигнала будет равна
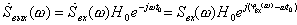
что означает, что модуль спектральной плотности выходного сигнала пропорционален модулю спектральной плотности входного сигнала на всей оси частот, а в фазе входного сигнала появился дополнительный пропорциональный частоте сдвиг на (wt0), что означает задержку (при t0>0) сигнала на выходе на время t0.
21.Пример существования КИХ-фильтров с линейной ФЧХ.
Пример 1.Построим структурную схему фильтра при 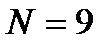
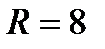
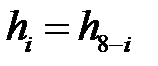 или или 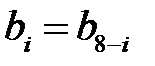 . . |
Решение. Таким условиям соответствует фильтр типа 1 (см. табл. 1), передаточная функция которого имеет вид:
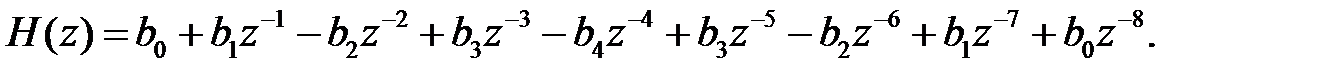 |
Объединим члены передаточной функции, имеющие одинаковые коэффициенты:
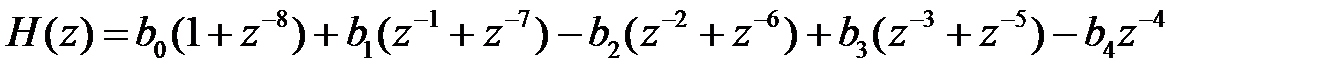 . . |
Полученную передаточную функцию и соответствующую ей схему будем называть приведёнными.
Рис. 2.2. Приведённая структурная схема КИХ-фильтра типа 1 порядка 8
Приведённая передаточная функция имеет 5 сложений, в то время как в прямой схеме всего одно сложение, и 5 умножений, в то время как в прямой было 9, т. е. число умножителей в структурной схеме (рис. 2.2) сократилось практически в 2 раза.
Для приведённых структур КИХ-фильтров типа 1 число умножителей оказывается равным 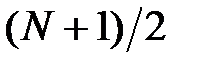
Примечание
Приведенная структура КИХ-фильтра типа 3, имеющего нечетное 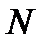
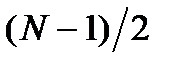
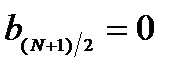
Пример 2.
Построим приведенную структурную схему фильтра при 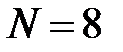
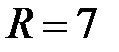
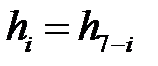 или или 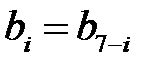 . . |
Решение. Таким условиям соответствует фильтр типа 2 (см. табл. 18.1), передаточная функция которого имеет вид:
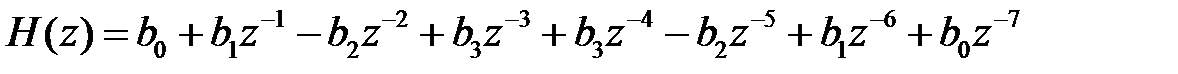 . . |
Поступим так же, как в предыдущем примере; тогда получим приведенную передаточную функцию:
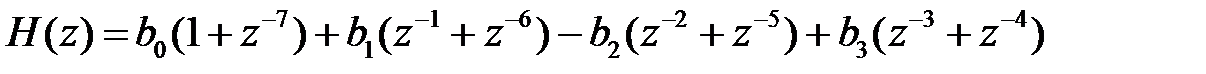 , , |
у которой число умножений ровно в 2 раза меньше по сравнению с обычной прямой структурой; поэтому количество умножителей в приведенной структурной схеме (рис. 2.3) также сократилось вдвое.
Рис. 2.3. Приведенная структурная схема КИХ-фильтра типа 2
Примечание
Приведенные структуры КИХ-фильтров типов 2 и 4, имеющих чётное 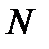
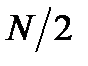
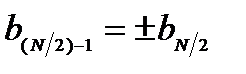
22. Утверждение о КИХ-фильтрах с линейной ФЧХ
Цифровой КИХ-фильтр с передаточной функцией
обладает строго линейной ФЧХ с точностью до скачков на 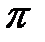
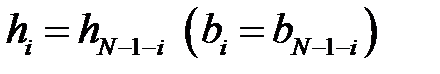
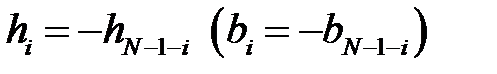
причём ФЧХ имеет вид:
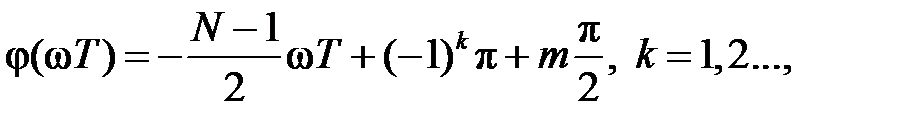
где k – номер частоты 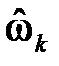
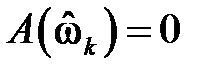
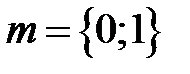
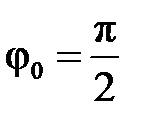
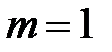
Следствие 1.Скачки ФЧХ на 
На рис. 2.1 показаны варианты линейной ФЧХ фильтра нижних частот при 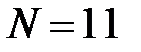
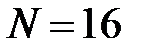
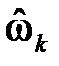
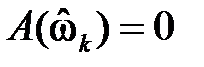
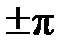
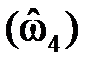
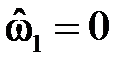
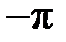
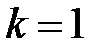
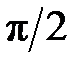
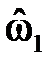
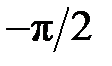
Следствие 2.Групповое время задержки (замедления, прохождения) фильтра с линейной ФЧХ постоянно и равно

причем в зависимости от значения 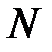
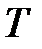
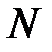
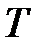
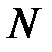
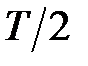
Длина импульсной характеристики (число коэффициентов)
Порядок фильтра
Импульсная характеристика
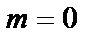
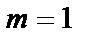
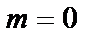
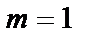
Рис. 2.1. Построение линейной ФЧХ КИХ-фильтра при 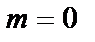
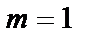
Следствие 3.В зависимости от чётности или нечётности порядка (соответственно нечётности и чётности длины импульсной характеристики), а также от симметричности или антисимметричности коэффициентов передаточной функции (отсчетов импульсной характеристики) существуют четыре типа КИХ-фильтров с линейными ФЧХ, что показано в табл. 1.
Таблица 1. Типы КИХ-фильтров с линейной ФЧХ
Следствие 4.Свойства симметричности коэффициентов передаточной функции (импульсной характеристики) КИХ-фильтров с линейной ФЧХ дают возможность построить структурные схемы, число умножителей в которых практически в 2 раза меньшеумножителей, нежели структурные схемы КИХ-фильтров с произвольной ФЧХ, т. е. практически в 2 раза меньше порядка фильтра: если порядок чётный (длина нечётная), то количество умножителей оказывается строго в два раза меньше порядка
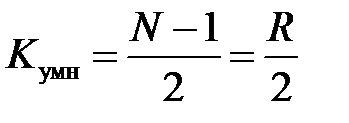
при нечётном порядке (чётной длине) количество умножителей составит
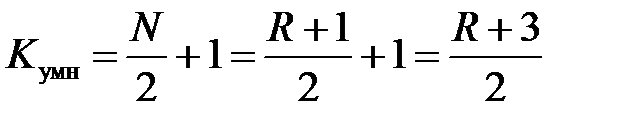
Уменьшение числа умножителей приводит, во-первых, к увеличению быстродействия и, во-вторых, к существенному уменьшению собственного шума фильтра, а потому и к увеличению его динамического диапазона.
23. Типы КИХ-свойства КИХ-фильтров типа 1:
Возможна реализация фильтров произвольной избирательности (низкочастотной, высокочастотной, полосовой, режекторной, многочастотной), а также цифровых амплитудных корректоров.
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации
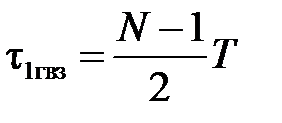
свойства КИХ-фильтров типа 2:
Возможна реализация только низкочастотных и полосовых фильтров.
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу с половиной периодов дискретизации 
свойства КИХ-фильтров типа 3:
Возможна реализация только полосовой избирательности. Однако поскольку ФЧХ на всех частотах сохраняет сдвиг на 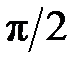
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации
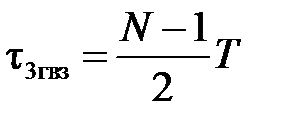
свойства КИХ-фильтров типа 4:
Возможна реализация фильтров только высокочастотной и полосовой избирательности. Однако, поскольку ФЧХ на всех частотах сохраняет сдвиг на 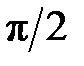
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации 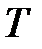
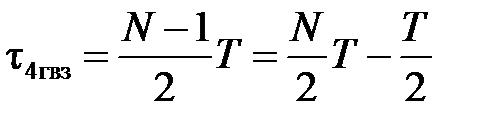
ОБЪЯСНЕНИЕ К СВОЙСТВАМ:
Прежде чем изучать свойства КИХ-фильтров, отметим, что их комплексные частотные характеристики можно представить в следующем виде:
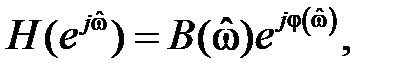
где 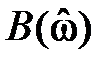
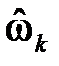
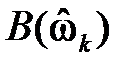
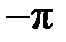
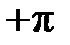
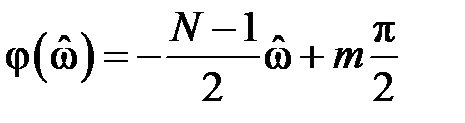

Замечание: весь дальнейший материал можно излагать на конкретных числовых примерах, приводимых в Приложении к данной лекции, что определяется самим лектором.
КИХ-фильтры типа 1имеют нечётную длину 
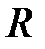
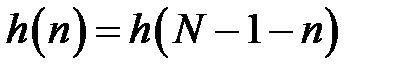
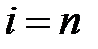
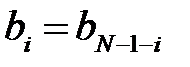
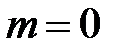
и групповое время задержки
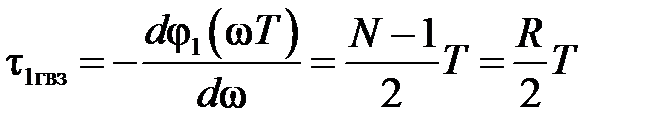
равное целому числу периодов дискретизации.
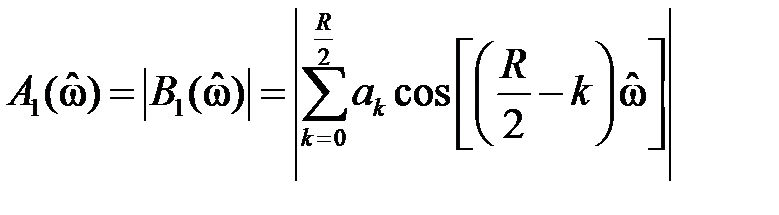
где 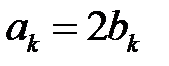
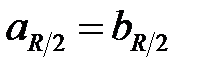
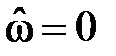
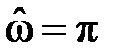
на частоте 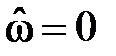
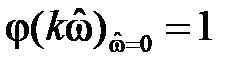
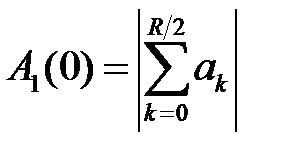
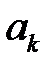
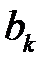
на частоте 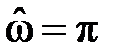
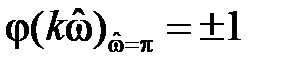

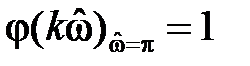
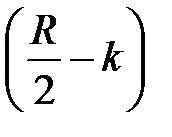
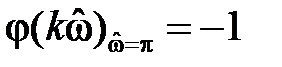
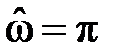
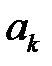

Проанализируем фазочастотную характеристику:
начальная фаза 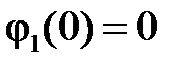
набег фазы (с учетом ее скачков на 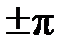

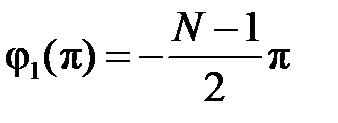
если количество скачков чётное, и
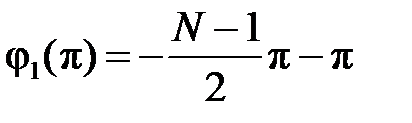
если количество скачков нечётное.
Замечание: Вместо АЧХ можно рассмотреть конкретные примеры, приведённые на прилагаемых рисунках.
Из вышесказанного вытекают свойства КИХ-фильтров типа 1:
Возможна реализация фильтров произвольной избирательности (низкочастотной, высокочастотной, полосовой, режекторной, многочастотной), а также цифровых амплитудных корректоров.
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации
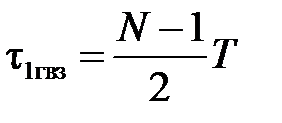
КИХ-фильтры типа 2имеют чётную длину 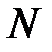
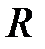

и групповое время задержки
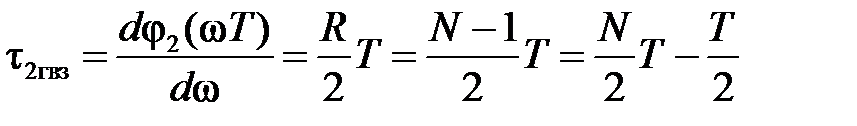
равное целому числу периодов дискретизации плюс половина периода; например, при
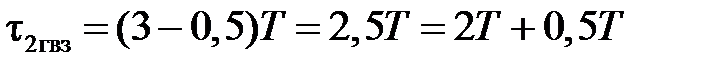
Обозначив 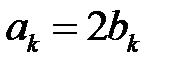
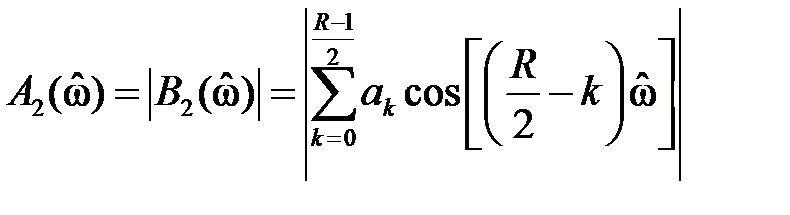
Вновь проанализируем АЧХ на частотах 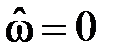

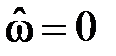
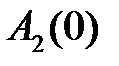
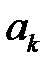
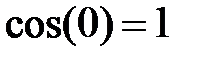
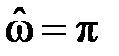
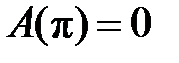
Действительно, аргумент косинуса содержит разность целого числа 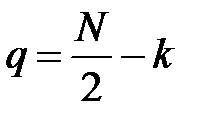

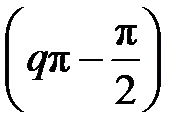
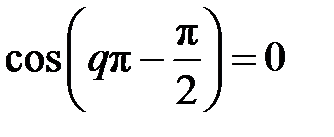
Из формулы ФЧХ следует:
начальная фаза 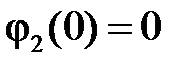
набег фазы (с точностью до ее скачков на 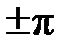

если количество скачков чётное, и целое число 
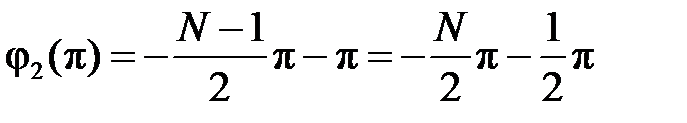
если количество скачков нечётное.
Из вышесказанного вытекают свойства КИХ-фильтров типа 2:
Возможна реализация только низкочастотных и полосовых фильтров.
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу с половиной периодов дискретизации 
КИХ-фильтры типа 3имеют нечётную длину 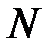

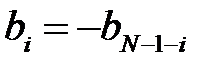
и групповое время задержки
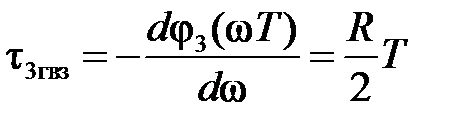
равное целому числу периодов дискретизации.
Амплитудно-частотная характеристика имеет вид:
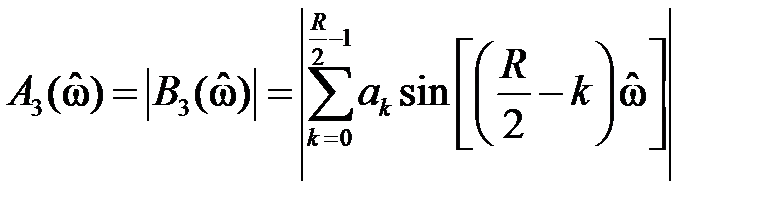
(где коэффициент 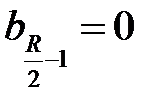
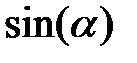
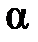
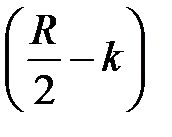
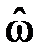
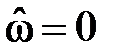
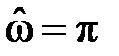
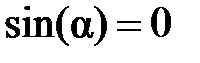

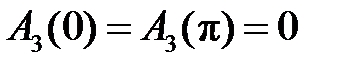
что говорит о невозможности конструирования на базе фильтров типа 3 низкочастотных, высокочастотных и режекторных фильтров.
Поэтому рассматриваемые фильтры могут быть только полосовыми.
Из формулы ФЧХ с учетом скачков фазы на 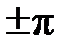
начальная фаза 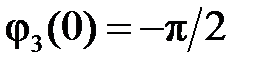
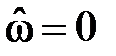
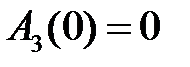
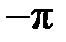
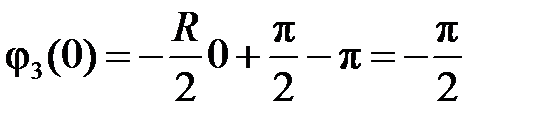
набег фазы (относительно начальной фазы) в основной полосе частот составляет целое число 
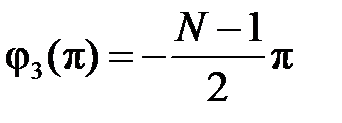
если количество скачков (включая скачки на частотах и 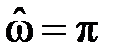
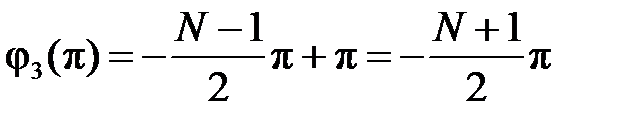
Из вышесказанного вытекают свойства КИХ-фильтров типа 3:
Возможна реализация только полосовой избирательности. Однако поскольку ФЧХ на всех частотах сохраняет сдвиг на 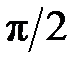
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации
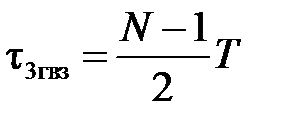
КИХ-фильтры типа 4имеют чётную длину 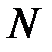
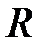
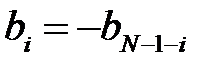
и групповое время задержки, аналогично ГВЗ фильтра типа 2,
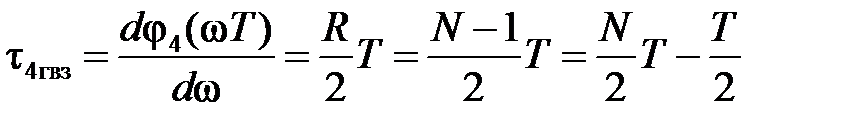
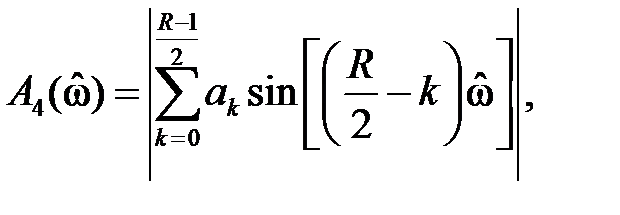
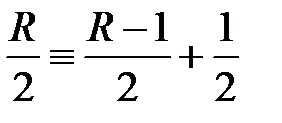
Запишем аргумент синуса в эквивалентной форме:
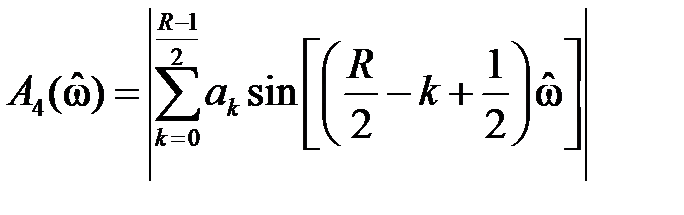
тогда легко видеть, что
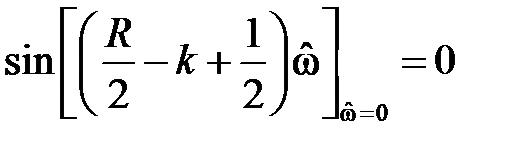
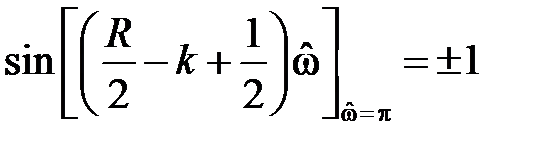
поэтому 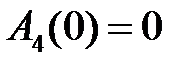
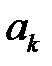
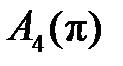
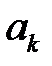
Из формулы ФЧХ с учётом скачков фазы на 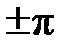
начальная фаза 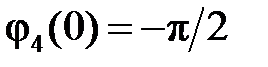
набег фазы (относительно начальной фазы) в основной полосе частот составляет
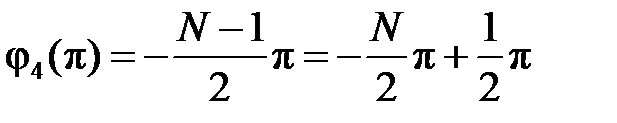
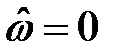
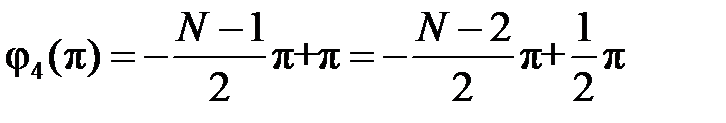
Из сказанного вытекают свойства КИХ-фильтров типа 4:
Возможна реализация фильтров только высокочастотной и полосовой избирательности. Однако, поскольку ФЧХ на всех частотах сохраняет сдвиг на 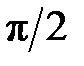
Задержка сигнала на выходе фильтра относительно сигнала на его входе равна целому числу периодов дискретизации 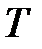
Дата добавления: 2018-08-06 ; просмотров: 772 ; Мы поможем в написании вашей работы!