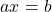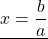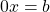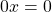Линейные уравнения что это такое
Линейное уравнение
теория по математике 📈 уравнения
Уравнение – это равенство, содержащее переменную, значение которой надо найти.
Уравнение с одним неизвестным, содержащим первую степень, называется линейным уравнением с одной переменной. Стандартный вид линейного уравнения ax+b=0, где a и b некоторые числа, а х – переменная. Также стандартным видом уравнения можно считать и вид ax=b.
Так, например, к линейным относятся уравнения:
6х+21=0; 34–2х=0; 34х=17; 89х=0
Уравнения, содержащие несколько слагаемых с переменной или без нее, а также скобки, называются уравнениями, сводящимися к линейным. То есть при его упрощении должно получиться линейное уравнение стандартного вида. К таким уравнениям могут относиться уравнения вида:
х+12=4х–45; 19х–67=98; х=–32+17х; 7(х+13)=89–14х
Решить уравнение – это значит найти все его корни или доказать, что корней нет.
Что такое корень уравнения?
Вспомним, что корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.
Корни линейного уравнения
Наличие корней зависит от коэффициентов а и b.
Рассмотрим нахождение количества корней на примерах.
Здесь коэффициент а отличен от нуля. Значит, уравнение имеет один корень.
Здесь коэффициент а равен нулю, поэтому корней нет.
Здесь оба коэффициента равны нулю, поэтому уравнение имеет множество корней, или, еще можно сказать, что корнем уравнения является любое число.
Чтобы найти корни уравнения, надо его решить, используя алгоритм, по которому из одного уравнения мы сможем получить уравнение, равносильное данному. Сначала вспомним, что при переносе слагаемых из одной части в другую, мы получаем уравнение, равносильное данному. Также можно делить или умножать обе части уравнения на одно и то же число.
Пример №2. Решить уравнение:
В данном уравнении нет скобок, поэтому выполняем перенос слагаемых, изменяя соответственно знаки у тех слагаемых, которые переносим (обычно слагаемые с переменной собираем слева, а без переменной – справа): 2х–9х=10+11. Теперь приводим подобные слагаемые и получаем: –7х=21. Видим, что корень находится действием деления (неизвестный множитель): х=21:(–7). Ответ х=–3.
При оформлении решения запись оформляем следующим образом:
Пример №3. Решить уравнение:
Здесь мы видим скобки, поэтому сначала раскроем их, помня о том, то число 2 в левой части уравнения надо умножить на каждое слагаемое в скобках, а в правой части уравнения перед скобкой стоит «минус», поэтому изменяем знаки у слагаемых при раскрытии скобок: 5х–2х+16=9х–3х–11. Выполняем перенос слагаемых: 5х–2х–9х+3х=–11–16. Приводим подобные: –3х=–27. Находим корень уравнения: х=–27:(–3). Получаем ответ: х=9
Пример №4. Решить уравнение:
Выполним всё по алгоритму: перенос слагаемых и приведение подобных слагаемых. 2х–2х=3+12; 0х=15. Видим, что коэффициент а=0, поэтому запишем ответ – нет корней, так как надо 15:0, а мы знаем правило, что на нуль делить нельзя.
Имеем линейное уравнение:
Следовательно, начинаем решение с переноса слагаемых (с переменной влево, без переменной – вправо): 3х + 7х= – 5 – 2, не забывая изменять знак у слагаемых, которые переносим. Теперь приводим подобные в каждой части, получаем 10х= –7.
Находим неизвестный множитель делением произведения –7 на известный множитель 10, получаем –0,7.
Запись решения выглядит так:
pазбирался: Даниил Романович | обсудить разбор | оценить
Линейные уравнения
Примеры линейных уравнений:
Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение является линейным уравнением.
Примеры решения линейных уравнений:
Это линейное уравнение, так как переменная стоит в первое степени.
Попробуем преобразовать его к виду a x = b :
Для начала раскроем скобки:
− 2 x − 2 = 1 − 2 = − 1 2 = − 0,5
Это уравнение не является линейным уравнением, так как старшая степень, в которой стоит переменная x равна двум.
Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:
Это уравнение не является линейным уравнением.
Особые случаи (встречаются редко, но знать их полезно).
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:
Задания для самостоятельного решения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
2 − 3 ( 2 x + 2 ) = 5 − 4 x
Переносим иксы влево, числа вправо:
x = 9 − 2 = − 9 2 = − 4,5
№2. При каком значении x значения выражений 7 x − 2 и 3 x + 6 равны?
Решение:
Приравниваем эти два выражения:
№3. Решите уравнение ( − 5 x + 3 ) ( − x + 6 ) = 0.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Чтобы найти все корни данного уравнения, надо приравнять каждый множитель к нулю и оба корня взять в ответ.
( − 5 x + 3 ) ( − x + 6 ) = 0 ⇔ [ − 5 x + 3 = 0 − x + 6 = 0 ⇒ [ − 5 x = − 3 ; − x = − 6 ; ⇒ [ x = − 3 − 5 = 3 5 = 0,6 x = − 6 − 1 = 6 1 = 6
В задании указано, что в ответ надо записать корни в порядке возрастания 0,6 6.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение:
Раскроем квадраты, используя ФСУ (формулы сокращенного умножения):
x 2 − 2 ⋅ x ⋅ 4 + 4 2 + x 2 + 2 ⋅ x ⋅ 9 + 9 2 − 2 x 2 = 0
Замечаем, что x 2 сокращается:
x 2 − 8 x + 4 2 + x 2 + 18 x + 9 2 − 2 x 2 = 0
− 8 x + 18 x + 16 + 81 = 0
Решение:
Раскроем скобки, используя ФСУ.
( x + 10 ) 2 = ( 5 − x ) 2
x 2 + 2 ⋅ x ⋅ 10 + 10 2 = 5 2 − 2 ⋅ 5 ⋅ x + x 2
x 2 + 20 x + 100 = 25 − 10 x + x 2
x 2 + 20 x + 100 − x 2 + 10 x − 25 = 0
Решение:
Решение линейных уравнений с одной переменной
В данной статье рассмотрим принцип решения таких уравнений как линейные уравнения. Запишем определение этих уравнений, зададим общий вид. Разберем все условия нахождения решений линейных уравнений, используя, в том числе, практические примеры.
Обратим внимание, что материал ниже содержит информацию по линейным уравнениям с одной переменной. Линейные уравнения с двумя переменными рассматриваются в отдельной статье.
Что такое линейное уравнение
Такая формулировка использована в учебнике алгебры ( 7 класс) Ю.Н.Макарычева.
Примерами линейных уравнений будут:
3 · x = 11 (уравнение с одной переменной x при а = 5 и b = 10 );
В различных учебных материалах могут встречаться разные определения. К примеру, Виленкин Н.Я. к линейным относит также те уравнения, которые возможно преобразовать в вид a · x = b при помощи переноса слагаемых из одной части в другую со сменой знака и приведения подобных слагаемых. Если следовать такой трактовке, уравнение 5 · x = 2 · x + 6 – также линейное.
А вот учебник алгебры ( 7 класс) Мордковича А.Г. задает такое описание:
Примером линейных уравнений подобного вида могут быть:
Принцип решения линейных уравнений
Рассмотрим, как определить, будет ли заданное линейное уравнение иметь корни и, если да, то сколько и как их определить.
Дадим пояснение. Нам известно, что в процессе решения уравнения возможно осуществлять преобразование заданного уравнения в равносильное ему, а значит имеющее те же корни, что исходное уравнение, или также не имеющее корней. Мы можем производить следующие равносильные преобразования:
Все приведенные рассуждения дают нам возможность записать алгоритм, дающий возможность найти решение любого линейного уравнения:
Собственно, описанная последовательность действий и есть ответ на вопрос, как находить решение линейного уравнения.
Примеры решения линейных уравнений
Решение
Ответ: x – любое число.
Линейные уравнения что это такое
Теперь перейдем к чуть более сложному – линейным уравнениям с двумя переменными.
Линейные уравнения с двумя переменными имеют вид:
\( \displaystyle ax+by+c=0\), где \( \displaystyle a\), \( \displaystyle b\) и \( \displaystyle c\) – любые числа и \( \displaystyle a\ne 0\).
Как ты видишь, вся разница только в том, что в уравнение добавляется еще одна переменная. А так все то же самое – здесь нет иксов в квадрате, нет деления на переменную и т.д. и т.п.
Какой бы привести тебе жизненный пример… Возьмем того же Васю. Допустим, он решил, что каждому из 3-ех друзей он даст одинаковое количество яблок, а \( \displaystyle 2\) яблока оставит себе.
Сколько яблок нужно купить Васе, если каждому другу он даст по \( \displaystyle 1\) яблоку? А по \( \displaystyle 2\)? А если по \( \displaystyle 3\)?
Зависимость количества яблок, которое получит каждый человек к общему количеству яблок, которое необходимо приобрести будет выражена уравнением:
\( \displaystyle y=3x+2\), где
Решая эту задачу, мы получим, что если одному другу Вася даст \( \displaystyle 1\) яблоко, то ему необходимо покупать \( \displaystyle 5\) штук, если даст \( \displaystyle 2\) яблока – \( \displaystyle 8\) и т.д.
И вообще. У нас две переменные. Почему бы не построить эту зависимость на графике?
Строим и отмечаем значение наших \( \displaystyle x\), то есть точки, с координатами \( \displaystyle 1\), \( \displaystyle 2\) и \( \displaystyle 3\)!
Как ты видишь, \( \displaystyle x\) и \( \displaystyle y\) зависят друг от друга линейно, отсюда и название уравнений – «линейные».
Графическое изображение линейных и нелинейных уравнений
Абстрагируемся от яблок и рассмотрим графически различные уравнения. Посмотри внимательно на два построенных графика – прямой и параболы, заданными произвольными функциями:
Найди и отметь на обоих рисунках точки \( \displaystyle x\), соответствующие \( \displaystyle y=2\).
Что у тебя получилось?
Ты видишь, что на графике первой функции одному \( \displaystyle y\) соответствует один \( \displaystyle x\).
То есть \( \displaystyle y\) и \( \displaystyle x\) линейно зависят друг от друга, что не скажешь про вторую функцию.
Да и построенный график никак не напоминает линию, а является параболой.
Графиком линейного уравнения должна быть прямая линия.
С тем, что уравнение не будет линейным, если у нас идет \( \displaystyle x\) в какой-либо степени – это понятно на примере параболы, хотя для себя ты можешь построить еще несколько простых графиков, например \( \displaystyle y=<
Но я тебя уверяю – ни один из них не будет представлять собой ПРЯМУЮ ЛИНИЮ.
Не веришь? Построй, а затем сравни с тем, что получилось у меня:
А что будет, если мы разделим что-то на \( \displaystyle x\), например, какое-то число? Будет ли линейная зависимость \( \displaystyle y\) и \( \displaystyle x\)?
Не будем рассуждать, а будем строить! Например, построим график функции \( \displaystyle y=\frac<1>
Как-то не выглядит построенное прямой линией… соответственно, уравнение не линейное.
Что такое линейное уравнение
Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?
В курсе алгебры 7 класса линейное уравнение определяется следующим образом.
Определение.
Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.
Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:
Количество корней линейного уравнения зависит от значения a (коэффициента перед x).
При a≠0 линейное уравнение имеет единственное решение.
Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:
Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).
В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).
При a=0, b≠0 линейное уравнение
При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.
При a=0, b=0 линейное уравнение
имеет бесконечное множество решений.
При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.
Возможные решения линейных уравнений можно изобразить в виде схемы.
Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.
Решение многих уравнений сводится к решению линейных уравнений.