Луч что угол половинит 11 букв

ПОВТОРЯЕМ ТЕОРИЮ

117. Заполните пропуски.

РЕШАЕМ ЗАДАЧИ

118. Запишите названия углов, изображенных на рисунке.

119. Запишите все углы, изображенные на рисунке.

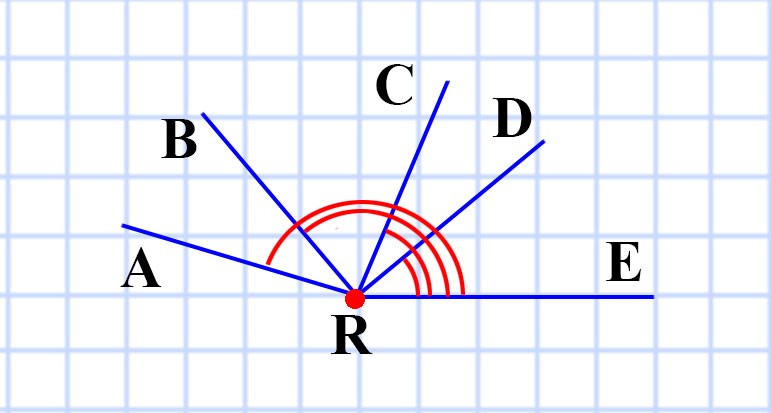
120. Из лучей, изображенных на русунке, одну из сторон угла АВС пересекают лучи:

121. Расшифруйте слово.

122. Начертите угол MKN и проведите лучи КЕ и KF между его сторонами. Запишите все образовавшиеся углы.

MKE, EKF, FKN, MKN, MKF, EKN

123. Начертите два угла так, чтобы:

1) они имели общую вершину и ощую сторону;
2) они имели общую вершину и не имели общих сторон;
3) вершина одного из углов лежала на стороне другого;
4) стороны углов пересекались только в двух точках.

124. Начертите угол АВС, отрезок DE, луч FM и проведите прямую КР так, чтобы одновременно выполнялись следующие условия:

1) прямая КР пересекает отрезок DE, луч FM и только одну сторону угла АВС.
2) отрезок DE пересекает только одну сторону угла АВС и не пересекает луч FM.
3) луч FM пересекает обе стороны угла АВС.

Источник

Мерзляк 5 класс — § 12. Виды углов. Измерение углов

Вопросы к параграфу

1. Какой угол называют развёрнутым? Развёрнутый угол — это угол, лучи которого образуют прямую и их начала совпадают.

2. В каких единицах измеряют углы? Углы измеряют в градусах (например ∠45° — это угол величиной 45 градусов).

3. Какова градусная мера развёрнутого угла? 180°

4. Что означает измерить угол? Измерить угол — это значит посчитать сколько единичных углов в нём помещаются.

5. Как называется прибор, который используют для измерения углов? Транспортир.

6. Расскажите, как пользоваться транспортиром. Для того, чтобы измерить угол транспортиром надо:

7. Какие градусные меры имеют равные углы? Равные углы имеют равные градусные меры.

8. Какой из двух неравных углов считают большим? Большим считается угол, градусная мера которого больше.

9. Каким свойством обладает величина угла? Если между сторонами угла АОС провести луч ОВ, то градусная мера угла АОС равна сумме градусных мер углов АОВ и ВОС:

∠АОС = ∠АОВ +∠ВОС, если луч ОВ лежит между сторонами угла АОС.

10. Какой угол называют острым? Острым углом называют угол, градусная мера которого меньше 90 °.

11. Какой угол называют прямым? Прямым углом называют угол, градусная мера которого равна 90°.

12. Какой угол называют тупым? Тупым углом называют угол, градусная мера которого больше 90°, но меньше 180°.

13. На какие углы делит развёрнутый угол его биссектриса? Биссектриса делит угол на два прямых угла, то есть градусная мера каждого из этих углов равна 90°.

14. В каких случаях говорят, что от данного луча отложен данный угол? Говорят, что от данного луча отложен данный угол в том случае, если дан определённый луч, например ОА, и от него построен заданный угол, например ∠АОС = 63°, причём вершиной угла является вершина заданного луча.

Решаем устно

1. Назовите два числа, одно из которых:

2. Часы спешат на 10 мин и сейчас показывают время 10 ч 8 мин. Который час на самом деле?

10 ч 8 мин — 10 мин = 9 ч 58 мин

Ответ: сейчас 9 ч 58 мин.

3. Часы отстают на 7 мин и сейчас показывают время 16 ч 55 мин. Который час на самом деле?

16 ч 55 мин + 7 мин = 17 ч 2 мин.

Ответ: сейчас 17 ч. 2 мин.

4. Какие из следующих уравнений не имеют корней:

Ответ: не имеют корней уравнения под номером 4 и 6.

5. Для озеленения улицы длиной 3 км на одной из её сторон посадили деревья на расстоянии 20 м друг от друга. Первое дерево было посажено в начале улицы, а последнее — в её конце. Сколько деревьев было посажено? Чему равно расстояние между первым и пятым деревьями?

1) 3 000 : 20 + 1 = 151 (дерево) — было посажено.

2) 20 • (5 — 1) = 20 • 4 = 80 (метров) — расстояние между 1-м и 5-м деревом.

Ответ: Было посажено 151 дерево. Между первым и пятым деревом 80 метров.

Упражнения

296. Начертите:

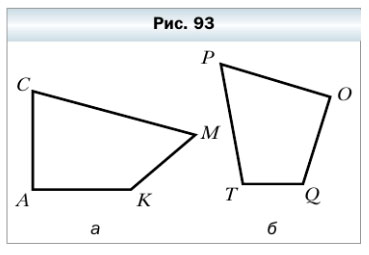
297. Найдите на рисунке 93 острые, тупые и прямые углы.

298. Какие из данных углов острые, тупые, прямые, развёрнутые: ∠А = 96°, ∠B = 84°, ∠S= 180°, ∠D=90°, ∠R = 162°, ∠E= 60°, ∠Q = 100°, ∠M= 72°?

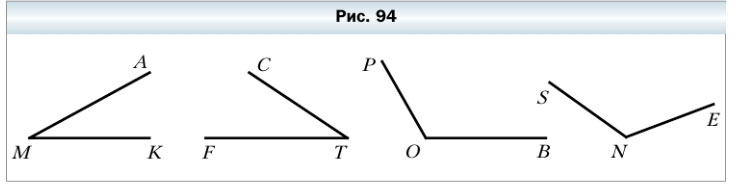
299. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 94. Определите вид каждого угла.

300. Найдите, пользуясь транспортиром, градусные меры углов, изображённых на рисунке 95. Определите вид каждого угла.

301. Начертите угол, градусная мера которого равна: 1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°; 8) 65°. Определите вид каждого угла.

302. Проведите луч. Отложите от этого луча угол, градусная мера которого равна: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Определите вид каждого из построенных углов.

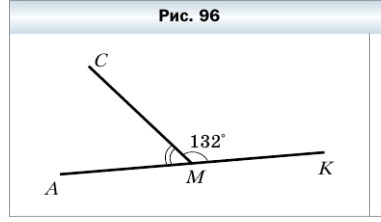
303. На рисунке 96 ∠CMK = 132°, а угол АМК — развёрнутый. Вычислите величину угла АМС.

∠АМК = 180° — развёрнутый

∠АМС = ∠АМК — ∠CMK = 180° — 132° = 48°

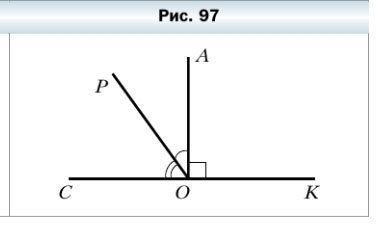
304. На рисунке 97 угол АОК — прямой, ∠POC — 54°, а угол СОК — развёрнутый. Вычислите величину угла АОР.

∠COК = 180° — развёрнутый

∠АOP = ∠COK — ∠POC — ∠AOK = 180° — 54° — 90° = 36°

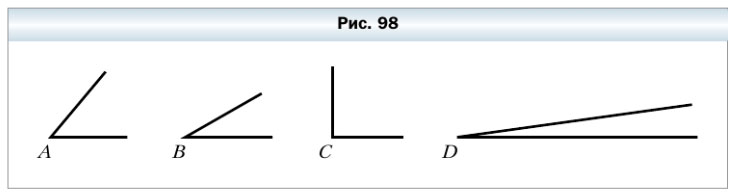
305. Какой из углов, изображённых на рисунке 98, наибольший? Наименьший?

306. Начертите угол CDE, равный 152°. Лучом DA разделите этот угол на два угла так, чтобы ∠CDA = 98°. Вычислите величину угла ADE.

∠ADE = ∠CDE — ∠CDA = 152° — 34° = 54°

307. Начертите угол ABC, равный 106°. Лучом BD разделите этот угол на два угла так, чтобы ∠ABD = 34°. Вычислите величину угла DBC.

∠DBC = ∠ABC — ∠ABD = 106° — 34° = 72°

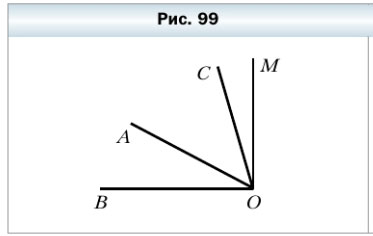
308. Из вершины прямого угла ВОМ (рис. 99) проведены два луча ОА и ОС так, что ∠BOC = 74°, ∠AOM = 62°. Вычислите величину угла АОС.

∠MOC = ∠BOM — ∠BOC = 90° — 74° = 16°

∠AOC = ∠AOM — ∠MOC = 62° — 16° = 46°

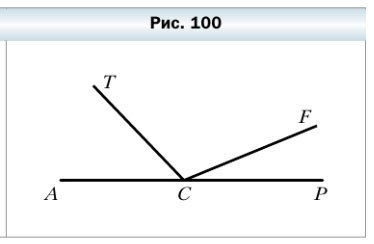
309. Из вершины развёрнутого угла АСР (рис. 100) проведены два луча СТ и CF так, что ∠ ACF = 158°, ∠ TCP = 134°. Вычислите величину угла TCF.

∠PCF = ∠ACP — ∠ACF = 180° — 158° = 22°

∠TCF = ∠TCP — ∠PCF = 134° — 22° = 112°

310. Верно ли утверждение:

1) угол, который меньше тупого, — острый. Неверно, так как меньше тупого не только острые углы, но и прямой угол.

2) угол, который меньше развёрнутого, — тупой. Неверно, так как меньше развёрнутого угла все тупые углы, все острые углы и прямой угол.

3) половина тупого угла — острый угол. Верно, так как половина даже самого большого тупого угла будет меньше 90º.

4) сумма градусных мер двух острых углов больше 90°. Неверно, так как сумма двух острых углов может быть и меньше 90°.

5) угол, который больше прямого, — тупой. Неверно, так как больше прямого могут быть как тупые углы, так и развёрнутый угол.

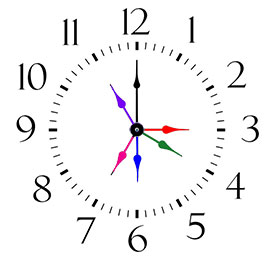
311. Найдите градусную меру утла между стрелками часов, если они показывают:

Ответ: 1) 90º, 2) 180º, 3) 120º, 4) 30º, 5) 150º.

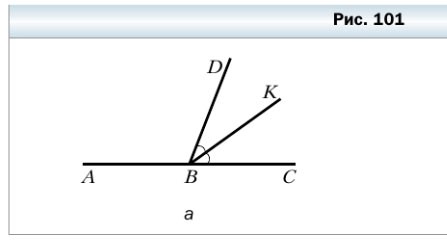
312. Луч BK является биссектрисой угла CBD, ∠ ABK = 146° (рис. 101, a). Вычислите градусную меру угла CBD.

∠ABC = 180º — развёрнутый

∠KBC = ∠ABC — ∠ABK = 180º — 146º = 34º

так как луч BK — это биссектриса ∠CBD, значит луч BK делит тот угол пополам. Мы заем, что ∠KBC = 34º. Значит:

∠CBD = ∠KBC • 2 = 34º • 2 = 68º

313. Луч ОА является биссектрисой угла СОМ, ∠ СОМ = 54° (рис. 101, б). Вычислите градусную меру угла ВОА.

так как луч OA — это биссектриса ∠COM, значит луч OA делит тот угол пополам. Мы заем, что ∠COM = 54º. Значит:

∠COA = ∠COM : 2 = 54º : 2 = 27º

∠BOC = 180º — развёрнутый

∠BOA = ∠BOC — ∠COA = 180º — 27º = 153º

314. Проведите три прямые, пересекающиеся в одной точке. Запишите все развёрнутые углы, образовавшиеся при этом.

Каждая прямая образует по 2 развёрнутых угла. Значит образовались следующие развёрнутые углы: AOD, BOE, COF, DOA, EOB, FOC.

315. Проведите шесть прямых, пересекающихся в одной точке. Верно ли, что среди образовавшихся при этом углов есть угол, градусная мера которого меньше 31°?

Каждая прямая образует по 2 развёрнутых угла. Например, прямая MH образует развёрнутые углы MOH и HOM. Каждый из этих углов равен 180º. Значит сумма углов между соседними лучами на рисунке равна 180º • 2 = 360º.

Всего образовалось 12 углов, расположенных между соседними лучами. 360º : 12 = 30º. Значит как минимум один (а на самом деле два) угла будут иметь градусную меру менее 31º.

Упражнения для повторениях

316. Заполните цепочку вычислений:

317. Верно ли неравенство (а + 253) • 7 Ответ: при а = 124 неравенство неверно, так как 2 639 > 2 435.

318. В четыре стакана помещается столько же молока, сколько и в банку. В стакан и банку помещается 1 кг 200 г молока. Сколько граммов молока помещается в стакан?

Так как в одной банке помещается столько же молока, сколько и в 4 стаканах, то в банке и стакане будет содержаться столько же молока сколько в 5 стаканах (4 + 1 = 5).

1 кг 200 г = 1 200 г

1 200 : 5 = 240 (г) — молока помещается в стакан.

319. Длина границы России с Китаем, Монголией и Казахстаном составляет 15 293 км. Найдите длину границы России с каждым из этих государств, если длина границы с Китаем и Монголией равна 7 694 км, а с Китаем и Казахстаном — 11 808 км.

1) 15 293 — 11 808 = 3 485 (км) — граница России с Монголией.

2) 7 694 — 3 485 = 4 209 (км) — граница России с Китаем.

3) 11 808 — 4 209 = 7 599 (км) — граница России с Казахстаном.

Ответ: граница России с Китаем — 4 209 км, с Монголией — 3 485 км, с Казахстаном — 7 599 км.

Задача от мудрой совы

320. Улитка за день поднимается вверх по столбу на 3 м, а за ночь съезжает по нему на 2 м вниз. На какой день она доберётся до вершины столба, высота которого равна 20 м?

Каждые сутки улитка способна подняться по столбу на 1 м:

1) 3 метра днём — 2 метра ночью = 1 метр за сутки

Но в последний день она как обычно поднимется на 3 метра, а спускаться уже не будет. Значит, за все дни, кроме последнего, улитка поднимется на 17 м:

2) 20 — 3 = 17 (метров) — преодолеет улитка за все дни, кроме последнего.

То есть ей потребуется 17 дней для преодоления 17 метров и ещё 1 день для преодоления последних 3 метров:

3) 17 : 1 + 1 = 17 + 1 = 18 (дней) — нужно улитке для того, чтобы подняться на столб.

Ответ: улитка доберётся до вершины на 18-й день.

Источник