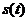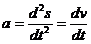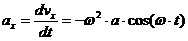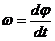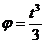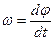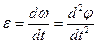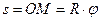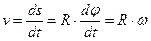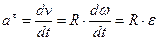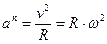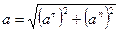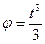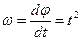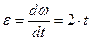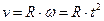Вращение маховика в период пуска машины определяется уравнением
Вращательное движение.
Дата добавления: 2014-10-04 ; просмотров: 1801 ; Нарушение авторских прав
Вращательным движением называется такое движение тв. тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
Остальные точки движутся в плоскостях перпендикулярных оси вращения и описывают окружности, центры которых лежат на оси вращения.
При вращении тела угол поворота является функцией времени,
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Уравнение равномерного вращения.
После интегрирования по времени от нуля до некоторого времени получим
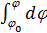

Число оборотов, совершаемых вращающимся телом за единицу времени (обычно за минуту), называется частотой вращения и обозначается буквой n.
Уравнение равнопеременного движения.
После интегрирования аналогично выше изложенному получим
Здесь под w и e, понимаются алгебраические значения соответственно угловой скорости и углового ускорения.
Уравнение (8-3) можно переписать в форме
После интегрирования получим
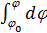

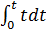
Уравнение (8-4) называется уравнением равнопеременного вращения тела.
Модуль окружной скорости точки вращающегося твердого тела
Точка вращающегося тела испытывает касательное и нормальное ускорения.
Касательное ускорение часто называют вращательным, оно равно
Нормальное ускорение направлено к центру и его обычно называют центростремительным. Его модуль равен
Модуль полного ускорения равен
Определить модуль и направление ускорения точки на радиусе R= 50 cм и мгновение, когда ее скорость равна 8 м/с.
t= w 1/2 = 16 1/2 = 4 c; e= 2*4=8 c; w e = Re= 0,5*8=4 m/c;
8.3 Плоское движение плоского тела.
Плоским или плоскопараллельным движением твердого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Плоская фигура, образованная сечением тела этой неподвижной плоскостью Q, во все время движения остается в этой плоскости (рис. 8.1).
Рассмотрим движение точек тела, расположенных на одном перпендикуляре к неподвижной плоскости Q. Точка М1 движется в плоскости Q1, а точка М2— в плоскости Q2 ; обе плоскости параллельны неподвижной плоскости Q.
При движении тела отрезок М1М2 остается перпендикулярным к исходной плоскости, т.е. остается параллельным своему начальному положению. Это значит, что все точки этого перпендикуляра аналогично точкам тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Т.к. положение плоской фигуры на плоскости вполне определяется положением двух ее точек или положением отрезка, соединяющего две точки, то положение плоской фигуры в ее плоскости можно изучать как движение прямолинейного отрезка в этой плоскости.
Перемещение фигуры можно осуществить совокупностью двух перемещений: поступательного и поворота.
Вариантов перемещений может быть столько, сколько точек плоской фигуры, т.е. бесчисленное множество.
Теорема. Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и вращательной скорости этой точки во вращательном движении фигуры вокруг полюса.
(Полюс- произвольная точка плоской фигуры, относительно которой поворачивается фигура)
Выполним построения как на рис. 8.2
За все время движения относительно О1 сохраняется зависимость
Следствие 1. Проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны.
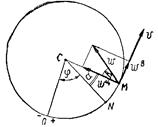
Пусть известна скорость uА точки А плоской фигуры, направление ее вращения и модуль угловой скорости w фигуры (Рис. 8.3).
Приняв точку А за полюс, определим скорости точек В и D плоской фигуры, лежащих на одной прямой с точкой А:
Причем вращательные скорости этих точек вокруг полюса А
uАВ= b1B1, uАD=d1D1 направлены перпендикулярно к отрезкам АВ и AD в сторону вращения фигуры.
Проведем ось х через точки A, D, В и спроектируем скорости этих точек на ось х; тогда
т.е. проекции скоростей всех точек отрезка АВ на ось х, направленную вдоль этого отрезка, равны между собой.
Следствие 2. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.
Пример 8.2 По заданной скорости одной точки плоской фигуры построить годограф возможных скоростей другой точки этой фигуры.
Решение. Проведем через А и В ось х и найдем проекцию Аа скорости uА на эту ось.
Из следствия 1 проекция скоростей точек А и В на эту ось равны. Отложим по оси х от точки В проекцию Вb,равную по величине проекции Аа и совпадающую с ней по направлению.
В точке b восставим перпендикуляр к оси х. Только на этой прямой и может находиться конец скорости uВ. Эта прямая является годографом возможных скоростей точки В.
8.4. План скоростей.
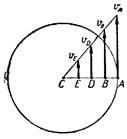
Зависимость между скоростями точек плоской фигуры (рис.8.5) позволяет определять скорости точек этой фигуры простым и наглядным построением, называемым планом скоростей.
Выполненное построение при известных скоростях точек A,B,C,D называется планом скоростей; отрезки Оа, Ob, Oc, Od называются лучами, а точки a, b, c, d вершинами плана скоростей.
Из треугольника aOb
Ob= Oa+ ab
Из сопоставления (а) и (б) устанавливаем, что ab= uАВ ; аналогично
Следовательно, каждый из отрезков, соединяющих вершины плана скоростей, геометрически равен вращательной скорости соответствующей точки вокруг другой точки как вокруг полюса.
и т.д. Отсюда следует, что многоугольник abcd подобен многоугольнику ABCD и повернут относительно последнего на 90° в сторону вращения движущейся плоской фигуры.
Для построения плана скоростей допустим, что известны модуль и направление скорости точки А (рис. 8.6) и прямая, по которой направлена скорость другой точки В фигуры.
Из произвольной точки О-полюса проведем отрезок Оа= uА и прямую, параллельную прямой, по которой направлена скорость uВ (рис.8.6). Известно, что отрезки, соединяющие вершины плана скоростей, перпендикулярны к отрезкам, соединяющим соответствующие фигуры.
Для получения вершины с плана скоростей следует провести из вершин a, b прямые, перпендикулярные к сторонам треугольника АС и ВС. Точка их пересечения и будет вершиной с, а отрезок Ос определит скорость точки с.
Аналогично можно определить скорость любой точки плоской фигуры, соединив ее с двумя точками, скорости которых уже известны.
Откладывая отрезки Оа, Ob и др., следует иметь ввиду, что их модуль равен соответствующей скорости в некотором соотношении. Например,
Вращение маховика в период пуска машины определяется уравнением фи=7t+0,8t^2. Определить модуль и направление ускорения точки лежащей на ободе маховика, в тот момент, когда ее скорость равна 3,4 м/с, а диаметр маховика 0,35 м.
Ответы 2
Закон изменения угловой скорости маховика
Закон изменения углового ускорения маховика
Угловое ускорение постоянно, следовательно вращение равноускоренное
R = 0.5 D = 0.5 · 0.35 = 0.175 (м)
Cкорость точки маховика
v(t) = ω(t) · R = 0.175 ω(t)
По условию в момент времени t₁
Угловая скорость в момент времени t₁
ω(t₁) = 3.4 : 0.175 ≈ 19.43 (рад/с)
Центростремительное ускорение точки в момент времени t₁

Касательное ускорение точки \

Модуль полного ускорения точки
Угол α между вектором полного ускорения точки и радиусом
Определение скорости и ускорения точки.
Ускорение точки – векторная величина, характеризующая быстроту изменения модуля и направления скорости точки.
Задание скорости и ускорения точки естественным способом
При задании точки естественным способом известен закон движения, выраженный зависимостью перемещения точки от времени
В этом случае скорость точки будет определяться как первая производная от данной зависимости
Ускорение точки будет определяться как вторая производная от зависимости перемещения или как первая производная от зависимости скорости
Точка движется по окружности радиусом R согласно уравнению.
Определить скорость и ускорение точки в конце 3 секунды

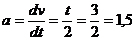
Задание скорости точки координатным способом
При задании точки координатным способом известны законы изменения координат данной точки в зависимости от времени 
В этом случае скорость точки будет определяться как геометрическая сумма первых производных от данных зависимостей

Ускорение точки будет определяться как геометрическая сумма первых производных от зависимостей скорости или вторых производных от зависимости изменения координат

Уравнения движения точки имеют вид
Определить уравнения скорости и ускорения данной точки
Если направление ускорения совпадает с направлением скорости (имеет одинаковый знак) то тело движется с положительным ускорением (ускоряется), если направление ускорения не совпадает с направлением скорости (имеет разные знаки) то тело движется с отрицательным ускорением (замедляется)
Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.
Все точки твердого тела, движущегося поступательно, описывают тождественные и параллельные между собой траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.
Для описания скорости и ускорения точки используются зависимости рассмотренные в предыдущем вопросе.
Вращательное движение
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.
Аналогом перемещения во вращательном движении является угол поворота 
Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростьютела.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорениемтела.
Рассмотрим движение точки М тела движущуюся по окружности с радиусом R.
Обозначим точку отсчета О, и угол, на который повернется эта точка за время t через 
За время t точка М пройдет расстояние s равное длине дуги окружности ОМ. Это расстояние определяется по формуле.
Скорость точки М в момент времени t при вращательном движении направлена по касательной к окружности в этой точке и называется окружной скоростью.
Величина окружной скорости определяется из выражения.
Из предыдущей формулы следует, что модули окружных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Ускорение точки М в момент времени t при вращательном движении складывается из двух составляющих вращательного ускорения (тангенциального) и центростремительного ускорения (нормального).
Тангенциальное ускорение направлено по касательной к окружности в точке М.
Величина тангенциального ускорения определяется по зависимости
Нормальное ускорение направлено по радиусу окружности к её центру.
Величина нормального ускорения определяется по зависимости
Полное ускорение точки определится из выражения
Вращение маховика в период пуска машины определяется уравнением
По уравнению вращения маховика находим его угловые скорость и ускорение
Определяем уравнение окружной скорости точки
Выражаем отсюда время

Тангенциальное ускорение 
Нормальное ускорение 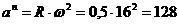
Полное ускорение 
Вращательное движение
Вращательным называется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения.
При этом движении все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси.
Аналогом перемещения во вращательном движении является угол поворота 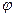
Величина, характеризующая быстроту изменения угла поворота с течением времени, называется угловой скоростьютела.
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорениемтела.
Рассмотрим движение точки М тела движущуюся по окружности с радиусом R.
Обозначим точку отсчета О, и угол, на который повернется эта точка за время t через 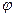
За время t точка М пройдет расстояние s равное длине дуги окружности ОМ. Это расстояние определяется по формуле.
Скорость точки М в момент времени t при вращательном движении направлена по касательной к окружности в этой точке и называется окружной скоростью.
Величина окружной скорости определяется из выражения.
Из предыдущей формулы следует, что модули окружных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.
Ускорение точки М в момент времени t при вращательном движении складывается из двух составляющих вращательного ускорения (тангенциального) и центростремительного ускорения (нормального).
Тангенциальное ускорение направлено по касательной к окружности в точке М.
Величина тангенциального ускорения определяется по зависимости
Нормальное ускорение направлено по радиусу окружности к её центру.
Величина нормального ускорения определяется по зависимости
Полное ускорение точки определится из выражения
Вращение маховика в период пуска машины определяется уравнением
По уравнению вращения маховика находим его угловые скорость и ускорение
Определяем уравнение окружной скорости точки
Выражаем отсюда время
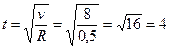
Тангенциальное ускорение 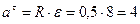
Нормальное ускорение 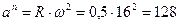
Полное ускорение 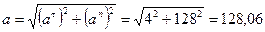
Вращение маховика в период пуска машины определяется уравнением фи=7t+0,8t^2. Определить модуль и направление ускорения точки лежащей на ободе маховика, в тот момент, когда ее скорость равна 3,4 м/с, а диаметр маховика 0,35 м.
Ответы 2
Закон изменения угловой скорости маховика
Закон изменения углового ускорения маховика
Угловое ускорение постоянно, следовательно вращение равноускоренное
R = 0.5 D = 0.5 · 0.35 = 0.175 (м)
Cкорость точки маховика
v(t) = ω(t) · R = 0.175 ω(t)
По условию в момент времени t₁
Угловая скорость в момент времени t₁
ω(t₁) = 3.4 : 0.175 ≈ 19.43 (рад/с)
Центростремительное ускорение точки в момент времени t₁

Касательное ускорение точки \

Модуль полного ускорения точки
Угол α между вектором полного ускорения точки и радиусом