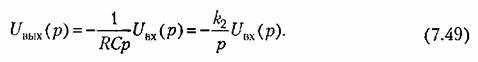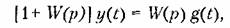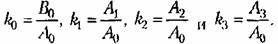Вычислительная машина график использования слова
Использование вычислительных машин
За последнее время для исследования систем автоматического управления и, в частности, для построения переходных процессов стали широко применяться вычислительные машины непрерывного действия и цифровые вычислительные машины. Удобство первых заключается в том, что физическому процессу, протекающему в исследуемой системе, соответствует протекание в вычислительной машине (модели) некоторого другого аналогового процесса, описываемого теми же диффереициальными уравнениями, что и исходный процесс. Это позволяет изучать процессы в системах управления наиболее наглядно, так как каждый обобщенной координате в исследуемой системе соответствует некоторая переменная в вычислительной машине, например электрическое напряжение.
Моделирующие или аналоговые вычислительные машины позволяют моделировать как всю систему в целом, так и отдельные ее части. Так, например, часто вычислительная машина используется для моделирования объекта, например самолета, корабля, паровой турбины, двигателя внутреннего сгорания и т. п., а само управляющее устройство может быть реальным. При сопряжении реального управляющего устройства с объектом, в качестве которого выступает модель, получается замкнутая система, которая может быть исследована еще до того, как будет построен сам объект.
Вычислительные машины целесообразно использовать для исследования обыкновенных линейных систем в тех случаях, когда последние описываются дифференциальными уравнениями сравнительно высокого порядка и их аналитическое исследование становится малоэффективным. Однако наибольшее значение имеют вычислительные машины при исследовании линейных систем с переменными параметрами и нелинейных систем, поскольку для этих случаев пока еще мало разработано приемлемых для практики методов, а иногда аналитические методы вообще отсутствуют.
Точность моделирующих вычислительных машин обычно не превосходит нескольких процентов. В большинстве случаев этого оказывается достаточно для целей практики. Получение точности в десятые доли процента и выше связано со значительным увеличением стоимости машин. В этом отношении целесообразнее использовать цифровые вычислительные машины, которые сравнительно просто могут обеспечить высокую точность вычислений.
Следует заметить, что моделирование не призвано полностью заменить аналитические методы исследования систем. Комплекс технических задач, связанных с проектированием, конструированием, регулировкой и настройкой систем, весьма сложен, и он всегда должен опираться па сознательные расчетно-теоретические методы. Моделирование же процессов на вычислительных машинах во многом сводится к просматриванию некоторого количества возможных вариантов, разобраться в которых, а также наметить их предварительно можно при помощи существующих теоретических методов анализа и синтеза. Наилучшим решением в настоящее время является взаимная увязка расчетно-теоретических методов и методов моделирования, так как они взаимно дополняют друг друга и позволяют наиболее полно и быстро решить задачу разработки сложной системы управления.
Электронные модели. Электронные моделирующие вычислительные машины имеют наибольшее применение вследствие их сравнительной простоты в изготовлении и эксплуатации. Процессы в исследуемой системе изучаются при помощи наблюдения процессов в некоторой электронной схеме, которая описывается теми же дифференциальными уравнениями, что и исходная система.
Пусть исследуемая реальная система описывается совокупностью уравнений, разрешенных относительно первых производных
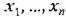
В электронной модели должна быть реализована совокупность дифференциальных уравнений аналогичного вида:


При выборе масштаба времени должно учитываться то обстоятельство, что электронные модели могут точно работать при ограниченном времени протекания моделируемого процесса. Это время не должно обычно превышать нескольких сотен секунд, что связано с особенностями работы электронных интеграторов.

Существует две разновидности электронных моделирующих машин: модели структурного типа и модели матричного типа. Первые позволяют моделировать структурную схему системы, что во многих случаях оказывается более удобным и наглядным.
Модели матричного типа требуют записи дифференциальных уравнений исследуемой системы в особой, матричной форме. Матричные модели менее удобны для исследования систем и потому используются реже.
Остановимся вначале па имеющих наибольшее применение моделях структурного типа. Они построены на базе так называемых операционных усилителей, выполняющих операции интегрирования, суммирования и умножения на постоянный множитель.
Операционный усилитель представляет собой усилитель постоянного тока с большим коэффициентом усиления по напряжению (десятки и сотни тысяч). Динамические свойства усилителя таковы, что он может быть замкнут 100%-ной отрицательной обратной связью через резистор или конденсатор без потери устойчивости (без генерации) в замкнутом состоянии.
Передаточная функция усилителя, замкнутого обратной связью (рис. 7.3) при большом коэффициенте усиления может быть достаточно точно представлена в виде


Знак минус в формуле (7.47) показывает, что операционный усилитель инвертирует входной сигнал (меняет его знак). Современные усилители обычно имеют как инвертирующий, так и неинвертирующий входы.
Рассмотрим три основных режима работы усилителя.
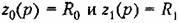
Упрощенное изображение такого усилителя показано на рис. 7.4, а справа.
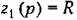
Два варианта упрощенного изображения такого усилителя изображены на рис. 7.4, б справа.

Упрощенное изображение такого усилителя показано на рис. 7.4, в справа. Режим дифференцирования обычно не используют при моделировании, так как в этом режиме сильно возрастает влияние высокочастотных помех и наводок.
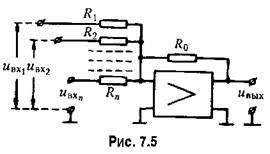
В табл. 7.3 приведены типичные случаи использования операционного усилителя для получения различных динамических звеньев.
В таблице использован машинный оператор дифференцирования
Электронная модель структурного типа имеет в своем составе несколько операционных усилителей, которые могут работать в режиме интегрирования, т. е. с конденсатором в цепи обратной связи. Число этих усилителей определяет наивысший
порядок дифференциального уравнения, которое может быть исследовано на данной модели. Кроме того, имеется ряд вспомогательных усилителей, при помощи которых можно осуществлять операции умножения на постоянный множитель (масштабирование), перемены знака (инвертирование) и суммирования.
Исследуемые процессы в виде изменения машинных переменных (напряжений) могут наблюдаться и фиксироваться при помощи осциллографов и графопостроителей.
Для приложения к электронной модели исследуемой системы задающих и возмущающих воздействий используются генераторы, которые могут воспроизводить требуемые функции времени, например линейную функцию, синусоиду, экспоненту, прямоугольную или треугольную волну и т. п., в виде соответствующего изменения электрического напряжения. Существуют также генераторы случайных величии.
Кроме того, электронная модель имеет ряд вспомогательных устройств, позволяющих после набора исследуемой задачи производить пуск и остановку решения дифференциальных уравнений, фиксацию решения в заданной точке, периодизацию решения и т. п.
Набор задачи на электронной модели структурного типа может быть осуществлен двумя способами:
по дифференциальному уравнению, которым описывается исследуемая система;
по структурной схеме исследуемой системы.
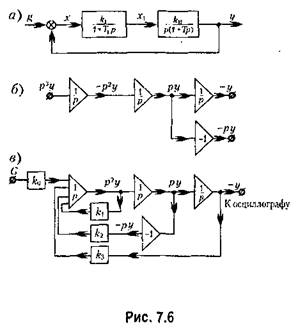
Рассмотрим порядок набора задачи на простейшем примере. Начнем с первого способа. Пусть дана система, структурная схема которой представлена на рис. 7.6, а. Для этой схемы передаточная функция разомкнутой системы
Дифференциальное уравнение замкнутой системы, записанное в символической форме, в соответствии с гл. 5 будет

В рассматриваемом случае, учитывая (7.53), получим


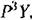
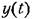
Второй способ набора задачи на электронной модели заключается в том, что воспроизводится структурная схема, изображенная на рис, 7.6, а. Звено второго порядка удобнее представить в виде последовательно включенных звеньев первого порядка, каждое из которых может быть реализовано на базе одного интегратора. Это представлено на рис, 7.7, а. Схема набора, построенная в соответствии с табл. 7.3, изображена на рис. 7.7, б.
Для уяснения методики подсчета коэффициентов рассмотрим, например, второе звено (рис. 7.7). Исходная передаточная функция имеет вид
Это уравнение и набрано на втором интеграторе (рис. 7.7, б). Передаточные коэффициенты усилителя но соответствующим входам определяются из (7.59):
Аналогичным образом составляется схема набора остальных звеньев, входящих в структурную схему (рис. 7,7;а).
Получившаяся схема набора (рис. 7.7, б) представляет собой совокупность операционных усилителей в режиме интегрирования, замкнутых местными отрицательными обратными связями.
По сравнению с моделированием дифференциального уравнения (рис. 7.6) моделирование структурной схемы имеет преимущество в смысле большего соответствия модели исследуемой системе. Кроме того, моделирование структурной схемы позволяет просто учитывать при исследовании системы типичные нелинейности, например ограничение переменной величины, зону нечувствительности, релейную характеристику, люфт и т. н. Эти характеристики могут быть реализованы в электронной
модели посредством использования диодных элементов. В табл. 7.4 приведены некоторые типичные нелинейности и электронные схемы с диодными элементами, позволяющие реализовать в модели эти характеристики. Кроме этих простейших нелинейных блоков в электронных моделях применяются более сложные схемы, позволяющие реализовать различные криволинейные характеристики, операции возведения в степень и извлечения корня, операции перемножения двух переменных И Т. II.
На рис. 7.8 для иллюстрации приведена структурная
схема нелинейнойхледящей системы (рис. 7.8, а) и схема набора на электронной модели (рис. 7.8, б, Схема набора на рис. 7.8, б изображена несколько подробнее по сравнению со схемами на рис. 7.6 и 7.7.
Все, что было рассмотрено выше, относится к моделированию линейных-дифференциальных уравнений с постоянными коэффициентами. При необходимости исследовать процессы в системах с переменными коэффициентами или в системах с временным запаздыванием к линейной электронной модели добавляются соответственно блоки переменных коэффициентов и блоки временного запаздывания. Добавление нелинейных блоков позволяет исследовать процессы в нелинейных системах. Все эти добавочные блоки существенно повышают эффективность электронных моделей, так как позволяют сравнительно просто и достаточно точно исследовать процессы в сложных системах, что является в большинстве случаев недоступным для аналитических методов расчета.
Цифровые вычислительные машины
В вычислительных машинах непрерывного действия достижимая точность ограничивается точностью изготовления входящих в машину элементов. Повышение точности всегда связано со значительным удорожанием изготовления, а в некоторых случаях желаемая точность вообще не может быть достигнута при современном уровне техники. В цифровых вычислительных машинах принципиально может быть достигнута любая желаемая точность вычислений. Это связано лишь с увеличением числа используемых разрядов в изображении чисел, что вызывает умеренный рост стоимости вычислительных машин при росте их точности.
Цифровые вычислительные машины по своему принципу действия относятся к устройствам дискретного действия. Результаты вычислений выдаются этими машинами не непрерывно, а в виде последовательности дискретных чисел. Цифровые вычислительные машины могут применяться для различных целей. В том числе их можно использовать для решения линейных и нелинейных дифференциальных уравнений с постоянными и переменными коэффициентами, что нужно для исследования процессов в сложных системах управления.
Любые вычисления, которые производит цифровая вычислительная машина, сводятся к последовательности арифметических и логических операций. Это означает, что решение дифференциальных уравнений исследуемой системы осуществляется методами численного интегрирования по шагам и точность получаемого решения будет зависеть от величины выбранного шага интегрирования.
В настоящее время разработано большое количество разнообразных алгоритмических языков, которые значительно облегчают вопросы программирования, и множество стандартных программ для решения линейных и нелинейных дифференциальных уравнений. Современные оконечные устройства цифровых вычислительных машин позволяют получать решения как в виде таблиц, так и в виде готовых графиков.
К числу недостатков цифровых вычислительных машин следует отнести трудности сопряжения с реальной аппаратурой.
Электронно-вычислительная машина
Согласно Большому энциклопедическому словарю,2000 ЭВМ — то же, что компьютер.
Задолго до появления ЭВМ существовали другие виды вычислительных машин.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Существуют и иные значения этого слова, см. Мир«МИР» (сокращение от «Машина для Инженерных Расчётов») — серия электронных вычислительных машин, созданных Институтом кибернетики Академии наук Украины, под руководством академика В. М. Глушкова.
Необходимость разделять вычислительные задачи и выполнять их одновременно (параллельно) возникла задолго до появления первых вычислительных машин.
Вычислительная техника является важнейшим компонентом процесса вычислений и обработки данных. Первыми приспособлениями для вычислений были, вероятно, всем известные счётные палочки, которые и сегодня используются в начальных классах многих школ для обучения счёту. Развиваясь, эти приспособления становились более сложными, например, такими как финикийские глиняные фигурки, также предназначаемые для наглядного представления количества считаемых предметов. Такими приспособлениями, похоже, пользовались.
Интегра́льная (микро)схе́ма (ИС, ИМС, IC (англ.)), микросхе́ма, м/сх, чип (англ. chip «тонкая пластинка»: первоначально термин относился к пластинке кристалла микросхемы) — микроэлектронное устройство — электронная схема произвольной сложности (кристалл), изготовленная на полупроводниковой подложке (пластине или плёнке) и помещённая в неразборный корпус или без такового, в случае вхождения в состав микросборки.
Система числового программного управления (СЧПУ) «Электроника НЦ-31» — это система контурного управления типа ЧПУ. Она предназначена для оперативного управления станками со следящими электроприводами по двум линейным осям, главным приводом и измерительными фотоимпульсными датчиками. Система позволяет создавать мультипроцессорные конфигурации (до четырёх процессоров), стандартная корзина позволяет использовать два процессора, но во всех станочных применениях используется однопроцессорная конфигурация.
Вычислительная машина
Вычислительная машина, счётная машина — механизм, электромеханическое или электронное устройство, предназначенное для автоматического выполнения математических операций.
В последнее время, это понятие чаще всего ассоциируется с различными видами компьютерных систем. Тем не менее, вычислительные механизмы появились задолго до того, как заработал первый компьютер.
Ещё в 1623 году немец Вильгельм Шиккард (нем. Wilhelm Schickard ) создал так называемые «Считающие часы», которые сегодня принято считать первым автоматическим калькулятором. В письмах к Иоганну Кеплеру Шикард объяснял, как можно использовать его машину для расчёта астрономических таблиц. Машина Шикарда умела складывать и вычитать шестизначные числа, оповещая звонком о переполнении. Более сложные вычисления выполнялись с помощью набора костяшек Непера, установленного на корпусе механизма. Оригинал машины был потерян при пожаре ещё до начала двадцатого столетия. В 1960 году на основе сохранившихся чертежей была построена копия этого вычислителя, подтвердившая его существование и работоспособность.
В 1642 году машину, помогающую в сложении чисел изобрёл французский учёный Блез Паскаль. «Паскалина», как назвал свою конструкцию изобретатель, представляла собой механическое устройство в виде ящичка, наполненного многочисленными шестерёнками. Складываемые числа вводились в машину за счёт соответствующего поворота наборных колёсиков. На каждом из этих колёсиков, соответствовавших одному десятичному разряду, были нанесены деления с цифрами от 0 до 9. При вводе числа колёсики прокручивались до соответствующей цифры. При завершении полного оборота избыток над цифрой 9 переносился на соседний разряд (на 1 позицию сдвигалось соседнее колесо) и так далее. «Машина Паскаля» позволяла выполнять не только сложение, но и другие операции, однако при этом требовала применения довольно неудобной процедуры повторных сложений.
В 1673 году другой известный учёный — Готфрид Вильгельм Лейбниц изготовил механический калькулятор, позволявший легко выполнять вычитание, умножение и деление.
1723 год — немецкий математик и астроном Христиан Людвиг Герстен на основе работ Лейбница создал арифметическую машину. Машина высчитывала частное и произведение (за счёт последовательно выполняемых операций сложения). Кроме того, в ней была предусмотрена возможность контроля за правильностью ввода данных.
В 1820 году француз Тома де Кальмар наладил промышленный выпуск арифмометров.
Разработанная в 1823 году разностная машина англичанина Чарльза Бэббиджа предназначалась для расчётов математических таблиц.
Изучение работ Бэббиджа и его советы помогли шведскому изобретателю Перу Георгу Шойцу (швед. Georg Scheutz ), начиная с 1854 года, построить несколько разностных машин, а в 1859 году даже продать одну из них канцелярии английского правительства.
Ещё одна «Разностная машина», построенная вскоре Мартином Вибергом (швед. Martin Wiberg ), также была в своей основе улучшенной версией машины Чарльза Бэббиджа и использовалась для расчёта и публикации печатных логарифмических таблиц.
К 1890 году американцем Германом Холлеритом была разработана электрическая табулирующая система, которая использовалась в переписях населения США в 1890 и 1900 годах.
В 1938 году немецкий инженер Конрад Цузе на квартире родителей построил свою первую машину, названную Z1. Это была пробная модель полностью механической программируемой цифровой вычислительной машины. В том же году Цузе приступил к созданию машины Z2. А в 1941 году Цузе создаёт первую вычислительную машину, обладающую всеми свойствами современного компьютера Z3.
Вычислительные машины
Вычислительные машины, являются неотъемлемой частью современной жизни. В повседневной жизни человек ежесекундно сталкивается с разного рода вычислениями или результатом таковых.
В процессе своего развития вычислительная техника прошла долгий путь эволюции от простейших палочек для вычисления до машин, способных выполнить любое математическое действие в тысячные доли секунды.
Самым простым примером продвинутой вычислительной машины, является компьютер, который постоянно принимает, обрабатывает и передает данные. Весь текст и картинки, которые видны на экране для компьютера, выглядят как бинарный код из «1» и «0».
В зависимости от порядка расположения «1» и «0» вычислительная машина выводит на экран тот или иной символ.
История развития вычислительных машин
История развития вычислительных машин начала еще в древние времена, когда для выполнения простейших вычислительных операций, человек использовал средства для визуализации счета.
Первыми известными приспособлениями для вычисления являются счетные палочки. Далее, в процессе эволюции счетные палочки изменили свой внешний вид. Например, во многих религиях для отсчета количества прочитанных молитв стали применять четки.
Не так давно, на одном из античных судов было найдено устройство, которое могло выполнять простые математические операции. Главной особенностью этой находки, являлось назначение устройства: механизм был создан для вычисления лунных фаз и, скорее всего, использовались как календарь.
Ученые пришли к выводу, что технология производства такой машины была утеряна, и более человеку не удавалось создать подобного аппарата вплоть до эпохи процветания.
Греческие купцы, имели при себе специальные таблички, на которых была изображена своеобразная система подсчета, отдаленно напоминающую современную таблицу умножения.
Для определения качественных характеристик таких, как килограммы, для подсчета использовались простые весы. Процесс вычислений заключался в следующем: прибор оценивал вес изделия, переводя его в числовое значение.
Процесс эволюции систем для счета происходил в следующей хронологии:
Разработка вычислительных машин не стоит на месте. Ученые говорят о скором появлении оптического или фотонного вычислителя, который сможет работать в 1000 раз быстрее, чем обыкновенный компьютер.
Первые механические вычислительные машины
Главное отличие механической вычислительной техники от современной заключается в использовании при вычислениях механической силы. В механических приборах алгоритмы запускались при помощи шестерней и рычагов, и требовали ручного ввода информации.
Долгий путь эволюции такой вычислительной техники отмечен созданием двух наиболее продвинутых аппаратов Паскаля и Бэббиджа. Эти механические вычислительные машины разработаны в разные времена и использовали прогрессивные методы подсчета чисел.
Вычислительная машина Бэббиджа
Машина Бэббиджа – это универсальный вычислительный прибор, который так и не был создан. До нашего времени дошли чертежи этой машины, на основе которой современные ученые собрали прототип машины и доказали, что разработка была удачной.
Английский математик Чарльз Бэббидж при создании своей машины опирался на труды предшественников 18 века. Основополагающими трактатами для разработки проекта стала работа немецкого ученого Иоганна Мюллера. Книга о механических вычислениях, изданная в 1788 году и труды Гаспара де Порни по созданию иерархической структуры для организации массовых вычислений.
Разностная машина, которая впервые была описана Бэббиджем в 1822 году в своей книге, могла считать значения многочленов до шестой степени. В том же 1822 году, ученый приступил к созданию своего аппарата, сразу по старту проекта, который спонсировало правительство, начались трудности.
Механические вычисления, требовали высочайшей точности в производстве деталей. Небольшие отклонения в расчетах могло привести к высокой погрешности в результате.
Подрядчик, который взялся изготавливать оборудование и запчасти для вычислительной машины, не смог выполнить детали с необходимой точностью. Поэтому машина так и не была собрана, а финансирование проекта в скором времени прекратилось. По оставшимся документам, вычислительный механизм собрали уже в конце 20 века.
Вычислительная машина Паскаля
Ученый Блэз Паскаль вырос в семье французского сборщика налогов. Главной мотивацией для создания суммирующей машины, стало стремление облегчить процесс подсчета налогов. В 1642 году Паскаль занялся разработкой методов и алгоритмов работы будущего устройства.
Счетная машина, которую ученый назвал «Паскалита», представляла собой ящик с наборными колесами. Путем вращения колес вводилось необходимое число, а в верхней части в специальных «окошках», пользователь мог увидеть сумму введенных чисел.
Первоначально, машина могла считать в пределах четырехзначных чисел. В процессе усовершенствования, машина снабдили 8 оконцами, что позволило вести вычисления для более крупных чисел и сложных выражений.
Несмотря на успех, который принесла Паскалю его суммирующая машина, больших объемов продаж добиться не удалось. Это было связано с высокой стоимостью запчастей и сложностями производства.
Хотя именно принцип передачи информации в машине, путем движения связанных между собой колес, более трех веков использовался в производстве и разработке счетных машин по всему миру. Машина Паскаля, была одной из первых реально работающих образцов механической вычислительной техники.
Классификация вычислительных машин
Все вычислительные машины можно разделить на три одинаковые группы, различия которых заключается в методах исчисления данных и способах обработки.
Вычислительные комплексы, системы и сети
К вычислительным комплексам, системам и сетям, относится группа вычислительной техники, которая работает в одном направлении и обеспечивает расчет необходимых величин по данным из нескольких источников. Самым обычным примером вычислительной сети – является компьютерная сеть. Как правило, такие группы оборудования применяются в промышленности, для достижения оптимизации вычислений.
Механические вычислительные машины
В современном виде вычислительные механические машины – это довольно сложное и точное оборудование. Самой распространенной формой механических вычислительных машин являются разнообразные счетчики.
Цифровые вычислительные машины
В цифровых вычислительных машинах, алгоритм расчетов производится, благодаря поступлению определенных дискретных значений, которые в свою очередь после подсчета выводятся на экран в виде цифрового значения.
Большинство ЦВМ используют импульсы или специальный, общепринятый двоичный код. Это сделано, для того чтобы вычислительные комплексы и системы, могли обмениваться между собой информацией «понятной» для всех машин.
Аналоговые вычислительные машины
Главным отличием аналоговой машины от цифровой или механической является беспрерывность действий по обработке данных. При этом вычисления могут вести за собой какое-то механическое, гидравлическое или электронное действие.
Самым ярким примером, является автоматическая коробка передач у автомобиля, которая постоянно получает данные о режимах работы двигателя и соответственно произведенным расчетам переключает скорости.
Электромеханические вычислительные машины
История первых электромеханических машин, начинается вместе с созданием нового электронного элемента – реле. Ведущие разработчики, сразу оценили возможность переделывать механическое движение в определенный электрический код при помощи реле.
Сразу несколько групп инженеров начали заниматься такими машинами в тридцатых годах двадцатого века. В это время развитие электроники пошло быстрее и разработку электромеханических счетных машин быстро закрыли. За неполные 7 лет разработок, на основе релейного действия, было создано две машины – «Марк 1» и «Марк 2».
На современном производстве применение электромеханических машин сведено к минимуму из-за появления более продвинутого оборудования.
Релейные вычислительные машины
После того как электрические реле стали набирать популярность, было создано несколько машин, которые при помощи механической силы могли вести определенные вычисления. Через некоторое время механическую силу полностью заменили силой тока, которая и питала релейную установку.
Первая удачная и надежная машина – РВМ-1 (Релейно вычислительная машина) была создана в 1957 году. Устройство использовало в работе одновременно 550 реле. Скорость подсчета такой машины была 0,5 секунд на выполнение одной операции, при этом устройство могло работать постоянно – без остановок.
РВМ-1 применялась на протяжении 10 лет в финансовой системе. Последний раз на территории нашей страны ее запускали для пересчета финансовой системы СССР в 1967 году. Именно тогда была зафиксирована самая большая нагрузка, и за одну секунду машина смогла выполнить до 20 операций умножения крупных чисел.
Простые вычислительные машины
Примером простых вычислительных машин является самый простой калькулятор. Первые машины этого вида начали выпускаться во второй половине 20-го века. Простая вычислительная машина нуждается в помощи оператора, задачей которого является ввод цифр. Пик развития таких машин пришелся на восьмидесятые года 20 века, а их вид практически не изменился.
Простые вычислительные машины, рассчитаны на обработку таких действий, как:
Упоминание единичных простых машин, можно встретить и в более раннем периоде. Но тогда большой популярностью простые вычислительные машины не пользовались из-за высоких требований к знаниям оператора машины и большой себестоимостью.
Производители и поставщики вычислительных машин
Современные вычислительные машины, в 90% случаев являются персональными компьютерами, на которых установлены специальные программы, позволяющие выполнять необходимые вычисления мгновенно.
Среди представителей этой индустрии можно отметить компании: «НИКС», DNS, Meijin, «МЦСТ», «Т-Платформы» и другие.
Мировыми лидерами являются компании Intel и Kingston. Серверное оборудование является большой вычислительной машиной, которая постоянно обрабатывает и передает данные.
Крупным производителем серверов является компания Dell. На продукции этой компании в мире работает около 23% серверов различного профиля и назначения.
Поставками вычислительной техники занимаются крупные торговые сети, специализирующиеся на компьютерном обеспечении. Заказ партии вычислительных машин можно сделать по интернету или в самом магазине. Некоторые из этих компаний имеют собственные производства по сборке оборудования. Среди поставщиков можно выделить сеть магазинов «Кей», «Ситилинк», «Юлмарт».
Больше о производителях и поставщиках вычислительных машин можно узнать на ежегодной выставке «Связь».