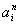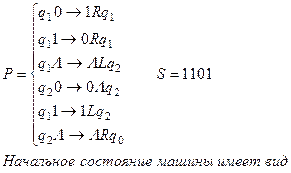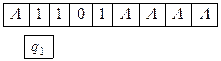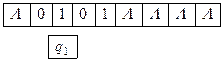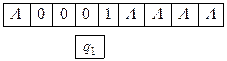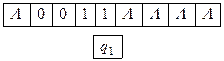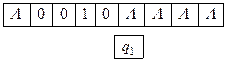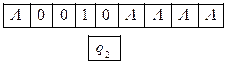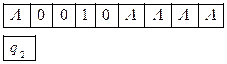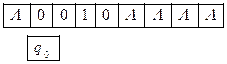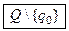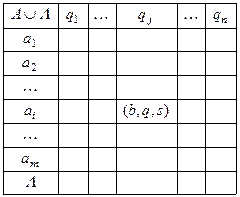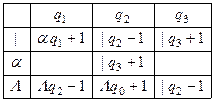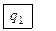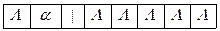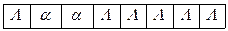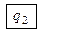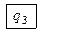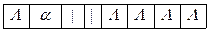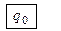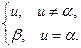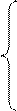Выяснить применима ли машина тьюринга заданная программой p к слову s

Выяснить, применима ли машина Тьюринга T к слову P

Помогите решить задачу.
Выяснить, применима ли машина Тьюринга T к слову P. Если применима, то выписать результат T(P) применения машины Тьюринга T к слову P.

q1 1 q2 1 E
q2 1 q3 1 E
q2 0 q2 1 L
q3 1 q1 0 R
q3 0 q2 0 R

Предполагается, что начальный момент машины Тьюринга обозревает самую левую единицу слова.

q1 11001101
q2 11001101
q3 11001101
0 q1 1001101
0 q2 1001101
0 q3 1001101
00 q2 001101

Выяснить, применима ли машина Тьюринга, заданная программой Р к слову S и, если применима, то указать результат
Выяснить, применима ли машина Тьюринга, заданная программой Р к слову S и, если применима, то.

Выяснить, применима ли машина Тьюринга T к слову P?
Почему мой ответ неверен? Выяснить, применима ли машина Тьюринга T к слову P. Если применима, то.

Выяснить, применима ли машина Тьюринга T к слову P
Добрый день. Прошу помочь в решение задачи и расписать по возможности подробно. Выяснить.

Подобная задачка. Подскажите правильно ли я понял:

q1 1 q3 0 E
q1 0 q2 1 E
q2 1 q1 0 L
q3 1 q2 1 L
q3 0 q1 1 R

МТ обозревает самую левую единицу слова

Мне не понятна часть с q3 =1, получается такого состояния вообще быть не может.

Объясните пожалуйста, в чем загвоздка.

Выяснить, применима ли машина Тьюринга, заданная программой Р, к слову S
Что-то очень подозрительное с Машиной Тьюринга Здравствуйте! Нужно решить задачу, но не могу.

Правила, когда применима машина Тьюринга к слову
Возник вопрос, применима ли машина Тьюринга к слову, если выполнение не останавливается? она в двух.

Применима ли машина Тьюринга?
Выяснить, применима ли машина Тьюринга, заданная программой P к слову S, и если применима, то.

Источник

Тема 9 Элементы теории алгоритмов

9.1 Машины Тьюринга

9.2 Рекуррентные функции

9.3 Тезисы Тьюринга и Чёрча

Понятие алгоритма стихийно формировалось с древнейших времен. Современный человек понимает под алгоритмом четкую систему инструкций о выполнении в определенном порядке некоторых действий для решения всех задач какого-то данного класса.

Многочисленные и разнообразные алгоритмы окружают нас буквально во всех сферах жизни и деятельности.

Большое количество алгоритмов встречаются при изучении математики буквально с первых классов школы. Это, прежде всего, алгоритмы выполнения четырех арифметических действий над различными числами – натуральными, целыми, дробными, комплексными. Примерами известных алгоритмов являются алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел, вычисление определителей различных порядков, вычисление рангов матриц с рациональными элементами, приближенное вычисление корней уравнений и т. д.

В начале ХХ века у математиков начали возникать подозрения в том, что некоторые массовые задачи, по-видимому, не имеют алгоритмического решения. Для точного доказательства несуществования алгоритма необходимо иметь его точное математическое определение. Первые работы по уточнению понятия алгоритма и его изучению были выполнены в 1936–1937 гг. А. Тьюрингом, Э. Постом, К. Геделем, А. А. Марковым, А. Черчем. Было выработано несколько определений понятия алгоритма, но впоследствии выяснилось, что все они равносильны между собой, то есть определяют одно и то же понятие.

9.1 Машины Тьюринга. Машины Тьюринга есть математическая (вообразимая) машина, а не машина физическая. Она есть такой же математический объект, как функция, производная, интеграл и т. д. А так же, как и другие математические понятия, понятие машина Тьюринга отражает объективную реальность, моделирует некие реальные процессы.

Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки.

Лента разбита на ячейки. Во всякой ячейки в каждый момент времени находится в точности один символ из внешнего алфавита А=<а0,а1,…аn-1 >, n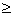2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой. В дальнейшем в качестве внешнего алфавита будем использовать А=<0,1>, где в качестве пустого символа будем использовать 0(нуль). В каждый момент времени лента содержит конечное число ячеек, но в процессе работы машины можно пристраивать новые ячейки в пустом состоянии.

Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита.

Работа машины Тьюринга определяется программой. Программа состоит из команд. Каждая команда представляет собой выражение одного из следующего вида:

Команда 1 заключается в том, что содержимое aj обозреваемой на ленте ячейки стирается, а на его места дописывается символ ae (который может совпадать с aj ), машина переходит в новое состояние qk (оно может совпадать с предыдущим состоянием qi ).

Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.

Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку.

Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии.

Машинным словом или конфигурацией называется слово вида

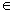
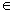
Где аijА, qkQ. Символ qk пишется перед символом обозреваемой ячейки. Причем символ qk может быть самым левым, но не может быть самым правым. В дальнейшем будем использовать следующие обозначение аin обозначает слово аi аi …аi =

Например, конфигурация 13q10212 на ленте выглядит следующим образом:

Источник

Машина Тьюринга.

Дата добавления: 2015-07-23 ; просмотров: 3457 ; Нарушение авторских прав

Работа алгоритма производится на некотором устройстве реализации, содержащем процессор для выполнения операций, внешнюю и внутреннюю память для хранения, поиска и изменения данных.

Одним из методов представления алгоритмов является машина Тьюринга (МТ), которая включает в себя следующие элементы.

Бесконечную в обе стороны ленту, разделенную на ячейки В каждой ячейке может быть записан один из символов рабочего алфавита машины 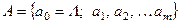.Любой алфавит должен содержать пустой символa₀ = Λ

а) если правая часть этой команды равна br, то М записывает в обозреваемую ячейку b, и УУ переходит в состояние r;

b) если правая часть этой команды равна bRr или bLr, то М записывает в обозреваемую ячейку b, головка сдвигается на одну ячейку вправо или влево соответственно, и УУ переходит в состояние r.

Формально, машина Тьюринга – это тройка М = (А, Q, P), где:

А – алфавит машины (т.е. символы, которые записываются в ячейки, включая пустой символ а₀ = Λ);

Q – конечное множество состояний УУ, содержащее два выделенных элемента q₁ и q₀;

Р – множество команд УУ, которое называется программой машины.

Если машина, начав работу с исходным словом, на некотором шаге придет в заключительное состояние, то она называется применимой к этому слову, а полученное слово результатом применения машины Тьюринга к исходному слову. Если же машина ни в какой момент времени не придет в заключительное состояние, то она называется неприменимой к данному слову, и результат ее работы неопределенен.

где верхняя строка – это записанное на ленте слово, нижняя строка показывает, какая в данный момент ячейка обозревается, и в каком состоянии находится УУ.

Найдем результат применения машины к слову S.

В начальный момент, как видно из таблицы, СЗУ обозревает символ 1 и УУ находится в состоянии q₁. Находим в программе команду с левой частью q₁1. Это команда 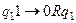Она означает, что в рассматриваемую ячейку записывается 0, головка сдвигается на одну ячейку вправо, и УУ устанавливается в состояние q₁. В результате применения этой команды имеем:

В этот раз обозревается символ 0 и УУ находится в состоянии q₁. Соответствующая команда в программе имеет вид q₁0 → 1Rq₁, поэтому в обозреваемую ячейку записывается 1, головка сдвигается на одну ячейку вправо, и УУ остается в состоянии q₁.

На следующем шаге обозревается символ 1 и УУ находится в состоянии q₁. выполняется команда

Далее обозревается пустая ячейка Λ, и УУ находится в состоянии q₁. Соответствующая команда имеет вид q₁Λ → ΛLq₂:

Далее, согласно программе, головка движется влево вдоль всего слова, не изменяя записанные в ячейках символы до тех пор, пока не примет следующее положение

В этом случае соответствующая команда имеет вид q₂Λ → ΛRq₀. Это означает, что обозреваемая ячейка остается пустой, головка сдвигается вправо и переходит в состояние q₀.

Состояние q₀ – заключительное, поэтому машина заканчивает работу, т.е. машина применима к слову S. Чтобы узнать результат применения, рассмотрим непустые символы на ленте, которые мы получили. Увидим, что слово S преобразовано в слово S′ = 0010.

Заметим, что данная программа реализует процесс инвертирования заданного слова т.е. замену единиц на нули, а нулей на единицы. Программа составлена таким образом, что в заключительном состоянии СЗУ обозревает первый символ полученного слова, т.е. возвращается в исходное положение.

Программу машины можно задать таблично.

Построить машину Тьюринга, удваивающую натуральные числа, записанные в унарной системе счисления.

Расширим исходный алфавит А = < | >до А′ =< |, α >. искомую машину построим в алфавите А′ 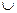<Λ>. Программа машины будет выглядеть так

При работе машина считывает букву в обозреваемой ячейке и находит клетку в таблице, соответствующую считанной букве (|, α, Λ) и состоянию машины (q_i ). ± сдвиг головки соответственно вправо или влево.

Применим машину к слову | |.

1)

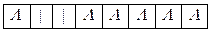
2)

3)

4)

5)

6)

7)

8)

9)

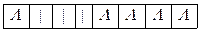
10)

11)

12)

13)

14)

15)

Состояние q₀ – заключительное, поэтому машина заканчивает работу.

Введение новой буквы α и замена исходных | на α позволяет различать исходные | и новые (приписанные). Состояние q₁ обеспечивает замену | на α, состояние q₂ обеспечивает поиск α, предназначенных для замены на |, и останов машины, если α не обнаружено, q₃ обеспечивает дописывание | в случае, когда произошла замена α на |.

Существуют следующие стандартные машины Тьюринга.

1. Тождественная машина Е – применима к любому слову u над алфавитом А и E(u) = u.

3. Пусть А – алфавит и (α. β) 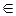А (α ≠ β). Машиной, заменяющейα на β, называется машина З_α←β, применимая к любому слову u, так что

З_α←β(u) =

Теорема. Тождественная. копирующая и заменяющая машины существуют.

Не нашли то, что искали? Google вам в помощь!

Источник

Применима ли машина Тьюринга?

Выяснить, применима ли машина Тьюринга, заданная программой P к слову S, и если применима, то указать результат применения машины Тьюринга к данному слову.

Выяснить, применима ли машина Тьюринга, заданная программой Р к слову S и, если применима, то указать результат
Выяснить, применима ли машина Тьюринга, заданная программой Р к слову S и, если применима, то.

Применима ли машина Тьюринга к последовательности символов?
Задание применима ли машина Тьюринга для алфавита А= <0,1>к последовательности символам на ленте.

А я не прошу за меня её делать.
Я её сам делаю. Потом, выставляю на обозрение ответ. А правильный или неправильный, решают форумчане. )))
И только потом, я начинаю задавать вопросы. когда сам начинаю не понимать(((
А пока это только задача, с которой мне приходиться бороться. )))
Не обижайтесь. Я просто не успеваю охватить, тот поток информации, который на меня льётся.
Поэтому, сначала задача, потом решение. И решение, не факт, что появится сегодня или завтра (т.к. я над ним работаю, листая разнообразную литературу).

А вот и я, добрался до форума.
Полистав некоторую литературу понял, что там сложного не так много.
Итак:
во-первых, слово я не то вставил.

во-вторых, моё решение:

Добавлено через 36 минут
ОШИБОЧКА в первой строчке.
там должно быть 111101. Но ответ от этого не изменится.

Согласен с решением.

Все-таки, мне кажется, до тех пор, пока вы серьезно не попытаетесь решить задачу и у вас не возникнут конкретные вопросы, на форум задачу постить не стоит.

Добавлено через 2 минуты

Выяснить, применима ли машина Тьюринга T к слову P?
Почему мой ответ неверен? Выяснить, применима ли машина Тьюринга T к слову P. Если применима, то.

Правила, когда применима машина Тьюринга к слову
Возник вопрос, применима ли машина Тьюринга к слову, если выполнение не останавливается? она в двух.

Выяснить, применима ли машина Тьюринга, заданная программой Р, к слову S
Что-то очень подозрительное с Машиной Тьюринга Здравствуйте! Нужно решить задачу, но не могу.

Источник

Свойства машины Тьюринга как алгоритма

На примере машины Тьюринга хорошо прослеживаются свойства алгоритмов. Попросите учащихся показать, что машина Тьюринга обладает всеми свойствами алгоритма.

Дискретность.Машина Тьюринга может перейти к (к + 1)-му шагу только после выполнения к-го шага, т.к. именно к-й шаг определяет, каким будет (к + 1)-й шаг.

Понятность.На каждом шаге в ячейку пишется символ из алфавита, автомат делает одно движение (Л, П, Н), и машина Тьюринга переходит в одно из описанных состояний.

Детерминированность.В каждой клетке таблицы машины Тьюринга записан лишь один вариант действия. На каждом шаге результат определен однозначно, следовательно, последовательность шагов решения задачи определена однозначно, т.е. если машине Тьюринга на вход подают одно и то же входное слово, то выходное слово каждый раз будет одним и тем же.

Результативность.Содержательно результаты каждого шага и всей последовательности шагов определены однозначно, следовательно, правильно написанная машина Тьюринга за конечное число шагов перейдет в состояние q0, т.е. за конечное число шагов будет получен ответ на вопрос задачи.

Массовость.Каждая машина Тьюринга определена над всеми допустимыми словами из алфавита, в этом и состоит свойство массовости. Каждая машина Тьюринга предназначена для решения одного класса задач, т.е. для каждой задачи пишется своя (новая) машина Тьюринга.

3Практическая часть

Задача 3.1 Выяснить, применима ли машина Тьюринга T к слову P. Если применима, то выписать результат T(P) применения машины Тьюринга T к слову P.

Предполагается, что начальный момент Машина Тьюринга обозревает самую левую единицу слова.

Решение. По определению команд машины Тьюринга получаем последовательность конфигураций

Так как команда, начинающаяся символами q2 1 в программе отсутствует, то последняя конфигурация является заключительной. Следовательно, машина Тьюринга применима к слову P и T(P)=1101

Задача 3.2 Требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.

Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:

	…
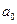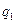	1 H	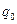1 H	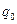2 H	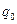3 H	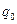4 H	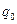5 H	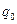…	8 H	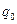9 H	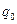0 Л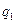

В этой машине Тьюринга q₁ — состояние изменения цифры, q₀ — состояние останова. Если в состоянии q_l автомат видит цифру 0..8, то он заменяет ее на 1..9 соответственно и переходит в состояние q₀, т.е. машина останавливается. Если же он видит цифру 9, то заменяет ее на 0, сдвигается влево, оставаясь в состоянии q_l. Так продолжается до тех пор, пока автомат не встретит цифру меньше 9. Если же все цифры были равны 9, то он заменит их нулями, запишет 0 на месте старшей цифры, сдвинется влево и в пустой клетке запишет 1. Затем перейдет в состояние q₀, т.е. остановится.

Источник