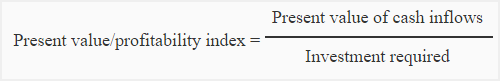How to calculate npv
How to calculate npv
Net Present Value (NPV)
Investopedia / Julie Bang
What Is Net Present Value (NPV)?
Net present value (NPV) is the difference between the present value of cash inflows and the present value of cash outflows over a period of time. NPV is used in capital budgeting and investment planning to analyze the profitability of a projected investment or project. NPV is the result of calculations used to find the current value of a future stream of payments.
Key Takeaways
Understanding Net Present Value
Net Present Value (NPV) Formula
If there’s one cash flow from a project that will be paid one year from now, then the calculation for the NPV is as follows:
If analyzing a longer-term project with multiple cash flows, then the formula for the NPV of a project is as follows:
If you are unfamiliar with summation notation, here is an easier way to remember the concept of NPV:
What Net Present Value Can Tell You
NPV accounts for the time value of money and can be used to compare the rates of return of different projects, or to compare a projected rate of return with the hurdle rate required to approve an investment. The time value of money is represented in the NPV formula by the discount rate, which might be a hurdle rate for a project based on a company’s cost of capital. No matter how the discount rate is determined, a negative NPV shows the expected rate of return will fall short of it, meaning the project will not create value.
In the context of evaluating corporate securities, the net present value calculation is often called discounted cash flow (DCF) analysis. It’s the method Warren Buffett uses to compare the net present value of a company’s discounted future cash flows with its current price.
The discount rate is central to the formula. It accounts for the fact that, so long as interest rates are positive, a dollar today is worth more than a dollar in the future. Inflation erodes the value of money over time. Meanwhile, today’s dollar can be invested in a safe asset like government bonds; investments riskier than Treasuries must offer a higher rate of return. However it’s determined, the discount rate is simply the baseline rate of return that a project must exceed to be worthwhile.
Positive vs. Negative NPV
A positive NPV indicates that the projected earnings generated by a project or investment—discounted for their present value—exceed the anticipated costs, also in today’s dollars. It is assumed that an investment with a positive NPV will be profitable.
An investment with a negative NPV will result in a net loss. This concept is the basis for the Net Present Value Rule, which says only investments with a positive NPV should be considered.
NPV can be calculated using tables, spreadsheets (for example, Excel), or financial calculators.
How To Calculate NPV Using Excel
In Excel, there is a NPV function that can be used to easily calculate the net present value of a series of cash flows. The NPV function in Excel is simply NPV, and the full formula requirement is:
=NPV(discount rate, future cash flow) + initial investment
In the example above, the formula entered into the gray NPV cell is:
=NPV(green cell, yellow cells) + blue cell
= NPV(C3, C6:C10) + C5
Example of Calculating Net Present Value
There are two key steps for calculating the NPV of the investment in equipment:
Step 1: NPV of the initial investment
Step 2: NPV of future cash flows
Assume the monthly cash flows are earned at the end of the month, with the first payment arriving exactly one month after the equipment has been purchased. This is a future payment, so it needs to be adjusted for the time value of money. An investor can perform this calculation easily with a spreadsheet or calculator. To illustrate the concept, the first five payments are displayed in the table below.
Image by Sabrina Jiang © Investopedia 2020
That formula can be simplified to the following calculation:
In this case, the NPV is positive; the equipment should be purchased. If the present value of these cash flows had been negative because the discount rate was larger or the net cash flows were smaller, the investment would not have made sense.
Limitations of Net Present Value
A notable limitation of NPV analysis is that it makes assumptions about future events that may not prove correct. The discount rate value used is a judgment call, while the cost of an investment and its projected returns are necessarily estimates. The net present value calculation is only as reliable as its underlying assumptions.
NPV Formula
Considers the time value of money
Incorporates discounted cash flow using a company’s cost of capital
Returns a single dollar value that is relatively easy to interpret
May be easy to calculate when leveraging spreadsheets or financial calculators
Relies heavily on inputs, estimates, and long-term projections
Doesn’t consider project size or ROI
May be hard to calculate manually, especially for projects with many years of cash flow
Is driven by quantitative inputs and does not consider non-financial metrics
Net Present Value vs. Payback Period
The payback period, or payback method, is a simpler alternative to NPV. The payback method calculates how long it will take to recoup an investment. One drawback of this method is that it fails to account for the time value of money. For this reason, payback periods calculated for longer-term investments have a greater potential for inaccuracy.
Moreover, the payback period calculation does not concern itself with what happens once the investment costs are nominally recouped. An investment’s rate of return can change significantly over time. Comparisons using payback periods assume otherwise.
NPV vs. Internal Rate of Return (IRR)
The internal rate of return (IRR) is calculated by solving the NPV formula for the discount rate required to make NPV equal zero. This method can be used to compare projects of different time spans on the basis of their projected return rates.
For example, IRR could be used to compare the anticipated profitability of a three-year project with that of a 10-year one. Although the IRR is useful for comparing rates of return, it may obscure the fact that the rate of return on the three-year project is only available for three years, and may not be matched once capital is reinvested.
What Does the Net Present Value Mean?
Net present value (NPV) is a financial metric that seeks to capture the total value of an investment opportunity. The idea behind NPV is to project all of the future cash inflows and outflows associated with an investment, discount all those future cash flows to the present day, and then add them together. The resulting number after adding all the positive and negative cash flows together is the investment’s NPV. A positive NPV means that, after accounting for the time value of money, you will make money if you proceed with the investment.
What Is the Difference Between NPV and IRR?
NPV and IRR are closely related concepts, in that the IRR of an investment is the discount rate that would cause that investment to have an NPV of zero. Another way of thinking about this is that NPV and IRR are trying to answer two separate but related questions. For NPV, the question is, “What is the total amount of money I will make if I proceed with this investment, after taking into account the time value of money?” For IRR, the question is, “If I proceed with this investment, what would be the equivalent annual rate of return that I would receive?”
What Is a Good NPV?
Why Are Future Cash Flows Discounted?
NPV uses discounted cash flows to account for the time value of money. So long as interest rates are positive, a dollar today is worth more than a dollar tomorrow because a dollar today can earn an extra day’s worth of interest. Even if future returns can be projected with certainty they must be discounted for the fact time must pass before they’re realized, time during which a comparable sum could earn interest.
Net Present Value (NPV) Calculator
How to Calculate Net Present Value
Net present value (NPV) is the present value of all future cash flows of a project. Because the time-value of money dictates that money is worth more now than it is in the future, the value of a project is not simply the sum of all future cash flows. Those future cash flows must be discounted because the money earned in the future is worth less today. In order to calculate NPV, we must discount each future cash flow in order to get the present value of each cash flow, and then we sum those present values associated with each time period.
You can think of NPV in different ways, but I think the easiest way is to think of it is as the sum of the present value all cash inflows, i.e. cash you earn from the project, less the present value of all cash outflows, i.e. cash you spend on the project. This way of thinking about NPV breaks it down into two parts, but the formula takes care of both of these parts simultaneously. The way we calculate the present value is through our discount rate, r, which is the rate of return we could expect from alternative projects. Say you have a dollar. If you don’t invest that dollar, you will still have that same dollar bill in your pocket next year; however, if you invest it, you could have more than that dollar one year from now. The alternative project is investing the dollar, and the rate of return for that alternative project is the rate that your dollar would grow over one year.
Just by thinking of things intuitively by the time value of money, if you have a time series of identical cash flows, the cash flow in the first time period will be the most valuable, the cash flow in the second time period will be the second most valuable, and so forth. This means that the present value of the cash flows decreases. Now, this is not always the case, since cash flows typically are variable; however, we must still account for time. The way we do this is through the discount rate, r, and each cash flow is discounted by the number of time periods that cash flow is away from the present date. This means that our cash flow for the first time period of the project would be discounted once, the cash flow in the second time period would be discounted twice, and so forth. To discount a cash flow, simply divide the cash flow by one plus the discount rate, raised to the number of periods you are discounting. This methodology follows from compound interest. Let’s take a look at an example.
Example
It is usually easiest both to see and set up the calculation by looking at a table of cash flows. You might consider setting up a table for this project that looks something like that of the one below:
| Rate | 0.06 | |||
|---|---|---|---|---|
| Year | 0 | 1 | 2 | 3 |
| CF | $(500,000) | $210,000 | $237,000 | $265,000 |
We discount our first cash flow, a cash outflow to be precise, by zero years. This just means that we really aren’t discounting the first cash flow because you would be paying for the project at the present time, so the present value of the first cash flow is just that, the first cash flow at face value. The other cash flows will need to be discounted by the number of years associated with each cash flow. We discount our cash flow earned in Year 1 once, our cash flow earned in Year 2 twice, and our cash flow earned in Year 3 thrice. Once we calculate the present value of each cash flow, we can simply sum them, since each cash flow is time-adjusted to the present day. Once we sum our cash flows, we get the NPV of the project. In this case, our net present value is positive, meaning that the project is a worthwhile endeavor. Be careful, however, because the projected cash flows are estimates typically, as is the discount rate. Our final calculation is only as good as its inputs.
What Is the Formula for Calculating Net Present Value (NPV)?
Net present value (NPV) is a method used to determine the current value of all future cash flows generated by a project, including the initial capital investment. It is widely used in capital budgeting to establish which projects are likely to turn the greatest profit.
The formula for NPV varies depending on the number and consistency of future cash flows.
Key Takeaways
Click Play to Learn the Net Present Value Formula
What Is Net Present Value?
Net present value is a capital budgeting analysis technique used to determine whether a long-term project will be profitable. The premise of the NPV formula is to compare an initial investment to the future cash flows of a project.
In general, the NPV formula strives to pull all future cash flow values to what each cash flow is worth today. Then, the NPV formula compares the value of those cash inflows against the initial investment or cash outflow. If the NPV of a project is positive (discounted future cash flow is greater than the initial investment), a project is expected to be profitable. If the NPV is negative, the initial investment is greater than the future cash flows.
NPV Formula
If there’s one cash flow from a project that will be paid one year from now, then the calculation for the NPV is as follows:
If analyzing a longer-term project with multiple cash flows, then the formula for the NPV of a project is as follows:
If you are unfamiliar with summation notation, here is an easier way to remember the concept of NPV:
How To Calculate NPV Using Excel
In Excel, there is a NPV function that can be used to easily calculate net present value of a series of cash flow. The NPV function in Excel is simply NPV, and the full formula requirement is:
=NPV(discount rate, future cash flow) + initial investment
In the example above, the formula entered into the grey NPV cell is:
=NPV(green cell, yellow cells) + blue cell
= NPV(C3, C6:C10) + C5
A series of future cash flows can alternate between positive and negative returns. After an initial cash outflow, a company may expect to need to repair equipment, pay property taxes on land, or incur selling costs for a given number of capital projects.
Dissecting the NPV Formula
The NPV formula has several important parts to it. Although the formula may be different for different types of cash flow streams, these four components are usually vital in calculating NPV.
Initial Investment
When analyzing NPV, it’s common for a series of cash flow to start with an initial investment. This cash outflow is represented s a negative cash outflow that will be used to compare the (hopefully) positive cash flow in the future. It is also common to assume that the investment will happen in period 0 (the initial period prior to the investment being implemented).
Future Cash Flow
The premise of NPV is centered around what the future cash flow will be. It’s assumed that after an initial investment, the investment will yield positive cash flow in the future. This cash flow may occur one time in the future, multiple times in the future for different amounts, or multiple times in the future for a consistent cashflow.
Interest Rate
The interest rate in the NPV formula is also referred to as the discount rate. This rate is used to determine what a dollar amount in the future is worth today. A company internally sets this rate, and companies often use the cost of capital to set this rate. For example, if it costs 4% to issue additional debt or shareholders expect a 6% dividend, a company may choose to use either of those rates.
With our machinery example, a company may expect its cost of capital to be 5%. Therefore, every cash flow will be discounted using a rate of 5%, though different discounts will be applied to each varying year of cash flow.
Time Period
Though already touched on early, it is implied that the time period must be considered for an investment. A company may make a one-time upfront investment; however, it may expect cash flow benefits for decades in the future. If the company expects a one-time cash flow in the future, it must identify the time period when they expect the return.
NPV’s counterpart is called the internal rate of return (IRR). While NPV returns a dollar value of net discounted cash flow from a project, IRR returns an expected rate of return that can used to compared across projects.
Examples Using NPV
The required rate of return is used as the discount rate for future cash flows to account for the time value of money. A dollar today is worth more than a dollar tomorrow because a dollar can be put to use earning a return. Therefore, when calculating the present value of future income, cash flows that will be earned in the future must be reduced to account for the delay.
NPV is used in capital budgeting to compare projects based on their expected rates of return, required investment, and anticipated revenue over time. Typically, projects with the highest NPV are pursued.
For example, consider two potential projects for company ABC.
Both projects require the same initial investment, but Project X generates more total income than Project Y. However, Project Y has a higher NPV because income is generated faster (meaning that the discount rate has a smaller effect).
Advantages of NPV Formula
The NPV formula leverages the time value of money; compared to other capital budgeting analysis tools, the NPV formula discounts cash flow and analyzes profitability based on the timing of when cash flow occurs. The NPV formula also factors in the company’s specific cost of capital via the discount rate.
By discounting cash flow, the NPV formula naturally builds in long-term exposure to risk. The furthest estimates in the future are discounted most heavily, appropriately factoring in that these cash flows often have the most uncertainty.
The NPV formula often produces a calculation that is easily interpretable. If the finding is positive, the project is profitable. If the finding is negative, the project is not profitable. As opposed to the IRR formula which produces a percentage that has to be compared against a benchmark, NPV yields value on its own.
Limitations of NPV Formula
Like other financial formulas used for strategic planning, the NPV formula is only as valuable as the inputs. The NPV formula relies heavily on the quality of information provided, even though estimates may range decades into the future.
NPV Formula
Considers the time value of money
Incorporates discounted cash flow using a company’s cost of capital
Returns a single dollar value that is relatively easy to interpret
May be easy to calculate when leveraging spreadsheets or financial calculators
Relies heavily in inputs, estimates, and long-term projections
Doesn’t distinguish between project sizes or ROI
May be found as complex and difficult to manually calculate, especially for projects with many years of cash flow
Is driven by quantitative inputs and does not consider non-financial metrics
How Is NPV Calculated?
NPV is calculated by taking the present value of all cash flows over the life of a project. Then, the present value of cash flows is subtracted from the investment’s initial investment. If the difference is positive (greater than 0), the project will be profitable.
What Is Net Present Value (NPV) Used For?
Net present value (NPV) is used in capital budgeting to determine whether a project will be profitable, or to evaluate different projects and determine which one will be the most profitable.
What Is the Main Advantage of NPV Over an Alternative Method Like the Payback Period?
The main advantage of the NPV method is that it takes into consideration the time value of money, by discounting future cash flows at an appropriate discount rate that is based on the company’s cost of capital and the project’s risk. The payback period estimates how long it will take for a project to generate sufficient cash flows to pay back its initial startup costs, but it does not consider the time value of money and overall project profitability like NPV does.
What Are the Main Drawbacks of NPV?
NPV needs accurate assumptions for a number of variables like initial costs and future cash flows—and, most importantly, the discount rate or cost of capital. As small changes in the discount rate can lead to significant swings in the discounted value of future cash flows, inaccurate discount rates may lead to incorrect NPV and hence an erroneous decision on the project’s profitability and viability.
What Does a Negative NPV Number Mean?
A negative NPV number means that a project will be unprofitable as the initial startup costs exceed the discounted value of net future cash flows.
The Bottom Line
Net present value (NPV) discounts all the future cash flows from a project and subtracts its required investment. The analysis is used in capital budgeting to determine if a project should be undertaken compared to alternative uses of capital or other projects.
Net present value method
Net present value method (also known as discounted cash flow method) is a popular capital budgeting technique that takes into account the time value of money. It uses net present value of the investment project as the base to accept or reject a proposed investment in projects like purchase of new equipment, purchase of inventory, expansion or addition of existing plant assets and the installation of new plants etc.
First, I would explain what is net present value and then how it is used to analyze investment projects.
Net present value (NPV):
Net present value is the difference between the present value of cash inflows and the present value of cash outflows that occur as a result of undertaking an investment project. It may be positive, zero or negative. These three possibilities of net present value are briefly explained below:
Positive NPV:
If present value of cash inflows is greater than the present value of the cash outflows, the net present value is said to be positive and the investment proposal is considered to be acceptable.
Zero NPV:
If present value of cash inflow is equal to present value of cash outflow, the net present value is said to be zero and the investment proposal is considered to be acceptable.
Negative NPV:
If present value of cash inflow is less than present value of cash outflow, the net present value is said to be negative and the investment proposal is rejected.
The summary of the concept explained so far is given below:
The following example illustrates the use of net present value method in analyzing an investment proposal.
Example 1 – cash inflow project:
Required:
Solution:
(1) Computation of net present value:
(2) Purchase decision:
Yes, the equipment should be purchased because the net present value is positive ($1,317). Having a positive net present value means the project promises a rate of return that is higher than the minimum rate of return required by management (20% in the above example).
In the above example, the minimum required rate of return is 20%. It means if the equipment is not purchased and the money is invested elsewhere, the company would be able to earn 20% return on its investment. The minimum required rate of return (20% in our example) is used to discount the cash inflow to its present value and is, therefore, also known as discount rate.
Investments in assets are usually made with the intention to generate revenue or reduce costs in future. The reduction in cost is considered equivalent to increase in revenues and should, therefore, be treated as cash inflow in capital budgeting computations.
The net present value method is used not only to evaluate investment projects that generate cash inflow but also to evaluate projects that can reduce costs. The following example illustrates how this capital budgeting method can be applied to analyze a cost reduction project:
Example 2 – cost reduction project:
Should Smart Manufacturing Company purchase the machine?
Solution:
According to net present value method, Smart Manufacturing Company should purchase the machine because the present value of the cost savings is greater than the present value of the initial cost to purchase and install the machine. The computations are given below:
Net present value method – uneven cash flow:
Notice that the projects in the above examples generate equal cash inflow in all the periods (the cost saving in example 2 has been treated as cash inflow). Such a flow of cash is known as even cash flow. But sometimes projects do not generate equal cash inflows in all the periods. When projects generate different cash inflows in different periods, the flow of cash is known as uneven cash flow. To analyze such projects the present value of the inflow of cash is computed for each period separately. It has been illustrated in the following example:
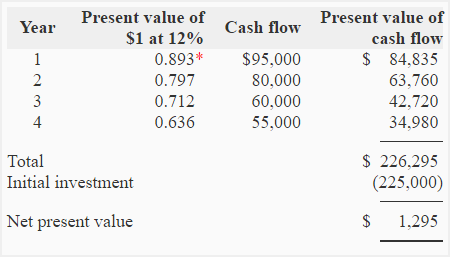
Example 3:
Required: Compute net present value of the project if the minimum desired rate of return is 12%.
Solution:
The cash inflow generated by the project is uneven. Therefore, the present value would be computed for each year separately:
The project seems attractive because its net present value is positive.
Choosing among several alternative investment proposals:
Sometime a company may have limited funds but several alternative proposals. In such circumstances, if each alternative requires the same amount of investment, the one with the highest net present value is preferred. But if each proposal requires a different amount of investment, then proposals are ranked using an index called present value index (or profitability index). The proposal with the highest present value index is considered the best. Present value index is computed using the following formula:
Formula of present value or profitability index:
Example 4:
Choose the most desirable investment proposal from the following alternatives using profitability index method:
Solution:
Because each investment proposal requires a different amount of investment, the most desirable investment can be found using present value index. Present value index of all three proposals is computed below:
Proposal X: 212,000/200,000 = 1.06
Proposal Y: 171,800/160,000 = 1.07
Proposal Z: 185,200/180,000 = 1.03
Proposal X has the highest net present value but is not the most desirable investment. The present value indexes show proposal Y as the most desirable investment because it promises to generate 1.07 present value for each dollar invested, which is the highest among three alternatives.
Assumptions:
The net present value method is based on two assumptions. These are:
Advantages and Disadvantages:
The basic advantage of net present value method is that it considers the time value of money. The disadvantage is that it is more complex than other methods that do not consider present value of cash flows. Furthermore, it assumes immediate reinvestment of the cash generated by investment projects. This assumption may not always be reasonable due to changing economic conditions.
:max_bytes(150000):strip_icc()/jason_mugshot__jason_fernando-5bfc261946e0fb00260a1cea.jpg)
:max_bytes(150000):strip_icc()/mansaPicture_08T-Copy-JuliusMansa-127908fd255745b5886a16fced0cdb7b.jpg)
:max_bytes(150000):strip_icc()/E7F37E3D-4C78-4BDA-9393-6F3C581602EB-2c2c94499d514e079e915307db536454.jpeg)
:max_bytes(150000):strip_icc()/dotdash_Final_Net_Present_Value_NPV_Jul_2020-01-eea50904f90744e4b1172a9ef38df13f.jpg)
:max_bytes(150000):strip_icc()/johnheadshot2017__john_jagerson-5bfc2618c9e77c00262f60f3.jpg)
:max_bytes(150000):strip_icc()/JamesHeadshot-PeggyJames-9f712f1197374a9b824289fe0d5ec842.jpg)
:max_bytes(150000):strip_icc()/TimothyLi-picture1-4fb5c746f503451bacfee414a08f5c1f.jpg)