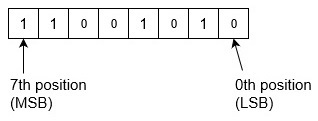
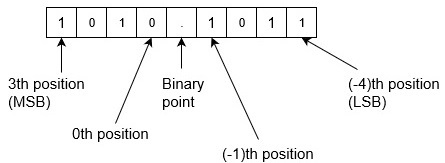
How to convert binary decimal to decimal
How to convert binary decimal to decimal
How to Convert Binary to Decimal?
Binary is the simplest kind of number system that uses only two digits of 0 and 1 (i.e. value of base 2). Since digital electronics have only these two states (either 0 or 1), so binary number is most preferred in modern computer engineer, networking and communication specialists, and other professionals.
Whereas Decimal number is most familiar number system to the general public. It is base 10 which has only 10 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Conversion from Binary to Decimal number system
There are mainly two methods to convert a binary number into decimal number − using positional notation, and using doubling. These methods are explained are as following below.
Using Positional Notation
This is simple algorithm where you have to multiply positional value of binary with their digit and get the sum of these steps.
Example-1 − Convert binary number 11001010 into decimal number. Since there is no binary point here and no fractional part. So,
Binary to decimal is,
Example-2 − Convert binary number 1010.1011 into decimal number. Since there is a binary point here with fractional part. So,
Binary to decimal is,
Using Doubling
This is simple method to convert a binary number into decimal number, you need to start from leftmost digit (or MSB) from the input. Take the most significant bit (MSB), right down, then multiply by 2 with it and add second leftmost bit, store it as current result, then again multiple by 2 with current result and add third leftmost bit, update this value as current result and follow this till addition of least significant bit (LSB or rightmost bit). Since you are doubling (multiplying by 2) each time, so this method is known as Doubling.
These are simple algorithm is explained below in steps −
Write down the binary number.
Starting from the left, double your previous total and add the current digit.
Double your current total and add the next leftmost digit.
Repeat the previous step.
For example, Convert binary number 11101110 into decimal number. According to above algorithm, Binary to decimal is,
These are above two simple methods to convert a binary number into decimal number.
How to Convert from Binary to Decimal?
Binary numbers are numbers that are understandable by computer machines. It is in a combination of 0’s & 1’s. As computers and few electronic devices understood only binary language they take input only in binary format and returns result in binary format.
In this article, we are going to learn how to convert a binary number to a decimal.
Binary to Decimal Formula
To convert a binary number to decimal we need to perform a multiplication operation on each digit of a binary number from right to left with powers of 2 starting from 0 and add each result to get the decimal number of it.
This can be better explained using the below examples:
Example 1: Let’s consider a binary number 1111. We need to convert this binary number to a decimal number.
Solution:
As mentioned in the above paragraph while converting from binary to decimal we need to consider each digit in binary number from right to left.
By this way, we can do binary to decimal conversion.
Note: We represent any binary number with this format (xxxx)2 and decimal in (xxxx)10 format.
Example 2: Convert (101010)2->(?)10
Solution:
We keep on increasing the power of 2 as long as number of digits in binary number increases.
Example 3: Convert (11100)2->(?)10
Solution:
Resultant Decimal number = 0+0+4+8+16 = 28
There is also another method called Doubling that can be used to convert binary numbers to decimals.
Doubling Method
To explain this method we will consider an example and try to solve that stepwise.
Example 1: Convert Binary number (10001)2 to decimal.
Solution:
Similar to the above approach, In this approach also consider each digit but from left to right and performs step-wise computations on it.
| 1 | 0 | 0 | 0 | 1 |
Step-1 First we need to multiply 0 with 2 and add the 1st digit in binary number.
0 x 2 + 1 = 0 + 1 = 1
Step-2 Now use the result of above step and multiply with 2 and add the second digit of binary number.
0
1 x 2 + 0 = 2 + 0 = 2
The same step 2 is repeated until there will be no digit left. The final result will be the resultant decimal number.
0
2 x 2 + 0 = 4 + 0 = 4
0
4 x 2 + 0 = 8 + 0 = 8
Convert Binary to Decimal!
This Binary to Decimal Converter lets you convert Binary numbers to decimal quickly and easily.
Rate this converter
[Total: 74 Average: 4.4 ]
How to use the Binary to Decimal Converter
Time needed: 1 minute.
Enter a Binary Number in the first field.
Press the Convert button below the binary number field.
The Decimal Number output will appear in the second field.
Optionally, you can Copy the output to clipboard, or Save it as a file on your device.
Converter features
| 🔟 Binary Input length: | Up to 25 digits |
| ⚡ Conversion Speed: | Instant! |
| ➡️ Decimal Output: | Display, Copy, Save |
| 🎯 Conversion Accuracy: | 100% |
Read (or watch) our tutorial on How to Convert Binary to Decimal to learn more about the process of converting binary numbers to decimal.
How to Convert Binary to Decimal
So, you need to know how to convert binary to decimal? All those ones and zeros can be intimidating. You can find a binary to decimal converter here, or you can learn to convert yourself – no computer required.
If you thought complicated formulas were necessary for binary to decimal conversion, you can breathe a sigh of relief. To convert from binary number system to decimal number system, you really only need to know three things. First, remember that the ones and zeros that make up binary can be thought of as the answer to a yes or no question. One for “yes”, and zero for “no”. Next, if you have an understanding of the powers of 2, this will be a breeze. The last step is basic addition.
The (Super) Powers of 2
Let’s look at a three-digit binary number, 101.
To convert 101 in binary to decimal, we’ll must use the first three powers of 2. The most straightforward way to visualize this is to write your binary number, and above it, fill in powers of 2. Just remember to start from 2 0 on the right, and work your way left until you’ve run out of binary digits.
We have 1, 0, and 1, and a power of 2 for each binary digit. We start from the rightmost digit, which is the Least Significant Bit (LSB): look at 2 0 ; what’s underneath it? A one. This indicates we will use 2 0 in the decimal output.
Now, let’s work on the next leftmost digit. What’s under 2¹? A zero. This means we will not use 2¹. And under 2²? Another one. To find out what 101 is in decimal, we’ll need 2 0 and 2².
The rest is simple – 2 0 and 2² are 1 and 4, respectively. Now just add 1 + 4. The binary number 101 is the decimal 5.
Just remember to always proceed from right to left, or from the Least Significant Bit (LSB, the rightmost digit) to the Most Significant Bit (MSB, the leftmost digit).
It’s incredibly easy once you can think of 1 as a “yes”, and 0 as a “no”. Bigger numbers work in the same way. Let’s throw some extra zeros into the mix and use 100001. It’s long, but the method is identical. We just need 6 powers of 2 this time; one for each digit in the binary number.
Just to prove how simple converting binary to decimal is, let’s look at an even longer binary figure: 11001100. We’ll need to go all the way to 2 7 for this conversion.
All we need to do is add the powers of 2 we used. Remember, we only “use” them when they correspond to a one. In this case, we need to add 128, 64, 8, and 4 to find the decimal. Everything else is indicated by a zero, so we don’t need to include them! 11001100 in binary is the decimal 204.
If you want to try it out for yourself, you can use the binary to decimal calculator on this page to check your work. Practice a few times, and you’ll be speaking the language of computers with ease.
Table of the First hundred Binary numbers in Decimal
For your convenience, the following table shows the binary numbers from 0 to 1100100 along with their Decimal representation.
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
| 10101 | 21 |
| 10110 | 22 |
| 10111 | 23 |
| 11000 | 24 |
| 11001 | 25 |
| 11010 | 26 |
| 11011 | 27 |
| 11100 | 28 |
| 11101 | 29 |
| 11110 | 30 |
| 11111 | 31 |
| 100000 | 32 |
| 100001 | 33 |
| 100010 | 34 |
| 100011 | 35 |
| 100100 | 36 |
| 100101 | 37 |
| 100110 | 38 |
| 100111 | 39 |
| 101000 | 40 |
| 101001 | 41 |
| 101010 | 42 |
| 101011 | 43 |
| 101100 | 44 |
| 101101 | 45 |
| 101110 | 46 |
| 101111 | 47 |
| 110000 | 48 |
| 110001 | 49 |
| 110010 | 50 |
| 110011 | 51 |
| 110100 | 52 |
| 110101 | 53 |
| 110110 | 54 |
| 110111 | 55 |
| 111000 | 56 |
| 111001 | 57 |
| 111010 | 58 |
| 111011 | 59 |
| 111100 | 60 |
| 111101 | 61 |
| 111110 | 62 |
| 111111 | 63 |
| 1000000 | 64 |
| 1000001 | 65 |
| 1000010 | 66 |
| 1000011 | 67 |
| 1000100 | 68 |
| 1000101 | 69 |
| 1000110 | 70 |
| 1000111 | 71 |
| 1001000 | 72 |
| 1001001 | 73 |
| 1001010 | 74 |
| 1001011 | 75 |
| 1001100 | 76 |
| 1001101 | 77 |
| 1001110 | 78 |
| 1001111 | 79 |
| 1010000 | 80 |
| 1010001 | 81 |
| 1010010 | 82 |
| 1010011 | 83 |
| 1010100 | 84 |
| 1010101 | 85 |
| 1010110 | 86 |
| 1010111 | 87 |
| 1011000 | 88 |
| 1011001 | 89 |
| 1011010 | 90 |
| 1011011 | 91 |
| 1011100 | 92 |
| 1011101 | 93 |
| 1011110 | 94 |
| 1011111 | 95 |
| 1100000 | 96 |
| 1100001 | 97 |
| 1100010 | 98 |
| 1100011 | 99 |
| 1100100 | 100 |
Questions and Answers about Binary to Decimal conversion
The Binary to Decimal Converter at ConvertBinary.com is really easy to use.
Just follow these steps: enter your binary number in the first field, then push the “Convert” button.
The decimal representation for your binary number will immediately appear in the field below.
To convert binary numbers to their decimal equivalent, you have two options: you can either use an online converter (like the one provided for free by ConvertBinary.com), or you can do it manually.
If you want to learn how to convert binary to decimal manually, you can read this guide, or watch the associated tutorial.
It uses a scripting function that parses the input (the binary number in our case) and returns an integer.
The function call specifies that the binary system should be used.
The process is automatic and so quick that it feels like it’s instant, even for very large numbers.
Of course! If you want to convert any decimal number to binary, you can use the Decimal to Binary Converter at ConvertBinary.com.
The binary number 1000 (one-zero-zero-zero) is 8 (eight) in Decimal.
Binary to Decimal
| 1. | What is Binary to Decimal Conversion? |
| 2. | Binary to Decimal Conversion Methods |
| 3. | Binary to Decimal Formula |
| 4. | Binary to Decimal Conversion Chart |
| 5. | Binary to Decimal Converter |
| 6. | FAQs on Binary to Decimal |
What is Binary to Decimal Conversion?
Binary to decimal conversion is done to represent a number given in Binary Number System to its equivalent in the Decimal Number System. A number system is very essential to represent numbers. Every number system has a base and the base of a number system is determined by the total number of digits used in the number system. For example, the binary number system has a base of 2 because it has only two digits to represent any number. Similarly, the decimal number system has a base of 10, as it has 10 digits to represent a number.
The conversion of numbers from binary to decimal is important as it helps to read numbers that are represented as a set of 0s and 1s. Let us learn about the different binary to decimal conversion methods and examples.
Binary to Decimal Conversion Methods
Binary to decimal conversion is done to help read large binary numbers easily in a form that humans can understand. There are two methods to convert a number from binary to decimal number system.
Let us understand these binary to decimal conversion methods in detail.
Binary to Decimal Conversion Using Positional Notation Method
The positional notation method is one in which the value of a digit in a number is determined by a weight based on its position. This is achieved by multiplying each digit by the base (2) raised to the respective power depending upon the position of that digit in the number. The sum of all these values obtained for each digit gives the equivalent value of the given binary number in the decimal system. Let us understand this with the help of examples.
Example: Convert the binary number 1011012 to a decimal number.
Binary to Decimal Conversion Using Doubling Method
As the name suggests, the process of doubling or multiplying by 2 is done to convert binary to decimal. Let us use the same example for converting the binary number 1011012 to decimal.
Example: Convert the binary number 1011012 to decimal using doubling method.
Solution: Observe the following steps given below to understand the binary to decimal conversion using the doubling method.
Observe the figure given below to relate to the steps and understand how the doubling method works.
Binary to Decimal Formula
In the previous section, we understood the methods and their stepwise process to convert a binary to a decimal. Let us learn the general formula for converting a binary number to a decimal number now. Considering dn to be the digits of a binary number consisting of ‘n’ digits, the formula to convert binary to decimal is given as,
Binary to Decimal Conversion Formula:
where, d0, d1, d2 are the individual digits of the binary number starting from the right-most position.
Let us see the application of the above binary to decimal formula and learn how to convert binary to decimal using the following example.
Example: Convert 11102, from binary to decimal using the binary to decimal formula.
= (0 × 2 0 ) + (1 × 2 1 ) + (1 × 2 2 ) + (1 × 2 3 )
= 0 + 2 + 4 + 8
= 14
Therefore, 11102 = 1410
Binary to Decimal Conversion Chart
The binary to decimal conversion of the first 20 decimal numbers is displayed in the chart given below.
| Binary | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
| 10000 | 16 |
| 10001 | 17 |
| 10010 | 18 |
| 10011 | 19 |
| 10100 | 20 |
Binary to Decimal Converter
☛ Related Articles
Examples on Binary to Decimal
Example 1: Find the decimal value of the binary number 110010112 using the positional notation method of binary to decimal conversion.
Solution:
By the positional notation of binary to decimal conversion, we multiply every digit in the binary number with its base raised to the power based on its position. This is done by starting from the rightmost digit and moving on to the left and summing up all the values.
In the binary to decimal conversion shown below, we start from the right and move towards the left.
110010112 = (1 × 2 0 )+ (1 × 2 1 )+ (0 × 2 2 )+ (1 × 2 3 ) + (0 × 2 4 ) + (0 × 2 5 ) + (1 × 2 6 ) + (1 × 2 7 )
= (1 × 1) + (1 × 2) + (0 × 4) + (1 × 8) + (0 × 16) + (0 × 32) + (1 × 64) + (1 × 128)
= 1 + 2 + 0 + 8 + 0 + 0 + 64 +128
= 203
Example 2: Using the doubling method of binary to decimal conversion, find the decimal value of 101011012
Solution:
For the binary to decimal conversion of a number using the doubling method, we use the following steps:
The steps that were discussed above for the binary to decimal conversion are shown below:
Example 3: Fill in the blanks with respect to binary to decimal conversion.
a.) 10112 binary to decimal is __.
b.) The binary number 101012 is equivalent to decimal number __.
Solution:
a.) 10112 binary to decimal is 11.
b.) The binary number 101012 is equivalent to decimal number 21.
Binary to Decimal Converter
In order to use this new binary to decimal converter tool, type any binary value like 1010 into the left field below, and then hit the Convert button. You can see the result in the right field below. It is possible to convert up to 63 binary characters to decimal.
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Decimal System
The decimal numeral system is the most commonly used and the standard system in daily life. It uses the number 10 as its base (radix). Therefore, it has 10 symbols: The numbers from 0 to 9; namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
As one of the oldest known numeral systems, the decimal numeral system has been used by many ancient civilizations. The difficulty of representing very large numbers in the decimal system was overcome by the Hindu–Arabic numeral system. The Hindu-Arabic numeral system gives positions to the digits in a number and this method works by using powers of the base 10; digits are raised to the n th power, in accordance with their position.
For instance, take the number 2345.67 in the decimal system:
How to Read a Binary Number
Example: The binary number (1010)2 can also be written as follows: (1 * 2 3 ) + (0 * 2 2 ) + (1 * 2 1 ) + (0 * 2 0 )
How to Convert Binary to Decimal
There are two methods to apply a binary to decimal conversion. The first one uses positional representation of the binary, which is described above. The second method is called double dabble and is used for converting longer binary strings faster. It doesn’t use the positions.
Method 1: Using Positions
Step 1: Write down the binary number.
Step 3: Add the results and you will get the decimal equivalent of the given binary number.
Now, let’s apply these steps to, for example, the binary number above, which is (1010)2
(Note that the digits 0 in the binary produced zero values in the decimal as well.)
Method 2: Double Dabble
Also called doubling, this method is actually an algorithm that can be applied to convert from any given base to decimal. Double dabble helps converting longer binary strings in your head and the only thing to remember is ‘double the total and add the next digit’.
Now, let’s apply the double dabble method to same the binary number, (1010)2
This is where you run out of digits in this example. Therefore, (1010)2 = (10)10
Binary to decimal conversion examples
Example 1: (1110010)2 = (114)10
Method 1:
(0 * 2 0 ) + (1 * 2 1 ) + (0 * 2 2 ) + (0 * 2 3 ) + (1 * 2 4 ) + (1 * 2 5 ) + (1 * 2 6 )
= (0 * 1) + (1 * 2) + (0 * 4) + (0 * 8) + (1 * 16) + (1 * 32) + (1 * 64)
= 0 + 2 + 0 + 0 + 16 + 32 + 64 = 114
Method 2:
0 (previous sum at starting point)
(0 + 1) * 2 = 2
2 + 1 = 3
3 * 2 =6
6 + 1 =7
7 * 2 = 14
14 + 0 =14
14 * 2 = 28
28 + 0 =28
28 * 2 = 56
56 + 1 = 57
57 * 2 = 114
Example 2: (11011)2 = (27)10
Method 1:
(0 * 2 0 ) + (1 * 2 1 ) + (0 * 2 2 ) + (1 * 2 3 ) + (1 * 2 4 )
= (1 * 1) + (1 * 2) + (0 * 4) + (1 * 8) + (1 * 16)
= 1 + 2 + 0 + 8 + 16 = 27
Method 2:
(0 * 2) + 1 = 1
(1 * 2) + 1 = 3
(3 * 2) + 0 = 6
(6 * 2) + 1 = 13
(13 * 2) + 1 = 27
Binary Decimal Conversion Chart Table
| Binary | Decimal |
|---|---|
| 00000001 | 1 |
| 00000010 | 2 |
| 00000011 | 3 |
| 00000100 | 4 |
| 00000101 | 5 |
| 00000110 | 6 |
| 00000111 | 7 |
| 00001000 | 8 |
| 00001001 | 9 |
| 00001010 | 10 |
| 00001011 | 11 |
| 00001100 | 12 |
| 00001101 | 13 |
| 00001110 | 14 |
| 00001111 | 15 |
| 00010000 | 16 |
| 00010001 | 17 |
| 00010010 | 18 |
| 00010011 | 19 |
| 00010100 | 20 |
| 00010101 | 21 |
| 00010110 | 22 |
| 00010111 | 23 |
| 00011000 | 24 |
| 00011001 | 25 |
| 00011010 | 26 |
| 00011011 | 27 |
| 00011100 | 28 |
| 00011101 | 29 |
| 00011110 | 30 |
| 00011111 | 31 |
| 00100000 | 32 |
| 00100001 | 33 |
| 00100010 | 34 |
| 00100011 | 35 |
| 00100100 | 36 |
| 00100101 | 37 |
| 00100110 | 38 |
| 00100111 | 39 |
| 00101000 | 40 |
| 00101001 | 41 |
| 00101010 | 42 |
| 00101011 | 43 |
| 00101100 | 44 |
| 00101101 | 45 |
| 00101110 | 46 |
| 00101111 | 47 |
| 00110000 | 48 |
| 00110001 | 49 |
| 00110010 | 50 |
| 00110011 | 51 |
| 00110100 | 52 |
| 00110101 | 53 |
| 00110110 | 54 |
| 00110111 | 55 |
| 00111000 | 56 |
| 00111001 | 57 |
| 00111010 | 58 |
| 00111011 | 59 |
| 00111100 | 60 |
| 00111101 | 61 |
| 00111110 | 62 |
| 00111111 | 63 |
| 01000000 | 64 |
| Binary | Decimal |
|---|---|
| 01000001 | 65 |
| 01000010 | 66 |
| 01000011 | 67 |
| 01000100 | 68 |
| 01000101 | 69 |
| 01000110 | 70 |
| 01000111 | 71 |
| 01001000 | 72 |
| 01001001 | 73 |
| 01001010 | 74 |
| 01001011 | 75 |
| 01001100 | 76 |
| 01001101 | 77 |
| 01001110 | 78 |
| 01001111 | 79 |
| 01010000 | 80 |
| 01010001 | 81 |
| 01010010 | 82 |
| 01010011 | 83 |
| 01010100 | 84 |
| 01010101 | 85 |
| 01010110 | 86 |
| 01010111 | 87 |
| 01011000 | 88 |
| 01011001 | 89 |
| 01011010 | 90 |
| 01011011 | 91 |
| 01011100 | 92 |
| 01011101 | 93 |
| 01011110 | 94 |
| 01011111 | 95 |
| 01100000 | 96 |
| 01100001 | 97 |
| 01100010 | 98 |
| 01100011 | 99 |
| 01100100 | 100 |
| 01100101 | 101 |
| 01100110 | 102 |
| 01100111 | 103 |
| 01101000 | 104 |
| 01101001 | 105 |
| 01101010 | 106 |
| 01101011 | 107 |
| 01101100 | 108 |
| 01101101 | 109 |
| 01101110 | 110 |
| 01101111 | 111 |
| 01110000 | 112 |
| 01110001 | 113 |
| 01110010 | 114 |
| 01110011 | 115 |
| 01110100 | 116 |
| 01110101 | 117 |
| 01110110 | 118 |
| 01110111 | 119 |
| 01111000 | 120 |
| 01111001 | 121 |
| 01111010 | 122 |
| 01111011 | 123 |
| 01111100 | 124 |
| 01111101 | 125 |
| 01111110 | 126 |
| 01111111 | 127 |
| 10000000 | 128 |
| Binary | Decimal |
|---|---|
| 10000001 | 129 |
| 10000010 | 130 |
| 10000011 | 131 |
| 10000100 | 132 |
| 10000101 | 133 |
| 10000110 | 134 |
| 10000111 | 135 |
| 10001000 | 136 |
| 10001001 | 137 |
| 10001010 | 138 |
| 10001011 | 139 |
| 10001100 | 140 |
| 10001101 | 141 |
| 10001110 | 142 |
| 10001111 | 143 |
| 10010000 | 144 |
| 10010001 | 145 |
| 10010010 | 146 |
| 10010011 | 147 |
| 10010100 | 148 |
| 10010101 | 149 |
| 10010110 | 150 |
| 10010111 | 151 |
| 10011000 | 152 |
| 10011001 | 153 |
| 10011010 | 154 |
| 10011011 | 155 |
| 10011100 | 156 |
| 10011101 | 157 |
| 10011110 | 158 |
| 10011111 | 159 |
| 10100000 | 160 |
| 10100001 | 161 |
| 10100010 | 162 |
| 10100011 | 163 |
| 10100100 | 164 |
| 10100101 | 165 |
| 10100110 | 166 |
| 10100111 | 167 |
| 10101000 | 168 |
| 10101001 | 169 |
| 10101010 | 170 |
| 10101011 | 171 |
| 10101100 | 172 |
| 10101101 | 173 |
| 10101110 | 174 |
| 10101111 | 175 |
| 10110000 | 176 |
| 10110001 | 177 |
| 10110010 | 178 |
| 10110011 | 179 |
| 10110100 | 180 |
| 10110101 | 181 |
| 10110110 | 182 |
| 10110111 | 183 |
| 10111000 | 184 |
| 10111001 | 185 |
| 10111010 | 186 |
| 10111011 | 187 |
| 10111100 | 188 |
| 10111101 | 189 |
| 10111110 | 190 |
| 10111111 | 191 |
| 11000000 | 192 |
| Binary | Decimal |
|---|---|
| 11000001 | 193 |
| 11000010 | 194 |
| 11000011 | 195 |
| 11000100 | 196 |
| 11000101 | 197 |
| 11000110 | 198 |
| 11000111 | 199 |
| 11001000 | 200 |
| 11001001 | 201 |
| 11001010 | 202 |
| 11001011 | 203 |
| 11001100 | 204 |
| 11001101 | 205 |
| 11001110 | 206 |
| 11001111 | 207 |
| 11010000 | 208 |
| 11010001 | 209 |
| 11010010 | 210 |
| 11010011 | 211 |
| 11010100 | 212 |
| 11010101 | 213 |
| 11010110 | 214 |
| 11010111 | 215 |
| 11011000 | 216 |
| 11011001 | 217 |
| 11011010 | 218 |
| 11011011 | 219 |
| 11011100 | 220 |
| 11011101 | 221 |
| 11011110 | 222 |
| 11011111 | 223 |
| 11100000 | 224 |
| 11100001 | 225 |
| 11100010 | 226 |
| 11100011 | 227 |
| 11100100 | 228 |
| 11100101 | 229 |
| 11100110 | 230 |
| 11100111 | 231 |
| 11101000 | 232 |
| 11101001 | 233 |
| 11101010 | 234 |
| 11101011 | 235 |
| 11101100 | 236 |
| 11101101 | 237 |
| 11101110 | 238 |
| 11101111 | 239 |
| 11110000 | 240 |
| 11110001 | 241 |
| 11110010 | 242 |
| 11110011 | 243 |
| 11110100 | 244 |
| 11110101 | 245 |
| 11110110 | 246 |
| 11110111 | 247 |
| 11111000 | 248 |
| 11111001 | 249 |
| 11111010 | 250 |
| 11111011 | 251 |
| 11111100 | 252 |
| 11111101 | 253 |
| 11111110 | 254 |
| 11111111 | 255 |
Recent Comments
really good. helps you save time
It was use full for me I got more thing to know from this i enjoyed a lot
It is so helpful for researchers on Bitcoin
@dilantaher 111.0101 = 7.3125
Your previous total 0. Your leftmost digit is 1. Double the total and add the leftmost digit
(0 * 2) + 1 = 1
Step 2: Double the previous total and add the next leftmost digit.
(1 * 2) + 0 = 2
Step 3: Double the previous total and add the next leftmost digit.
(2 * 2) + 1 = 5
Step 4: Double the previous total and add the next leftmost digit.
(5 * 2) + 0 = 10
17. “Schoolhouse Rock’ had a song called ‘Little Twelvetoes’ which had an alien character with 6 fingers on each hand who could count by 12 as easily as we count by 10. If he counted to 100 in his base 12 (duodecimal), what would that be in decimal?
plz help me
Answer?
Assign a binary code in some orderly manner to the 52 playing cards. Use the minimum number of bits. (4)
plz help me
plz send me solution of this question