How to round float in python
How to round float in python
Python round() function with EXAMPLES
Updated July 9, 2022
Round()
Round() is a built-in function available with python. It will return you a float number that will be rounded to the decimal places which are given as input.
If the decimal places to be rounded are not specified, it is considered as 0, and it will round to the nearest integer.
In this Python Tutorial, you will learn:
Syntax:
Parameters
Description
The round() method takes two argument
The second argument is optional and defaults to 0 when not specified, and in such case, it will round to the nearest integer, and the return type will also be an integer.
When the decimal places, i.e. the second argument, is present, it will round to the number of places given. The return type will be a float.
If the number after the decimal place given
How much Impact can Rounding Have? (Rounding vs Truncation)
The best example to show the impact of rounding is for the stock exchange market. In the past i.e in the year 1982, the Vancouver Stock Exchange (VSE): used to truncate the stock values to three decimal places on each trade.
It was done almost 3000 times every day. The accumulated truncations lead to a loss of around 25 points per month.
An example of truncating the values versus rounding is shown below.
Consider the floating-point numbers generated below as stock values. Right now I am generating it for a range of
1,000,000 seconds between 0.01 and 0.05.
Examples:
To show the impact of rounding, I have written a small piece of code wherein at first, you need to use the numbers up to only 3 decimal places, i.e. truncating the number after 3 decimal places.
I have the original total value, the total coming from truncated values and the difference between original and truncated value.
On the same set of numbers, I have been using round() method up to 3 decimal places and calculating the sum and the difference between the original value and the rounded value.
Here are the example and the output
Example 1
Output:
The difference between original and after truncating is 499.9016193868665, and from round, it is 0.04661938686695066
The difference seems to be very big, and the example shows how to round() method helps in calculating close to accuracy.
Example: Rounding Float Numbers
In this program, we will see how rounding words on floating numbers
Example: Rounding Integer Values
If you happen to use round() on an integer value, it will just return you the number back without any changes.
Example: Rounding on Negative Numbers
Let us see few examples of how rounding works on negative numbers
Example: Round Numpy Arrays
How to round numpy arrays in python?
To solve this, we can make use of numpy module and use numpy.round() or numpy.around() method, as shown in the example below.
Using numpy.round()
We can also use numpy.around(), which gives you the same result as shown in the example below.
Example: Decimal Module
In addition to the round() function, python has a decimal module that helps in handling decimal numbers more accurately.
The Decimal module comes with rounding types, as shown below :
In decimal, the quantize() method helps to round to a fixed number of decimal places, and you can specify the rounding to be used, as shown in the example below.
Round float to x decimals?
Is there a way to round a python float to x decimals? For example:
5 Answers 5
Trending sort
Trending sort is based off of the default sorting method — by highest score — but it boosts votes that have happened recently, helping to surface more up-to-date answers.
It falls back to sorting by highest score if no posts are trending.
Switch to Trending sort
I feel compelled to provide a counterpoint to Ashwini Chaudhary’s answer. Despite appearances, the two-argument form of the round function does not round a Python float to a given number of decimal places, and it’s often not the solution you want, even when you think it is. Let me explain.
The ability to round a (Python) float to some number of decimal places is something that’s frequently requested, but turns out to be rarely what’s actually needed. The beguilingly simple answer round(x, number_of_places) is something of an attractive nuisance: it looks as though it does what you want, but thanks to the fact that Python floats are stored internally in binary, it’s doing something rather subtler. Consider the following example:
Finally, as part of Python’s read-eval-print loop (REPL), the floating-point value is displayed (in decimal). That involves converting the binary value back to a decimal string, getting 52.1 as the final output.
In Python 2.7 and later, we have the pleasant situation that the two conversions in step 3 and 4 cancel each other out. That’s due to Python’s choice of repr implementation, which produces the shortest decimal value guaranteed to round correctly to the actual float. One consequence of that choice is that if you start with any (not too large, not too small) decimal literal with 15 or fewer significant digits then the corresponding float will be displayed showing those exact same digits:
Unfortunately, this furthers the illusion that Python is storing values in decimal. Not so in Python 2.6, though! Here’s the original example executed in Python 2.6:
Short version: if you’re using two-argument round, and you’re expecting predictable behaviour from a binary approximation to a decimal round of a binary approximation to a decimal halfway case, you’re asking for trouble.
So enough with the «two-argument round is bad» argument. What should you be using instead? There are a few possibilities, depending on what you’re trying to do.
If you’re rounding for display purposes, then you don’t want a float result at all; you want a string. In that case the answer is to use string formatting:
Even then, one has to be aware of the internal binary representation in order not to be surprised by the behaviour of apparent decimal halfway cases.
If you’re operating in a context where it matters which direction decimal halfway cases are rounded (for example, in some financial contexts), you might want to represent your numbers using the Decimal type. Doing a decimal round on the Decimal type makes a lot more sense than on a binary type (equally, rounding to a fixed number of binary places makes perfect sense on a binary type). Moreover, the decimal module gives you better control of the rounding mode. In Python 3, round does the job directly. In Python 2, you need the quantize method.
How to Round Numbers in Python
Table of Contents
It’s the era of big data, and every day more and more business are trying to leverage their data to make informed decisions. Many businesses are turning to Python’s powerful data science ecosystem to analyze their data, as evidenced by Python’s rising popularity in the data science realm.
One thing every data science practitioner must keep in mind is how a dataset may be biased. Drawing conclusions from biased data can lead to costly mistakes.
There are many ways bias can creep into a dataset. If you’ve studied some statistics, you’re probably familiar with terms like reporting bias, selection bias and sampling bias. There is another type of bias that plays an important role when you are dealing with numeric data: rounding bias.
In this article, you will learn:
Take the Quiz: Test your knowledge with our interactive “Rounding Numbers in Python” quiz. Upon completion you will receive a score so you can track your learning progress over time:
This article is not a treatise on numeric precision in computing, although we will touch briefly on the subject. Only a familiarity with the fundamentals of Python is necessary, and the math involved here should feel comfortable to anyone familiar with the equivalent of high school algebra.
Let’s start by looking at Python’s built-in rounding mechanism.
Python’s Built-in round() Function
The way most people are taught to round a number goes something like this:
Finally, shift the decimal point back p places by dividing m by 10ᵖ.
Now open up an interpreter session and round 2.5 to the nearest whole number using Python’s built-in round() function:
In this article, you’ll learn that there are more ways to round a number than you might expect, each with unique advantages and disadvantages. round() behaves according to a particular rounding strategy—which may or may not be the one you need for a given situation.
You might be wondering, “Can the way I round numbers really have that much of an impact?” Let’s take a look at just how extreme the effects of rounding can be.
How Much Impact Can Rounding Have?
The value of a stock depends on supply and demand. The more people there are who want to buy a stock, the more value that stock has, and vice versa. In high volume stock markets, the value of a particular stock can fluctuate on a second-by-second basis.
You don’t want to keep track of your value to the fifth or sixth decimal place, so you decide to chop everything off after the third decimal place. In rounding jargon, this is called truncating the number to the third decimal place. There’s some error to be expected here, but by keeping three decimal places, this error couldn’t be substantial. Right?
To run our experiment using Python, let’s start by writing a truncate() function that truncates a number to three decimal places:
Next, let’s define the initial parameters of the simulation. You’ll need two variables: one to keep track of the actual value of your stocks after the simulation is complete and one for the value of your stocks after you’ve been truncating to three decimal places at each step.
Start by initializing these variables to 100 :
Note: In the above example, the random.seed() function is used to seed the pseudo-random number generator so that you can reproduce the output shown here.
To learn more about randomness in Python, check out Real Python’s Generating Random Data in Python (Guide).
Ignoring for the moment that round() doesn’t behave quite as you expect, let’s try re-running the simulation. We’ll use round() this time to round to three decimal places at each step, and seed() the simulation again to get the same results as before:
What a difference!
Shocking as it may seem, this exact error caused quite a stir in the early 1980s when the system designed for recording the value of the Vancouver Stock Exchange truncated the overall index value to three decimal places instead of rounding. Rounding errors have swayed elections and even resulted in the loss of life.
How you round numbers is important, and as a responsible developer and software designer, you need to know what the common issues are and how to deal with them. Let’s dive in and investigate what the different rounding methods are and how you can implement each one in pure Python.
A Menagerie of Methods
There are a plethora of rounding strategies, each with advantages and disadvantages. In this section, you’ll learn about some of the most common techniques, and how they can influence your data.
Truncation
The simplest, albeit crudest, method for rounding a number is to truncate the number to a given number of digits. When you truncate a number, you replace each digit after a given position with 0. Here are some examples:
| Value | Truncated To | Result |
|---|---|---|
| 12.345 | Tens place | 10 |
| 12.345 | Ones place | 12 |
| 12.345 | Tenths place | 12.3 |
| 12.345 | Hundredths place | 12.34 |
You’ve already seen one way to implement this in the truncate() function from the How Much Impact Can Rounding Have? section. In that function, the input number was truncated to three decimal places by:
You can generalize this process by replacing 1000 with the number 10ᵖ ( 10 raised to the pth power), where p is the number of decimal places to truncate to:
The truncate() function works well for both positive and negative numbers:
You can even pass a negative number to decimals to truncate to digits to the left of the decimal point:
When you truncate a positive number, you are rounding it down. Likewise, truncating a negative number rounds that number up. In a sense, truncation is a combination of rounding methods depending on the sign of the number you are rounding.
Let’s take a look at each of these rounding methods individually, starting with rounding up.
Rounding Up
The second rounding strategy we’ll look at is called “rounding up.” This strategy always rounds a number up to a specified number of digits. The following table summarizes this strategy:
| Value | Round Up To | Result |
|---|---|---|
| 12.345 | Tens place | 20 |
| 12.345 | Ones place | 13 |
| 12.345 | Tenths place | 12.4 |
| 12.345 | Hundredths place | 12.35 |
To implement the “rounding up” strategy in Python, we’ll use the ceil() function from the math module.
The ceil() function gets its name from the term “ceiling,” which is used in mathematics to describe the nearest integer that is greater than or equal to a given number.
In Python, math.ceil() implements the ceiling function and always returns the nearest integer that is greater than or equal to its input:
Let’s write a function called round_up() that implements the “rounding up” strategy:
This pattern of shifting the decimal point, applying some rounding method to round to an integer, and then shifting the decimal point back will come up over and over again as we investigate more rounding methods. This is, after all, the mental algorithm we humans use to round numbers by hand.
Let’s look at how well round_up() works for different inputs:
Take a guess at what round_up(-1.5) returns:
Let’s establish some terminology. For our purposes, we’ll use the terms “round up” and “round down” according to the following diagram:

Rounding up always rounds a number to the right on the number line, and rounding down always rounds a number to the left on the number line.
Rounding Down
The counterpart to “rounding up” is the “rounding down” strategy, which always rounds a number down to a specified number of digits. Here are some examples illustrating this strategy:
| Value | Rounded Down To | Result |
|---|---|---|
| 12.345 | Tens place | 10 |
| 12.345 | Ones place | 12 |
| 12.345 | Tenths place | 12.3 |
| 12.345 | Hundredths place | 12.34 |
Lucky for us, the math module has a floor() function that returns the floor of its input:
Here’s the definition of round_down() :
You can test round_down() on a few different values:
The effects of round_up() and round_down() can be pretty extreme. By rounding the numbers in a large dataset up or down, you could potentially remove a ton of precision and drastically alter computations made from the data.
Before we discuss any more rounding strategies, let’s stop and take a moment to talk about how rounding can make your data biased.
Interlude: Rounding Bias
There is one important difference between truncate() and round_up() and round_down() that highlights an important aspect of rounding: symmetry around zero.
The concept of symmetry introduces the notion of rounding bias, which describes how rounding affects numeric data in a dataset.
The “rounding up” strategy has a round towards positive infinity bias, because the value is always rounded up in the direction of positive infinity. Likewise, the “rounding down” strategy has a round towards negative infinity bias.
The “truncation” strategy exhibits a round towards negative infinity bias on positive values and a round towards positive infinity for negative values. Rounding functions with this behavior are said to have a round towards zero bias, in general.
Let’s see how this works in practice. Consider the following list of floats:
Let’s compute the mean value of the values in data using the statistics.mean() function:
This example does not imply that you should always truncate when you need to round individual values while preserving a mean value as closely as possible. The data list contains an equal number of positive and negative values. The truncate() function would behave just like round_up() on a list of all positive values, and just like round_down() on a list of all negative values.
What this example does illustrate is the effect rounding bias has on values computed from data that has been rounded. You will need to keep these effects in mind when drawing conclusions from data that has been rounded.
Typically, when rounding, you are interested in rounding to the nearest number with some specified precision, instead of just rounding everything up or down.
The way that most people are taught break ties is by rounding to the greater of the two possible numbers.
Rounding Half Up
The “rounding half up” strategy rounds every number to the nearest number with the specified precision, and breaks ties by rounding up. Here are some examples:
| Value | Round Half Up To | Result |
|---|---|---|
| 13.825 | Tens place | 10 |
| 13.825 | Ones place | 14 |
| 13.825 | Tenths place | 13.8 |
| 13.825 | Hundredths place | 13.83 |
If the digit in the first decimal place of the shifted value is less than five, then adding 0.5 won’t change the integer part of the shifted value, so the floor is equal to the integer part.
Here’s what this looks like in Python:
Let’s test round_half_up() on a couple of values to see that it works:
Great! You can now finally get that result that the built-in round() function denied to you:
Is there a bug in the round_half_up() function?
Aside: In a Python interpreter session, type the following:
Seeing this for the first time can be pretty shocking, but this is a classic example of floating-point representation error. It has nothing to do with Python. The error has to do with how machines store floating-point numbers in memory.
Most modern computers store floating-point numbers as binary decimals with 53-bit precision. Only numbers that have finite binary decimal representations that can be expressed in 53 bits are stored as an exact value. Not every number has a finite binary decimal representation.
A value with an infinite binary representation is rounded to an approximate value to be stored in memory. The method that most machines use to round is determined according to the IEEE-754 standard, which specifies rounding to the nearest representable binary fraction.
The Python docs have a section called Floating Point Arithmetic: Issues and Limitations which has this to say about the number 0.1:
That is more digits than most people find useful, so Python keeps the number of digits manageable by displaying a rounded value instead
For a more in-depth treatise on floating-point arithmetic, check out David Goldberg’s article What Every Computer Scientist Should Know About Floating-Point Arithmetic, originally published in the journal ACM Computing Surveys, Vol. 23, No. 1, March 1991.
Floating-point numbers do not have exact precision, and therefore should not be used in situations where precision is paramount. For applications where the exact precision is necessary, you can use the Decimal class from Python’s decimal module. You’ll learn more about the Decimal class below.
If you have determined that Python’s standard float class is sufficient for your application, some occasional errors in round_half_up() due to floating-point representation error shouldn’t be a concern.
Now that you’ve gotten a taste of how machines round numbers in memory, let’s continue our discussion on rounding strategies by looking at another way to break a tie.
Rounding Half Down
The “rounding half down” strategy rounds to the nearest number with the desired precision, just like the “rounding half up” method, except that it breaks ties by rounding to the lesser of the two numbers. Here are some examples:
| Value | Round Half Down To | Result |
|---|---|---|
| 13.825 | Tens place | 10 |
| 13.825 | Ones place | 14 |
| 13.825 | Tenths place | 13.8 |
| 13.825 | Hundredths place | 13.82 |
You can implement the “rounding half down” strategy in Python by replacing math.floor() in the round_half_up() function with math.ceil() and subtracting 0.5 instead of adding:
Let’s check round_half_down() against a few test cases:
Both round_half_up() and round_half_down() have no bias in general. However, rounding data with lots of ties does introduce a bias. For an extreme example, consider the following list of numbers:
Let’s compute the mean of these numbers:
Next, compute the mean on the data after rounding to one decimal place with round_half_up() and round_half_down() :
Every number in data is a tie with respect to rounding to one decimal place. The round_half_up() function introduces a round towards positive infinity bias, and round_half_down() introduces a round towards negative infinity bias.
The remaining rounding strategies we’ll discuss all attempt to mitigate these biases in different ways.
Rounding Half Away From Zero
If you examine round_half_up() and round_half_down() closely, you’ll notice that neither of these functions is symmetric around zero:
One way to introduce symmetry is to always round a tie away from zero. The following table illustrates how this works:
| Value | Round Half Away From Zero To | Result |
|---|---|---|
| 15.25 | Tens place | 20 |
| 15.25 | Ones place | 15 |
| 15.25 | Tenths place | 15.3 |
| -15.25 | Tens place | -20 |
| -15.25 | Ones place | -15 |
| -15.25 | Tenths place | -15.3 |
After rounding according to one of the above four rules, you then shift the decimal place back to the left.
That’s easy enough, but there’s actually a simpler way!
math.copysign() takes two numbers a and b and returns a with the sign of b :
Checking round_half_away_from_zero() on a few different values shows that the function behaves as expected:
The round_half_away_from_zero() function rounds numbers the way most people tend to round numbers in everyday life. Besides being the most familiar rounding function you’ve seen so far, round_half_away_from_zero() also eliminates rounding bias well in datasets that have an equal number of positive and negative ties.
Let’s check how well round_half_away_from_zero() mitigates rounding bias in the example from the previous section:
However, round_half_away_from_zero() will exhibit a rounding bias when you round every number in datasets with only positive ties, only negative ties, or more ties of one sign than the other. Bias is only mitigated well if there are a similar number of positive and negative ties in the dataset.
How do you handle situations where the number of positive and negative ties are drastically different? The answer to this question brings us full circle to the function that deceived us at the beginning of this article: Python’s built-in round() function.
Rounding Half To Even
One way to mitigate rounding bias when rounding values in a dataset is to round ties to the nearest even number at the desired precision. Here are some examples of how to do that:
| Value | Round Half To Even To | Result |
|---|---|---|
| 15.255 | Tens place | 20 |
| 15.255 | Ones place | 15 |
| 15.255 | Tenths place | 15.3 |
| 15.255 | Hundredths place | 15.26 |
The “rounding half to even strategy” is the strategy used by Python’s built-in round() function and is the default rounding rule in the IEEE-754 standard. This strategy works under the assumption that the probabilities of a tie in a dataset being rounded down or rounded up are equal. In practice, this is usually the case.
To prove to yourself that round() really does round to even, try it on a few different values:
The round() function is nearly free from bias, but it isn’t perfect. For example, rounding bias can still be introduced if the majority of the ties in your dataset round up to even instead of rounding down. Strategies that mitigate bias even better than “rounding half to even” do exist, but they are somewhat obscure and only necessary in extreme circumstances.
Finally, round() suffers from the same hiccups that you saw in round_half_up() thanks to floating-point representation error:
You shouldn’t be concerned with these occasional errors if floating-point precision is sufficient for your application.
When precision is paramount, you should use Python’s Decimal class.
The Decimal Class
Python’s decimal module is one of those “batteries-included” features of the language that you might not be aware of if you’re new to Python. The guiding principle of the decimal module can be found in the documentation:
Decimal “is based on a floating-point model which was designed with people in mind, and necessarily has a paramount guiding principle – computers must provide an arithmetic that works in the same way as the arithmetic that people learn at school.” – excerpt from the decimal arithmetic specification. (Source)
The benefits of the decimal module include:
Let’s explore how rounding works in the decimal module. Start by typing the following into a Python REPL:
decimal.getcontext() returns a Context object representing the default context of the decimal module. The context includes the default precision and the default rounding strategy, among other things.
Let’s declare a number using the decimal module’s Decimal class. To do so, create a new Decimal instance by passing a string containing the desired value:
Note: It is possible to create a Decimal instance from a floating-point number, but doing so introduces floating-point representation error right off the bat. For example, check out what happens when you create a Decimal instance from the floating-point number 0.1 :
In order to maintain exact precision, you must create Decimal instances from strings containing the decimal numbers you need.
Just for fun, let’s test the assertion that Decimal maintains exact decimal representation:
Ahhh. That’s satisfying, isn’t it?
Another benefit of the decimal module is that rounding after performing arithmetic is taken care of automatically, and significant digits are preserved. To see this in action, let’s change the default precision from twenty-eight digits to two, and then add the numbers 1.23 and 2.32 :
To change the default rounding strategy, you can set the decimal.getcontect().rounding property to any one of several flags. The following table summarizes these flags and which rounding strategy they implement:
| Flag | Rounding Strategy |
|---|---|
| decimal.ROUND_CEILING | Rounding up |
| decimal.ROUND_FLOOR | Rounding down |
| decimal.ROUND_DOWN | Truncation |
| decimal.ROUND_UP | Rounding away from zero |
| decimal.ROUND_HALF_UP | Rounding half away from zero |
| decimal.ROUND_HALF_DOWN | Rounding half towards zero |
| decimal.ROUND_HALF_EVEN | Rounding half to even |
| decimal.ROUND_05UP | Rounding up and rounding towards zero |
The first thing to notice is that the naming scheme used by the decimal module differs from what we agreed to earlier in the article. For example, decimal.ROUND_UP implements the “rounding away from zero” strategy, which actually rounds negative numbers down.
Secondly, some of the rounding strategies mentioned in the table may look unfamiliar since we haven’t discussed them. You’ve already seen how decimal.ROUND_HALF_EVEN works, so let’s take a look at each of the others in action.
The decimal.ROUND_CEILING strategy works just like the round_up() function we defined earlier:
Notice that the results of decimal.ROUND_CEILING are not symmetric around zero.
The decimal.ROUND_FLOOR strategy works just like our round_down() function:
The decimal.ROUND_DOWN and decimal.ROUND_UP strategies have somewhat deceptive names. Both ROUND_DOWN and ROUND_UP are symmetric around zero:
The decimal.ROUND_DOWN strategy rounds numbers towards zero, just like the truncate() function. On the other hand, decimal.ROUND_UP rounds everything away from zero. This is a clear break from the terminology we agreed to earlier in the article, so keep that in mind when you are working with the decimal module.
There are three strategies in the decimal module that allow for more nuanced rounding. The decimal.ROUND_HALF_UP method rounds everything to the nearest number and breaks ties by rounding away from zero:
There is also a decimal.ROUND_HALF_DOWN strategy that breaks ties by rounding towards zero:
The final rounding strategy available in the decimal module is very different from anything we have seen so far:
In this section, we have only focused on the rounding aspects of the decimal module. There are a large number of other features that make decimal an excellent choice for applications where the standard floating-point precision is inadequate, such as banking and some problems in scientific computing.
Next, let’s turn our attention to two staples of Python’s scientific computing and data science stacks: NumPy and Pandas.
Rounding NumPy Arrays
Let’s generate some data by creating a 3×4 NumPy array of pseudo-random numbers:
Note: You’ll need to pip3 install numpy before typing the above code into your REPL if you don’t already have NumPy in your environment. If you installed Python with Anaconda, you’re already set!
If you haven’t used NumPy before, you can get a quick introduction in the Getting Into Shape section of Brad Solomon’s Look Ma, No For-Loops: Array Programming With NumPy here at Real Python.
For more information on NumPy’s random module, check out the PRNG’s for Arrays section of Brad’s Generating Random Data in Python (Guide).
To round all of the values in the data array, you can pass data as the argument to the np.around() function. The desired number of decimal places is set with the decimals keyword argument. The round half to even strategy is used, just like Python’s built-in round() function.
For example, the following rounds all of the values in data to three decimal places:
np.around() is at the mercy of floating-point representation error, just like round() is.
If you need to round the data in your array to integers, NumPy offers several options:
The np.ceil() function rounds every value in the array to the nearest integer greater than or equal to the original value:
Hey, we discovered a new number! Negative zero!
Actually, the IEEE-754 standard requires the implementation of both a positive and negative zero. What possible use is there for something like this? Wikipedia knows the answer:
Informally, one may use the notation “ −0 ” for a negative value that was rounded to zero. This notation may be useful when a negative sign is significant; for example, when tabulating Celsius temperatures, where a negative sign means below freezing. (Source)
To round every value down to the nearest integer, use np.floor() :
You can also truncate each value to its integer component with np.trunc() :
Finally, to round to the nearest integer using the “rounding half to even” strategy, use np.rint() :
Thanks to NumPy’s vectorized operations, this works just as you expect:
Now that you’re a NumPy rounding master, let’s take a look at Python’s other data science heavy-weight: the Pandas library.
Rounding Pandas Series and DataFrame
The Pandas library has become a staple for data scientists and data analysts who work in Python. In the words of Real Python’s own Joe Wyndham:
Pandas is a game-changer for data science and analytics, particularly if you came to Python because you were searching for something more powerful than Excel and VBA. (Source)
Note: Before you continue, you’ll need to pip3 install pandas if you don’t already have it in your environment. As was the case for NumPy, if you installed Python with Anaconda, you should be ready to go!
The modified round_half_up() function from the previous section will also work here:
Congratulations, you’re well on your way to rounding mastery! You now know that there are more ways to round a number than there are taco combinations. (Well… maybe not!) You can implement numerous rounding strategies in pure Python, and you have sharpened your skills on rounding NumPy arrays and Pandas Series and DataFrame objects.
There’s just one more step: knowing when to apply the right strategy.
Applications and Best Practices
The last stretch on your road to rounding virtuosity is understanding when to apply your newfound knowledge. In this section, you’ll learn some best practices to make sure you round your numbers the right way.
Store More and Round Late
When you deal with large sets of data, storage can be an issue. In most relational databases, each column in a table is designed to store a specific data type, and numeric data types are often assigned precision to help conserve memory.
For example, a temperature sensor may report the temperature in a long-running industrial oven every ten seconds accurate to eight decimal places. The readings from this are used to detect abnormal fluctuations in temperature that could indicate the failure of a heating element or some other component. So, there might be a Python script running that compares each incoming reading to the last to check for large fluctuations.
For this calculation, you only need three decimal places of precision. But you know from the incident at the Vancouver Stock Exchange that removing too much precision can drastically affect your calculation.
If you have the space available, you should store the data at full precision. If storage is an issue, a good rule of thumb is to store at least two or three more decimal places of precision than you need for your calculation.
Finally, when you compute the daily average temperature, you should calculate it to the full precision available and round the final answer.
Obey Local Currency Regulations
Situations like this can also arise when you are converting one currency to another. In 1999, the European Commission on Economical and Financial Affairs codified the use of the “rounding half away from zero” strategy when converting currencies to the Euro, but other currencies may have adopted different regulations.
How situations like this are handled is typically determined by a country’s government. You can find a list of rounding methods used by various countries on Wikipedia.
If you are designing software for calculating currencies, you should always check the local laws and regulations in your users’ locations.
When In Doubt, Round Ties To Even
When you are rounding numbers in large datasets that are used in complex computations, the primary concern is limiting the growth of the error due to rounding.
Of all the methods we’ve discussed in this article, the “rounding half to even” strategy minimizes rounding bias the best. Fortunately, Python, NumPy, and Pandas all default to this strategy, so by using the built-in rounding functions you’re already well protected!
Summary
Whew! What a journey this has been!
In this article, you learned that:
There are various rounding strategies, which you now know how to implement in pure Python.
Every rounding strategy inherently introduces a rounding bias, and the “rounding half to even” strategy mitigates this bias well, most of the time.
The way in which computers store floating-point numbers in memory naturally introduces a subtle rounding error, but you learned how to work around this with the decimal module in Python’s standard library.
You can round NumPy arrays and Pandas Series and DataFrame objects.
There are best practices for rounding with real-world data.
Take the Quiz: Test your knowledge with our interactive “Rounding Numbers in Python” quiz. Upon completion you will receive a score so you can track your learning progress over time:
If you are interested in learning more and digging into the nitty-gritty details of everything we’ve covered, the links below should keep you busy for quite a while.
At the very least, if you’ve enjoyed this article and learned something new from it, pass it on to a friend or team member! Be sure to share your thoughts with us in the comments. We’d love to hear some of your own rounding-related battle stories!
Additional Resources
Rounding strategies and bias:
Floating-point and decimal specifications:
Interesting Reads:
Get a short & sweet Python Trick delivered to your inbox every couple of days. No spam ever. Unsubscribe any time. Curated by the Real Python team.
About David Amos

David is a writer, programmer, and mathematician passionate about exploring mathematics through code.
Each tutorial at Real Python is created by a team of developers so that it meets our high quality standards. The team members who worked on this tutorial are:
Master Real-World Python Skills With Unlimited Access to Real Python
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
Master Real-World Python Skills
With Unlimited Access to Real Python
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
What Do You Think?
What’s your #1 takeaway or favorite thing you learned? How are you going to put your newfound skills to use? Leave a comment below and let us know.
Commenting Tips: The most useful comments are those written with the goal of learning from or helping out other students. Get tips for asking good questions and get answers to common questions in our support portal. Looking for a real-time conversation? Visit the Real Python Community Chat or join the next “Office Hours” Live Q&A Session. Happy Pythoning!
How to Round Floats in Python : Know 3 Methods
When you do any calculation using the float value and print its output then you will see the number of digits after the decimal is very long. Thus it bothered someone who does not want the long digits. They want to round float to some digits. In this entire tutorial of ” How to”, you will know how to round floats in python using various methods.
How Floats Look without Rounding
Let’s say I have a float variable and an integer variable. When I perform calculations like multiplication and print its output then I will get the output as below.
Output
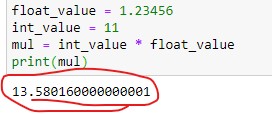
You can see the number of digits after the decimal point is very large. That’s why we prefer rounding of digits. In the next section, you will know all the methods to Round Floats in Python.
How to round off float in python: Methods
Method 1: Round Float value using the round() method
There is a function in python that allows you to round any float value. And it is round(). The syntax of it is below.
How to round float to 2 decimal places in python
Let’s say I want to round the above multiplication results to up to 2 digits, then I will use the following code.
Output 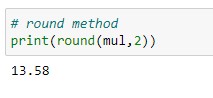
In the same way, just use 3 to round the float value to 3 digits.
Method 2 : Using str.format()
The second method to round float value is using the python str.format() method. It has two parts one is a string and the other, format() method. The syntax for using it is below.
If I apply it to the same multiplication results then I will get the output as below.
Output 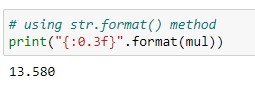
Method 3: Round Float Value using NumPy
The last method to round float value in python is using NumPy. Numpy is a python module that has a function np.round() that is the same method as python round(). But in numpy.round() all values are treated as a numpy array. Using the same example, I will use the numpy.round() method on the multiplication results.
Output
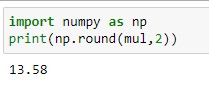
Conclusion
Rounding the float value is a must if you want to find the approximate results of any calculation. These are the methods I have compiled for you to round any float value. If you want to add any other methods then you can contact us. And if you have other queries then you can directly message us at the Offical Data Science Learner Facebook Page.
Join our list
Subscribe to our mailing list and get interesting stuff and updates to your email inbox.
We respect your privacy and take protecting it seriously
Thank you for signup. A Confirmation Email has been sent to your Email Address.
How to round to whole numbers in Python?
When our Python program works with numerical values, every so often we have turn values with a fractional component into whole (integer) numbers. But how to do so? And what options does Python have? Let’s find out together.
IN THIS ARTICLE:
# Round numerical values up and down in Python
When we round values, we go from a numerical value with decimal places to a whole number. With this process we do lose some precision, but the rounded value is often much easier to read and interpret.
Python has three ways to turn a floating-point value into a whole (integer) number:
If you just want a string or script output with a whole number, then a Python format string can perform that task too. That way you also don’t lose precision in the original value.
Let’s see how these three approaches work.
round() function'»># Round values up and down: Python’s round() function
To round floating-point values up and down we use Python’s round() function (Lutz, 2013; Python Docs, n.d. a). There are two ways to use this function. The first option is to round values to a certain number of decimals. The other option turns a floating-point value into a whole number.
To do that latter, we call round() with one argument: the value to turn into an integer. For example:
# Example: round Python numbers to the nearest full integer
To see how the round() function works in practice, let’s consider the following mini-program:
Here we first make five variables with floating-point values. Some have a lot of decimal places and others just a few.
Next we output the results with the print() function. For each variable we display the original value (e.g., valueA ) and its rounded result ( roundA ). With the ljust() string method we justify that first value to the left. That aligns the values for a prettier output.
Here’s how the rounded values look:
math.floor() function'»># Round down to the next integer: Python’s math.floor() function
The math.floor() function returns the floor value of its argument, which is the nearest integer less than or equal to that argument’s value (Python Docs, n.d. b).
Here’s a quick example of the math.floor() function:
math.floor() only accepts one argument: the value to round down. With a small custom function we can also round down to a number of decimal places. See round down to a specific decimal amount for more.
# Example: round values down to the next full integer
To explore how the math.floor() function works in practice, let’s examine the following Python program:
Next we round those values down. For that we call the math.floor() function on each variable. We store the outcome in new variables ( roundA through roundE ).
The program’s third part outputs the variables with Python’s print() function. Here each print() statement displays the original value and its rounded down version. Here’s how that looks:
math.ceil() function'»># Round up to the next integer: Python’s math.ceil() function
The math.ceil() function returns the ceiling of its argument, which is the nearest integer greater than or equal to that argument’s value (Python Docs, n.d. b).
Here’s a quick example of math.ceil() :
Python’s math.ceil() function always rounds up to a full integer. But with a small custom function we can also round up to a number of decimal places. See round Python values to decimal places for how.
# Example: round Python values up to whole numbers
Let’s see how math.ceil() works in practice. This example program rounds several floating-point values up to a whole number:
The third code segment has the print() function output both the original and rounded value. Here’s what that displays:
# Round all values in a Python list or array
Of course there are also situations where we have a bunch of values to round, rather than a single value. There are two main ways to do that: with a list comprehension or for loop. Let’s see.
# Round Python values with a list comprehension
When we have a sequence of floating-point values, one way to round them is with a list comprehension. That requires just a bit of code and runs efficiently.
Here’s a mini-program that does just that:
To round those values to whole numbers we make three list comprehensions. The first one executes round() for each list value. The other two execute math.ceil() and math.floor() functions on the list values.
The last part of the program outputs the original list and the three rounded ones. Here’s how that looks:
In the above example we kept the original list. If you don’t need to retain those values, you can also overwrite the original list with rounded values. Here’s how a list comprehension does that:
for loop'»># Round all values with Python’s for loop
Of course we can also round list or array values with a regular for loop. This requires a bit more code than a list comprehension, but makes it easier to perform additional operations on each element. Plus a for loop is easier to read in complex situations.
Here’s how a Python program rounds values inside a for loop:
To fill those lists we make a Python for loop. This loop goes through all elements in the values list. During each loop cycle the number variable holds a single element from that list.
The program ends with several print() statements. That displays the original list and its rounded derivatives. Here’s what that output looks like:
By the way, you don’t have to make a new list when you round values. If you’re fine with losing the original data, you can also overwrite the existing list. Doing so is easy when you combine a for loop with the enumerate() function:
# Summary
The math.floor() function, on the other hand, always rounds down to the nearest full integer. math.ceil() does the opposite. That function always rounds up to a whole number.
All three functions work in the same way: provide the function with one argument, which is the floating-point value to round.
References
Lutz, M. (2013). Learning Python (5th Edition). Sebastopol, CA: O’Reilly Media.
Python.org (n.d. a). Built-in Functions. Retrieved on November 8, 2019, from https://docs.python.org/3/library/functions.html
Python.org (n.d. b). math — Mathematical functions. Retrieved on October 22, 2019, from https://docs.python.org/3.8/library/math.html
# Related Python tutorials
A square is a number multiplied by itself. In Python ** and pow() square by raising to the power 2, while * can multiply a value with itself.
Python’s abs() returns absolute values, also for different bases than 10 (binary, octal, hexadecimal). For complex numbers it gives the magnitude.
An absolute value is a number’s non-negative value. Python code gets those with the abs() function. This article explains how (including lists & arrays).
When we truncate a number, we throw away its fractional value. But with a custom function Python can also truncate to a certain amount of decimal places.
When we truncate numbers, we throw away their fractional part. Our Python program implements that behaviour with the math.trunc() or int() function.
Welcome on Kodify.net! This website aims to help people like you reduce their programming curve. I hope you find the articles helpful with your programming tasks.
Want to know more about me? Check out the about page.
See all TradingView tutorials to learn about a lot of Pine Script features





